




SciPy是一个Python中用于进行科学计算的工具集,它有很多功能,如计算统计学分布、信号处理、计算线性代数方程等。scikit-learn需要使用SciPy来对算法进行执行,其中用得最多的就是SciPy中的sparse()函数。sparse()函数用来生成稀疏矩阵,而稀疏矩阵用来存储那些大部分数值为0的np数组,这种类型的数组在scikit-learn的实际应用中也非常常见。
由于稀疏矩阵中非零元素较少,零元素较多,因此可以采用只存储非零元素的方法来进行压缩存储。对于一个用二维数组 m × n 存储的稀疏矩阵,如果存储每个数组元素需要 L 字节,那么存储整个矩阵需要 m × n × L 字节。但是,这些存储空间的大部分存放的是0元素,从而造成大量的空间浪费。为了节省存储空间,可以只存储其中的非0元素。
另外,对于很多元素为零的稀疏矩阵,仅存储非零元素可使矩阵操作效率更高。也就是稀疏矩阵的计算速度更快,因为只对非零元素进行操作,这是稀疏矩阵的一个突出的优点。
Python不能自动创建稀疏矩阵,所以要用SciPy中特殊的命令来得到稀疏矩阵。下面直接通过代码来展示sparse()函数的用法。
【例2-34】 利用sparse()函数创建稀疏矩阵。
import numpy as np
from scipy import sparse
matrix=np.eye(6)#生成一个6行6列的对角矩阵
#矩阵中对角线上的元素数值为1,其余都是0
sparse_matrix=sparse.csr_matrix(matrix)
#把np数组转换为CSR格式的SciPy稀疏矩阵(SparseMatrix)
#sparse()函数只会存储非0元素
print('对角矩阵:\n{}'.format(matrix))
print("\n sparse存储的矩阵:\n{}".format(sparse_matrix))
运行程序,输出如下。
对角矩阵:
[[1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 1.]]
sparse存储的矩阵:
(0,0) 1.0
(1,1) 1.0
(2,2) 1.0
(3,3) 1.0
(4,4) 1.0
(5,5) 1.0
在以上结果中,(0,0)表示矩阵的左上角,这个点对应的值是1.0,而(1,1)代表矩阵的第2行第2列,这个点对应的数值也是1.0,以此类推,直到右下角的点(5,5)。
SciPy有很多模块,在对数据进行插值时,使用的核心模块是scipy.interpolate。
分段线性插值的基本原理就是把相邻的两个节点连起来,从而实现节点两两之间的线性插值,将这条分段的折线记作 I n ( x i )= y i ,且 I n ( x i )在每个小区间[ x i , x i +1 ]上都是线性函数。
【例2-35】 分段线性插值。

运行程序,效果如图2-1所示。
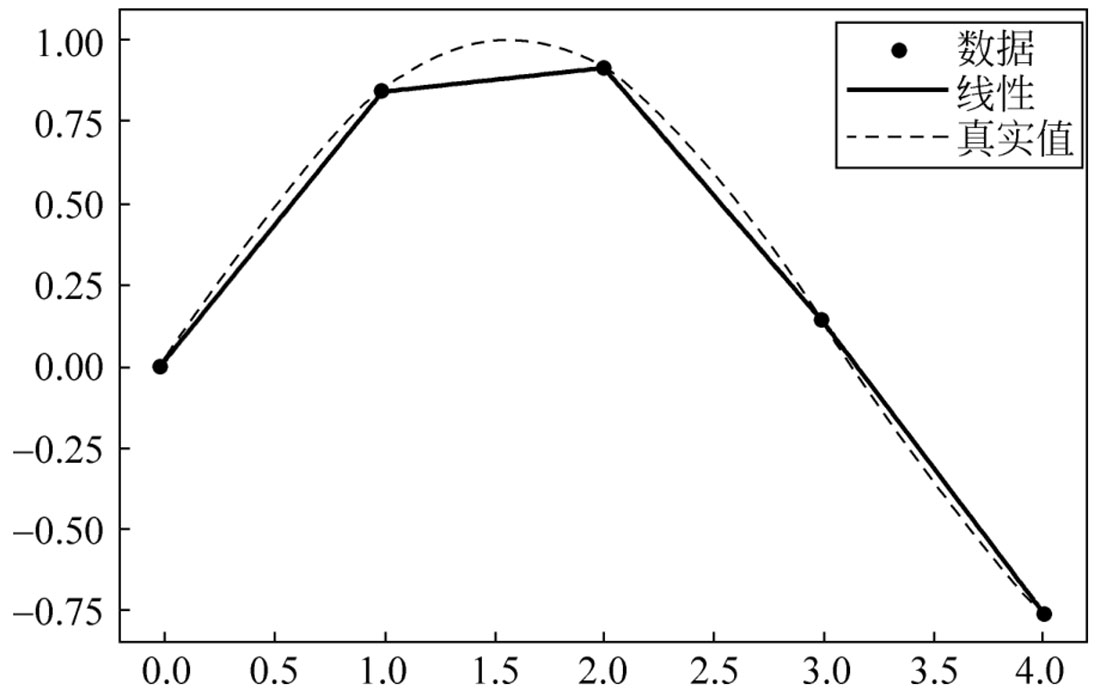
图2-1 分段线性插值
对某个多项式函数有已知的 k +1个点,假设任意两个不同的点都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
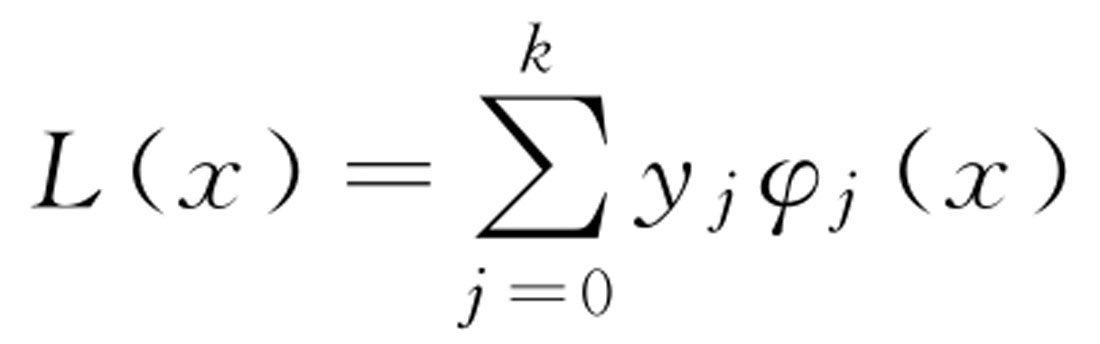
其中,每个 φ j ( x )为拉格朗日基本多项式(或称插值基函数),其表达式为:
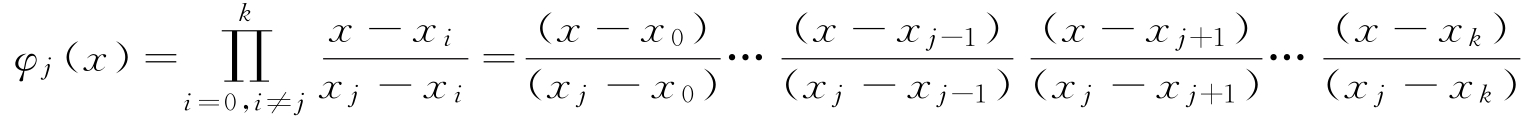
在SciPy中,直接调用lagrange(x,y)这个函数即可实现拉格朗日插值。
【例2-36】 实现拉格朗日插值。
#-*-coding:utf-8-*-
from scipy.interpolate import lagrange
import numpy as np
import matplotlib.pyplot as plt
def interp_lagrange(x,y,xx):
#调用拉格朗日插值,得到插值函数p
p=lagrange(x,y)
yy=p(xx)
plt.plot(x,y,"b * ")
plt.plot(xx,yy,"ro")
plt.show()
if__name__== '__main__':
NUMBER=20
eps=np.random.rand(NUMBER) * 2
#构造样本数据
x=np.linspace(0,20,NUMBER)
y=np.linspace(2,14,NUMBER)+eps
#兴趣点数据
xx=np.linspace(12,15,10)
interp_lagrange(x,y,xx)
运行程序,效果如图2-2所示。
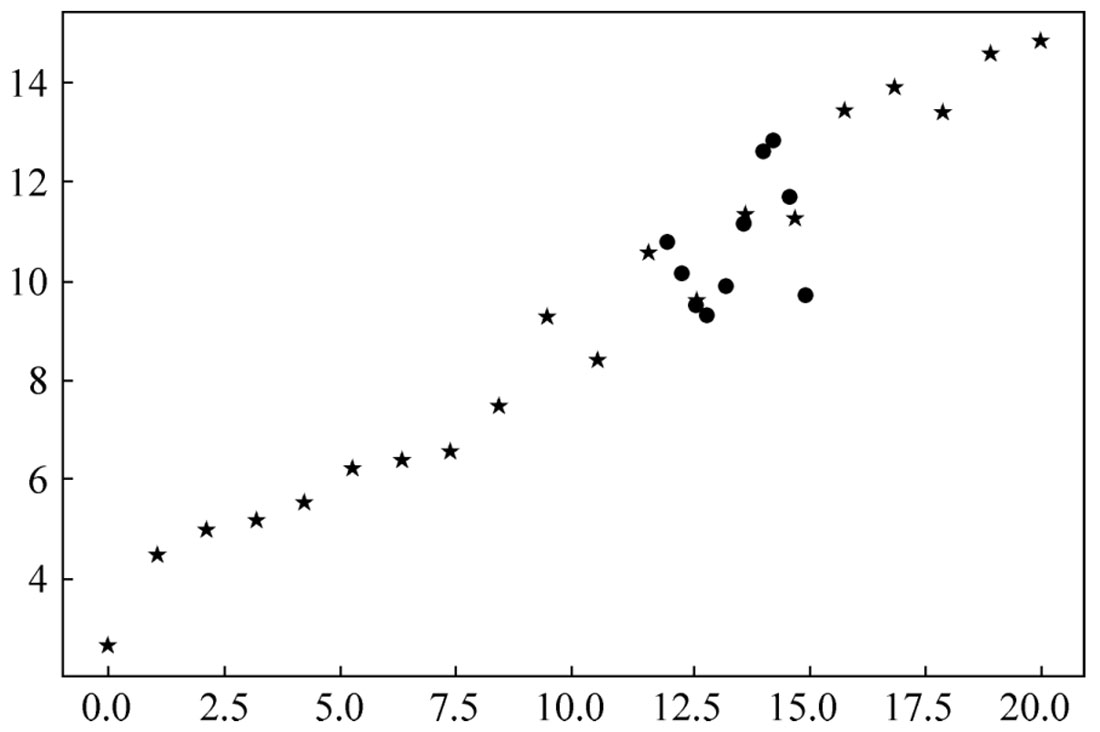
图2-2 拉格朗日插值
样条插值法是一种以可变样条来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的,每个多项式都是由相邻的两个数据点决定的,这样,任意两个相邻的多项式以及它们的导数在连接点处都是连续的。连接点的光滑与连续是样条插值和前边分段多项式插值的主要区别。
【例2-37】 实现样条插值。
import numpy as np
import pylab as pl
from scipy import interpolate
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus']=False#显示负号
def generate_data(begin,end,num):
"""产生x点集"""
x=np.linspace(begin,end,num)
return x
def generate_sin(x):
"""得到sin函数的x对应的y点"""
y=np.sin(x)
return y
def interpolate_linear(x,y):
"""线性插值"""
f_linear= interpolate.interp1d(x,y)
return f_linear
def interpolate_b_spline(x,y,x_new,der=0):
"""B样条曲线插值或者导数,默认der=0"""
tck= interpolate.splrep(x,y)
y_bspline=interpolate.splev(x_new,tck,der=der)
return y_bspline
def test_interpolate():
begin=0
end=2 * np.pi+np.pi/4
pt_x=generate_data(begin=begin,end=end,num=10)
pt_y=generate_sin(pt_x)
interpolate_x=generate_data(begin=begin,end=end,num=100)
f_linear= interpolate_linear(pt_x,pt_y)
y_bspline=interpolate_b_spline(pt_x,pt_y,interpolate_x,der=0)
#一阶导数
y_bspine_derivative= interpolate_b_spline(pt_x,pt_y,interpolate_x,der=1)
pl.plot(pt_x,pt_y,"o",label=u"原始数据")
pl.plot(interpolate_x,f_linear(interpolate_x),label=u"线性")
pl.plot(interpolate_x,y_bspline,label=u"B样条")
pl.plot(interpolate_x,y_bspine_derivative,label=u"B样条函数阶")
pl.legend()
pl.show()
if__name__== '__main__':
test_interpolate()
运行程序,效果如图2-3所示。
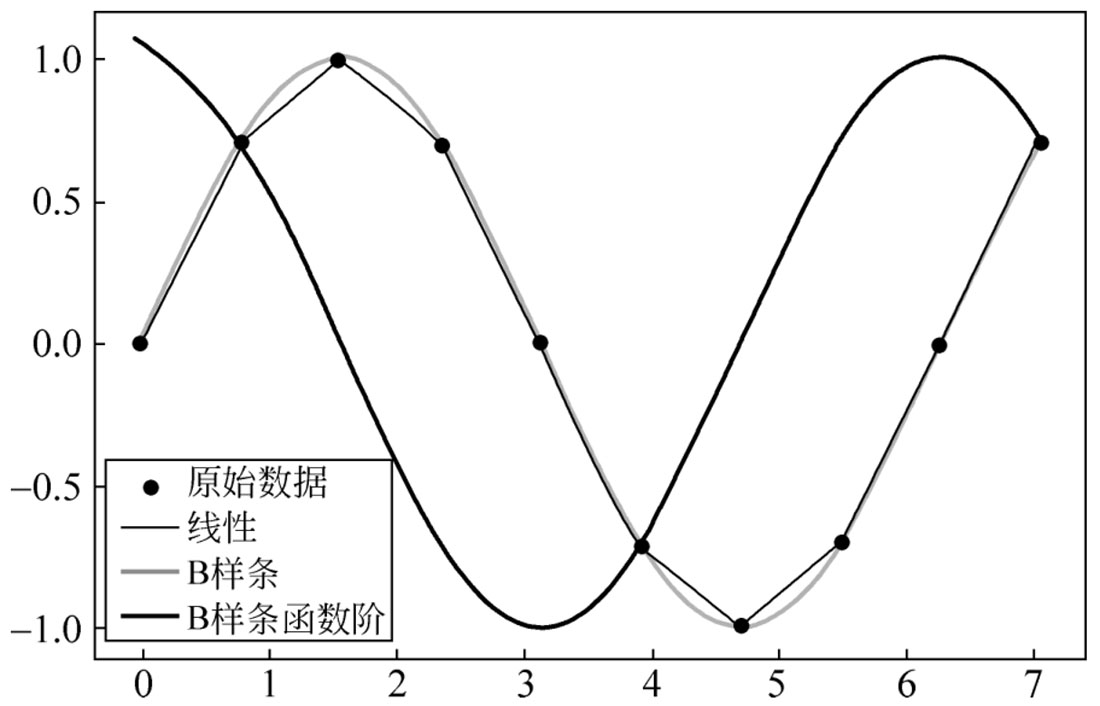
图2-3 样条插值
多维插值使用的是griddata()这个方法来进行二维空间插值。函数的语法格式为:
scipy.interpolate.griddata(points,values,xi,method='linear',fill_value=nan,rescale=
False)
其中,各参数含义如下。
· points:为散点自变量值(矩阵)。
· values:散点图对应函数值(可以有多个函数值)。
· xi:插值点自变量取值。
· method:插值实现方法,和一维、二维类似,一般有linear和nearest等插值方法。
· fill_value:设置为True,当xi不在给定插值空间时,根据一定的算法计算出某个值,如果xi距离给定插值空间比较远,通常这个值误差很大。
· rescale:在执行插值之前是否将点重新缩放到单位立方体。
【例2-38】 利用griddata()函数实现二维空间插值。
import numpy as np
from scipy.interpolate import griddata
import matplotlib.pyplot as plt
from scipy import interpolate
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus']=False #显示负号
def func(x,y):
return x*(1-x)*np.cos(4*np.pi*x**2)*np.sin(4*np.pi*y**2)
grid_x,grid_y=np.mgrid[0:1:100j,0:1:100j] #形成1×1的等间隔格网
points=np.random.rand(1000,2) #生成1000×2的随机数,值介于[0,1]
value=func(points[:,0],points[:,1]) #代入第一列和第二列
grid_zli=griddata(points,value,(grid_x,grid_y),method= 'linear')#将点和值插到网格中,
#方法为线性
grid_zCu=griddata(points,value,(grid_x,grid_y),method='cubic')
grid_znea=griddata(points,value,(grid_x,grid_y),method='nearest')
plt.figure() #开始产生图形
plt.subplot(221) #设置副图的位置
fig1=plt.imshow(func(grid_x,grid_y),extent=(0,1,0,1),origin='lower',cmap='spring)' #展示图
#片,cmap配色为spring,origin为配置原点,默认为upper不符合习惯
plt.plot(points[:,0],points[:,1],'k.',ms=1) #将点显示到图上
plt.colorbar(fig1) #对fig1配置colorbar
plt.title('原始数据') #图像题目设置成Original
plt.subplot(222)
fig2=plt.imshow(grid_zli.T,extent=(0,1,0,1),origin='lower',cmap='summer')
plt.colorbar(fig2)
plt.title('线性插值')
plt.subplot(223)
fig3=plt.imshow(grid_zCu.T,extent=(0,1,0,1),origin='lower',cmap='autumn')
plt.colorbar(fig3)
plt.title('立方插值')
plt.subplot(224)
fig4=plt.imshow(grid_znea.T,extent=(0,1,0,1),origin='lower',cmap='winter')
plt.colorbar(fig4)
plt.title('近邻插值')
plt.gcf().set_size_inches(6,6)
plt.show()
运行程序,效果如图2-4所示。
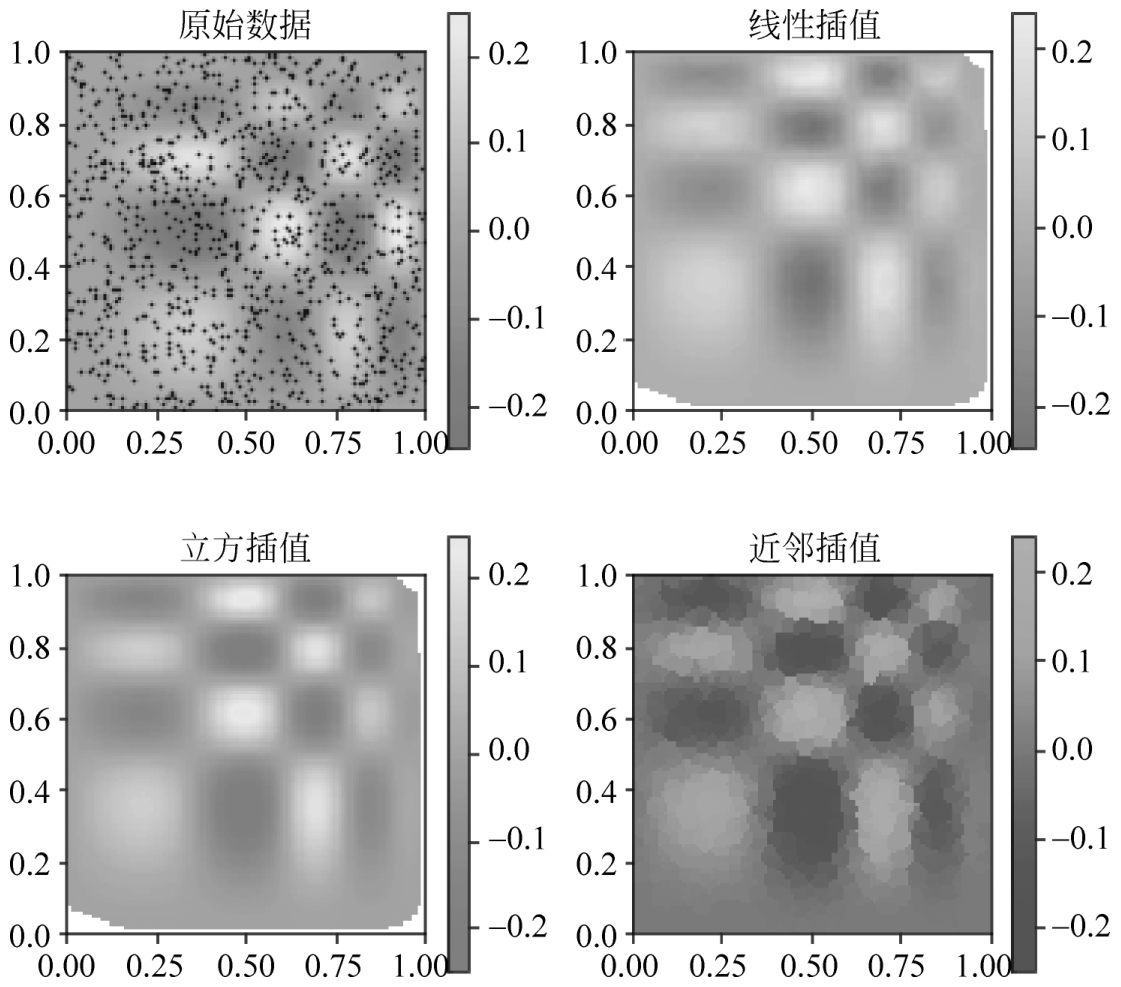
图2-4 二维空间插值效果
scipy.stats模块包含大量概率分布函数,主要有连续分布、离散分布以及多变量分布。除此之外,还有摘要统计、频率统计、转换和测试等多个小分类。基本涵盖了统计应用的方方面面。
下面以比较有代表性的scipy.stats.norm正态分布连续随机变量函数进行介绍。尝试使用rvs方法随机抽取1000个正态分布样本,并绘制出条形图。
from scipy.stats import norm
plt.hist(norm.rvs(size=1000))
运行程序,输出如下,效果如图2-5所示。
(array([ 3., 13., 57., 165., 247., 278., 171., 49., 13., 4.]),
array([-3.61411861,-2.89933072,-2.18454282,-1.46975493,-0.75496703,
-0.04017913, 0.67460876, 1.38939666, 2.10418455, 2.81897245,
3.53376035]),
<a list of 10 Patch objects>)
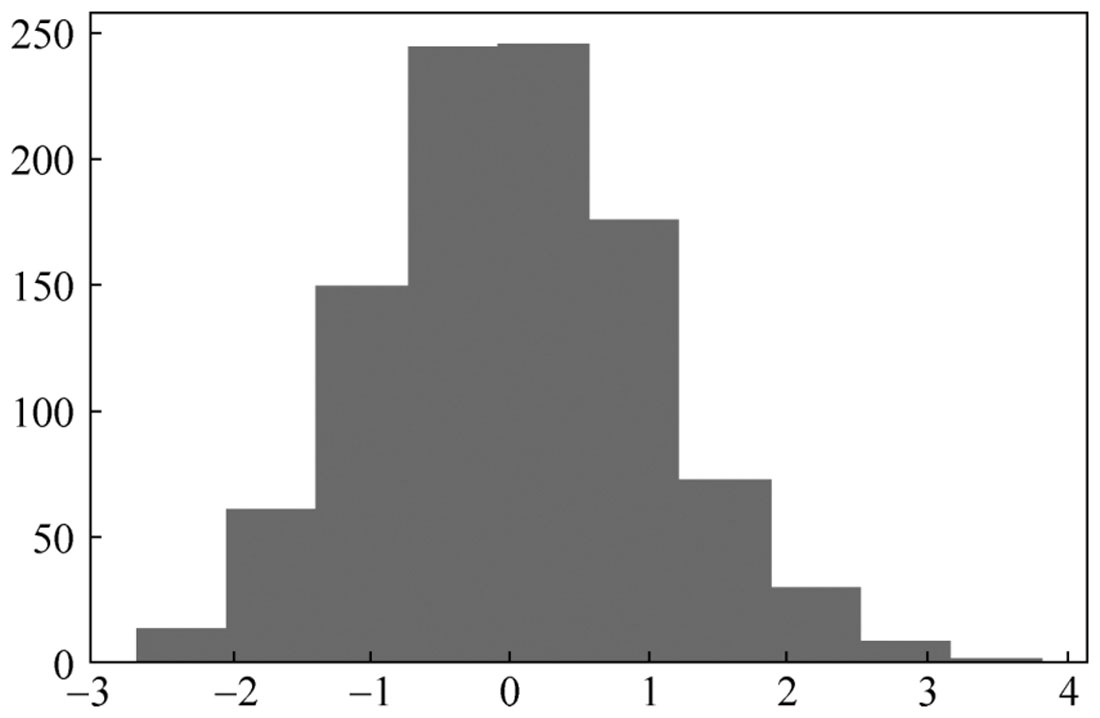
图2-5 正态分布图
当已知连续型随机变量分布函数时,对其求导就可得到密度函数。分布函数是概率统计中重要的函数,通过它可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征,分布函数可以完整地描述随机变量的统计规律,并且决定随机变量的一切其他概率特征。
柯西分布的分布函数为:
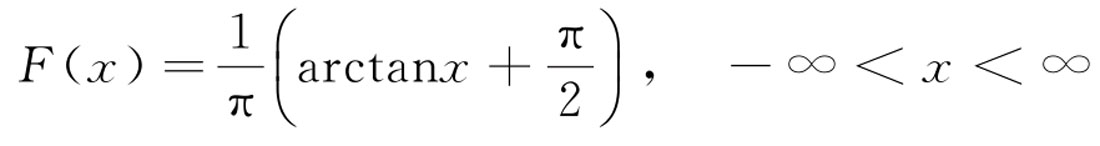
即柯西分布的密度函数为:
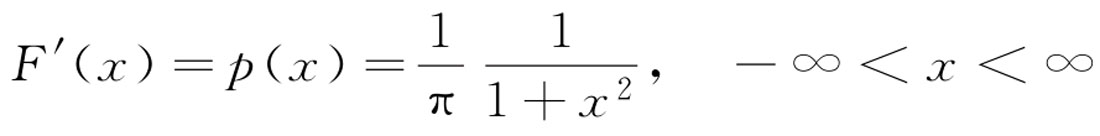
【例2-39】 根据柯西分布的分布函数求密度函数。
from sympy import*
x=symbols('x')
p_x=1/pi*(1/(1+x**2))#柯西分布的分布函数
integrate(p_x,(x,-oo,x))
#已知柯西分布的分布函数求密度函数
f_x=1/pi*(atan(x)+pi/2)
print(diff(f_x,x,1))
运行程序,输出如下。
1/(pi*(x**2+1))
如果随机变量 X 的密度函数为:
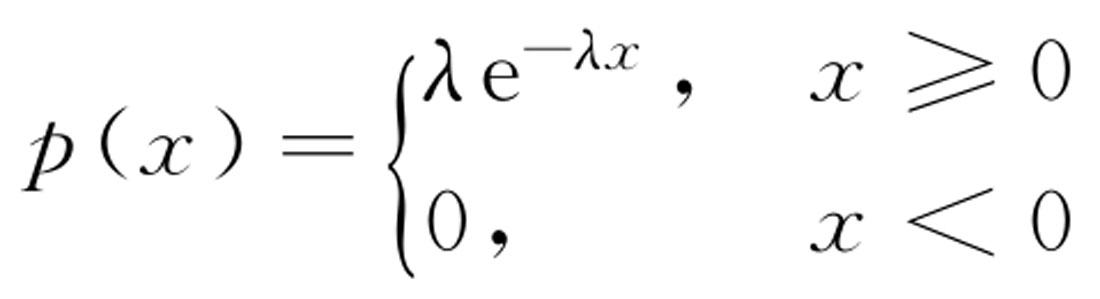
则称 X 服从指数分布,记作 X ~exp( λ ),其中,参数 λ >0( λ 是根据实际背景而定的正参数)。假如某连续随机变量 X ~exp( λ ),则表示 X 仅可能取非负实数。
指数分布的分布函数为:
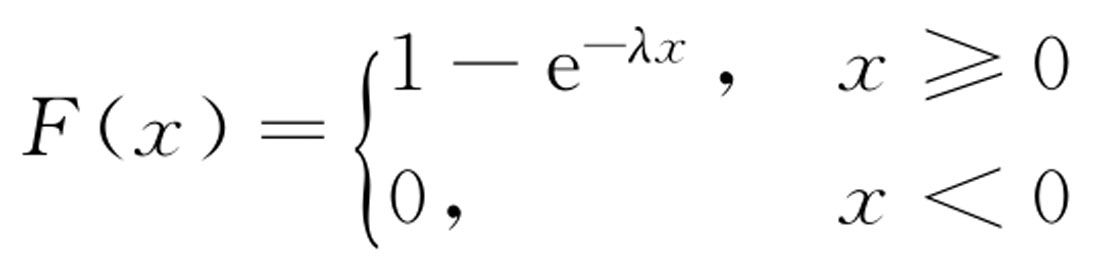
实际中不少产品首次发生故障(需要维修)的时间服从指数分布。例如,某种热水器首次发生故障的时间 T (单位:h)服从指数分布exp(0.002),即 T 的密度函数为:
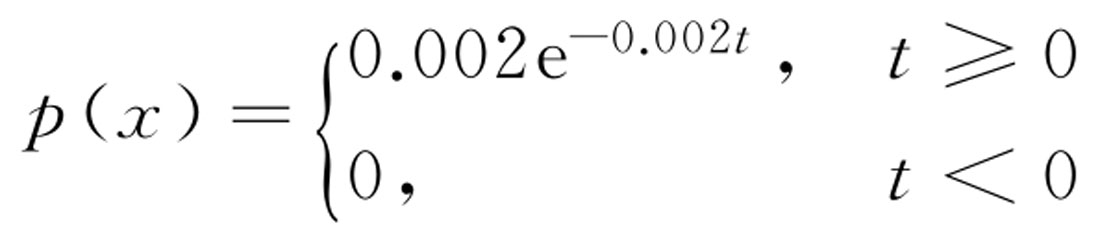
【例2-40】 指数分布实现。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #显示负号
#指数分布
lam=float(1.5)
x=np.linspace(0,15,100)
y=lam*np.e**(-lam*x)
plt.plot(x,y,"b",linewidth=2)
plt.xlim(-5,10)
plt.xlabel('X')
plt.ylabel('p(x)')
plt.title('指数分布')
plt.show()
运行程序,效果如图2-6及图2-7所示。
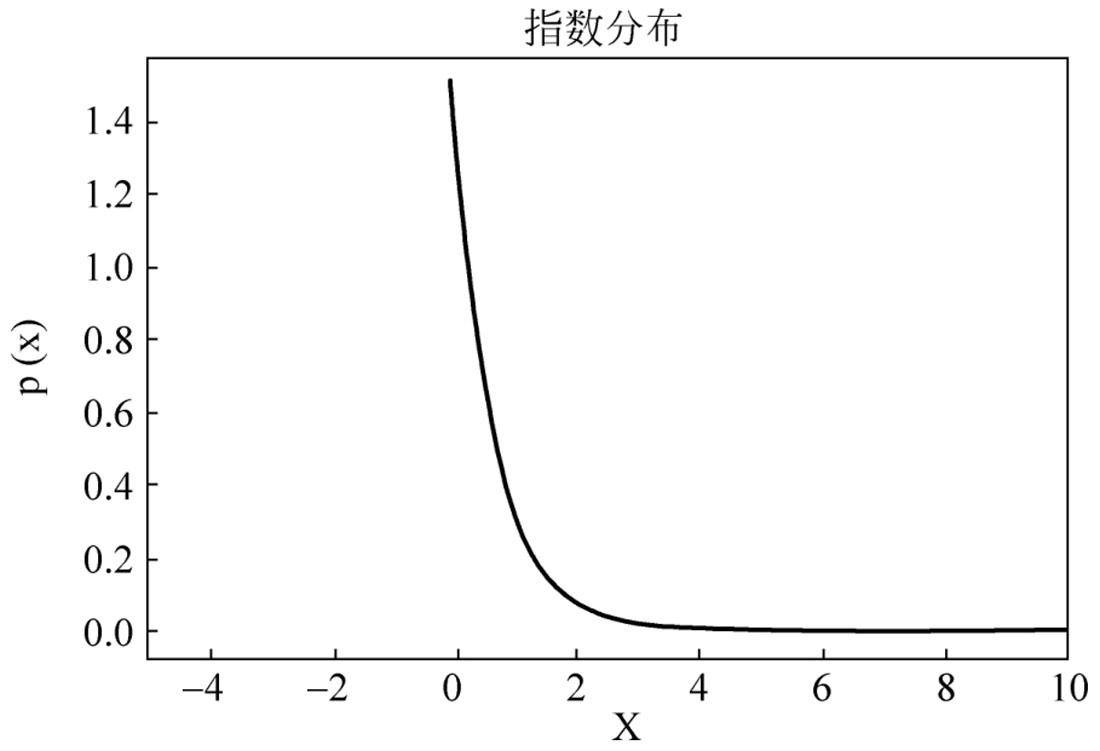
图2-6 指数分布
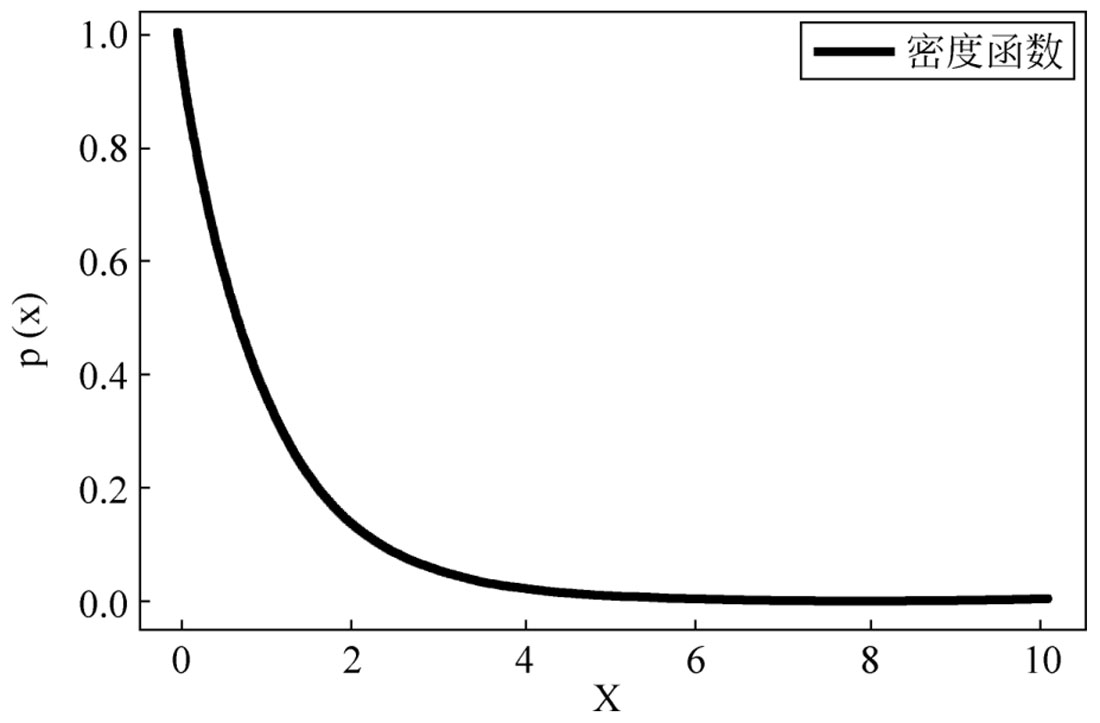
图2-7 密度函数
#使用SciPy计算PDF画图(非自定义函数)
from scipy.stats import expon #指数分布
x=np.linspace(0.01,10,1000)
plt.plot(x,expon.pdf(x),'r-',lw=5,alpha=0.6,label='密度函数')#PDF表示求密度函数值
plt.xlabel("X")
plt.ylabel("p(x)")
plt.legend()
plt.show()
二项分布有数个结果,因此是离散的。二项分布必须满足以下三个条件。
(1)观察或实验的次数是固定的。换句话说,如果做了一定次数,只能计算出某件事发生的概率。
(2)每次观察或实验都是独立的。换句话说,任何实验对下一次实验的概率都没有影响。
(3)每次实验成功的概率都是一样的。
二项分布的一个直观解释是投掷10次硬币。如果是一枚均匀硬币,得到正面的概率是0.5。现在扔硬币10次,数一数出现正面的次数。大多数情况下,得到正面5次,但也有可能得到正面9次。如果说 N =10, p =0.5,那么二项分布的PMF将给出这些概率。设正面的 x 是1,反面的 x 是0。
伯努利分布是二项分布的一种特例。伯努利分布中的所有值不是0就是1。
二项分布的概率函数为:
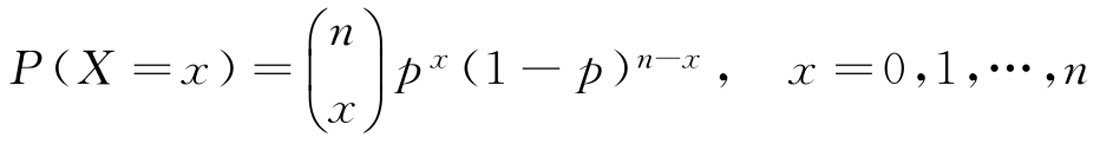
【例2-41】 某特效药的临床有效率为0.95,今有10人服用,问至少有8人治愈的概率是多少?
解析: 设 X 为10人中被治愈的人数,则 X ~ b (10,095),而所求概率为:
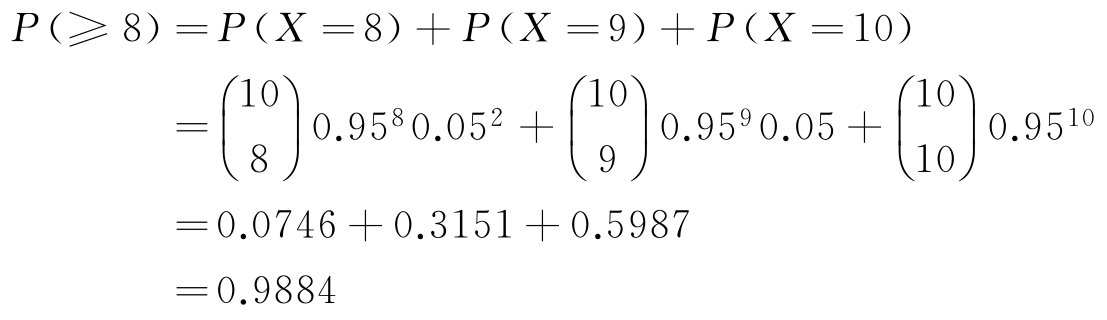
所以,10人中至少有8人被治愈的概率为0.9884。
以上例子,也可以抛硬币10次,用scipy.stats.binom进行画图。
#使用SciPy的PMF和CDF画图
from scipy.stats import binom
n=10
p=0.5
x=np.arange(1,n+1,1)
pList=binom.pmf(x,n,p)
plt.plot(x,pList,marker='o',alpha=0.7,linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
vline(x坐标值,y坐标最小值,y坐标最大值)
'''
plt.vlines(x,0,pList)
plt.xlabel('随机变量:抛硬币10次')
plt.ylabel('概率')
plt.title('二项分布:n=% d,p=% 0.2f' % (n,p))
plt.show()
运行程序,效果如图2-8所示。
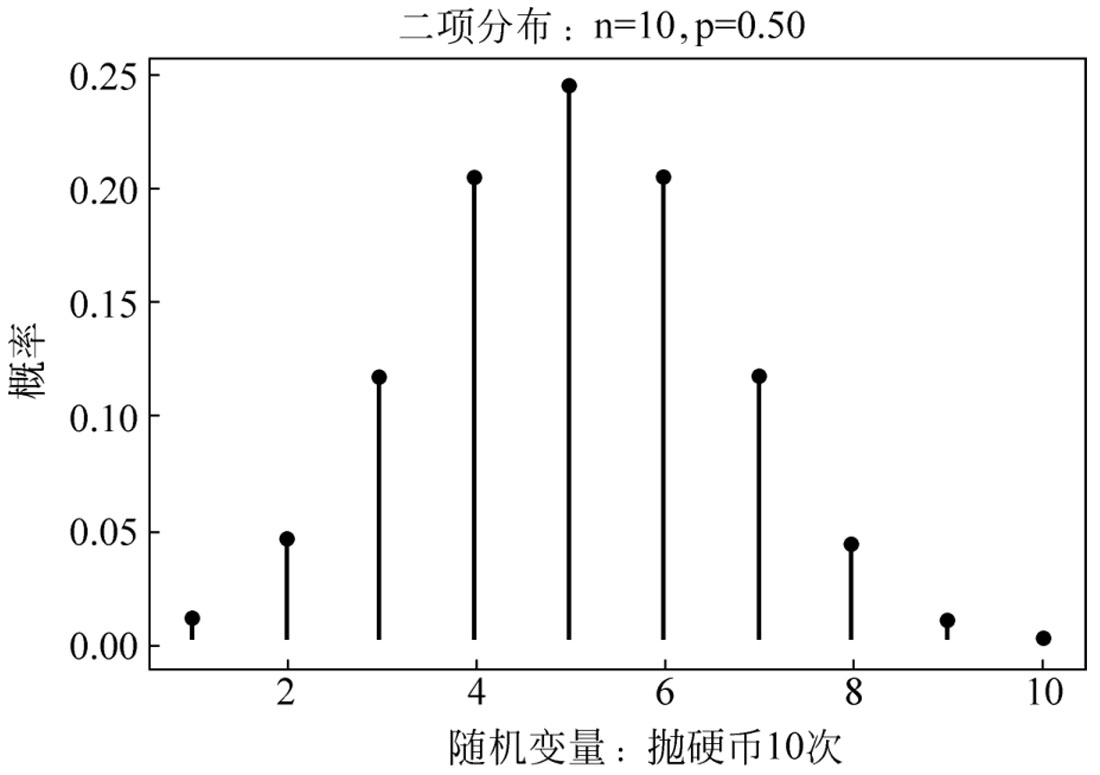
图2-8 二项分布
至于其他的泊松分布、正态分布以及均值分布等,因为篇幅原因在此不再展开介绍,下面通过一个例子来综合演示各概率分布。
【例2-42】 演示各种密度分布函数以及相应的期望与方差。


运行程序,输出如下。
0-1分布的数字特征:均值:0.5;方差:0.25;标准差:0.5
二项分布b(100,0.5)的数字特征:均值:50.0;方差:25.0;标准差:5.0
泊松分布P(0.6)的数字特征:均值:0.6;方差:0.6;标准差:0.7745966692414834
特定离散随机变量的数字特征:均值:3.5;方差:2.916666666666666;标准差:1.707825127659933
均匀分布U(1,1+5)的数字特征:均值:3.5;方差:2.083333333333333;标准差:1.4433756729740643
正态分布N(0,0.0001)的数字特征:均值:0.0;方差:0.0001;标准差:0.01
指数分布Exp(5)的数字特征:均值:0.2;方差:0.04000000000000001;标准差:0.2
标准正态分布的数字特征:均值:-5.955875168377274e-16;方差:0.9999999993069072;标准差:
0.9999999996534535
Exp(5.0)分布的数字特征:均值:0.2082620293848526;方差:0.03678416218397953;标准差:0.19179197632846773
dist分布的数字特征:均值:3.333333333333333;方差:1.388888888888891;标准差:1.1785113019775801
大数定律主要有两种表达方式,分别如下。
设
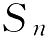 为
n
重伯努利实验(结果只有0和1)中事件A发生的次数,
为
n
重伯努利实验(结果只有0和1)中事件A发生的次数,
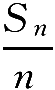 就是事件A发生的频率,
p
为每次实验中A出现的概率,则对任意的
ε
>0,有
就是事件A发生的频率,
p
为每次实验中A出现的概率,则对任意的
ε
>0,有
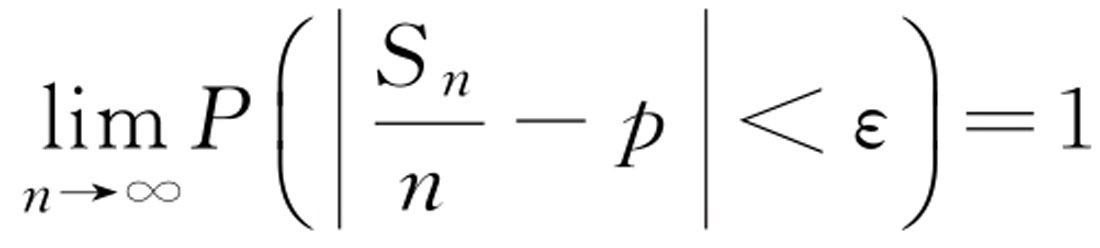
设{
X
n
}为一独立同分布的随机变量序列,如果
X
i
的数学期望存在,则{
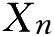 }服从大数定律,即对任意的
ε
>0,
}服从大数定律,即对任意的
ε
>0,
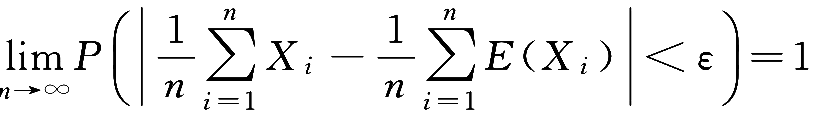 成立。
成立。
对于独立同分布且具有相同均值
μ
的随机变量
X
1
,
X
2
,…,
X
n
,当
n
很大时,它们的算术平均数
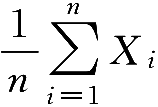 很接近于
μ
。也就是说,可以使用样本的均值去估计总体均值。
很接近于
μ
。也就是说,可以使用样本的均值去估计总体均值。
对于简单问题来说,蒙特卡洛方法是个“笨”办法。但对许多问题来说,它往往是个有效,有时甚至是唯一可行的方法。但对于涉及不可解析函数或概率分布的模拟及计算,蒙特卡洛方法是个有效的方法。
我们都玩过套圈圈的游戏,但是你想过为什么总是套不上吗?下面用蒙特卡洛方法来算一算。
(1)设物品中心点坐标为(0,0),物品半径为5cm。
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
circle_target=mpatches.Circle([0,0],radius=5,edgecolor='r',fill=False)
plt.xlim(-80,80)
plt.ylim(-80,80)
plt.axes().add_patch(circle_target)
plt.show() #效果如图2-9(a)所示
(2)设投圈半径为8cm,投圈中心点围绕物品中心点呈二维正态分布,均值 μ =0cm,标准差 σ =20cm,模拟1000次投圈过程。
#matplotlib inline
N=1000
u,sigma=0,20
points=sigma * np.random.randn(N,2)+u
#效果如图2-9(b)所示
plt.scatter([x[0]for x in points],[x[1]for x in points],c=np.random.rand(N),alpha=0.5)
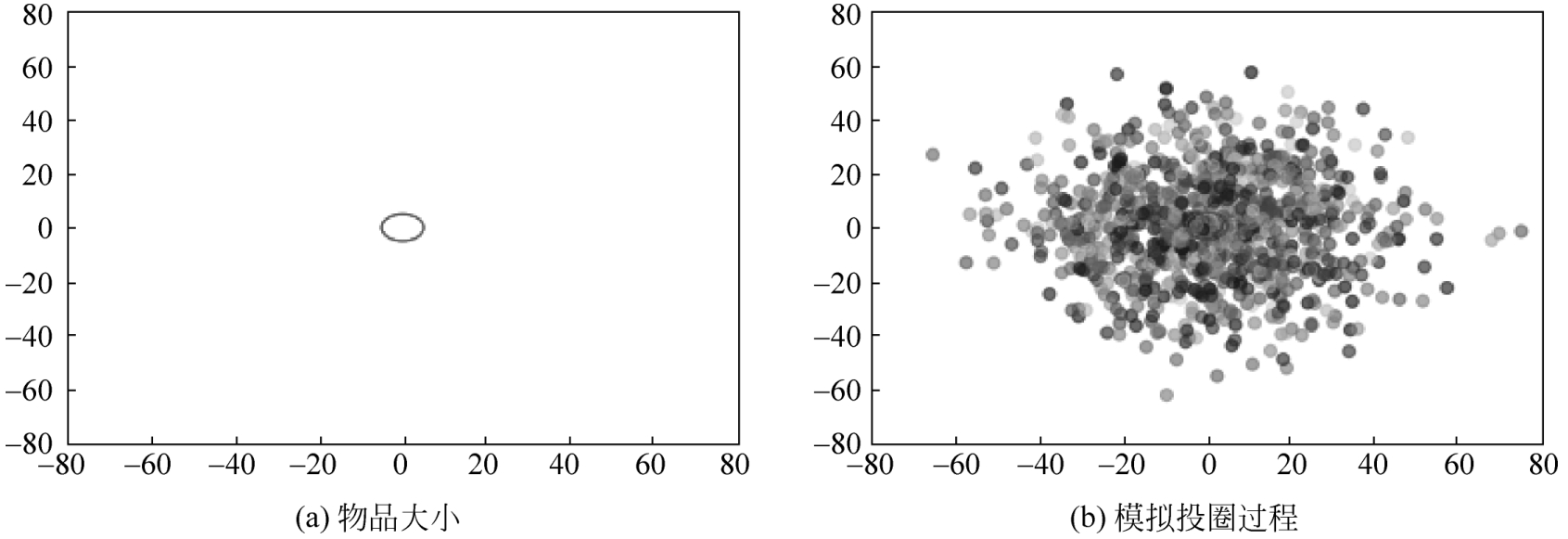
图2-9 蒙特卡洛方法模拟投圈过程
图2-9中红圈为物品,散点图为模拟1000次投圈过程中,投圈中心点的位置散布。
(3)计算1000次投圈过程中,投圈套住物品的占比情况。
print(len([xy for xy in points if xy[0]**2+xy[1]**2<(8-5)**2])/N)
输出结果:0.013。即投1000次,有13次能够套住物品,就是个小概率事件,现在知道投圈为什么那么难套住了吧?
中心极限定理是概率论中讨论随机变量序列部分和的分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,研究由许多独立随机变量组成和的极限分布律,指出了大量随机变量近似服从正态分布的条件。
大数定律讨论的是在什么条件下(独立同分布且数学期望存在),随机变量序列的算术平均概率收敛到其均值的算术平均。下面来讨论在什么情况下,独立随机变量的和
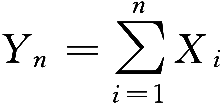 的分布函数会分布收敛于正态分布。下面使用一个小例子来说明什么是中心极限定理。
的分布函数会分布收敛于正态分布。下面使用一个小例子来说明什么是中心极限定理。
研究一个复杂工艺产生的产品误差的分布情况,诞生该产品的工艺中,有许多方面都能产生误差,例如,每个流程中所需的生产设备的精度误差、材料实际成分与理论成分的差异带来的误差、工人当天的专注程度、测量误差等。由于这些因素非常多,每个影响产品误差的因素对误差的影响都十分微小,而且这些因素的出现也十分随机,数值有正有负。现在将每一种因素都假设为一个随机变量
X
i
,先按照直觉假设
X
i
服从
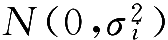 ,零均值假设是十分合理的,因为这些因素的数值有正有负,假设每一个因素的随机变量的方差
,零均值假设是十分合理的,因为这些因素的数值有正有负,假设每一个因素的随机变量的方差
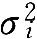 是随机的。接下来,希望研究的是产品的误差
Y
n
=
X
1
+
X
2
+…+
X
n
,当
n
很大时是什么分布?
是随机的。接下来,希望研究的是产品的误差
Y
n
=
X
1
+
X
2
+…+
X
n
,当
n
很大时是什么分布?
#模拟n个正态分布的和的分布
from scipy.stats import norm
def Random_Sum_F(n):
sample_nums=10000
random_arr=np.zeros(sample_nums)
for i in range(n):
mu=0
sigma2=np.random.rand()
err_arr=norm.rvs(size=sample_nums)
random_arr+=err_arr
plt.hist(random_arr)
plt.title("n="+str(n))
plt.xlabel("x")
plt.ylabel("p(x)")
plt.show()
Random_Sum_F(2)
Random_Sum_F(10)
Random_Sum_F(100)
Random_Sum_F(1000)
运行程序,效果如图2-10所示。
如果正态分布实验没发现规律,还可以去尝试泊松分布、指数分布等,最终实验说明:假设{ X n }独立同分布、方差存在,不管原来的分布是什么,只要 n 充分大,就可以用正态分布去逼近随机变量和的分布,所以这个定理有着广泛的应用。接下来一起来研究如何使用中心极限定理产生一组正态分布的随机数。
计算机往往只能产生一组随机均匀分布的随机数,那么如果想要产生一组服从正态分布 N ( μ , σ 2 )的随机数,应该如何操作呢?设随机变量 X 服从(0,1)上的均匀分布,则其数学期望与方差分别为1/2和1/12。由此得12个相互独立的(0,1)上均匀分布随机变量的数学期望与方差分别为6和1。因此:
(1)产生12个(0,1)上均匀分布的随机数,记为 x 1 , x 2 ,…, x 12 。
(2)计算 y = x 1 + x 2 +…+ x 12 -6,则由中心极限定理知,可将 y 近似看成来自标准正态分布 N (0,1)的一个随机数。
(3)计算 z = μ + σ y ,则可将 z 看成来自正态分布 N ( μ , σ 2 )的一个随机数。
(4)重复 N 次就能获得 N 个服从正态分布 N ( μ , σ 2 )的随机数。
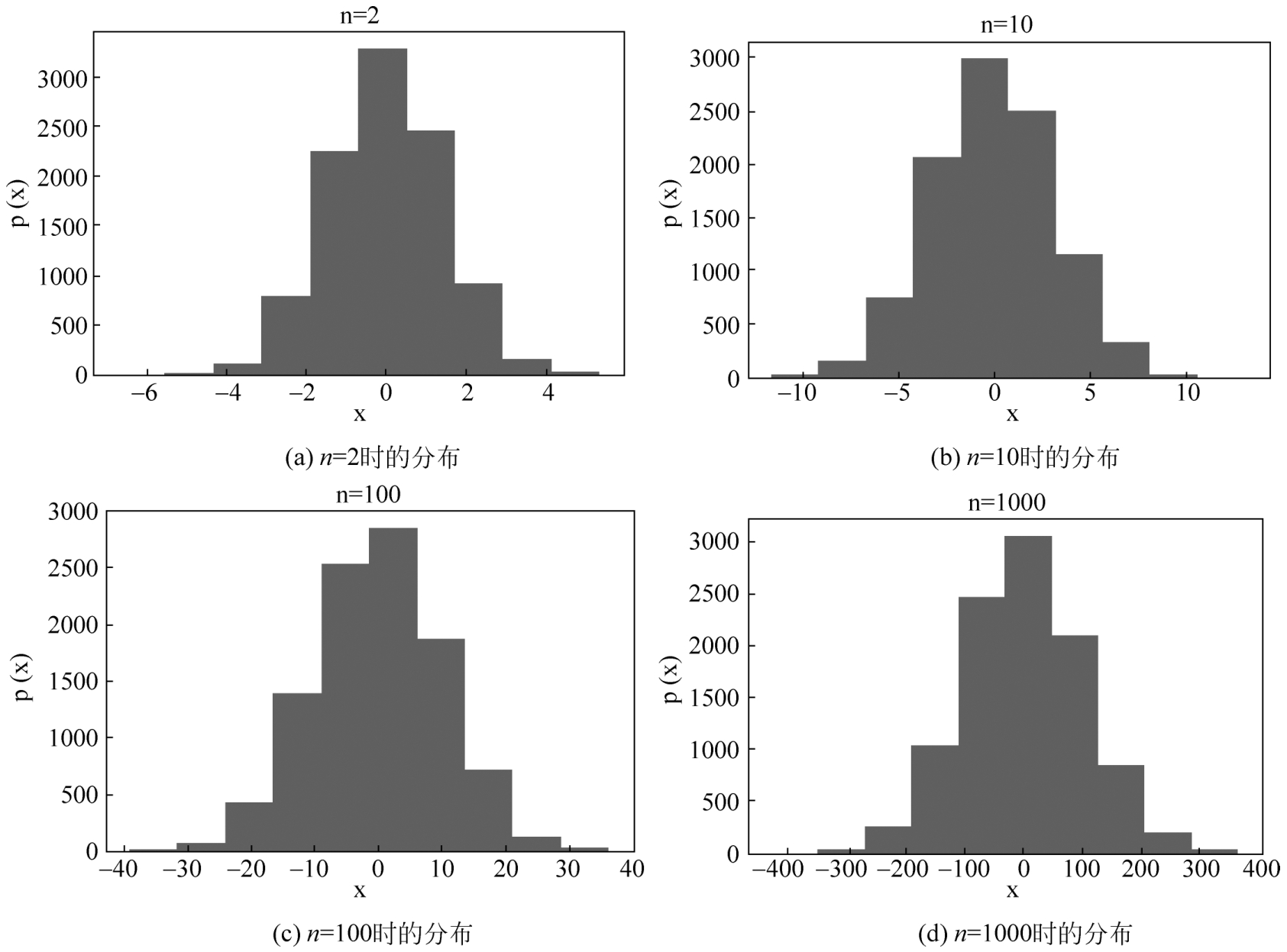
图2-10 不同 n 值的正态分布效果