




数独的解题技巧大致可分为直观法和候选数法两种。
直观法不需任何辅助工具,玩数独谜题时只需有一支笔。直观法是初学者或没有计算机辅助时的首选解题方法。相对而言,能解出的谜题也比较简单。
候选数法需先对候选数列表,所以解答数独谜题时常需要计算机辅助,或使用候选数法的辅助解题用纸,需经过一段相当长的时间才会出现第一个解。候选数法是使用高阶直观法技巧或有计算机辅助时的首选解题方法。相对而言,能解出较复杂的谜题。
数独的解谜技巧刚开始发展时,以易于上手的直观式解法为主。对于初入门的人来说,这也是较容易理解和接受的方法。其实就算是资深的高手,当身边没有计算机协助更新候选数列表时,大多数仍会采用直观法,因为候选数列表的建立及更新若采用手动方式操作,一是十分烦琐,二是容易出错,而候选数法对于候选数列表的正确性要求是不能有一点误差的。一般报纸杂志上的数独谜题为了迎合大众,大抵属简易级或中级,如果能灵活运用直观法,通常解答起来游刃有余。但若是网站上的复杂数独谜题,则常常需用候选数法才能解出来。
基础摒除法就是利用1~9的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。基础摒除法可以分为九宫格摒除、列摒除、行摒除。
实际寻找解的过程如下。
(1)寻找九宫格摒除解:找到了某数在某一个九宫格中可填入的位置只余一个的情形,即找到了该数在该九宫格中的填入位置。
(2)寻找列摒除解:找到了某数在某列可填入的位置只余一个的情形,即找到了该数在该列中的填入位置。
(3)寻找行摒除解:找到了某数在某行可填入的位置只余一个的情形,即找到了该数在该行中的填入位置。
基础摒除法解题技巧示范如下。
(1)直射排除。具体如下。
因为行、列内的数字不能重复,所以用出现的数字就可以排除同行、同列的空白单元格内填入该数字的可能性,起到排除的作用。行、列排除像光线直接照射过去一样,故名为直射排除,见图(a)~(c)(提示:圆点处为排除后可以填入确定数字的位置,下同)。
(2)折射排除。具体如下。
利用直射排除法确定一个包含该数字的范围,再利用该范围去排除同行、同列内填入该数字的可能性,起到排除的作用。确定范围后再次更改方向进行排除,像光线折射后照射过去一样,故名为折射排除,见图(d)。
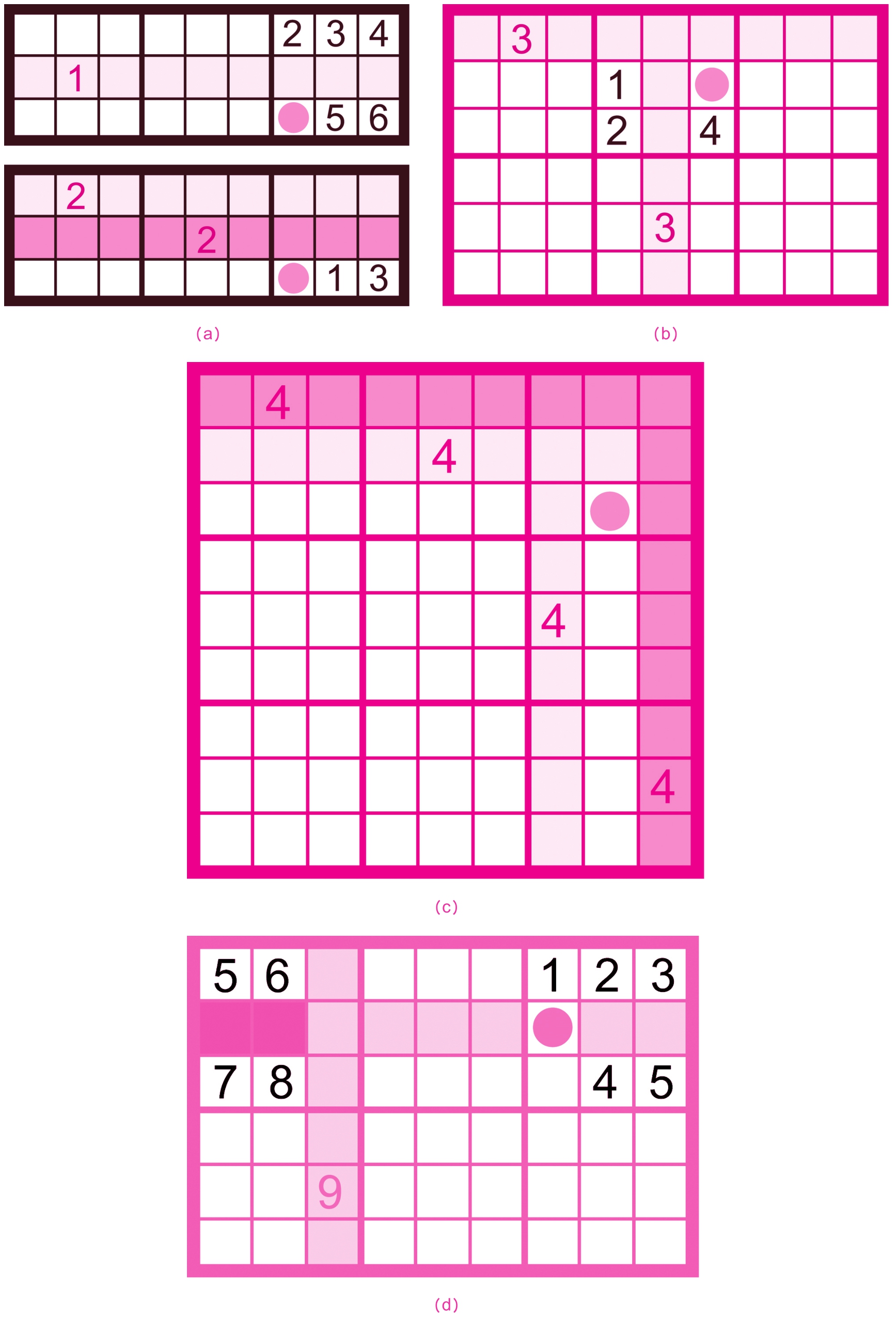
(3)散射排除。
因为宫内的数字不能重复,所以出现的数字就可以排除同宫的空白单元格内填入该数字的可能性,起到排除的作用。宫排除像光线发散照射过去一样,故名为散射排除,见图(e)。
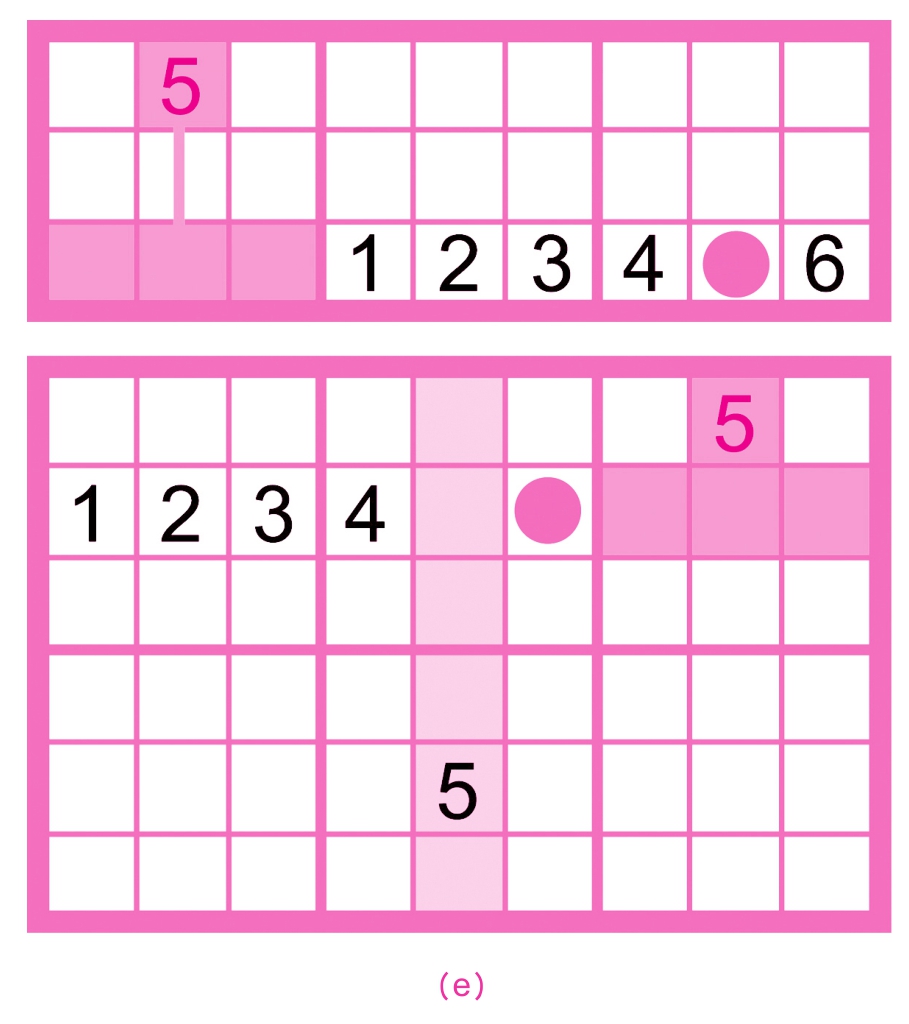
基础摒除法应用实例如下。

上图中,可以用基础摒除法确定(2,2)、(3,8)、(5,7)、(6,6)、(9,5)单元格的数字吗?

(1,4) = 9,第一行排除9;
(7,1) = 9,第一列排除9;
(4,3) = 9,第三列排除9。
提示: (1,4)表示第一行、第四列位置的单元格应填入的值,(7,1)表示第七行、第一列位置的单元格应填入的值。其他以此类推。
由基础摒除法可知,第一宫中只有一个唯一的位置(2,2)为9。
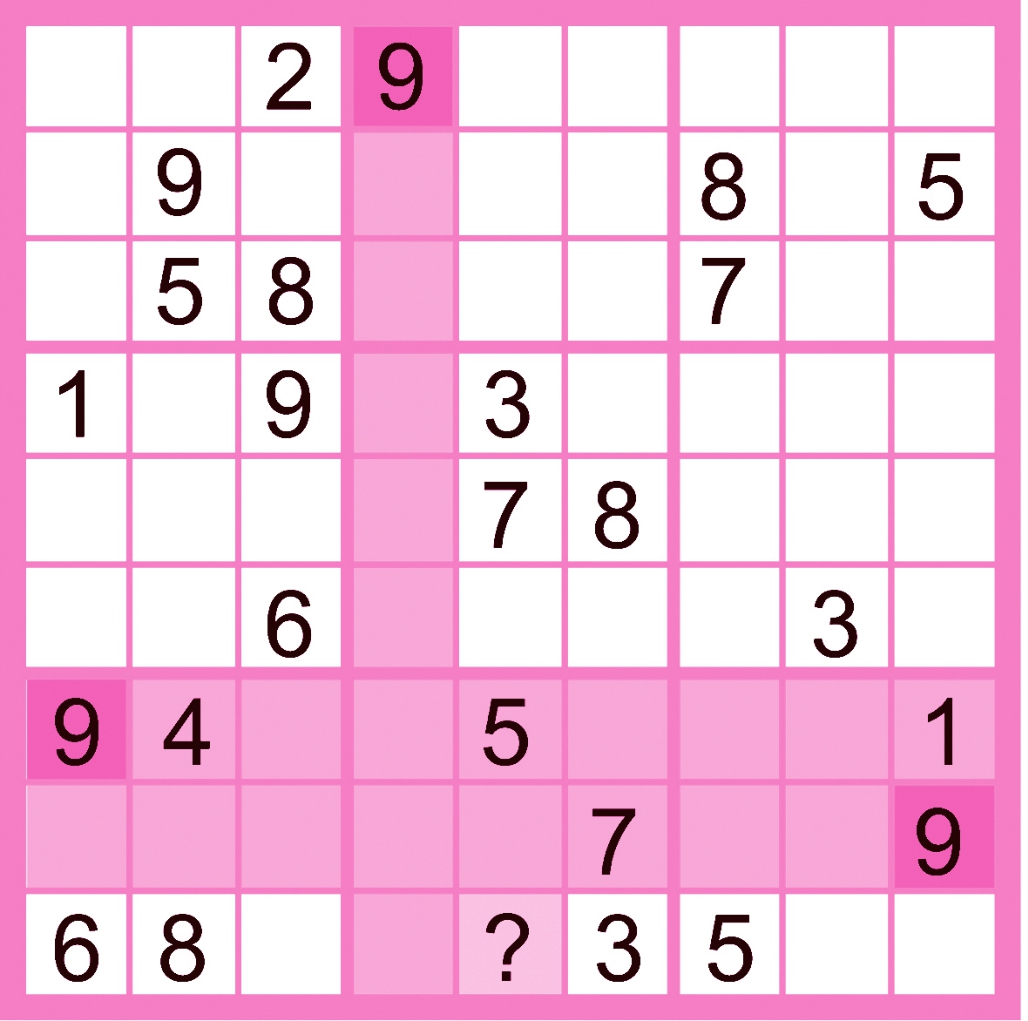
(1,4) = 9,第四列排除9;
(7,1) = 9,第七行排除9;
(8,9) = 9,第八行排除9。
由基础摒除法可知,第八宫中只有一个唯一的位置(9,5)为9。

(1,4) = 9,第四列排除9;
(4,3) = 9,第四行排除9;
(9,5) = 9,第五列排除9。
由基础摒除法可知,第五宫中只有一个唯一的位置(6,6)为9。

(1,4) = 9,第一行排除9;
(2,2) = 9,第二行排除9;
(8,9) = 9,第九列排除9。
由基础摒除法可知,第三宫中只有一个唯一的位置(3,8)为9。

(4,3) = 9,第四行排除9;
(6,6) = 9,第六行排除9;
(3,8) = 9,第八列排除9;
(8,9) = 9,第九列排除9。
由基础摒除法可知,第六宫中只有一个唯一的位置(5,7)为9。
单元摒除法虽属于进阶的技巧,但已入门的人在解题时,可以很容易地配合基础摒除法使用,以增加找到解的机会。所以,即使是初级的题目,在解题时也可以应用此法,并非在用基础摒除法找不到解时才用此法。
单元摒除法应用实例如下。

你能在上图的第一宫中找到数字1的填入位置吗?

由于(8,6)的列摒除,使得数字1可填入第二宫的位置只剩下(1,4)及(2,5)。另外,由于(6,9)和(9,7)的列摒除,使得数字1可填入第三宫的位置只剩下(1,8)和(2,8)。因为这4个宫格恰好在相同的两列上,所以第二宫的数字1填在(1,4)位置上是不行的,因为第一行只能有一个数字1,所以第三宫的数字1就只能填到(2,8)位置上;如果第二宫的数字1填在(2,5)位置上,而第二行只能有一个数字1,那么第三宫的数字1就只能填到(1,8)位置上。
无论产生哪一种情况,第一行和第二行的数字1都只能填在第二宫和第三宫中,所以第一宫的第一行和第二行的数字1出现的可能性被摒除。

再配合(4,1)和(7,3)的基础列摒除,可得第一宫中数字1的位置只能在(3,2)。
区块摒除法是对基础摒除法的提升,是直观法中使用频率最高的方法之一。
所谓区块,就是指一个宫中的三个相连的小方块。这样行就可以分成3个区块,列也可以分成3个区块。九宫格同样可以分成3个区块,示意图如下。

行区块

列区块

宫格区块
区块摒除法的核心思想讲解如下。

假定我们已确定上图第一宫区块中含有数字9,第二宫区块中也含有数字9,则在第三宫区块中一定含有数字9。如果再通过其他方法确定第三宫区块中某两个宫格不能为数字9,则就能确定数字9在第三宫区块的具体位置了。
区块摒除法应用实例如下。

能使用区块摒除法确定上图中(6,6)的数字吗?

因为(4,9)=2,则第四宫中第二行区块或第三行区块中包含数字2。

又因为(2,1)=2,利用列摒除法,(5,1)、(6,1)不能为数字2。而(6,2)、(6,3)已填有数字,所以(5,2)、(5,3)必有数字2。

由上图得出第六宫区块、第四宫区块都包含数字2,这是典型的区块摒除法,得到第五宫区块包含数字2。

因为(7,4)=2的列摒除,且(6,5)已填入数字,所以(6,6)=2。
行唯一解:当某行已填数字的宫格达到8个,那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。
列唯一解:当某列已填数字的宫格达到8个,那么该列剩余宫格能填的数字就只剩下那个还没出现过的数字了。
九宫格唯一解:当某九宫格已填数字的宫格达到8个,那么该九宫格剩余宫格能填的数字就只剩下那个还没出现过的数字了。
唯一解法解题技巧示范如下。
因为同行、同列、同宫内的数字不能重复且为1~9,如果与一个单元格同行、同列、同宫并已经出现了8个已知数字,那么这个单元格就填入剩余的那个数字。

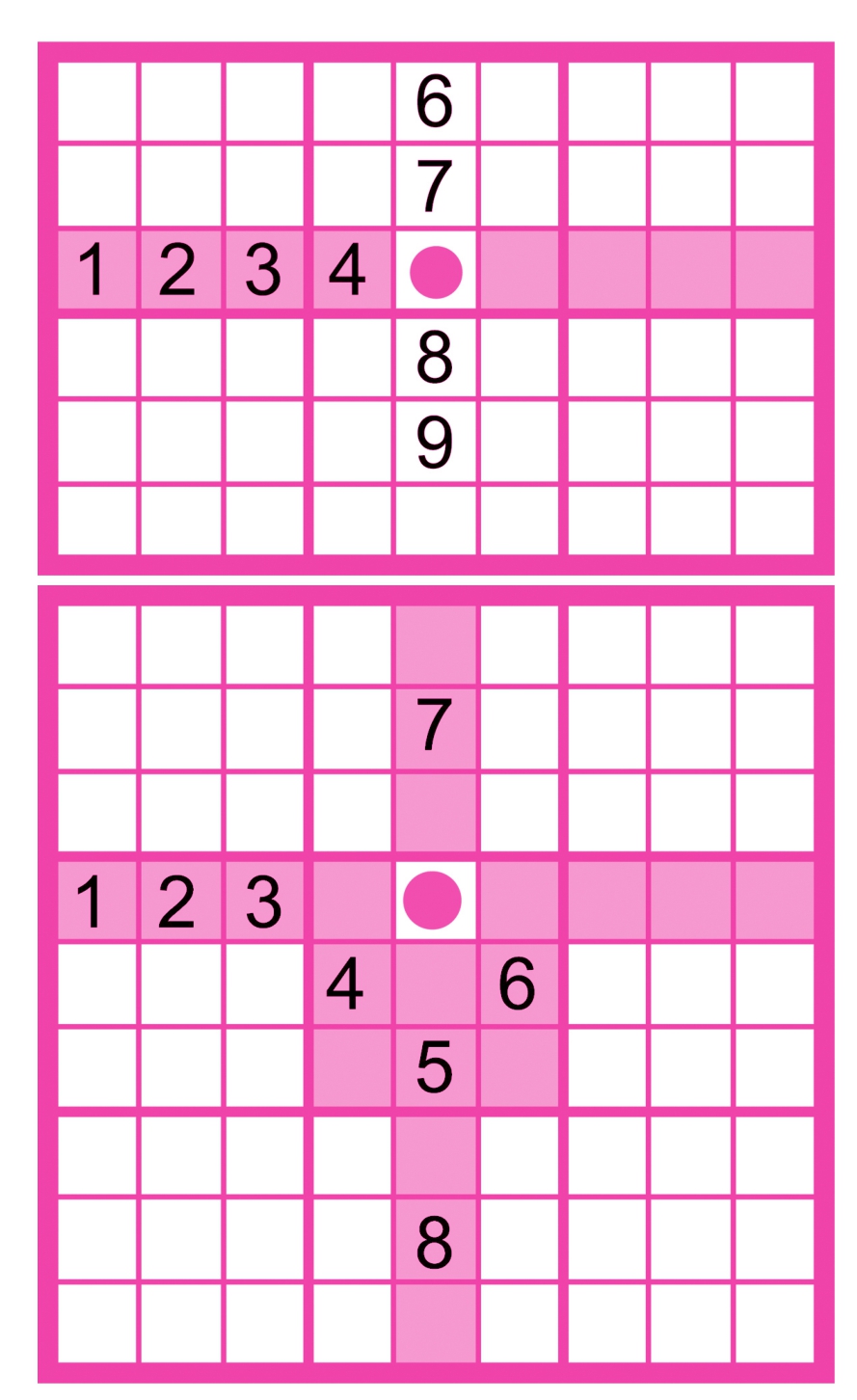
下面是唯一解法应用实例。

由上图可知,第一行填入了8个数字,第一行只有数字3没有出现过,所以(1,9)=3,这是行的唯一解。

由上图可知,第一列填入了8个数字,第一列只有数字5没有出现过,所以(5,1)=5,这是列的唯一解。
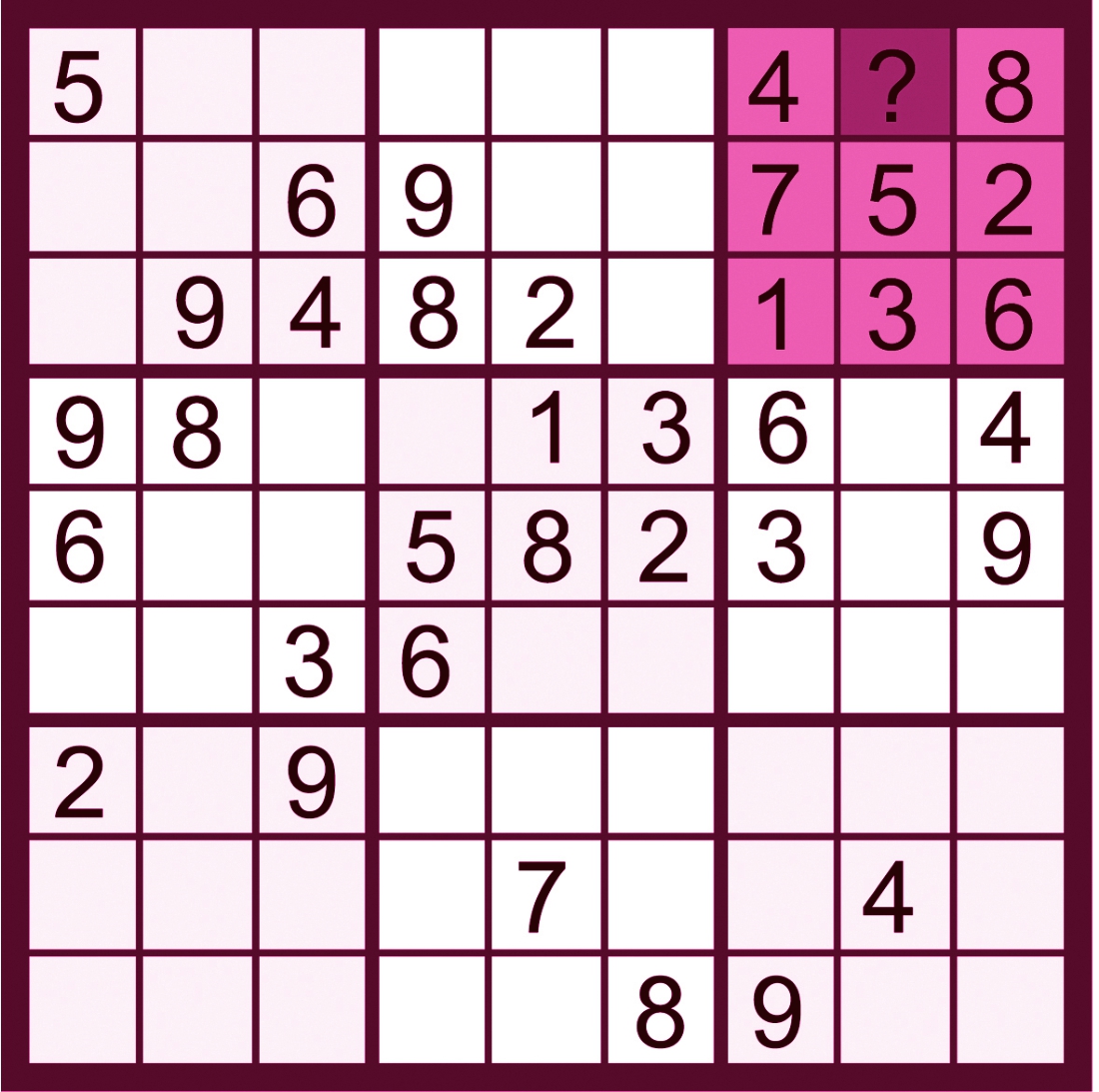
由上图可知,在第三宫中已经填入8个数字,只有数字9没有出现过,所以(1,8)=9,这是九宫格唯一解。
唯一解法道理非常简单,但在实际使用时比较困难,要注意识别,因为在实际应用时不会那么容易发现缺少的数字。

能使用唯一解法确定上图中(2,7)的值吗?
这道题也不算难。(2,7)所在的行、列及宫格综合来看,只缺少数字8。

能确定上图中(1,9)、(2,9)、(3,9)、(5,9)的值吗?

由(3,7)=9,可以得知(7,8)、(8,8)、(9,8)一定有一个是9,由区块摒除法可以得出(5,9)=9。
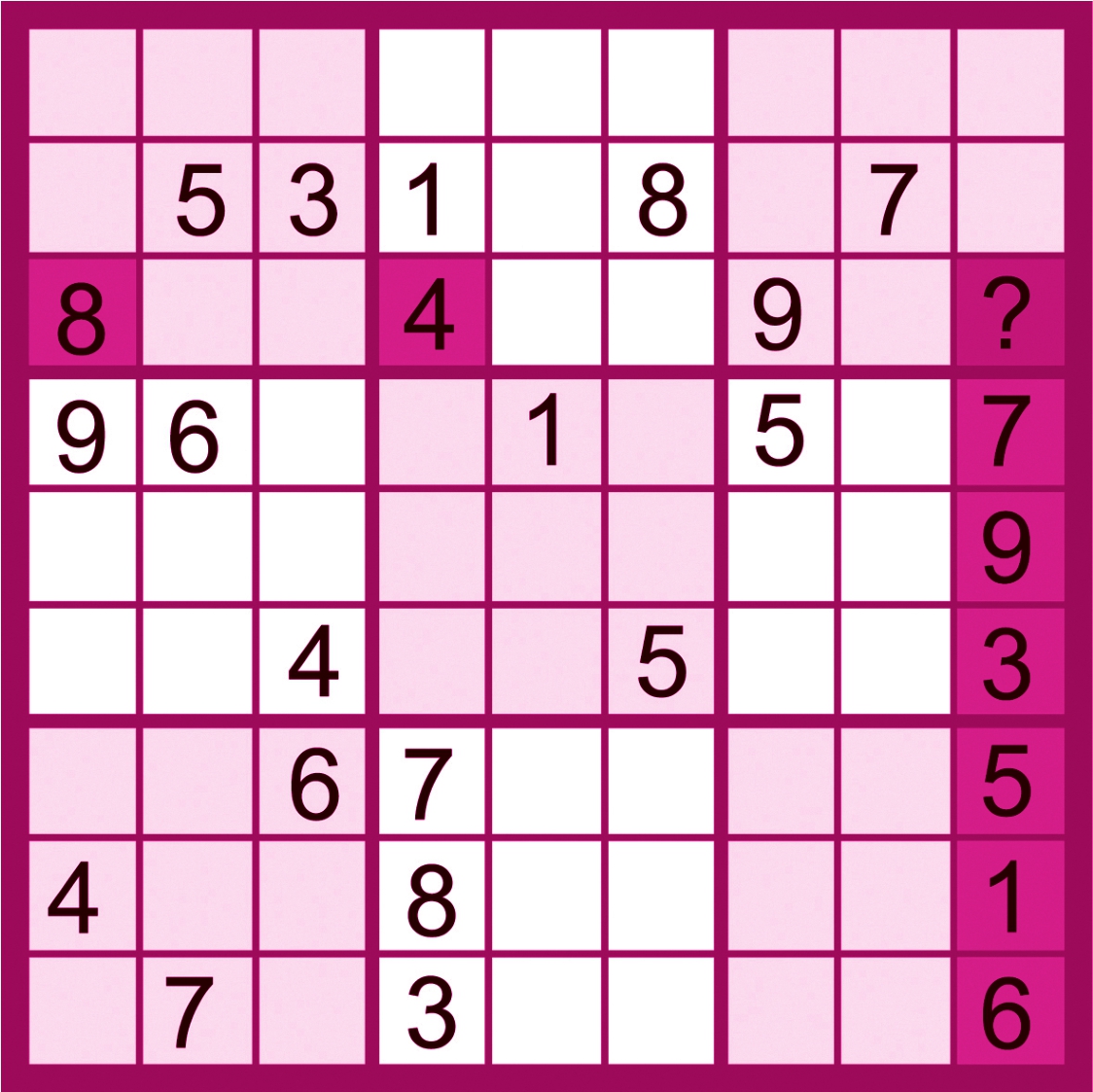
由唯一解法可得,(3,9)=2。

同样,可得出(2,9)=4,(1,9)=8。
余数测试法就是在某行、某列或某个九宫格中已经填上的数字比较多,只在剩下的2个或3个宫格中填入某个值进行测试的解题方法。
余数测试法应用实例如下。

在上图第二行和第三行中,剩余未填的数字只有两三个了,这时可以使用余数测试法进行解题。

在上图第二行中,(2,3)可以填入的数字为5或者6,所以先用5进行测试。

在(2,3)填入5以后,可以得到下图,没有得出出错的推断,所以(2,3)=5可能是正确的判断。

不过该题并没有解完,只找到一个合理的解还不够,还要能判断出(2,3)≠6,才能肯定(2,3)=5。
所以下面我们还要用(2,3)=6进行测试。
在(2,3)填入6后,可以推出(2,8)=5。
观察第三行,(3,7)、(3,8)、(3,9)必含有数字5。
因此,(2,3)=6是错误的,从而得出(2,3)=5。
候选数法是先建立候选数列表,根据各种条件,逐步安全地排除每个宫格候选数中不可能取值的数,直至剩下最后一个候选数,这个数字就是该宫格的解。
使用候选数法一般能解答比较复杂的数独题目。但是候选数法的使用没有直观法那么直接,需要先建立一个候选数列表。所以实际应用时可以先利用直观法进行解题,若无法用直观法解题时,再使用候选数法解题。
候选数法解题的过程就是逐渐排除不合适的候选数的过程,所以在进行候选数删除的时候一定要小心,确保安全地删除不合适的候选数,否则就只有重新做题了。
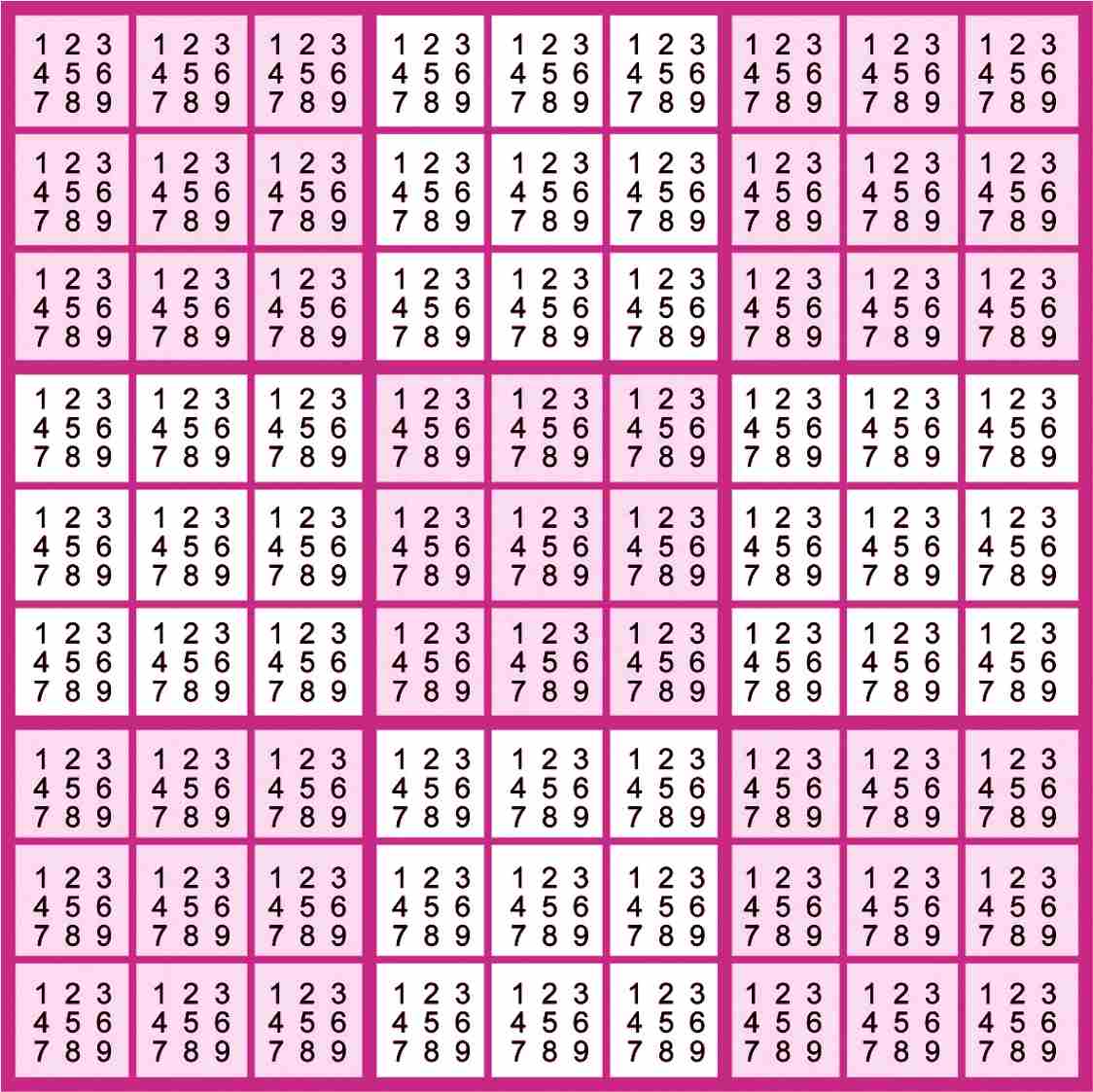
首先,我们来制作一张候选数表(见下图),其中每一个宫格中的数字1~9代表的是本宫格在解题时还可以填入的数字。如果某一个数字已被摒除在本宫格的可填入范围之内,就必须将其删除。所以当要在某个宫格中填入数字时,只要从该宫格的候选数中挑选即可,不在该宫格候选数中的数字是不可以填入该宫格中的。
下图是一个简单的数独谜题,数独中每填入一个数字,必须将该数字所处宫格的行、列及九宫格的相关各宫格的候选数都划掉。例如,当将数字5填入(1,7)后,必须将(1,7)的候选数全部删除,并将数字5从第一行、第七列及第三宫的各个宫格候选数中删除,因为这些宫格都已经不能再填入数字5了。
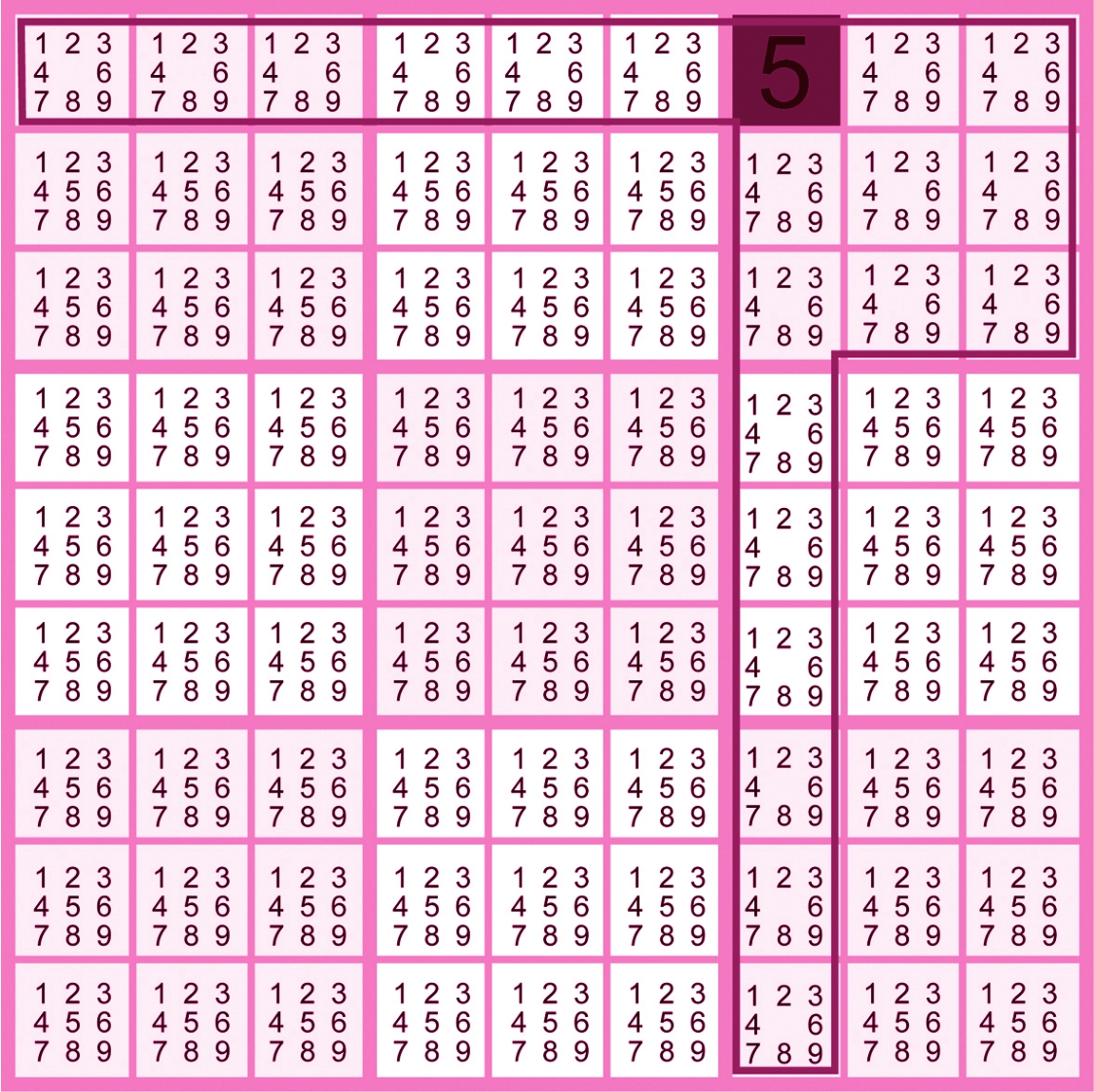
当所有已知数字都填入后,如果某一宫格内只有一个候选数,那么这个宫格内一定填该数字。
同时别忘了,继续删除同行、同列和同一宫中其他宫格的这个候选数字……
下面简单介绍几种常用的候选数法。
候选数法解题的过程就是逐渐排除不合适的候选数的过程。当某个宫格的候选数排除到只有一个数的时候,那么这个数就是该宫格唯一的一个候选数,这个候选数就是解了。
唯一候选数法应用实例如下。
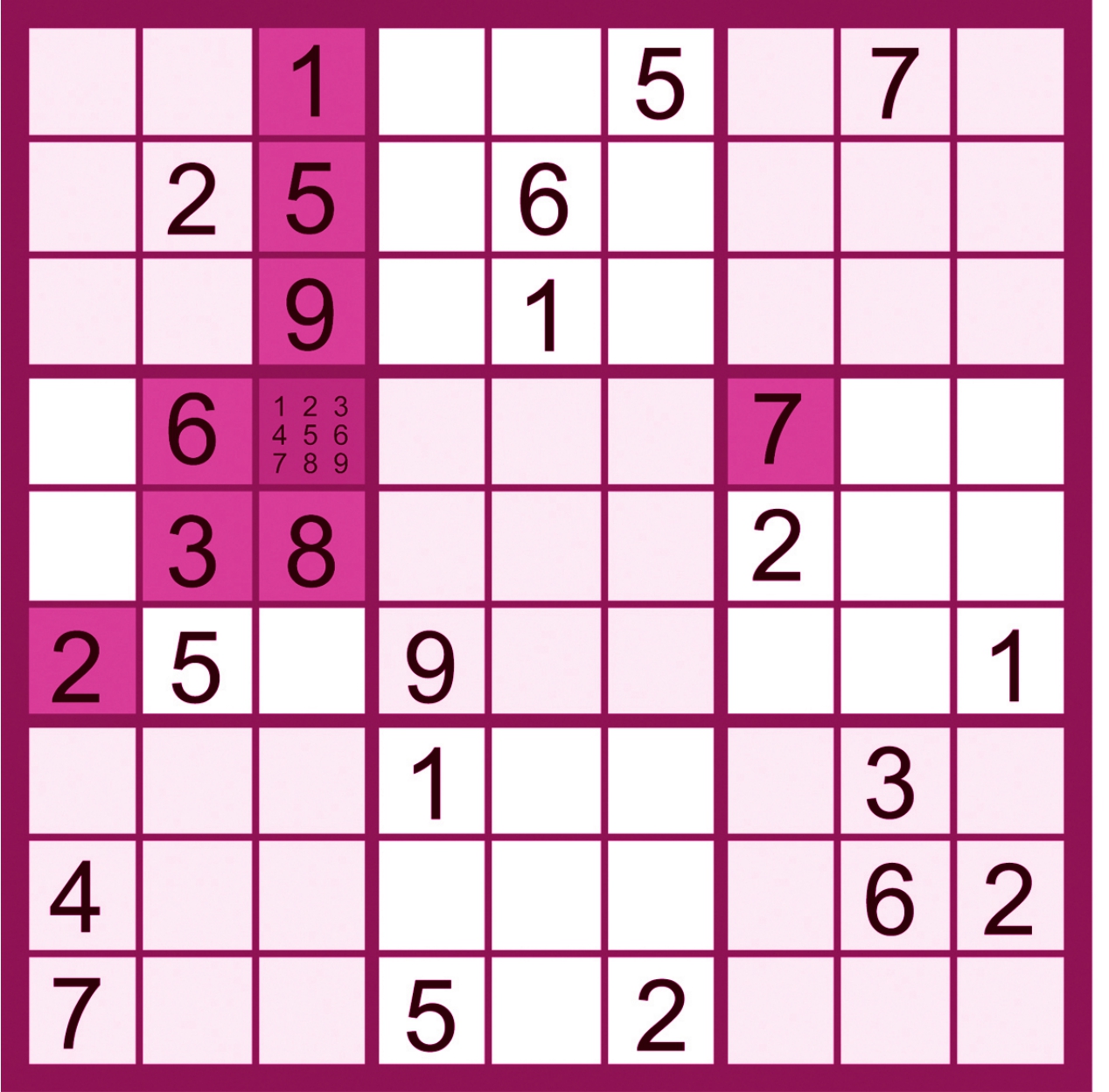
上图中,可以排除(4,3)为1、2、3、5、6、7、8、9的可能,经过候选数的安全删除后,(4,3)中只有4这个唯一的候选数了。
当某个数字在某一行各宫格的候选数中只出现一次时,那么这个数字就是这一列的唯一候选数了,这个宫格的值就可以确定为该数字。这是因为,按照数独游戏的规则要求每一列都应该包含数字1~9,而其他宫格的候选数都不含有该数字,则该数字不可能出现在其他的宫格中,就只能出现在当前宫格中了。对于唯一候选数出现在某一列或九宫格的情况,处理方法完全相同。
隐性唯一候选数法应用实例如下。

上图是制作好的一个候选数表,注意观察(2,5)、(2,9)、(4,1)中的数字。

由上图可以看出在第一列中,数字9只在(4,1)出现;在第五列中,数字3只在(2,5)出现;在第三宫中,数字9只在(2,9)出现。
所以9是第一列的隐性唯一候选数,3是第五列的隐性唯一候选数,9是第三宫的隐性唯一候选数。
所以可以确定:(4,1)=3,(2,5)=3,(2,9)=9。
区块删减法和直观法中的区块摒除法的原理是一样的,通过已知某一区块包含某个数字,可以删减某些宫格的候选数。
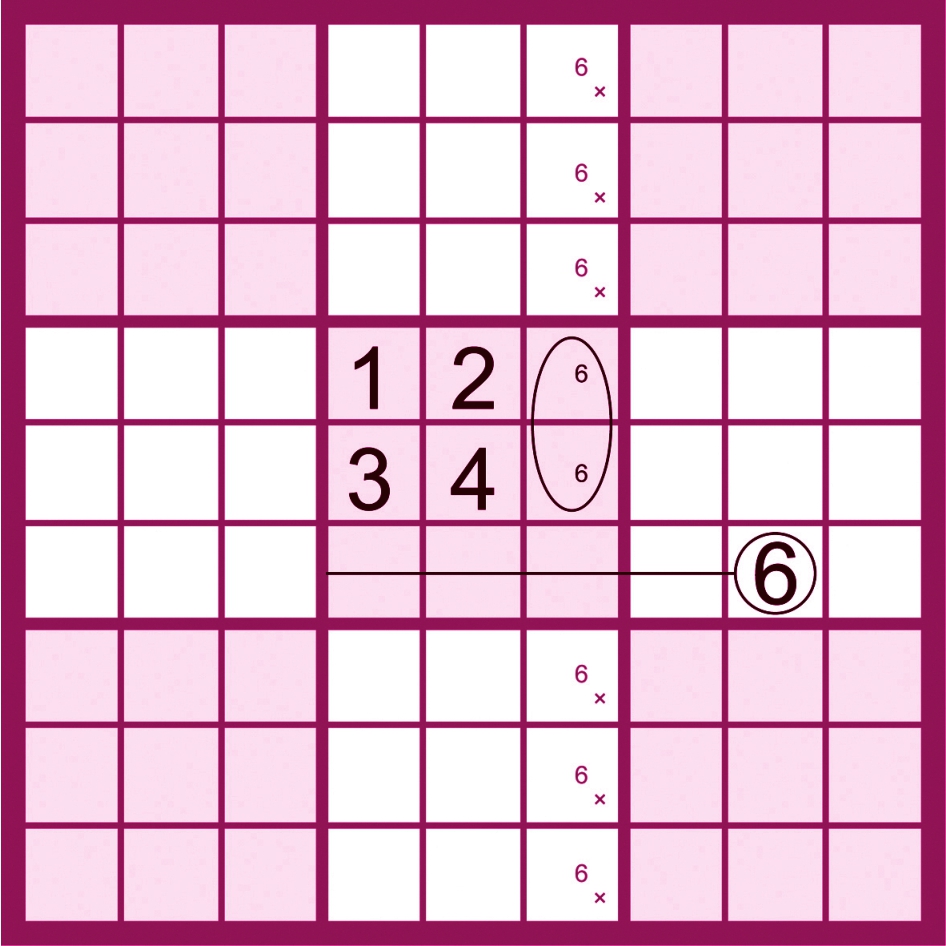
区块删减法应用实例如下。
下图中第五宫内的两个候选数5把同列的其他两宫的5排除了,因为该列的5被锁定在这两格中。
候选数法还有很多技巧,也比较复杂。本书中的题目用直观法都可以解答出来,故这里对候选数法不进行详细叙述,有兴趣的读者可以另外阅读相关资料。
