




我们已经看到,从作用上看,函数也是一类抽象,它们描述了一些对数值的复合操作,但并不依赖具体的数。例如,在声明

时,我们讨论的并不是某个具体数的立方,而是得到任意数的立方的方法。当然,我们也完全可以不声明函数,而总是写出下面这样的表达式:

并不明确地提出cube。但是,这样做将把我们自己置于严重的劣势中,迫使我们始终在语言恰好提供的那一组基本操作(例如这里的乘法)上工作,而不能基于更高级的操作开展工作。我们的程序也能计算立方,但我们的语言却没有表述立方概念的能力。我们对功能强大的程序设计语言有一个必然要求,就是应该能给各种公共模式赋予名字,建立抽象,而后直接在抽象上工作。函数为我们提供了这种能力,这也是为什么除了最简单的程序设计语言外,其他语言都一定包含声明函数的机制的原因。
然而,即使在数值处理领域,如果我们被限制在函数只能以数为参数,也会严重限制我们建立抽象的能力。我们经常能看到同样的程序设计模式被用于描述不同函数的情况。为了把这样的模式描述为概念,我们就需要构造另一类函数,它们以函数作为参数,或者以函数作为返回值。这种操作函数的函数称为 高阶函数 。本节将展示高阶函数如何能够成为一种功能强大的抽象机制,从而极大地增强语言的表达能力。
考虑下面的三个函数,第一个计算从a到b的各个整数之和:

第二个计算给定范围内的各整数的立方和:

第三个计算下面序列里顺序的各项之和:
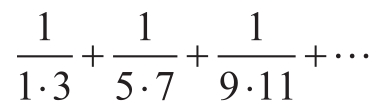
它将(非常缓慢地)收敛到π/8 [11] :

这三个函数很明显共享了一种公共的基础模式,它们中的很大一部分是相同的,只在所用的函数名上互异:用于从a算出所需的求和项的函数,以及用于提供下一个a值的函数。我们可以通过填充同一个模板里的各个空位,生成上面的几个函数:

这种公共模式的存在是很强的证据,说明在这里存在着一种有用的抽象,等待着被提取出来。确实,数学家早就认识到 序列求和 的抽象模式,并发明了“∑记法”,例如:
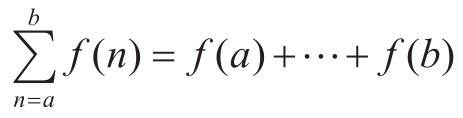
描述了求和的概念。∑记法的威力在于它使数学家能去直接处理求和的概念本身——而不仅是具体的求和——例如,去形式化某些并不依赖于特定求和序列的普适结果。
类似地,作为程序设计者,我们也希望所用的语言足够强大,能用于写出函数去表述求和的概念本身,而不是只能写计算某个具体求和的函数。我们确实可以在我们的语言里做这种事情,为此只要拿来上面的模式,把其中的“空位”翻译为形式参数:

请注意,sum仍然以作为下界和上界的a和b为参数,但又增加了两个函数参数term和next。使用sum的方法正如使用其他函数。例如,我们可以基于它声明sum_cubes(还需要一个函数inc,它得到参数值加一):

利用这个函数,我们也可以算出从1到10的立方和:

利用一个恒等函数来计算项的值,我们就可以基于sum声明函数sum_integers:

然后就可以求从1到10的整数之和了:

我们也可以采用同样的方式声明pi_sum
 :
:

利用这个函数就能计算π的近似值了:

一旦有了sum,我们就能用它作为基本构件,进一步形式化其他概念。例如,求函数 f 在范围 a 和 b 之间的定积分的近似值,可以用下面这个公式完成:
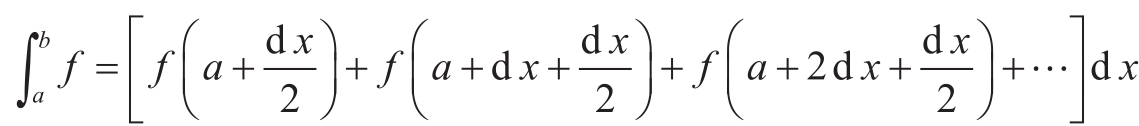
其中,d x 是一个很小的值。我们可以把这个公式直接描述为一个函数:

(cube在0和1间积分的精确值是1/4。)
练习1.29 辛普森规则是另一种数值积分方法,比上面的规则更精确。使用辛普森规则,函数 f 在范围 a 和 b 之间的定积分的近似值是:
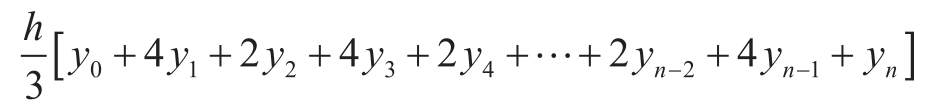
其中的 h =( b-a )/ n , n 是某个偶数,而 y k = f ( a + kh )。(采用较大的 n 能提高近似精度。)请声明一个具有参数 f 、 a 、 b 和 n ,采用辛普森规则计算并返回积分值的函数。用你的函数求cube在0和1之间的积分(取 n =100和 n =1 000),并用得到的值与上面用integral函数得到的结果比较。
练习1.30 上面声明的sum函数将产生一个线性递归。我们可以重写该函数,使之能迭代地执行。请说明应该怎样填充下面声明中空缺的表达式,完成这一工作。

练习1.31
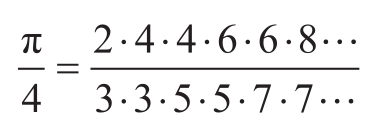
a.函数sum是可以用高阶函数表示的大量类似抽象中最简单的一个
 。请写一个类似的称为product的函数,它返回某个函数在给定范围中各个点上的值的乘积。请说明如何利用product声明factorial。再请根据下面公式计算π的近似值
。请写一个类似的称为product的函数,它返回某个函数在给定范围中各个点上的值的乘积。请说明如何利用product声明factorial。再请根据下面公式计算π的近似值
 :
:
b.如果你的product函数生成的是一个递归计算过程,那么请写一个生成迭代计算过程的函数。如果它生成迭代计算过程,请写一个生成递归计算过程的函数。
练习1.32
a.请说明,sum和product(练习1.31)都是另一个称为accumulate的更一般概念的特殊情况,accumulate使用某些普适的累积函数组合起一系列项:
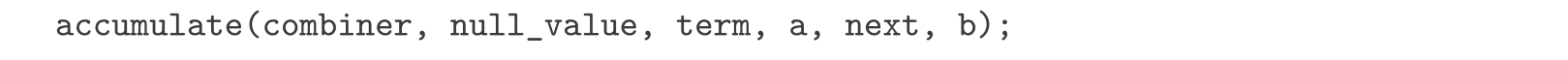
accumulate取与sum和product一样的项和范围描述参数,再加一个(两个参数的)combiner函数,它说明如何组合当前项与前面各项的积累结果,还有一个null_value参数,它说明在所有的项都用完时的基本值。请声明accumulate,并说明我们能怎样通过简单调用accumulate的方式写出sum和product的声明。
b.如果你的accumulate函数生成的是递归计算过程,那么请写一个生成迭代计算过程的函数。如果它生成迭代计算过程,请写一个生成递归计算过程的函数。
练习1.33 你可以引进一个针对被组合项的 过滤器 (filter)概念,写出一个更一般的accumulate(练习1.32)版本,对于从给定范围得到的项,该函数只组合起那些满足特定条件的项。这样就得到了一个filtered_accumulate抽象,其参数与上面的累积函数一样,再增加一个表示所用过滤器的谓词参数。请把filtered_accumulate声明为一个函数,并用下面实例展示如何使用filtered_accumulate:
a.区间 a 到 b 中的所有素数之和(假定你已经有谓词is_prime)。
b.求小于 n 的所有与 n 互素的正整数(即所有满足GCD( i , n )=1的整数 i < n )之乘积。
在1.3.1节使用sum时,我们必须声明一些如pi_term和pi_next的简单函数,用作高阶函数的参数。这种做法看起来不太舒服。如果可以不显式声明pi_term和pi_next,而是有一种方法,使我们能直接描述“那个返回其输入值加4的函数”和“那个返回其输入与它加2的乘积的倒数的函数”,那就更方便了。引入lambda 表达式 作为创建函数的语法形式,就能做好这件事。利用lambda表达式,我们能如下描述这两个函数:

和

这样就可以无须声明任何辅助函数,直接写pi_sum函数了:

借助lambda表达式,我们也可以写integral函数而不需要声明辅助函数add_dx:


一般而言,lambda表达式采用与函数声明类似的形式创建函数,但不需要为被创建的函数提供名字,也不需要用关键字return和花括号(如果只有一个参数,围绕着参数列表的圆括号也可以略去,就像在上面看到的那样)
 :
:

这样得到的函数与通过函数声明语句创建的函数一样,仅有的不同之处,就是这种函数没有在环境中被关联于任何名字。考虑

它等价于


我们可以按如下方式读一个lambda表达式:

就像任何以函数为值的表达式一样,lambda表达式也能用作组合式的运算符,例如:
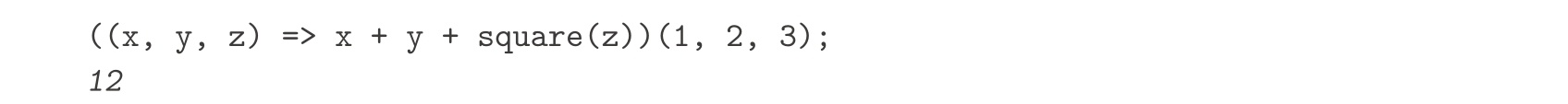
或者更一般地,将其用在任何通常使用函数名的上下文中
 。请注意,=>的优先级比函数应用更低,因此这里围绕着lambda表达式的括号是必需的。
。请注意,=>的优先级比函数应用更低,因此这里围绕着lambda表达式的括号是必需的。
用const创建局部名字
lambda表达式的另一应用是用于创建局部的名字。在函数里,除了可以使用已经约束为函数参数的名字外,我们也经常需要其他局部名。例如,假设我们希望计算:
f ( x , y )= x (1+ xy ) 2 + y (1 -y )+(1+ xy )(1 -y )
我们可以将其表述为:
a =1+ xy
b =1 -y
f ( x , y )= xa 2 + yb + ab
在写计算 f 的函数时,我们希望包含的局部名字可能不止 x 和 y ,还有表示中间值的名字如 a 和 b 。做这件事的一种方法是用一个辅助函数来约束局部的名字:

换种方式,我们也可以用一个lambda表达式描述建立约束的局部名字的匿名函数。这样,整个函数体就变成了一个对该函数的简单调用:
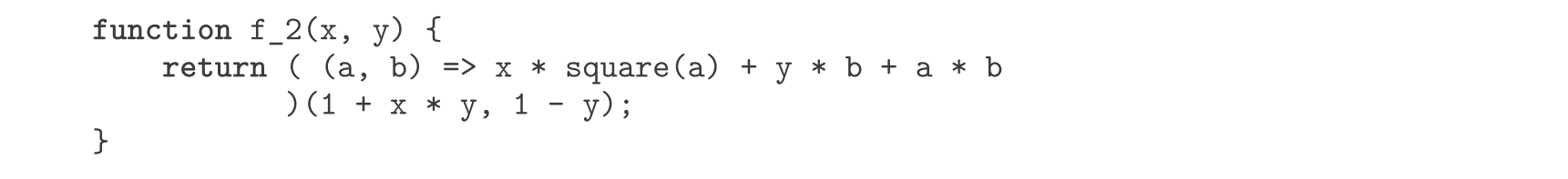
更方便的声明局部名字的方法,是在函数体里使用常量声明。利用const语句,前面的函数可以写成:

在一个块里用const声明的名字,总以包围该声明的最小块作为作用域
[12]
,
 。
。
条件语句
我们已经看到,声明一些局部于函数声明的名字很有用。当函数变得更大时,我们应该把名字的作用域维持得尽可能小。考虑练习1.26里的示例expmod:

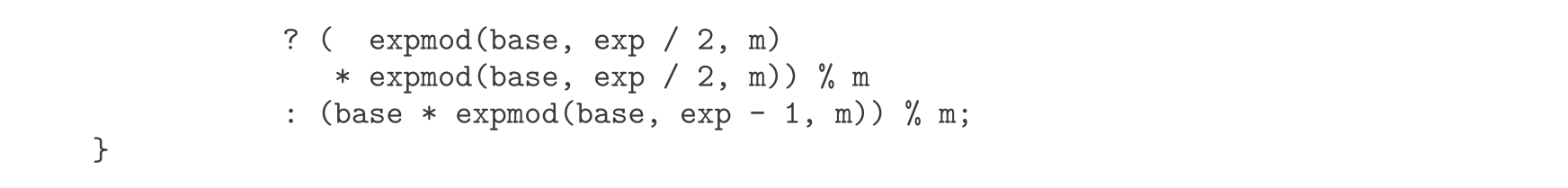
这个函数包含了两个如下的函数调用,由此造成的效率损失毫无必要:

虽然对这个例子,我们可以用一个square函数简单地修复问题,但一般情况不会都这么容易。不用square,我们也可能想到为这个表达式引进一个局部名字,例如写:

但这样做不但使程序低效,实际上还会使它不终止了!问题是常量声明出现在条件表达式之外,这就意味着它总要执行,包括对exp===0的基础情况。为避免这种问题,这里应该用 条件语句 ,把返回语句放在其分支里。利用条件语句,我们可以声明expmod函数如下:

条件语句的一般形式是:
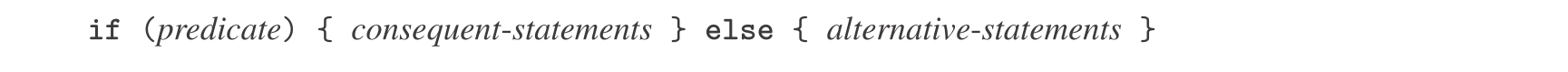
与条件表达式类似,解释器也是先求值 predicate 。如果这个求值得到真,解释器就去求值 consequence-statements (后继语句);而如果求值得到假,解释器就去求值 alternative-statements (替代语句)。这里对返回语句求值导致退出外围的函数体,序列中位于返回语句之后的语句以及条件语句之后的语句都直接忽略。注意,出现在条件语句的两个块之一里有一个常量声明,它也局部于相应的块。一对花括号围起的部分构成了一个块。
练习1.34 假设我们声明了

而后我们写

如果我们(坚持)要求解释器求值f(f),会发生什么情况呢?请给出解释。
在1.1.4节,我们介绍了复合函数的机制,它能作为用于抽象数值运算的模式的机制,使描述的计算不依赖具体的数值。有了高阶函数,例如1.3.1节介绍的integral函数,我们初步看到了另一种威力更强大的抽象函数,它们可以用于描述通用的计算方法,并不依赖于其中涉及的具体函数。本节将讨论两个更复杂的例子——找函数的零点和不动点的通用方法——用以展示我们能如何使用函数去直接描述这一类方法。
通过区间折半方法找方程的根
区间折半方法 是求方程 f ( x )=0的根的一种简单但又威力强大的方法,这里的 f 是一个连续函数。折半方法的基本思想如下:如果对给定的点 a 和 b 有 f ( a )< 0 < f ( b ),那么 f 在 a 和 b 之间必然有一个零点。为了确定这个零点,我们令 x 是 a 和 b 的平均值并计算出 f ( x )。如果 f ( x )> 0,那么在 a 和 x 之间必然有 f 的一个零点;如果 f ( x )< 0,那么在 x 和 b 之间必然有 f 的一个零点。继续按这种方法做下去,我们就能确定一串越来越小的区间,而且保证在每个区间里必然有 f 的一个零点。到某个时刻,此时的区间已经足够小,就可以结束这个计算过程了。因为区间在计算过程中的每一步缩小一半,所以计算所需最大步数的增长将是 Θ (log( L / T )),其中的 L 是初始区间的长度, T 是可容忍的误差(也就是说,认为已经“足够小”的区间的大小)。下面是一个实现了这一策略的函数:

我们假定计算开始时给定了函数
f
以及使其取值为负和正的两个点。我们首先算出这两个给定点的中点,而后检查给定区间是否已经足够小。如果是,就返回这个中点的值作为回答;否则就算出
f
在这个中点的值。如果检查发现算出的值为正,那么就以从原来的负端点到中点为新区间并继续;如果值为负,就以从中点到原来为正的端点为新区间并继续。还有,也存在检测值恰好为0的可能,这时中点就是我们寻找的根。为了检查两个端点是否已经“足够小”,我们可以采用类似1.1.7节中计算平方根时所用的那种函数
 :
:

直接使用search函数有些麻烦,因为我们可能会偶然给了它一对点,相应的
f
值并不具有这个函数所需要的正负号,这时就会得到错误的结果。我们可以换一种方式,通过下面的函数去使用search。该函数首先检查给定端点中是否具有负的函数值,而另一个点是正值,然后根据具体情况去调用search函数。如果函数发现两个给定点的函数值同号,折半方法无法工作,就发出一个表示出错的信号
 。
。

下面的实例用折半方法求出sin x =0在2和4之间的根,得到的是π的近似值:

这里是另一个例子,用折半方法求出 x 3 -2 x -3=0在1和2之间的根:
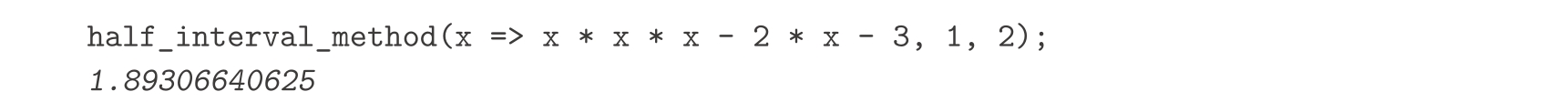
寻找函数的不动点
数 x 称为函数 f 的 不动点 ,如果 x 满足方程 f ( x )= x 。对于一些函数,通过从某个初始猜测出发,反复应用 f ,
f ( x ), f ( f ( x )), f ( f ( f ( x ))),…
直到值的变化不太大时,我们就定位到函数 f 的一个不动点。利用这一想法,我们可以设计一个函数fixed_point,它以一个函数和一个初始猜测为参数,产生该函数的一个不动点的近似值。我们反复应用这个函数,直到发现连续两个值之差小于某个事先给定的容许值:

例如,我们可以用这个方法逼近余弦函数的不动点,其中用1作为初始近似值
 :
:

类似地,我们也可以用下面方法寻找方程 y =sin y +cos y 的解:
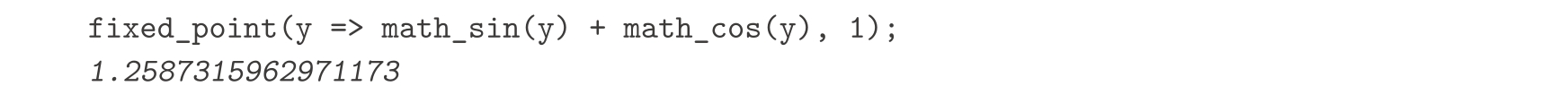
这种不动点计算过程,可能使人想起1.1.7节里求平方根的计算过程。两者都基于反复改进一个猜测值,直到结果满足某个评价准则为止。事实上,我们完全可以把平方根计算形式化为一个寻找不动点的计算过程。计算某个数 x 的平方根,就是要找到一个 y 使得 y 2 = x 。我们把这个等式改成另一等价形式 y = x / y ,可以看到,这里要做的就是寻找函数 y ↦ x / y 的不动点 [13] 。因此,我们可以试着用下面的方法计算平方根:

不幸的是,这一不动点搜寻的过程不收敛。考虑某个初始猜测 y 1 ,下一个猜测将会是 y 2 = x / y 1 ,而再下一个猜测就是 y 3 = x / y 2 = x /( x / y 1 )= y 1 。结果就是无穷循环,其中没完没了地反复出现两个猜测 y 1 和 y 2 ,在答案的两边往复振荡。
控制这类振荡的一种想法是设法避免猜测的变化过于剧烈。因为实际答案一定在两个猜测 y 和 x / y 之间,我们可以做一个猜测,使之不像 x / y 那样远离 y ,为此可以考虑用 y 和 x / y 的平均值。这样, y 之后的猜测值就取(1/2)( y + x / y )而不是 x / y 。做出这种猜测序列的计算过程,也就是搜寻 y ↦(1/2)( y + x / y )的不动点:
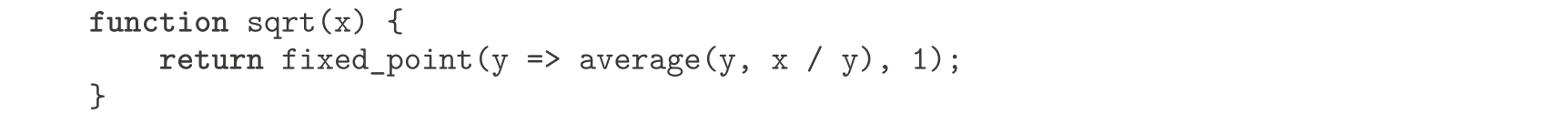
(请注意, y =(1/2)( y + x / y )是方程 y = x / y 经过简单变换的结果,推导出它的方法是在方程的两边都加 y ,然后再将两边都除以2。)
经过上述修改,这个平方根函数就能正常工作了。事实上,如果拆解这个定义,我们就会看到它在求平方根时产生的近似值序列,正好就是1.1.7节里的那个求平方根函数产生的序列。这种在逼近一个解的过程中,取用一些序列值的平均值的技术称为 均值阻尼 ,这种技术常常被用在不动点搜寻中,作为帮助收敛的手段。
练习1.35 请证明黄金分割率ϕ(1.2.2节)是变换 x ↦1+1/ x 不动点。请利用这一事实,通过函数fixed_point计算ϕ的值。
练习1.36 请修改fixed_point,使它能用练习1.22介绍的基本函数newline和display打印出计算中产生的近似值序列。然后,通过找 x ↦log(1000)/log( x )不动点的方法确定 x x =1000的一个根(请利用JavaScript的基本函数math_log,它计算参数的自然对数值)。请比较一下采用均值阻尼和不用均值阻尼时的计算步数。(注意,你不能用猜测1去启动fixed_point,因为这将导致除以log(1)=0。)
练习1.37 无穷连分式是具有如下形式的表达式:
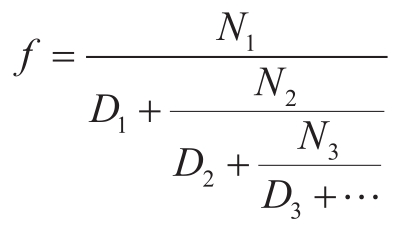
作为例子,我们可以证明当所有的 N i 和 D i 都等于1时,这个无穷连分式的值是1/ϕ,其中的 ϕ 就是黄金分割率(见1.2.2节的说明)。逼近给定无穷连分式的一种方法是在给定数目的项之后截断,这样的截断式称为 k 项的有限连分式 ,其形式是:
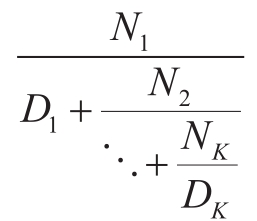
a.假定n和d都是只有一个参数(项的下标 i )的函数,它们分别返回连分式的项 N i 和 D i 。请声明一个函数cont_frac,使得对cont_frac(n,_d,_k)的求值计算 k 项有限连分式的值。通过如下调用检查你的函数对顺序的k值是否逼近1/ ϕ :

你需要取多大的k才能保证得到的近似值具有十进制的4位精度?
b.如果你的cont_frac函数产生递归计算过程,那么请另写一个产生迭代计算的函数。如果它产生迭代计算,请另写一个函数,使之产生一个递归计算过程。
练习1.38 1737年瑞士数学家莱昂哈·德欧拉发表了论文 De Fractionibus Continuis ,文中给出了e-2的一个连分式展开,其中e是自然对数的底。在这一连分式中, N i 全都是1,而 D i 顺序的是1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8,…。请写一个程序,其中使用你在练习1.37中做的cont_frac函数,该程序基于欧拉的展开计算e的近似值。
练习1.39 1770年,德国数学家J.H.Lambert发表了正切函数的连分式表示:
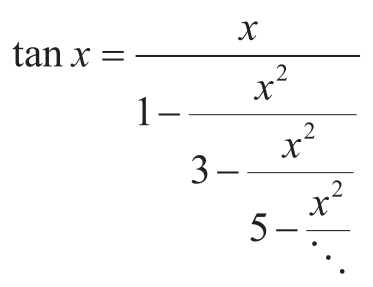
其中 x 用弧度表示。请声明一个函数tan_cf(x,_k),它基于Lambert公式计算正切函数的近似值。k描述计算的项数,就像练习1.37一样。
上面的例子说明,允许把函数作为参数传递,能显著增强我们的程序设计语言的表达能力。如果能创建其返回值本身也是函数的函数,我们还能得到进一步的表达能力提升。
我们用例子说明这一思想,还是用1.3.3节最后介绍的不动点的例子。在那里,我们构造了一个平方根程序的新版本,其中把这项计算看作一种不动点搜寻。开始时,我们注意到
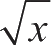 就是函数
y
↦
x
/
y
的不动点,后来利用均值阻尼使这一逼近能够收敛。均值阻尼本身也是一种很有用的通用技术。对于给定的函数
f
,均值阻尼考虑的是另一个函数,它在
x
处的值等于
x
和
f
(
x
)的平均值。
就是函数
y
↦
x
/
y
的不动点,后来利用均值阻尼使这一逼近能够收敛。均值阻尼本身也是一种很有用的通用技术。对于给定的函数
f
,均值阻尼考虑的是另一个函数,它在
x
处的值等于
x
和
f
(
x
)的平均值。
我们可以把均值阻尼的想法表述为下面的函数:

函数average_damp的参数是函数f,它返回另一个函数作为值(用lambda表达式生成),当我们把这个返回值函数应用于数x时,得到的就是x和f(x)的平均值。例如,把函数average_damp应用于square函数,就能生成另一个函数,该函数在数值
x
处的值是
x
和
x
2
的平均值。把这样得到的函数应用于10,返回的是10与100的平均值55
 :
:

利用average_damp,我们可以重做前面的平方根函数如下:
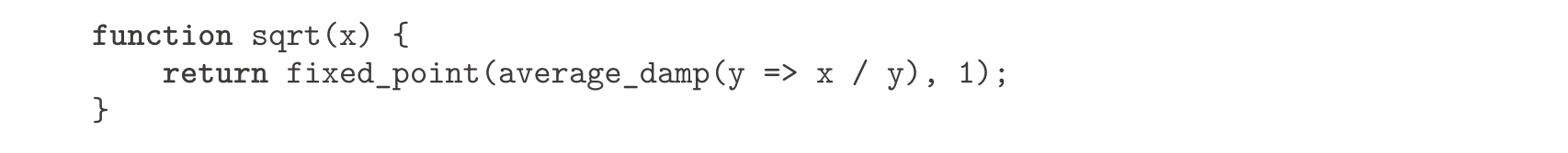
请注意看上面的函数,看这里怎样明确地结合了三种思想(不动点搜寻、均值阻尼以及函数
y
↦
x
/
y
)。比较一下这个平方根计算函数与1.1.7节给出的原始本也很有教益。请记住,这两个函数描述了同一个计算过程,还请注意,当我们利用上面的抽象描述该计算过程时,其中的思想如何变得更清晰了。一般而言,把一个计算过程形式化地表述为一个函数,可能存在多种不同方法。有经验的程序员知道如何选择函数的形式,使其特别清晰并容易理解,也使该计算过程中的有用元素能表现为一些相互独立的个体,从而使它们还可能重用于其他应用。作为重用的一个简单实例,请注意
x
的立方根是函数
y
↦
x
/
y
2
的不动点,因此我们立刻就可以把前面的平方根函数修改成一个计算立方根的函数
 :
:
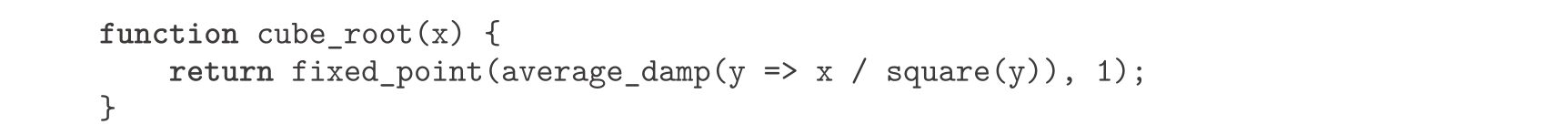
牛顿法
在1.1.7节介绍平方根函数时,我们曾经说过,该函数是更一般的 牛顿法 的一个特殊情况。如果 x ↦ g ( x )是一个可微函数,那么方程 g ( x )=0的一个解就是函数 x ↦ f ( x )的一个不动点,其中:
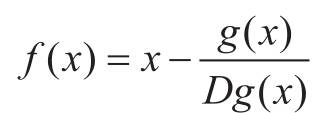
这里的
Dg
(
x
)是
g
的导数在
x
处的值。牛顿法就是使用我们前面看到的不动点方法,通过搜寻函数
f
的不动点的方法,去逼近上面方程的解
[14]
。对于许多函数以及充分好的初始猜测
x
,牛顿法能很快收敛到
g
(
x
)=0的一个解
 。
。
为了把牛顿法实现为函数,我们必须首先描述求导的思想。请注意,“导数”与均值阻尼类似,也是从一个函数到另一个函数的变换。例如,函数 x ↦ x 3 的导数是函数 x ↦3 x 2 。一般而言,如果 g 是一个函数而d x 是一个很小的数,那么 g 的导数在任意值 x 的值由下面的函数(作为小数d x 的极限)给出:
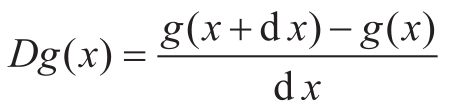
这样,我们就可以用下面这个函数描述求导数的思想(例如,取d x 为0.000 01):

再加上声明:

与average_damp类似,deriv也是一个以函数为参数,返回一个函数作为值的函数。例如,为了求函数 x ↦ x 3 的导数在5的近似值(精确值为75),我们求值:

有了deriv的帮助,我们就能把牛顿法表述为一个求不动点的计算过程了:

newton_transform函数描述的就是本节开始给出的公式,基于它声明newtons_method已经很容易了。这个函数以一个函数为参数,它计算的就是我们希望找到零点的函数,这里还需要给一个初始猜测。例如,为确定
x
的平方根,可以用初始猜测1,通过牛顿法去找函数
y
↦
y
2
-x
的零点
 。这样就给出了求平方根函数的另一种形式:
。这样就给出了求平方根函数的另一种形式:
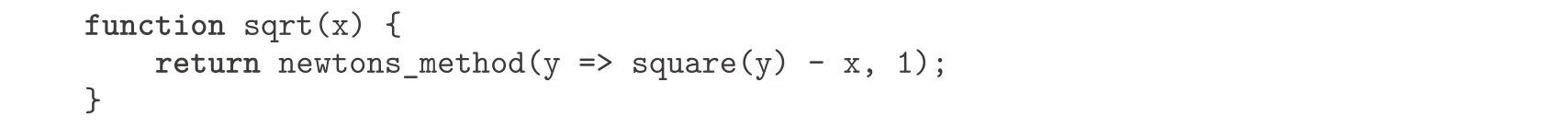
抽象和一等函数
我们在上面已经看到了两种不同的方法,它们都能把平方根计算表述为某种更一般的方法的实例。其一是作为一个搜寻不动点的函数,另一个使用牛顿法。因为牛顿法本身也表述了一个不动点的计算过程,所以,实际上我们看到的是作为不动点来计算平方根的两种不同形式。每种方法都是从一个函数出发,找出这一函数在某种变换下的不动点。我们也可以把这一具有普适意义的思想本身表述为一个函数:

这是一个非常普适的函数,其参数包括一个函数参数g(它计算的某个函数),还有一个对g做变换的函数和一个初始猜测,它返回的是通过变换得到的那个函数的不动点。
利用这一抽象,我们可以重新描述本节的第一个平方根计算(搜寻 y ↦ x / y 在均值阻尼下的不动点),把它作为上述普适方法的实例:

类似地,我们也可以把本节的第二个平方根计算(它也是牛顿法的一个实例,设法找到牛顿变换 y ↦ y 2 -x 的不动点)重述为:

从1.3节开始,我们看到复合函数是一种至关重要的抽象机制,它使我们能把通用的计算方法明确描述为我们的程序设计语言的元素。现在我们又看到,高阶函数使我们能怎样去操控这些通用的方法,建立进一步的抽象。
作为编程者,我们应该对识别程序中的各种基本抽象的可能性保持高度敏感,设法去构造它们,进而设法去推广它们,创建威力更强大的抽象。当然,这并不是说总应该用尽可能最抽象的方式去写程序。程序设计专家知道如何根据面临的工作选择合适的抽象层次。但是,能基于这些抽象思考是最重要的,只有这样,我们才可能在新的上下文中应用它们。高阶函数的重要性,就在于使我们能用程序设计语言的元素明确地描述这些抽象,并使它们能像其他计算元素一样作为被操作的对象。
一般而言,对于各种计算元素的可能使用方式,程序设计语言都会设置一些限制。限制最少的元素称为具有
一等
的地位。一等元素的某些“权利或特权”包括
 :
:
●它们可以命名;
●它们可以作为实参提供给函数;
●它们可以由函数作为结果返回;
●它们可以被包含在数据结构中
 。
。
JavaScript与其他一些高级程序设计语言一样,给了函数完全的一等地位。这些也给有效实现提出了挑战,但由此获得的描述能力却是极其惊人的
 。
。
练习1.40 请声明一个函数cubic,它可以和newtons_method函数一起用在下面的形式的表达式里:

以逼近三次方程 x 3 + ax 2 + bx + c 的零点。
练习1.41 请声明一个函数double,它以一个只有一个参数的函数为参数,返回另一个函数,后一函数将连续地应用原来的那个参数函数两次。例如,如果inc是一个给参数加1的函数,double(inc)将给参数加2。下面这个语句返回什么值:

练习1.42 令 f 和 g 是两个单参数的函数, f 在 g 之后的 复合 定义为函数 x ↦ f ( g ( x ))。请声明一个函数compose实现函数复合。例如,如果inc是将参数加1的函数,那么就有:

练习1.43 如果 f 是一个数值函数, n 是一个正整数,我们可以构造 f 的 n 次重复应用,也就是说,这个函数在 x 的值应该是 f ( f (…( f ( x ))…))。举例说,如果 f 是函数 x ↦ x +1, n 次重复应用 f 就是函数 x ↦ x + n 。如果 f 是求数的平方的函数, n 次重复应用 f 就求出其参数的2 n 次幂。请写一个函数,其输入是一个计算 f 的函数和一个正整数 n ,返回的是计算 f 的 n 次重复应用的那个函数。你的函数应该能以如下方式使用:

提示:你可能发现,利用练习1.42的compose可能带来一些方便。
练习1.44 平滑 一个函数的思想是信号处理中的一个重要概念。如果 f 是函数,d x 是某个很小的数值,那么 f 的平滑版本也是函数,它在点 x 的值就是 f ( x -d x )、 f ( x )和 f ( x +d x )的平均值。请写一个函数smooth,其参数是一个计算 f 的函数,返回 f 经过平滑后的那个函数。有时我们可能发现,重复地平滑一个函数,得到经过 n 次平滑的函数(也就是说,对平滑后的函数再做平滑,等等)也很有价值。请说明怎样利用smooth和练习1.43的repeated,构造出能对给定的函数做 n 次平滑的函数。
练习1.45 我们在1.3.3节看到,用朴素方法通过找 y ↦ x / y 的不动点来计算平方根的方法不收敛,但可以通过均值阻尼的技术弥补。同样的技术也可以用于计算立方根,将其看作均值阻尼后的 y ↦ x / y 2 的不动点。不幸的是,这个方法对四次方根行不通,一次均值阻尼不足以使对 y ↦ x / y 3 的不动点搜寻收敛。然而,如果我们求两次均值阻尼(即用 y ↦ x / y 3 均值阻尼的均值阻尼),这一不动点搜寻就收敛了。请做些试验,考虑把计算 n 次方根作为基于 y ↦ x / y n -1 的反复做均值阻尼的不动点搜寻过程,请设法确定各种情况下需要做多少次均值阻尼,并基于这一认识实现一个函数,它能利用fixed_point、average_damp和练习1.43的repeated函数计算 n 次方根。假定你需要的所有算术运算都是基本函数。
练习1.46 本章描述的一些数值算法都是 迭代式改进 的实例。迭代式改进是一种非常通用的计算策略,它说:为了计算某些东西,我们可以从对答案的某个初始猜测开始,检查这一猜测是否足够好,如果不行就改进这一猜测,将改进后的猜测作为新猜测继续这一计算过程。请写一个函数iterative_improve,它以两个函数为参数:其中一个表示评判猜测是否足够好的方法,另一个表示改进猜测的方法。iterative_improve的返回值应该是函数,它以某个猜测为参数,通过不断改进,直至得到的猜测足够好为止。利用iterative_improve重写1.1.7节的sqrt函数和1.3.3节的fixed_point函数。
[1] 在本书中说明表达式的语法形式时,我们将用斜体字符(例如 name )表示表达式中的一些“空位置”。在实际写这种表达式时,需要填充这些空位。
[2] 完全版本的JavaScript条件表达式允许求值 predicate 表达式得到任意结果,而不仅是布尔值(细节见4.1.3节的脚注14)。本书中的条件表达式只使用了具有布尔值的谓词表达式。
[3] 在实际程序里,我们可能会采用上一节介绍的块结构,把fact_iter的声明隐藏起来:

上面没有这样做,是因为不希望增加需要同时考虑的事项。
[4] 帕斯卡三角形的元素又称二项式系数,因为其中第 n 行就是( x + y ) n 的展开式的系数。采用该模式计算这些系数的工作发表在布赖斯·帕斯卡1653年有关概率论的开创性论文“论算术三角形”( Traité du triangle arithmétique )中。根据Edwards(2019)的说法,同样的模式也出现在11世纪波斯数学家Al-Karaji的著作中,还出现在12世纪印度数学家Bhaskara和13世纪中国数学家杨辉的著作中。[这个三角形也称为“贾宪三角形”(贾宪,宋朝人,远早于帕斯卡)或“杨辉三角形”,是中国古代数学的重要成就。——译者注]
[5] 更准确地说,这里所需乘法的次数等于 n 的以2为底的对数值,再加上 n 的二进制表示中1的个数减1。这个值总是小于 n 的以2为底的对数值的两倍。对于对数的计算过程,在阶数记法定义中的任意常量 k 1 和 k 2 ,意味着结果与对数的底无关。因此这种过程通常直接描述为 Θ (log n )。
[6] 这一迭代算法也是一个老古董,它出现在公元前200年之前Áchárya Pingala所写的 Chandah-sutra 里。有关求幂的这一算法和其他算法的完整讨论和分析,请参看Knuth 1997b的4.6.3节。
[7] 这一算法称为欧几里得算法,是因为它出现在欧几里得的《几何原本》( Elements ,第7卷,大约为公元前300年)中。根据Knuth(1997a)的看法,这一算法应该被认为是最古老的非平凡算法。古埃及的乘方法(练习1.18)确实年代更久远,但按Knuth的看法,欧几里得算法是已知的最早描述为通用算法的东西,而不是仅仅给出一集示例。
[8] 这一定理是1845年由Gabriel Lamé证明的。Gabriel Lamé是法国数学家和工程师,人们知道他主要是由于他在数学物理领域的贡献。为了证明这一定理,我们考虑数对序列( a k , b k ),其中 a k ≥ b k ,假设欧几里得算法在第 k 步结束。这一证明基于下述论断:如果( a k+ 1 , b k+ 1 )→( a k , b k )→( a k -1 , b k -1 )是归约序列中连续的三个数对,那就必然有 b k +1 ≥ b k + b k -1 。为验证这一论断,应注意这里的每个归约步都是应用变换 a k -1 = b k , b k -1 = a k 除以 b k 的余数。第二个等式意味着 a k = qb k + b k -1 ,其中的 q 是某个正整数。因为 q 至少是1,所以我们有 a k = qb k + b k -1 ≥ b k + b k -1 。但在前一个归约步中有 b k +1 = a k ,因此 b k +1 = a k ≥ b k + b k -1 。这样就证明了上述论断。现在可以通过对 k 归纳证明定理了,设 k 是算法结束所需的步数。对 k =1结论成立,因为在这里也就是要求 b 不小于Fib(1)=1。现在假定结论对所有小于等于 k 的整数成立,我们设法建立对 k +1的结果。令( a k +1 , b k +1 )→( a k , b k )→( a k -1 , b k -1 )是归约过程中连续的几个数对,我们有 b k -1 ≥Fib( k -1)以及 b k ≥Fib( k )。这样,应用上面已证明的论断,再根据Fibonacci数的定义,就可以给出 b k +1 ≥ b k + b k -1 ≥Fib( k )+Fib( k -1)=Fib( k +1)。这就完成了Lamé定理的证明。
[9]
如果
d
是
n
的因子,那么
n/d
当然也是。而
d
和
n/d
绝不会都大于
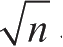 。
。
[10] 对指数值 e 大于1的情况,这里用的归约方法基于如下事实:对任意的 x 、 y 和 m ,我们通过分别计算 x 取模 m 和 y 取模 m ,而后将它们乘起来之后取模 m ,总可以得到 x 乘 y 取模的余数。例如,在 e 是偶数时,我们计算 b e /2 取模 m 的余数,再求出它的平方,而后再求出它取模 m 的余数。这种技术非常有用,因为这意味着计算中不需要处理比 m 大很多的数(请与练习1.25比较)。
[11]
这一序列常写成另一种等价形式:
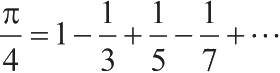 。这一写法归功于莱布尼茨。我们将在3.5.3节看到如何用它作为某些数值技巧的基础。
。这一写法归功于莱布尼茨。我们将在3.5.3节看到如何用它作为某些数值技巧的基础。
[12] 注意,在一个块里声明的名字,在该声明被完全求值前不能用,无论外围块里是否声明了同一个名字。例如,下面程序企图用最高层声明的a为f里声明的b的计算提供值,这样做是行不通的:

这个程序会报错,因为a+x里的a是在a的声明被求值之前使用的。我们将在4.1.6节回到这个程序,那时我们已经学习了更多有关求值的知识。
[13] ↦(读作“映射到”)是数学家写lambda表达式的方法, y ↦ x / y 的意思就是y_=>_x_/_y,也就是那个在 y 处的值为 x / y 的函数。
[14] 基础微积分书籍中通常把牛顿法描述为逼近序列 x n +1 = x n -g ( x n )/ Dg ( x n )。有了能描述计算过程的语言,采用不动点的思想,这一方法的描述也得到了简化。