




(1)问题描述及假设
需求可拆分车辆路径问题(SDVRP)是指:配送网络中有一系列客户点 j ∈{1,2,…, n }及相应需求量( d j ),每个客户点的需求允许分批满足,如何安排一个车队的运输路径访问这些客户点,在满足车辆最大装载量等约束条件下,使得总运输成本最小。SDVRP示意图如图2.3所示。
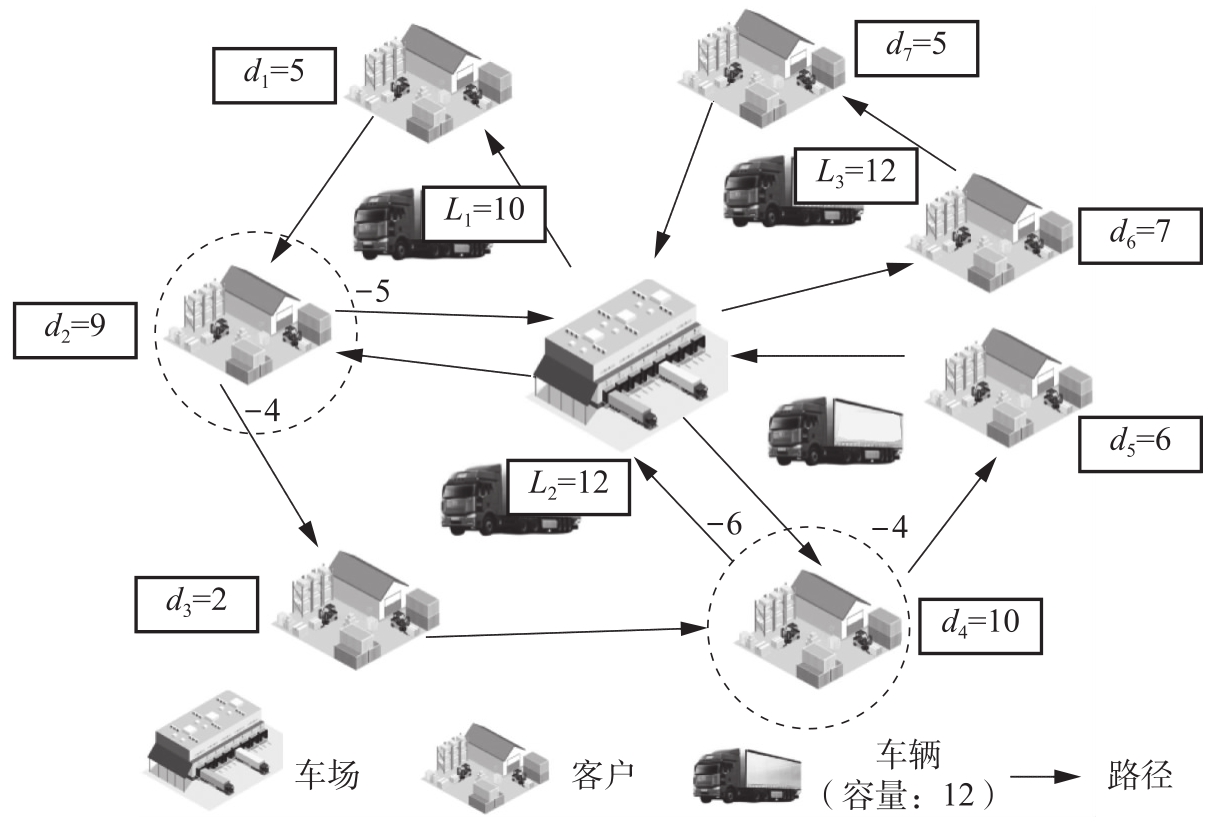
图2.3 SDVRP示意图
该问题研究一般考虑的假设如下:
①所有车辆同质,即具有相同的最大装载量、最大工作时间和车速。
②车辆从配送中心出发,完成任务后返回配送中心。
③每个客户被同一辆车最多访问一次。
④在每个客户点的投货时间忽略不计。
(2)数学模型
模型中的参数和变量如表2.3所示。
表2.3 模型中的符号及解释
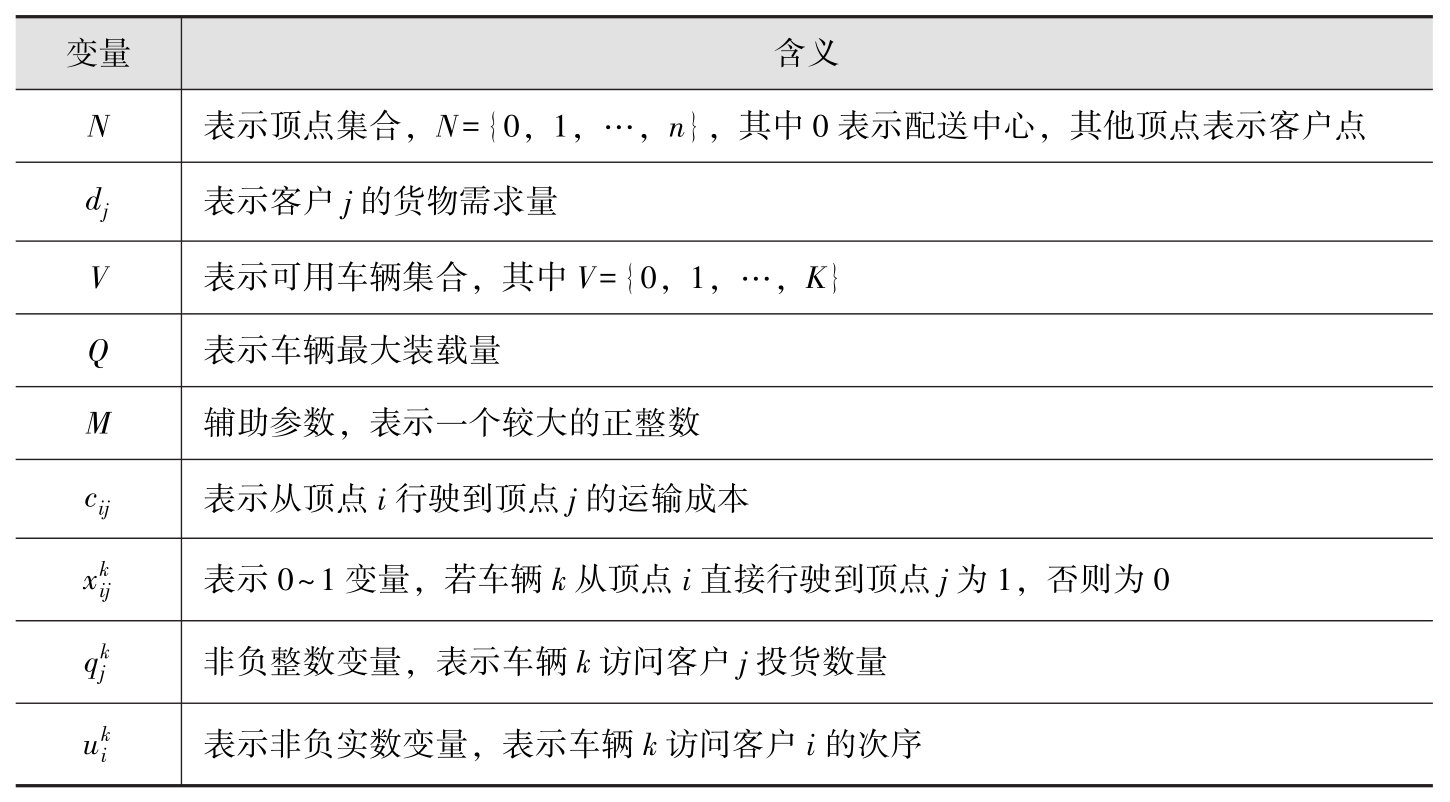
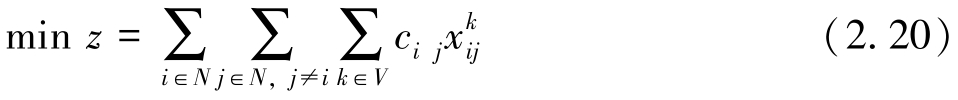


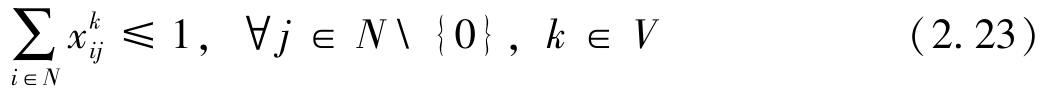
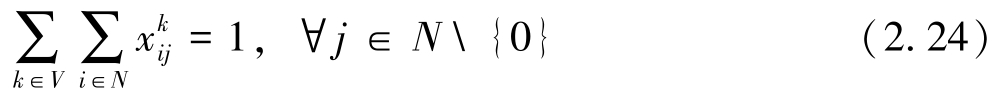
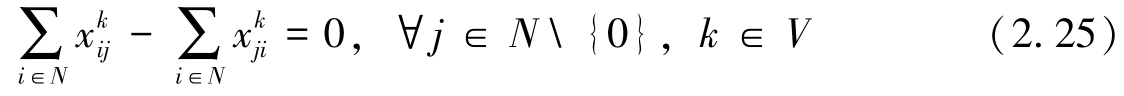

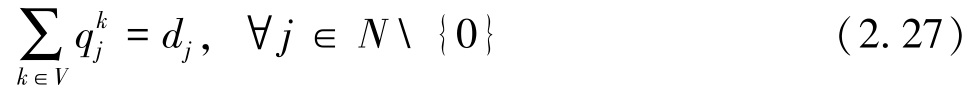
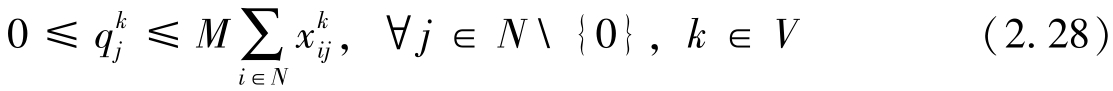
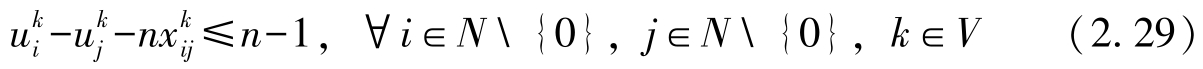
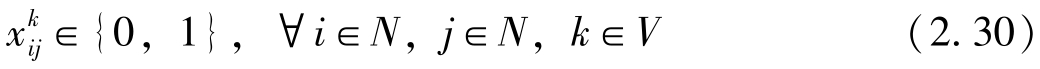

式(2.20)表示目标函数,最小化运输成本。式(2.21)和式(2.22)表示派出车辆从配送中心出发,完成任务后返回配送中心。式(2.23)表示每个客户点被每辆车最多访问一次。式(2.24)表示每个客户点被所有车辆有且仅被访问一次。式(2.25)表示车辆流平衡约束。式(2.26)表示车辆访问所有客户的装载量不能超过其最大允许装载量。式(2.27)表示每个客户的投货需求得到充分满足。式(2.28)表示投放量决策和路径决策之间的关系。式(2.29)表示子回路消除约束。式(2.30)表示0~1路径决策变量。式(2.31)表示客户访问次数决策变量。
(3)求解算法
Archetti等(2006)首次提出了禁忌搜索算法求解该问题。Chen等(2007)提出一种混合启发式算法,其初始解由求解VRP的CW节约算法给出,并使用一种端点整数规划模型对当前解各线路端点进行最优再分配。Marcos等(2015)基于多起点迭代局部搜索设计启发式算法,通过对文献中可用的基准实例进行计算实验。熊浩等(2015)构建了双层规划数学模型并在此思路下设计了三阶段启发式算法:第一阶段不考虑容量限制和拆分需求,给出包括车场和所有顾客的TSP大路径;第二阶段进行切割,同时考虑是否拆分以满足容量限制;第三阶段对第二阶段的子路径进行路径优化调整。同时,Silva等(2015)提出了迭代局部搜索算法对该问题进行求解。向婷等(2016)通过设置拆分阈值对客户进行聚类,然后采用蚁群算法优化各类的线路,即第一阶段将客户聚类成组,确定由同一辆车服务的客户集合;第二阶段将每一组客户和车场构成一个TSP回路,利用蚁群算法求解。Anthony等(2016)设计了多起点变邻域搜索算法求解最小拆分批量的SDVRP,通过两个程序生成初始解,引入4个算子进行邻域搜索。彭勇等(2017)以运输距离最短为目标建立模型,设计BLF-GA算法求解此问题,对交叉操作进行改进,并通过数值测试实验证明算法的有效性。揭婉晨等(2020)研究了带车辆数约束和最大行驶距离约束的SDVRP,以成本最小为目标建立模型,设计分支定价求解算法,通过对最大装载量和行驶成本等参数进行分析,验证了分支定价算法的应用价值。Pedro等(2020)研究了带有时间窗的需求可拆分车辆路径问题,建立基于路线的SDVRPTW模型,提出了一种基于列生成的启发式算法:在第一阶段,使用分支定价算法来求解VRPTW实例序列,生成一套可行路线;在第二阶段,用分支定界算法求解SDVRPTW实例应用于路由初始化的公式。徐翔斌等(2021)将车辆限行和二维装箱约束加入需求可拆分车辆路径问题,以车辆总配送成本最小为目标构建数学模型,设计了启发式算法来求解该模型,使用模拟退火算法确定需求拆分下的车辆配送路径,且在当前最优解判断时调用BLF算法检验物品的二维装箱约束。夏扬坤等(2021)研究了一种带客户分级和需求可拆分的生鲜车辆路径问题,构建了相应的多目标数学模型,并将自适应惩罚机制、多邻域结构体、禁忌表重新初始化等策略纳入禁忌搜索算法,设计了一种带动态禁忌表的自适应禁忌搜索算法进行求解。李华峰等(2021)以行驶距离和使用车辆之和最小为目标,提出一种改进的金字塔演化策略。王建伟等(2022)针对突发事件配送问题,将配送时间最短、加权时间攀比值最小和使用车辆数最少作为多维目标,构建了一种“效率—公平—运力”多维权衡的需求可拆分应急物资配送模型,并设计了一种改进的蚁群算法进行模型求解,通过选择拆分点、信息素更新和引入变邻域搜索算子三方面进行了算法改进。在精确求解算法方面,Archetti等(2014)提出了分支—切割算法,Gschwind等(2019)提出了分支定价切割算法。