




数学通常需要一点想象力,在初等几何中可以找到很多好的例子。
为了明白我的意思,请先拿一副圆规,用它来画一个圆,然后画出它的一条直径,端点为A和B(图18)。
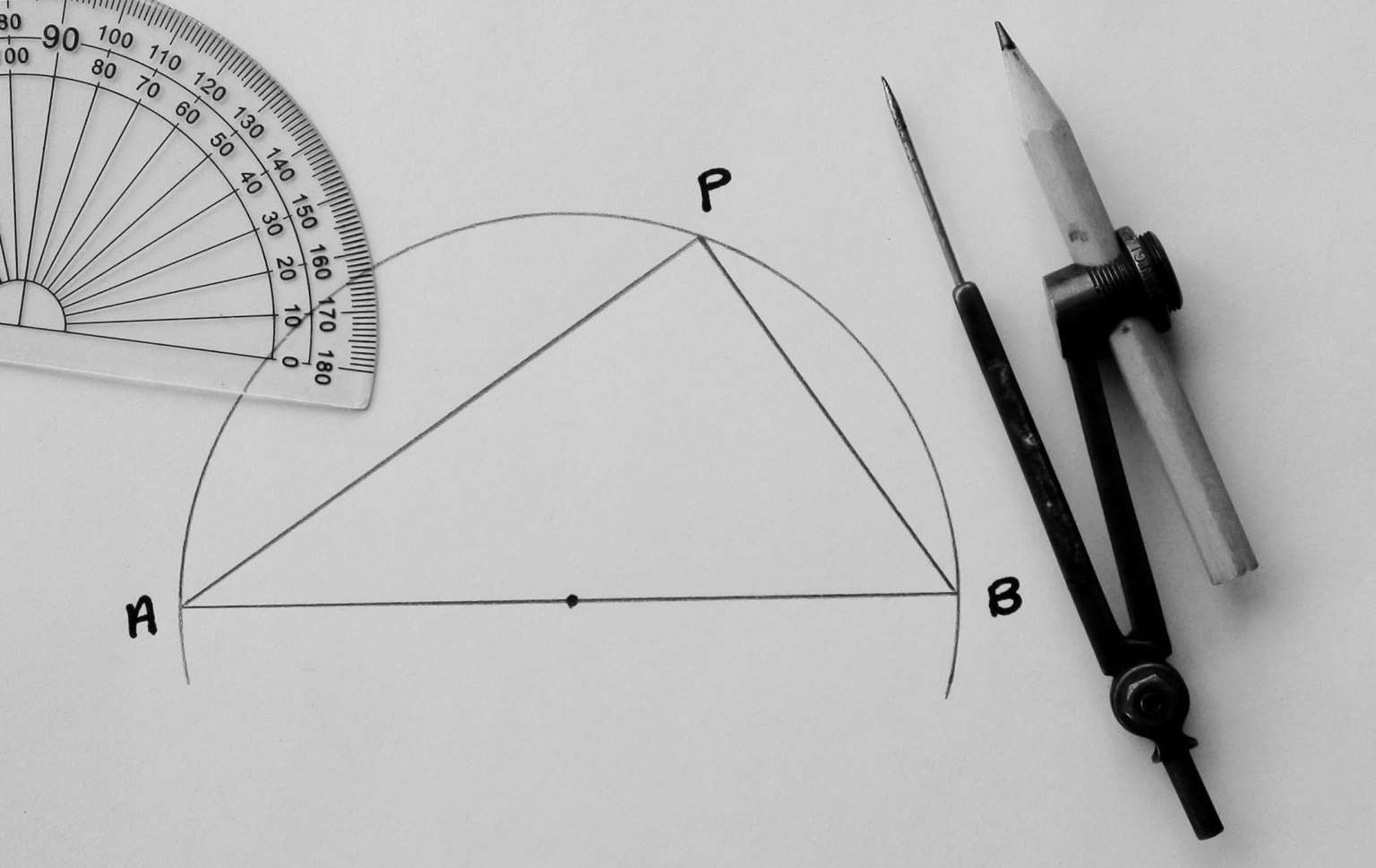
图18 泰勒斯定理
最后,取圆周上的任意点P,并用直线将其与A和B相连。
那么PA与PB的夹角总是90°。
这个令人惊讶的结果被称为泰勒斯定理(
Thales’s theorem
)
 ,可以追溯到公元前600年左右的古希腊。
,可以追溯到公元前600年左右的古希腊。
我们很快就会看到,要证明这一点是需要一点想象力的。
虽然人们有时认为是泰勒斯引入了几何学,将其作为一门严谨有序的、归纳演绎的学科,但真正将定理和证明的整个概念提升到新的、开创性高度的,是大约300年后的欧几里得(Euclid)。
尽管欧几里得的《几何原本》( Elements )有着极其简洁的阐述风格(甚至可能正因为如此),但它比人类历史上几乎任何其他书籍都有着更大的影响力,出版了更多的版本(图19)。

图19 欧几里得《几何原本》一个流行的英文版,译自德·沙勒(de Chasles)的法语原版
例如,在19世纪,伊顿公学有一位校长,人们曾经这样说他。
他把世界上的书分为三类:
第一类:《圣经》;
第二类:欧几里得的《几何原本》;
第三类:其他所有书。
为了证明泰勒斯定理,我们需要欧几里得早已证明了的两个关于三角形的结论。
第一个,如果我们有一个等腰三角形,即有两条边相等的三角形,那么它的两个“底角”总是相等的(图20)。

图20 一个等腰三角形
我猜测有很多人会觉得这个特殊的结论是相当显而易见的。毕竟,如果我们简单地“翻转”图20中的三角形,它看起来会和翻转前完全一样。
我们需要的第二个结论虽然是众所周知的,但我认为它远没有那么明显。这个结论是:任何三角形的三个内角相加之和都是180°。
在这方面,许多读者很可能会熟悉图21中的这个小实验。我们将一个纸三角形撕开,然后重新摆放这些碎片,将它们拼成看上去像一条直线,我认为值得说清楚这样做为什么不是一个证明。这不仅仅是因为这种方法有不可避免的“实验误差”,更根本的原因是,每次实验都仅涉及一个特定的三角形。

图21 三角形的内角和,取自W. D. 库利(W. D. Cooley)的《几何原理:简化与解释》( Elements of Geometry Simplifed and Explained ,1860)
然而,这个结论对任意三角形都是成立的。事实上,这正是我们未来的任务所需要的……
我们想证明,如果P是图18中半圆上的任意一点,那么∠APB=90°。
至少根据我的经验,我们几乎从来没有仅仅盯着原始图看,就能证明几何中的任何东西。我们几乎总是要对它做点什么。换句话说,我们必须摆弄这个问题,这样试试,再那样试试。
因此,想象一下,使点P离开该半圆,把它移到远离A和B的地方。至少对我来说,似乎很明显,这样我们就可以使∠APB变得很小。类似地,将P移动到离圆心O足够近的位置,我们就可以使∠APB尽可能接近180°。
这就表明,如果P的位置是任意的,那么我们要求的结论显然不成立,因此我们必须找到一种方法,从数学上来表达P位于半圆周上。
圆是用下面的性质来定义的:一个圆上的所有点到圆心O的距离都相同。所以最实际的方法似乎是连接线段OP,并注意到OP=OA=OB。
事实证明,这个稍微需要一点想象力的步骤是一个神来之笔,因为我们突然发现我们得到了两个等腰三角形。
因此,在图22中,两个“底角” a 相等,另外两个底角 b 也相等。

图22 泰勒斯定理的证明
最后,根据原始三角形APB的三个角加起来必定是180°,就有
a +( a + b )+ b =180°
所以,2( a + b )=180°,由此可得( a + b )=90°。所以∠APB=90°。这样,泰勒斯定理就得到了证明!