




数学最大的乐趣之一在于它所使用的一些实际方法,我一直很喜欢构成反证法基础的整个思想。
这种方法的主旨是要表明如果某个命题不成立,那就会出现某种矛盾或荒谬的情况,从而证明该命题成立。
这种证明方法的唯一缺点是,你通常无法事先知道矛盾或荒谬会如何产生。
因此,你必须保持头脑清醒!

图13 这是反证法?或者只是有点类似?夏洛克·福尔摩斯(Sherlock Holmes)的这句名言出现在《绿玉皇冠案》( The Adventure of the Beryl Coronet )中
为了说明反证法,我现在想借助于幻方这一实例,它是我所知道的用简单素材来呈现优雅数学的最佳例子之一。
幻方是指一个数字方阵,其中每一列、每一行、每条对角线上的数字之和都相同,这个和就称为这个幻方的“幻方常数” M 。
图14展示了一个最简单的例子,其中只用到前9个整数。
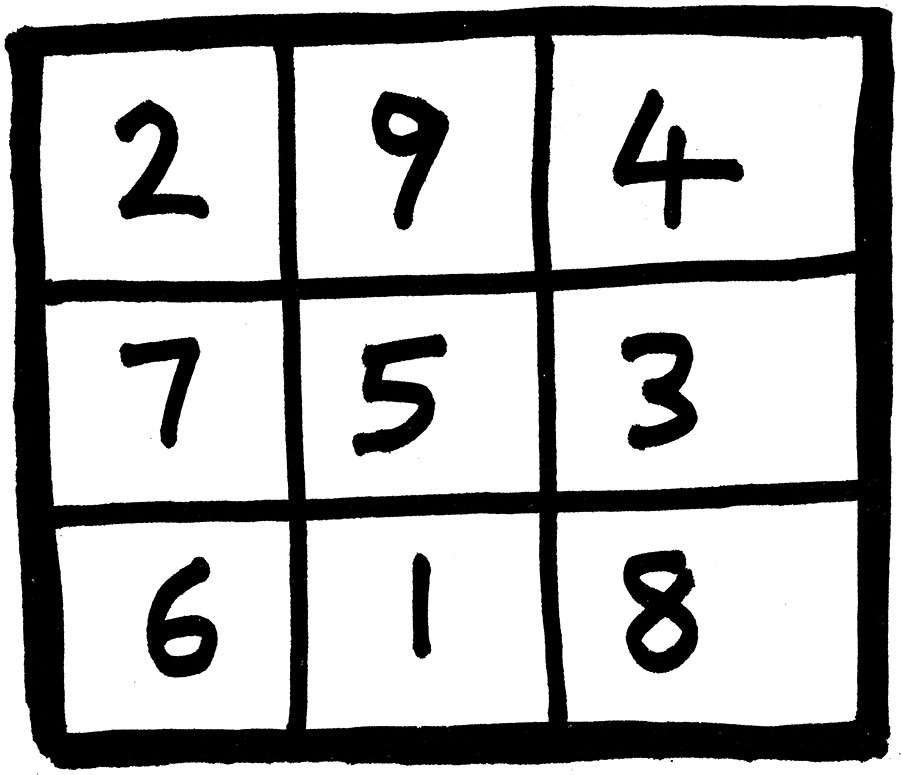
图14 一个幻方
但是,如何才能构造出这样一个幻方呢?
第一步是计算出幻方常数 M ,这很容易,因为1,…,9这些数加起来等于45,幻方中一共有3行,每一行之和就是 M 。
所以此时 M 一定是15。
答案是5,我们可以用反证法来证明。
首先假设图15中间格子里的数小于5,比如说是4。

图15 哪个数放中间?
于是接下来的问题是:1要放在哪里?我们无论把1放在哪里,都会发现有一些行、列或对角线上最多只能做到1+4+9=14,而不是15。如果中间格子里的数是3、2或1,同样的问题也会出现。
因此,中间格子里的数不能小于5。
如果我们把一个大于5的数放进中间格子,比如说6,我们就会遇到一个类似的问题:9要填在哪里才行?
所以中间格子的数字必须是5。
我们也可以用反证法来证明这一点。
那么,假设9可以填入一个角落的格子里(图16),在这种情况下,对角格子里的数必须是1。
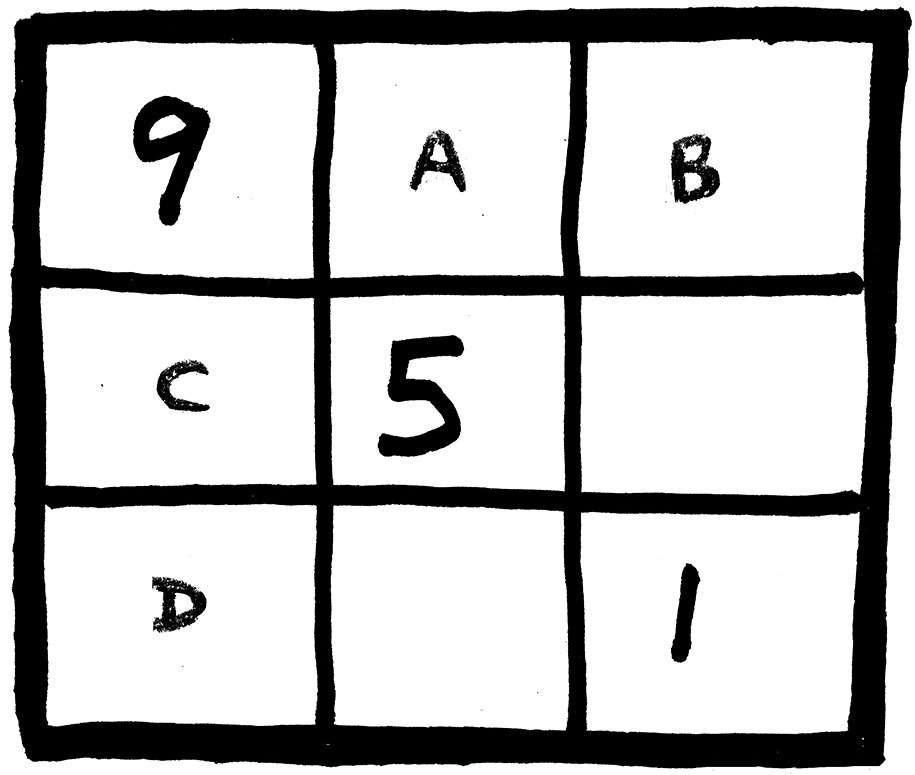
图16 采用反证法的另一个证明
但是这样一来,我们就需要图16中的A+B=6和C+D=6同时成立,然而这是不可能的,因为1和5已经“用掉”了,只剩下三个小于6的数字,即2、3和4。它们不可能同时满足上面这两个等式,所以9不能填入任意一个角落的格子里。
在将9填入一个非角落的格子后[图17(a)],我们现在需要E+F=6。现在只有2、3和4可以用,这样就有两种可能性:E=2,F=4或E=4,F=2。
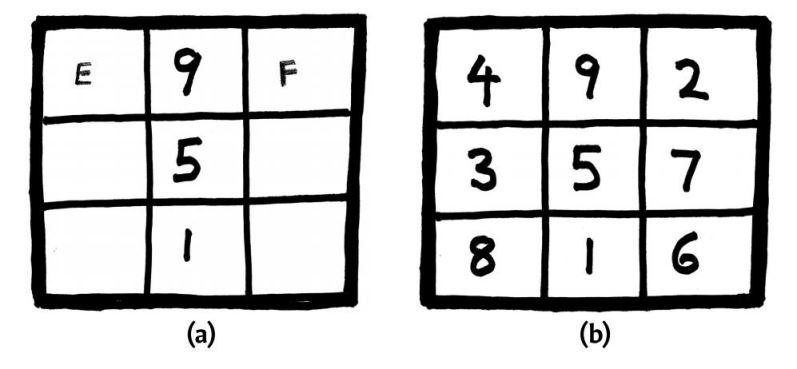
图17 最后几步
借助幻方常数15,若选择第一种可能性,我们再继续填下去,就会得出一开始的那个幻方(图14),若选择第二种可能性,就会得出图17(b),而这本质上是同一个幻方,只是从“背面”看而已。
事实上,仅包含1,2,…,9这九个数的幻方只有一个,其他的都是对图14的“微不足道”的重新排列,比如说旋转。
* * *
然而,尽管前面的一些论述确实阐明了反证法的概念,但是它们还没有真正反映出它的全部威力。
这是因为我们每次都只是用它摒弃了少量的其他可能性。
然而,可以说,只有当要被摒弃的其他可能性的数量无限多时,反证法的全部威力才会真正发挥出来。