




随机系统的分布形状控制是一个极具挑战性的问题,国际上一些学者针对随机系统的输出PDF形状控制问题也展开了一系列的研究。文献[9]~文献[13]采用静态优化和近似等方法实现随机系统输出PDF的闭环控制问题。然而,上述所提方法控制器输出为一个具有空间特征的PDF,众所周知,在每个采样时刻,控制器输出的是一个时域特征的数字值,而不是一个空间特性的分布函数,因此难以在实际工程中应用;同时,PDF具有正约束和积分约束等特点,上述方法往往忽略这些约束条件,难以获得合理的控制效果。与上述研究随机系统的输出PDF控制问题不同的是,如图1.2所示,本书所述的SDC方法主要研究如何采用单纯时间函数的PDF控制器 u ( k )实现动态随机分布系统的输出PDF形状控制。从理论上讲,设计一种特殊的控制器,不但能使系统输出PDF满足随机系统的控制性能,而且能降低外部随机干扰对控制系统的影响。因此,首先需要建立描述系统动态特性且便于分析的随机分布控制模型,利用建立的动态随机系统的模型,研究随机分布系统在不同性能指标下易于工程实现的控制策略。
在实际工业过程中,关于一些变量的分布形状控制问题一直是一个极具挑战性的难题,如在造纸过程中,决定纸张质量的关键是絮凝粒径分布形状 [14-17] ;在聚合反应中,分子链长度分布形状是衡量化工生产过程产品质量的重要标志 [18-20] 。这些变量最终可以看作关于输出随机变量的PDF形状控制问题,然而,这些输出变量的PDF,既是空间变量的函数,也是时间变量的函数,且具有积分约束及较强的随机性和非线性,因此,非高斯工业过程输出PDF建模与控制问题一直是控制理论与应用研究的难点。
为了进一步描述动态非高斯随机分布系统的模型,本节简要描述随机变量的定义和随机分布系统模型表示方法。假设 y ∈[ a , ξ ], a , ξ ∈R为描述动态随机系统输出的一致有界随机变量, u ( k )∈R m 为 k 时刻控制随机系统输出分布形状的 m 维控制输入,在任意采样时刻 k ,随机变量 y 就可以通过其概率密度函数(Probability Density Function,PDF)来描述,其定义式如下:
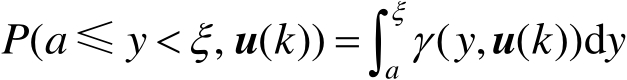
(1.1)
式中, P ( a ≤ y < ξ , u ( k ))为随机系统在 k 时刻控制输入 u ( k )作用下输出随机变量 y 落在区间[ a , ξ ]内的概率; γ ( y , u ( k ))为输出随机变量 y 的PDF,即 γ ( y , u ( k ))形状由控制输入 u ( k )控制。
事实上,随机系统输出PDF形状可以通过固定结构的神经网络[如B样条神经网络 [21-25] 、径向基函数(Radial Basis Function,RBF)神经网络 [26-29] 等]来逼近,这类神经网络由基函数及其相对应的权值组成,这样就可以将神经网络的权值与随机分布系统的控制输入 u ( k )联系起来。下面以B样条神经网络模型为例,说明动态随机分布系统模型的表示方法。首先,对于任何一个确定的控制输入 u ( k ), γ ( y , u ( k ))对所有 y ∈[ a , ξ ]连续。存在一个B样条神经网络需满足如下不等式:
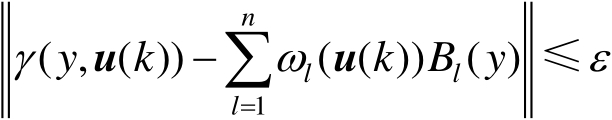
(1.2)
式中, ε 为一个预先指定的任意小的正数; B l ( y )( l =1,2,⋯, n )为预先定义在区间[ a , ξ ]的确定的B样条基函数; ω l ( u ( k ))为B样条基函数相对应的权值。从式(1.2)可以看出,所有基函数一旦确定,则权值 ω l ( u ( k ))可以看作控制输入 u ( k )的函数,即不同时刻的控制输入 u ( k )产生不同的权值 ω l ( u ( k )),故式(1.2)可以进一步表示为
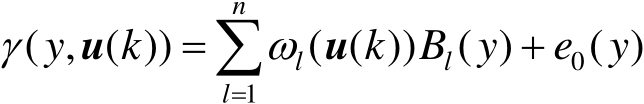
(1.3)
式中, e 0 ( y )为近似误差。B样条神经网络逼近原理如图1.3所示,可以看出,通过B样条基函数建立了控制输入 u ( k )与输出 γ ( y , u ( k ))之间的关系。当所有基函数 B l ( y )确定后,输出PDF形状的控制可以通过控制神经网络的权值 ω l ( u ( k ))来实现。
同时,考虑到PDF满足在其定义的区间积分为1的自然约束,即
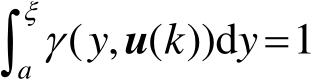
(1.4)
从式(1.4)所示的约束条件可以看出,在 n 个权值中只有 n −1个权值是相互独立的,且权向量为约束变量。此时,式(1.3)可以表示如下:
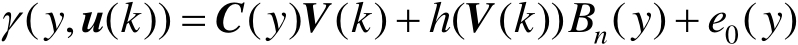
(1.5)
式中, C ( y )=[ B 1 ( y ), B 2 ( y ),⋯, B n −1 ( y )]; V ( k )=[ ω 1 ( u ( k )), ω 2 ( u ( k )),⋯, ω n −1 ( u ( k ))] T 为由前 n −1个权值组成的向量形式; h ( V ( k ))为前 n −1个权值的函数表达式。可以看出,权值向量的动态主要取决于控制输入 u ( k ),因此,前 n −1个权值组成的向量 V ( k )和控制输入 u ( k )之间的动态关系可以表示为
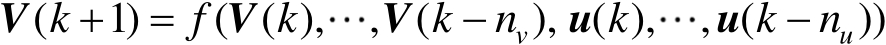
(1.6)
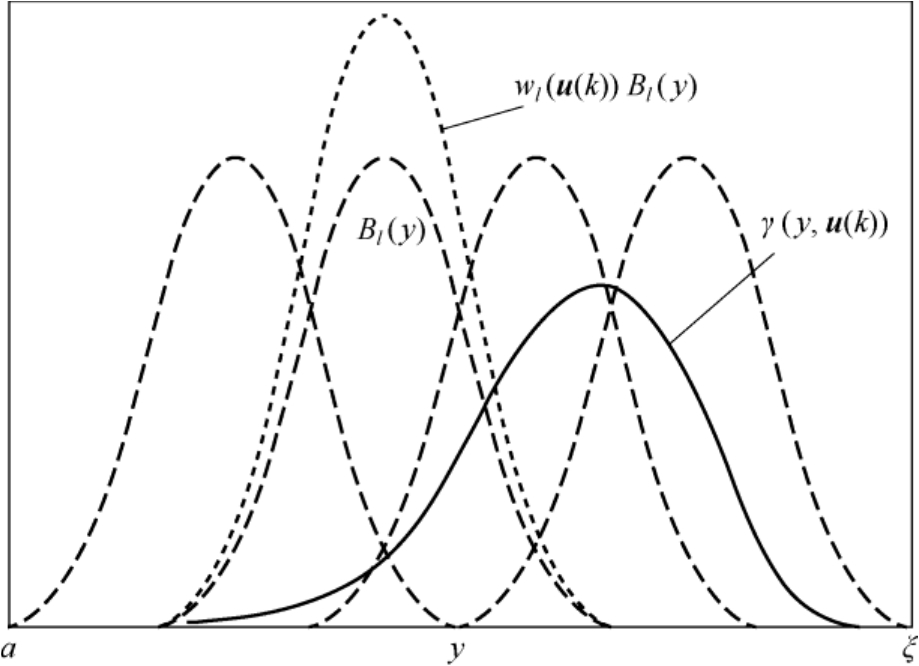
图1.3 B样条神经网络逼近原理
式中, f (·)为表征控制输入 u ( k )和权值向量 V ( k )之间关系的函数,其可以采用常规的线性函数表示,如状态空间方程、差分方程、微分方程等,也可以采用任意非线性函数表示,如神经网络模型、最小二乘支持向量机模型等; n v 和 n u 分别为权值输出和控制输入的最大时滞常数。因此,动态随机分布系统的控制输入 u ( k )和输出PDF之间的动态关系可以通过如式(1.3)和式(1.5)所示的系统来描述。
根据B样条神经网络对输出PDF逼近方法的不同,将动态随机分布系统分为线性B样条模型 [21-23,30] 、均方根B样条模型 [24,30-35] 、有理B样条模型 [36,37] 、有理平方根B样条模型 [6,38] 四种,它们之间相互联系,均能描述随机分布系统的动态特性,相互转化形成一个相互统一的整体。但是,这些模型具有不同的性质,主要表现在不同模型的B样条基函数相对应的权值向量的约束不同,四种B样条模型性质详细分析见文献[36]。此外,RBF神经网络和B样条神经网络同样对任意的非线性函数具有较高的逼近精度,不同的是,RBF神经网络的激活函数采用高斯基函数,相对于B样条基函数,高斯基函数具有参数(中心值和宽度)少、形状易于调节、实现简单等优点。因此,与B样条神经网络对输出PDF逼近方法类似,采用RBF神经网络同样可以得到类似的动态随机分布模型 [26-29] 。
可以看出,式(1.3)和式(1.6)所示的随机系统模型与传统的随机微分方程有明显的不同,采用随机微分方程描述的系统均假设其输出符合高斯分布,而式(1.3)和式(1.6)所示的随机分布系统的输出可以为非高斯分布类型,利用实际测量的输出PDF作为反馈信息,所设计的控制器是一个典型的反馈控制器,其主要目的是使系统的输出PDF形状跟踪一个期望的PDF形状。因此,SDC问题可以看作如何将一个无限维随机控制问题转化为一个有限维的控制问题,这种处理方法将会大大降低控制器设计难度。另外,随机分布系统动态主要取决于式(1.6)所示的时域内权值向量的动态,而式(1.6)所示权值向量的动态可以采用常规的线性状态空间方程和微分方程等表示,也可以采用非线性回归模型。因此,当输出变量和权值向量数据可知时,通常采用子空间辨识或者最小二乘估计方法建立权值向量的线性动态模型 [26-29] ,也可以利用如神经网络、最小二乘支持向量机等智能建模方法建立权值向量的非线性动态关系 [39,40] 。
通常情况下,随机分布控制系统输出PDF通常采用神经网络等(如B样条神经网络、RBF神经网络)逼近,并利用式(1.3)所示输出PDF的基函数近似部分和式(1.6)所示神经网络权值向量的动态部分组成的随机分布系统模型,提出一系列随机分布系统输出PDF控制方法。例如,基于梯度优化输出PDF控制 [23-25] 、固定控制结构PDF控制 [41-43] 、迭代学习输出PDF控制 [26-28] 、预测PDF控制 [6,7,18,20,44] 、自适应PDF控制 [45-47] 和滑模PDF控制 [48] 等。
(1)基于梯度优化输出PDF控制:针对具有式(1.6)所示的随机分布系统动态,通过极小化控制系统的性能指标,采用梯度优化方法设计PDF控制器。例如,文献[23]针对多输入多输出随机系统,当系统收到有界未知输入时,通过极小化二次型性能指标获得PDF控制器的鲁棒解析解,保证闭环系统的稳定性。文献[24]考虑到系统由于收到有界随机输入导致模型误差或者不确定性,通过建立广义非线性随机系统的输入噪声分布与输出分布之间的关系设计控制器,使系统输出PDF形状尽可能接近给定形状,并给出一种闭环系统鲁棒性分析方法。另外,文献[23]和文献[24]均假设给定一个期望PDF,然而,当期望的PDF无法获得时,通过优化系统输出变量的香农熵来完成PDF控制器的设计,降低了随机系统的随机性和不确定度 [ 25] 。事实上,最小熵控制可以看作传统最小方差控制的推广。然而,随机系统的最小熵控制只能反映系统输出变量的不确定度,当考虑对期望PDF的跟踪控制时,常通过优化引入输出变量均值项的性能指标,实现控制器的设计 [30,31] 。
(2)固定控制结构输出PDF控制:采用优化性能指标方法设计的PDF控制器虽然能够保证闭环系统的稳定性,但是闭环系统没有明显的反馈结构,给控制器的工程实现和闭环系统的收敛性、稳定性和鲁棒性分析带来了困难。为了便于PDF控制器工程实现及闭环系统的控制性能分析,通常将PDF控制器设计为工业中广泛应用的PID控制器结构,这里所述的PID控制器并非传统的PID控制器,而是以实现闭环输出PDF跟踪为目的的积分型广义PID控制器 [ 41-43] 。例如,文献[41]利用线性B样条PDF模型和广义PID控制器构造权值向量的闭环系统,并且考虑到当模型存在有界不确定性和外部干扰时,利用求解线性矩阵不等式(Linear Matrix Inequality,LMI)实现PID参数的鲁棒性设计,使输出PDF在一定误差范围内跟踪期望的输出PDF,保证了闭环系统的稳定性。文献[42]提出了基于两步神经网络输出PDF的广义PI控制方法。文献[43]利用均方根B样条PDF模型和广义PI控制器构造的权值闭环系统,将输出PDF跟踪控制转化为具有约束的权值控制,采用线性矩阵不等式技术设计,实现输出PDF跟踪的广义PI控制器,保证闭环系统的稳定性、状态约束和跟踪性能。
(3)迭代学习输出PDF控制:对式(1.3)和式(1.6)所示的动态随机分布系统输出PDF建模时,通常情况下,B样条基函数参数是固定的,这就意味着该参数只考虑随机分布系统的时域动态特性,而忽略了其空间变化的动态特性。然而,对于具有复杂动态特征的随机分布系统,需要较多数量的B样条基函数才能逼近输出PDF,这使动态模型的维数过高,同时需要选择合适的阶次和节点,导致建模时间过长、模型精度不高。另外,高维模型也增加了PDF控制器的设计难度,因此,当采用固定基函数建模时,通常很难获得描述复杂的随机分布系统动态。为了提高动态随机分布系统模型的精度,同时降低PDF控制器的设计难度,文献[26]~文献[29]采用RBF神经网络逼近的PDF模型,通过引入迭代学习控制(Iterative Learning Control,ILC) [49-53] 思想,将输出PDF控制时间区间分为若干个固定长度的周期,每个周期内的RBF基函数均是固定的,并且在每个周期内基于重新构建的PDF模型完成闭环控制。根据ILC可以利用当前闭环周期运行效果来校正下一个闭环周期运行效果的特点,在周期与周期之间对RBF基函数和权值不断迭代更新,将更新的RBF基函数和动态PDF模型产生新的控制作用于下一个周期的操作。因此,将迭代学习控制原理引入SDC中,不仅可以改善时域变量的控制效果,而且能保证输出PDF空间变量的动态调节。
此外,在随机分布系统输出PDF建模和控制研究的基础上,进一步提出了随机分布系统的滤波和估计 [54,55] ,以及随机分布系统的故障诊断与容错控制 [56-59] 、鲁棒PDF控制 [23,33,60] 、预测PDF控制 [5-7,18,20,44] 、智能PDF控制 [ 29] 、自适应PDF控制 [45,46] 、变结构PDF控制 [ 49] 等,以上研究成果进一步完善和深化了SDC理论体系,也为一些实际工业过程中的分布控制问题的应用研究提供了较丰富的理论指导。