




B样条神经网络作为一种基于样条函数插值原理而设计的神经网络,其输入空间定义在 n 维网格上,网格结构的每个元胞均定义了基函数。基函数可以通过局部学习和训练来改变其对应的位置,即改变其中一部分输入空间几乎不改变其他的输入响应。输入轴被分为许多区间,其节点为地址位置。因此,每个输入轴的节点向量包含整个区间被节点分成的子区间值,而这些节点可以根据实际需要设计。
B样条神经网络建模的性能同其基函数的阶次密切相关,阶次不仅决定了B样条的阶次可微性,而且决定了B样条函数的宽度和区间。例如,一个阶次为 k 且可微的B样条基函数宽度可分为 k 个子区间,每个输入子区间都被映射到 k 个非零B样条基函数。随着阶次的增加,函数越来越光滑。因此,B样条基函数可按照如下的递推式得到:
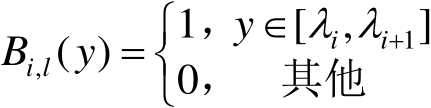
(2.1)
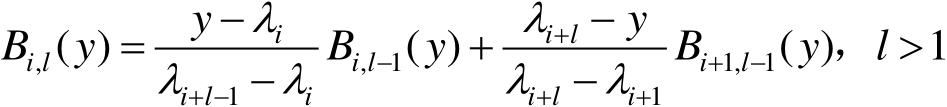
(2.2)
显然,对于任意 l ≥1,B样条基函数满足
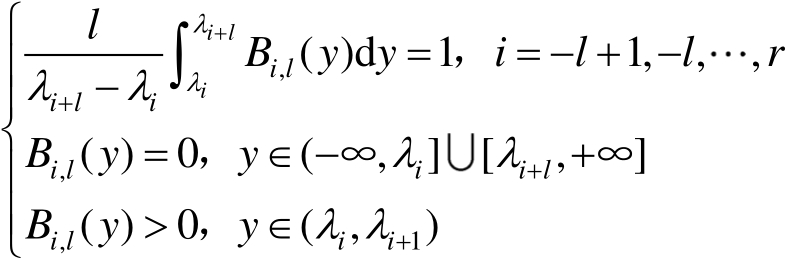
(2.3)
式(2.3)描述了B样条基函数在有效区间的性质及对应的有效区间的宽度。当 l ≥3时,基函数在区间(− ∞ , ∞ )内为一个光滑的函数。在大多数情况下,一般采用三阶B样条神经网络,三阶B样条基函数可以描述为
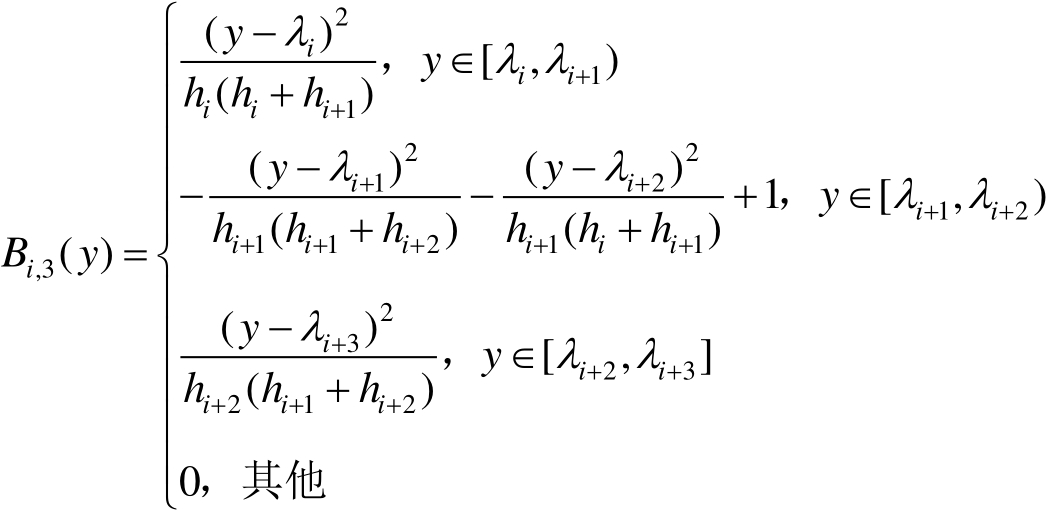
(2.4)
式中, h j = λ j − λ j −1 ( j = i , i +1, i +2)。任意定义的连续函数都可以用B样条神经网络来逼近,因此,本书讨论的随机系统也可以用B样条神经网络来解耦控制输入变量和输出PDF之间的关系。根据B样条基函数的逼近方式的不同,已经形成了不同的B样条模型。下面将基于B样条模型建模机理来说明随机分布系统的建模机理。
记 v ( t )∈R 1 为一个定义在 T =[0,+ ∞ )上的一致有界的随机变量,即
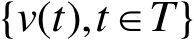
(2.5)
并假定 v ( t )表示随机分布系统的输出。假设 u ( t )∈R m 为控制随机变量 v ( t )的分布形状的输入向量,则考虑随机系统可以表示为
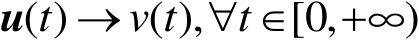
(2.6)
在任意时刻,随机变量 v ( t )分布可以用它的累计概率分布函数 F ( y , u ( t ))来表述:
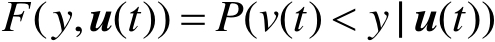
(2.7)
式中, P ( v ( t )< y | u ( t ))表示在控制输入 u ( t )作用下随机变量 v ( t )小于 y 的概率。假定累计概率分布函数 F ( y , u ( t ))是关于 y 的连续函数,则由概率论的相关知识可得到对应的PDF,记为 γ ( y , u ( t )),即
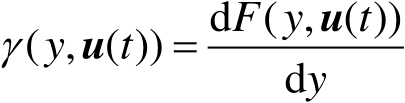
(2.8)
故可以得出随机变量PDF形状由控制输入 u ( t )决定。此时,假定随机变量的PDF为关于控制输入 u ( t )和 y 的连续函数,且随机变量 v ( t )一致有界,故存在一个已知的区间[ a , b ],使得
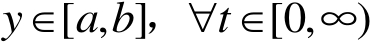
(2.9)
成立。对于任意给定的控制输入 u ( t )及所有的 y ∈[ a , b ], γ ( y , u ( t ))为 y 的连续函数,由B样条神经网络的理论可知 [ 3] ,存在一个神经网络使得如下不等式成立:
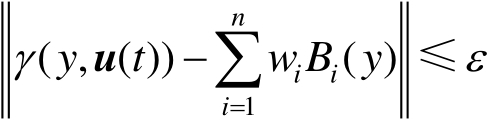
(2.10)
式中, ε 为一个任意小的正常数; B i ( y )( i =1,2,⋯, n )为先前在区间[ a , b ]上确定的B样条基函数; w i 为基函数相对应的权值。可以看出,当所有的基函数固定时,不同的控制输入 u ( t )可以产生不同的权值向量,这表明权值 w i 是控制输入 u ( t )的函数。因此,式(2.10)可以进一步表示为
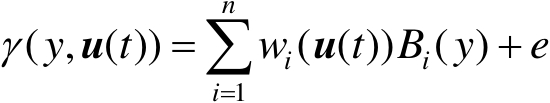
(2.11)
式中, e 为输出随机变量PDF的逼近误差,且‖ e ‖≤ δ 。由此可见,通过基函数建立了控制输入 u ( t )和输出PDF之间的关系,输出PDF形状的变化可以被认为是由其对应的权值 w i 变化引起的,因此,进一步综合控制输入 u ( t )和权值 w i 之间的动态模型,便可获得描述随机分布系统动态的输出PDF模型。