




(1)阶乘:n!=1·2·3…( n -2)( n -1) n
0!=10!!=0(-1)!!=0
MATLAB(关于MATLAB基础知识,请参见第12篇第8章中阶乘函数 [30-34] :factorial
格式: y =factorial(n)
描述:factorial(n)表示从1到n所有整数的乘积。由于其结果为双精度,只有大概15位数字,所以其只能精确求解n≤21,对于更大的n值,其结果将适当扩大,而且前15位是精确的。
(2)排列:
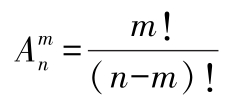
(3)组合
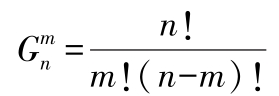
(4)二项式定理:
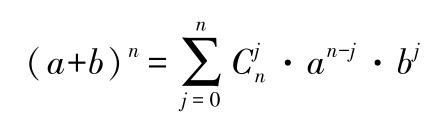
若:
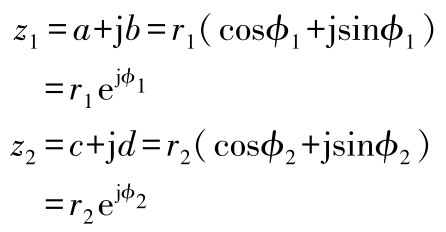
则:
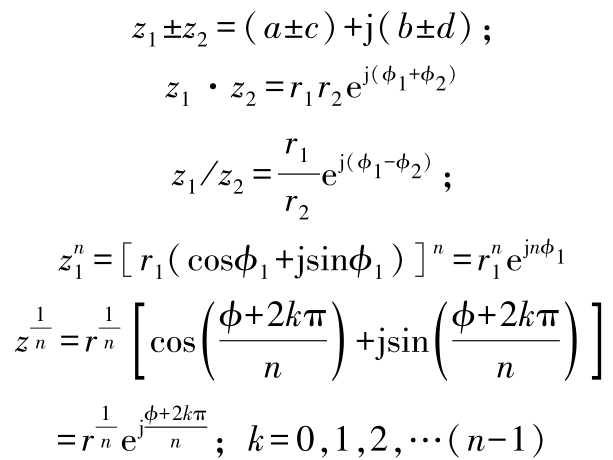
z
=
a
+j
b
的共轭复数:
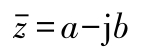
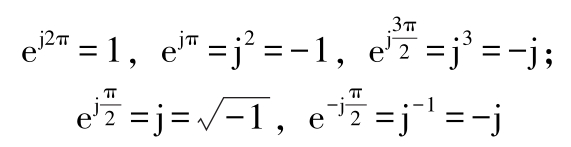
♣MATLAB中复数的定义函数:complex
格式:c=complex(a,b)
c=complex(a)
描述:1)c=complex(a,b)输入两个实数,构成一个复数输出c=a+bi,输入必须是标量或尺寸相同、数据类型相同的向量、矩阵、多维数组,输出和输入的尺寸一样。注意:如果b是全零,c仍是复数,且它的所有虚部为零。相反,加法a+0i返回的是一个实数结果。2)c=complex(a)返回结果为一复数形式,其实部为a,虚部为0,即使所有虚部均为0,c仍是复数,复数的表达形式为a+i*b或a+j*b,当a和b不是双精度或b为全零时,“i”和“j”可当作其他变量(不等于
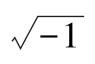 )。
)。
(1)基本恒等式
sin α csc α =1 cos α sec α =1
tan α cot α =1 sin 2 α +cos 2 α =1
csc 2 α -cot 2 α =1 sec 2 α -tan 2 α =1
tan α =sin α /cos α cot α =cos α /sin α
(2)和(差)角公式
sin( α + β )=sin α cos β +cos α sin β
sin( α-β )=sin α cos β -cos α sin β
cos( α + β )=cos α cos β -sin α sin β
cos( α-β )=cos α cos β +sin α sin β
tan( α ± β )=(tan α ±tan β )/(1∓tan α tan β )
cot( α ± β )=(cot α cot β ±1)/(cot β ±cot α )
(3)倍角公式
sin2 α =2sin α cos α
cos2 α =cos 2 α -sin 2 α =1-2sin 2 α =2cos 2 α -1
tan2 α =2tan α /(1-tan 2 α )
cot2 α =(cot 2 α -1)/(2cot α )
sin3 α =3sin α -4sin 3 α
cos3 α =4cos 3 α -3cos α
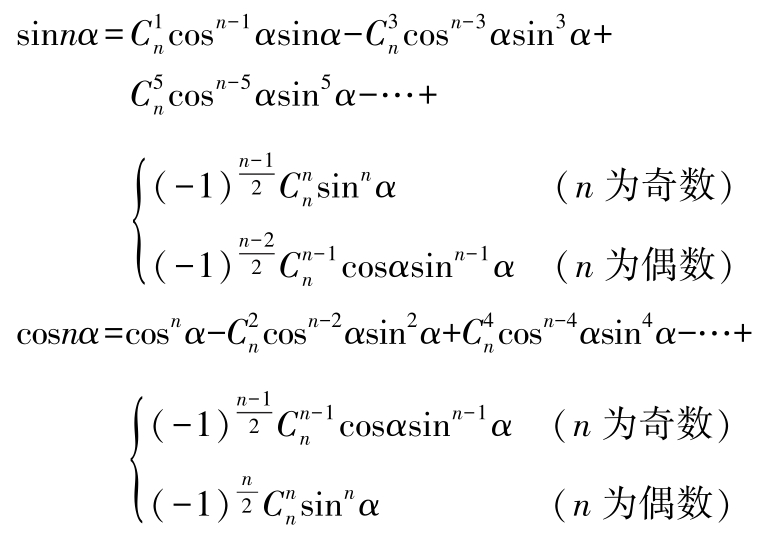
(4)半角公式
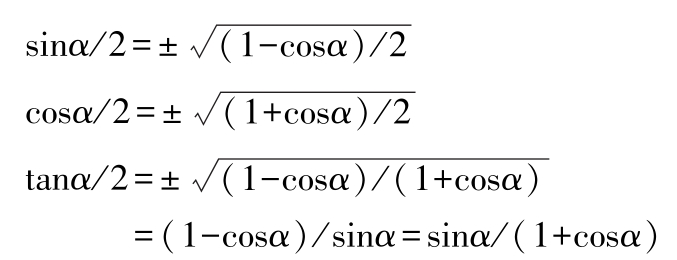
(5)和差与积互化公式
sin α +sin β =2sin[( α + β ) / 2]cos[( α-β ) / 2]
sin α -sin β =2cos[( α + β ) / 2]sin[( α-β ) / 2]
cos α +cos β =2cos[( α + β ) / 2]cos[( α-β ) / 2]
cos α -cos β =-2sin[( α + β ) / 2]sin[( α-β ) / 2]
tan α +tan β =sin( α + β ) / cos α cos β
tan α -tan β =sin( α-β ) / cos α cos β
2cos α cos β =cos( α + β )+cos( α-β )
(6)反三角函数
sin(arcsin x )=cos(arccos x )=tan(arctan x )= x
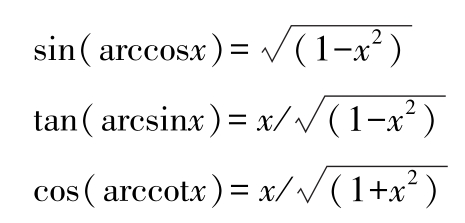
arcsin x +arccos x =π/2
arctan x +arccot x =π/2
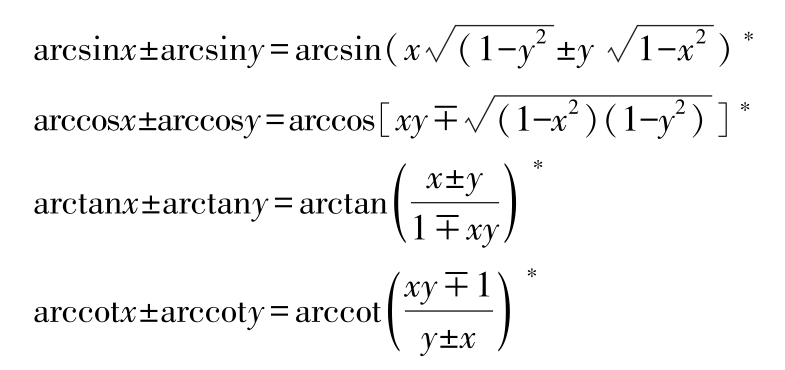
(*上面四等式左边两角之和与差在主值范围内取值时,等式成立)
♣MATLAB中正弦函数与反正弦函数:sin、asin
格式:Y=sin(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的正弦值Y,所有分量的角度单位为rad。
格式:Y=asin(X)计算参量X(可以是向量、矩阵)中每个元素的反正弦函数值Y。若X中有的分量处于[-1,1]之间,则Y=asin(X)对应的分量处于[-π/2,π/2]之间,若X中有分量在[-1,1]之外,则Y=asin(X)对应的分量为复数。
注意:sin(pi)并不是零,而是与浮点精度有关的无穷小量eps,因为pi仅仅是精确值π浮点近似的表示值而已;对于复数z=x+iy,函数的定义为:
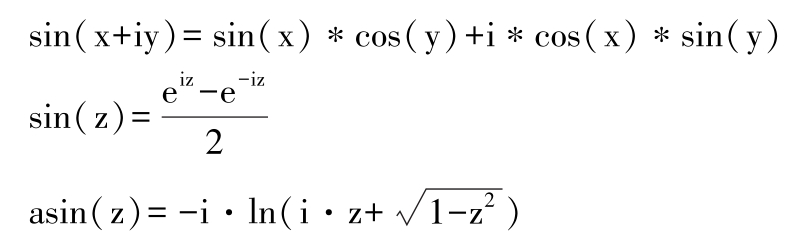
♣MATLAB中余弦函数与反余弦函数:cos、acos
格式:Y=cos(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的余弦值Y,所有分量的角度单位为rad。
格式:Y=acos(X)计算参量X(可以是向量、矩阵)中每个元素的反余弦函数值Y。若X中有的分量处于[-1,1]之间,则Y=acos(X)对应的分量处于[0,π]之间,若X中有分量在[-1,1]之外,则Y=acos(X)对应的分量为复数。
注意:cos(pi/2)并不是零,而是与浮点精度有关的无穷小量eps,因为pi仅仅是精确值π浮点近似的表示值而已;对于复数z=x+iy,函数的定义为:
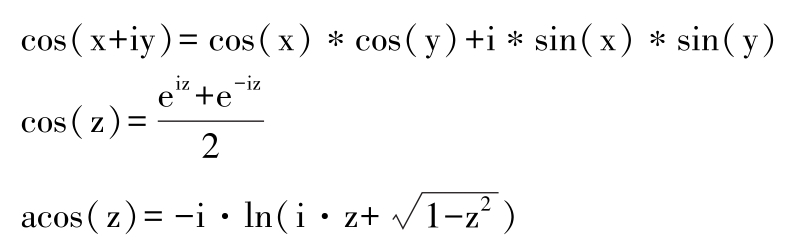
♣MATLAB中正切函数与反正切函数:tan、atan
格式:Y=tan(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的正切值Y,所有分量的角度单位为rad。
格式:Y=atan(X)计算参量X(可以是向量、矩阵)中每个元素的反正切函数值Y。若X中有的分量为实数,则Y=atan(X)对应的分量处于[-π/2,π/2]之间。
注意:tan(pi/2)并不是零,而是与浮点精度有关的无穷小量eps,因为pi仅仅是精确值π浮点近似的表示值而已;反正切函数的定义为:
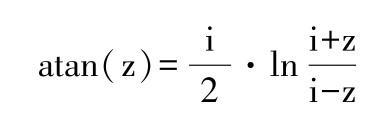
♣MATLAB中余切函数与反余切函数:cot、acot
格式:Y=cot(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的余切值Y,所有分量的角度单位为rad。
格式:Y=acot(X)计算参量X(可以是向量、矩阵)中每个元素的反余切函数值Y。
♣MATLAB中正割函数与反正割函数:sec、asec
格式:Y=sec(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的正割函数值Y,所有分量的角度单位为rad。
格式:Y=asec(X)计算参量X(可以是向量、矩阵)中每个元素的反正割函数值Y。
注意:sec(pi/2)并不是无穷大,而是与浮点精度有关的无穷小量eps的倒数,因为pi仅仅是精确值π浮点近似的表示值而已。
♣MATLAB中余割函数与反余割函数:csc、acsc
格式:Y=csc(X)计算参量X(可以是向量、矩阵,元素可以是复数)中每个角度分量的余割值Y,所有分量的角度单位为rad。
格式:Y=acsc(X)计算参量X(可以是向量、矩阵)中每个元素的反余割函数值Y。
(1)双曲函数
双曲正弦
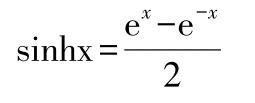
双曲余弦
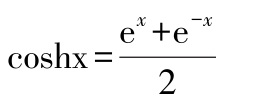
双曲正切
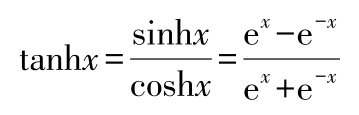
双曲余切
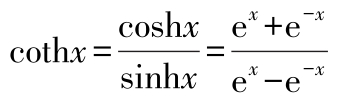
双曲正割
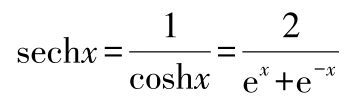
双曲余割
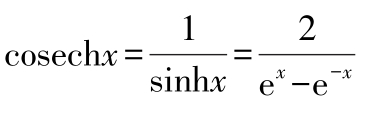
(2)双曲函数的基本关系
sinh( -x )=-sinh x
cosh( -x )=cosh x
tanh x coth x =1
cosh 2 x -sinh 2 x =1
sech 2 x +tanh 2 x =1
coth 2 x -cosech 2 x =1
反双曲正弦 若 x =sinh y ,则:
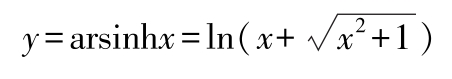
反双曲余弦 若 x =coshy,则:
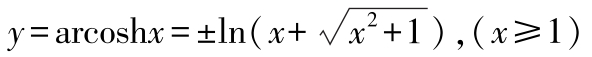
反双曲正切 若 x =tanh y 则:
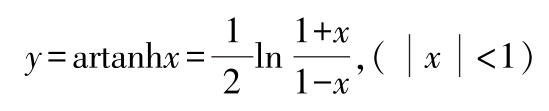
反双曲余切 若 x =coth y ,则:
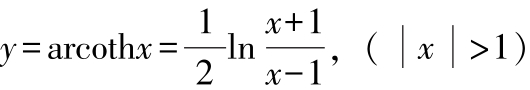
反双曲正割 若 x =sech y ,则:
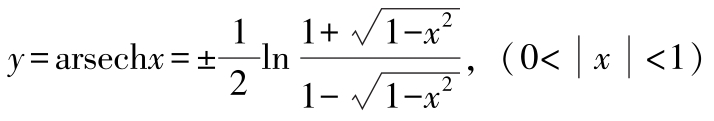
反双曲余割 若 x =cosech y ,则:
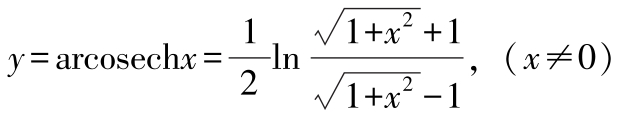
反双曲函数基本公式
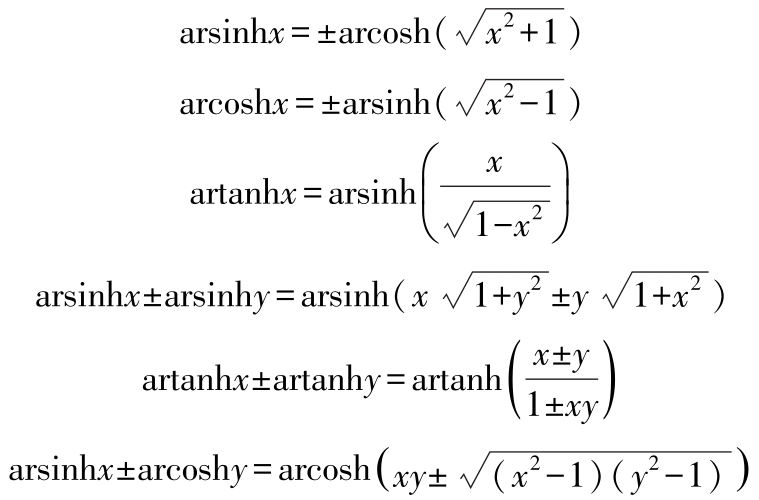
(3)对数函数
log a a =1; log a 1=0
log a x n = n log a x ; a log a x = x
log a ( x · y )=log a x +log a y
log a ( x/y )=log a x -log a y
log a x =log b x/ log b a ; log a b ·log b a =1
♣MATLAB中双曲正弦函数与反双曲正弦函数:sinh、asinh
格式:Y=sinh(X)计算参量X的双曲正弦函数值Y。
Y=asinh(X)计算参量X中每一个元素的反双曲正弦函数值Y。
♣MATLAB中双曲余弦函数与反双曲余弦函数:cosh、acosh
格式:Y=cosh(X)计算参量X的双曲余弦值Y。
Y=acosh(X)计算参量X中每一个元素的反双曲余弦函数值Y。
♣MATLAB中双曲正切函数与反双曲正切函数:tanh、atanh
格式:Y=tanh(X)计算参量X中每一个元素的双曲正切函数值Y。
Y=atanh(X)计算参量X中每一个元素的反双曲正切函数值Y。
♣MATLAB中双曲余切函数与反双曲余切函数:coth、acoth
格式:Y=coth(X)计算参量X中每一个元素的双曲余切函数值Y。
Y=acoth(X)计算参量X中每一个元素的反双曲余切函数值Y。
♣MATLAB中双曲正割函数与反双曲正割函数:sech、asech
格式:Y=sech(X)计算参量X中每一个元素的双曲正割函数值Y。
Y=asech(X)计算参量X中每一个元素的反双曲正割函数值Y。
♣MATLAB中双曲余割函数与反双曲余割函数:csch、acsch
格式:Y=csch(X)计算参量X中每一个元素的双曲余割值Y。
Y=acsch(X)计算参量X中每一个元素的反双曲余割函数值Y。
♣MATLAB中对数函数:log、log 10 、log 2
格式:Y=log(X)自然对数函数。
Y=log 10 (X)常用对数函数。
Y=log 2 (X)以2为底的对数并分解浮点数。
e j x =cos x +jsin x ; e x =cosh x +sinh x ;
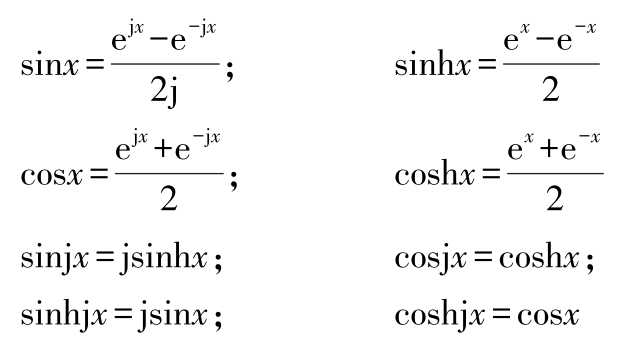
(1)导数运算基本规则 若 c 为常数,函数 u = u ( x ), v = v ( x )的导数存在,则
( c ) ′ =0( c′ 为 c 的导数)( cu ) ′ = cu′
( u ± v ) ′ = u′ ± v′ ( uv ) ′ = u′v + uv′
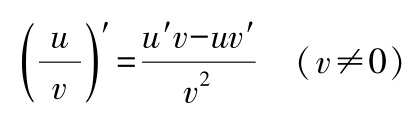
设 y = f ( u ), u = g ( x ),则
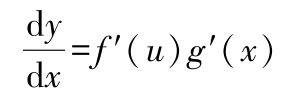
设 y = g ( t ), x = f ( t ),则
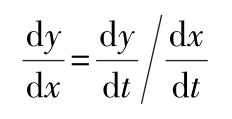
(2)基本函数的导数公式见表1.4-1。
表1.4-1 基本函数的导数公式

(续)

♣MATLAB中一元函数的导数函数:diff
格式:yy=diff(f)求函数f的一阶导数,其中f是符号函数。
yy=diff(f,n)求函数f的n阶导数,其中f是符号函数。
(1)不定积分 不定积分的基本性质:
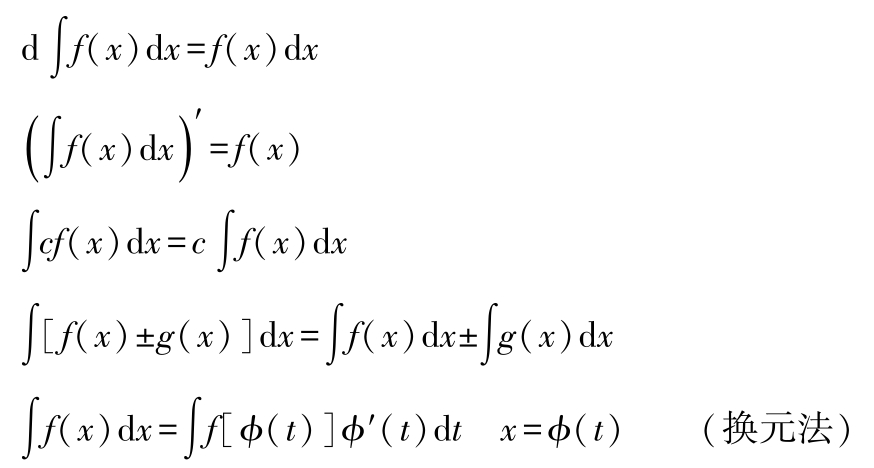
基本函数积分表:
∫ k d x = kx + c ( k 为常数)
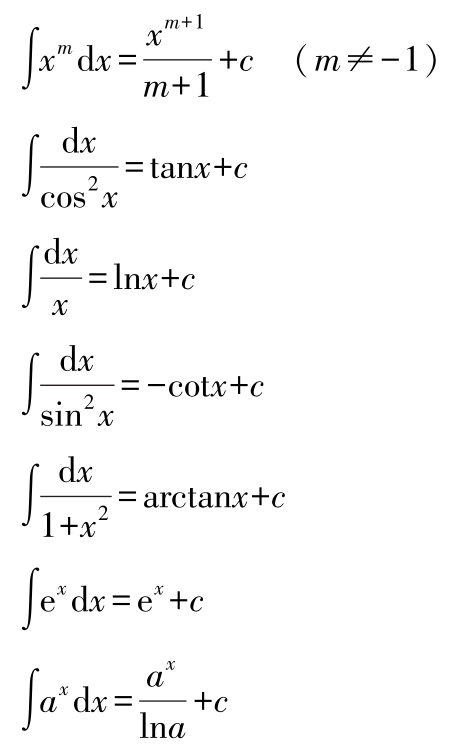
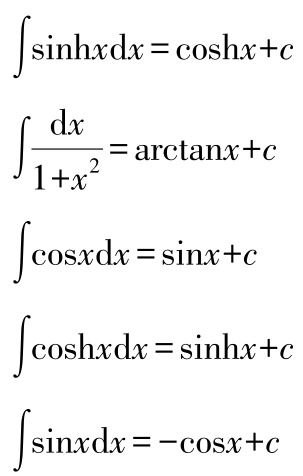
(2)部分常用函数定积分
1)伽马( Γ )函数:
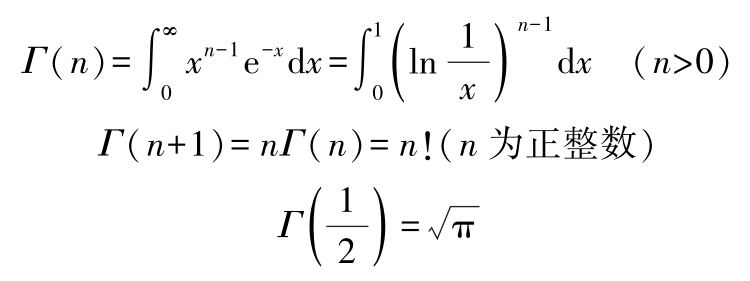
2)尤拉常数:
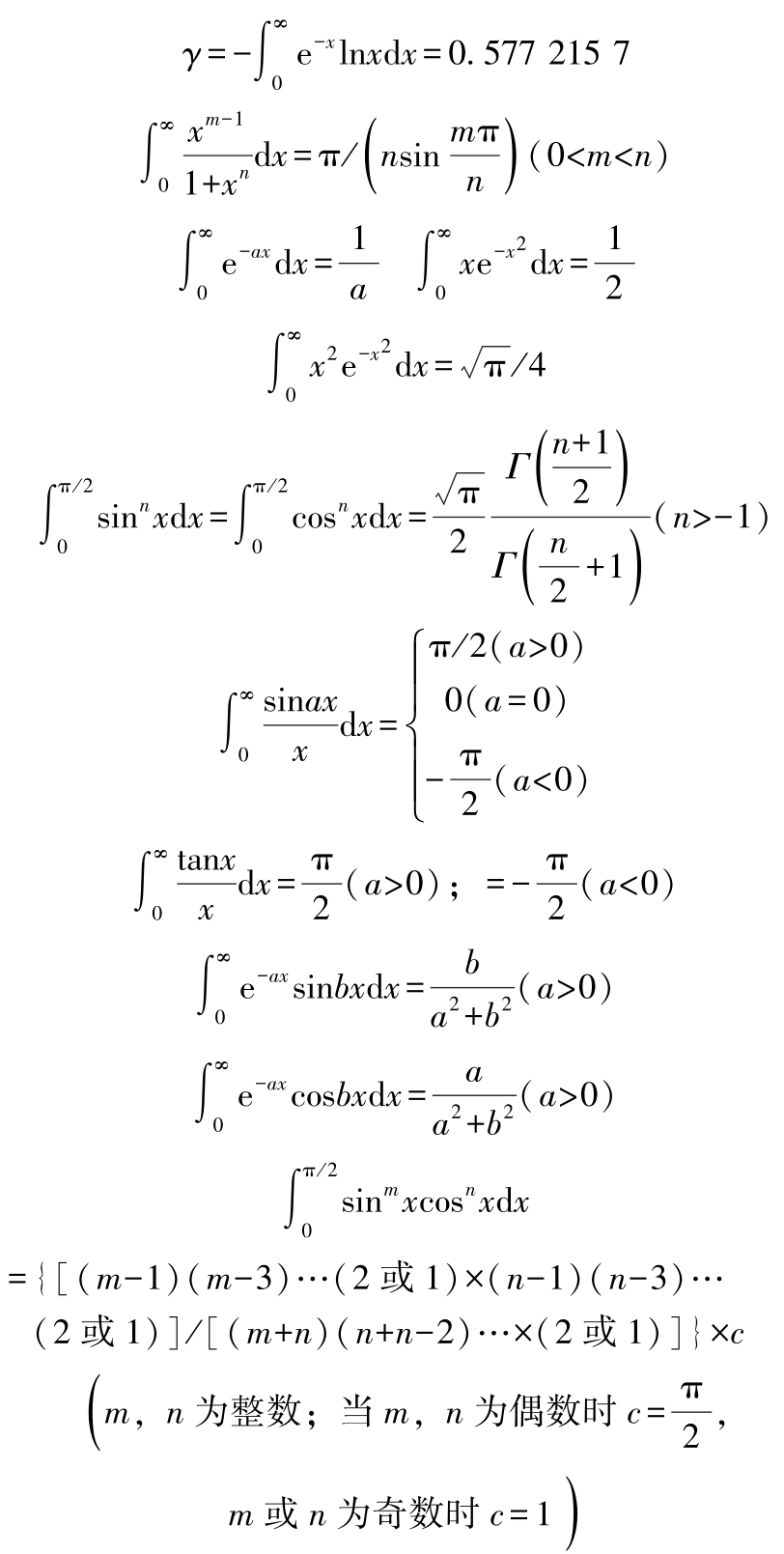
♣MATLAB中函数的不定积分:int
格式:yy=int(f)求函数f对默认变量的不定积分,用于函数只有一个变量。
yy=int(f,v)求函数f对变量v的不定积分。
♣MATLAB中函数的定积分:int
格式:yy=int(f,x,a,b)用微积分基本公式计算定积分
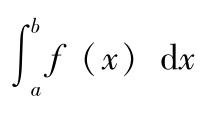 。
。
(1)泰勒级数与马克劳林级数 当
n
无穷增加时,若
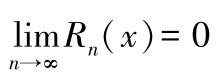 ,函数
f
(
x
)展开成无穷幂级数
,函数
f
(
x
)展开成无穷幂级数
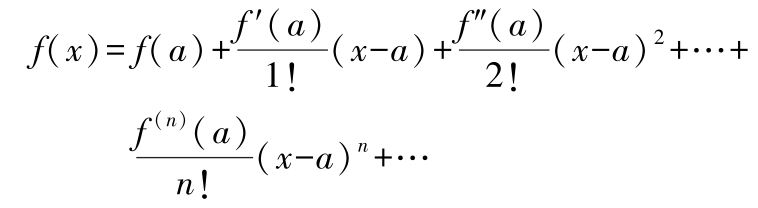
称为泰勒级数。同样,当 a =0时,有马克劳林级数
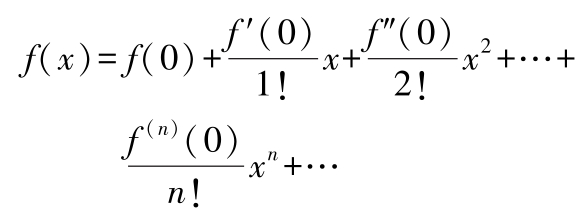
(2)几种重要函数的幂级数见表1.4-2。
♣MATLAB中函数的泰勒级数与马克劳林级数:taylor
格式:yy=taylor(f)将函数f展开成默认变量的6阶马克劳林级数。
yy=taylor(f,n)将函数f展开成默认变量的n阶马克劳林级数。
yy=taylor(f,n,v,a)将函数f(v)在v=a展开成n阶泰勒级数。
表1.4-2 几种重要函数的幂级数
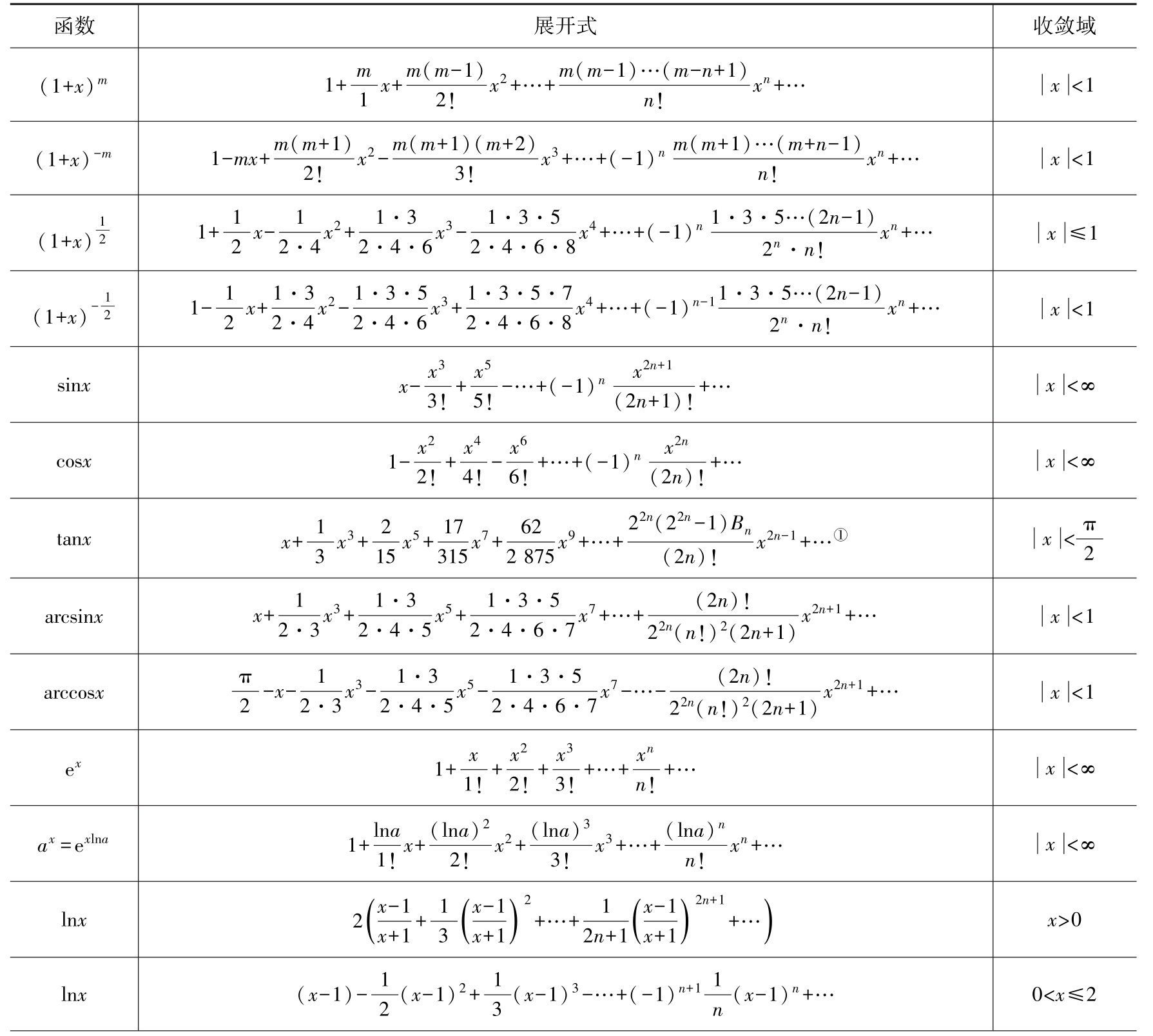
(续)
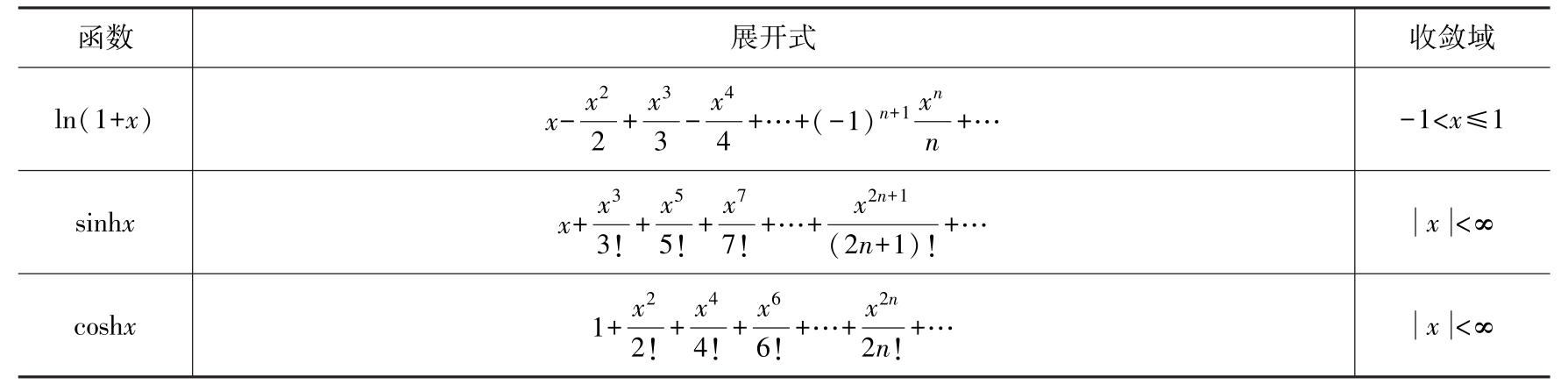
①
B
n
为伯努利系数,由下式确定:
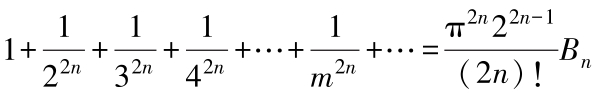
(1)傅里叶级数 满足关系式
f
(
x
+
T
)=
f
(
x
)的函数
f
(
x
)是周期为
T
的周期函数。若周期函数
f
(
x
)在区间上满足下列狄利克莱(Dirichlet)条件:1)连续或者只有有限个第一类间断点(在这种间断点,函数的跃变值有限);2)只有有限个极值点,则
f
(
x
)在区间
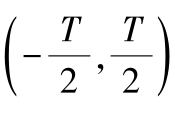 可以展开成傅里叶级数:
可以展开成傅里叶级数:
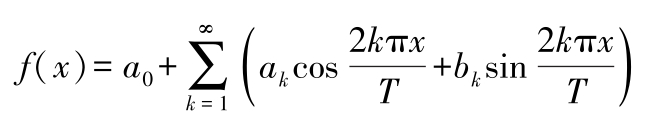
式中 a k 和 b k ——傅里叶系数。利用正交函数的性质,可得傅里叶系数的计算公式:
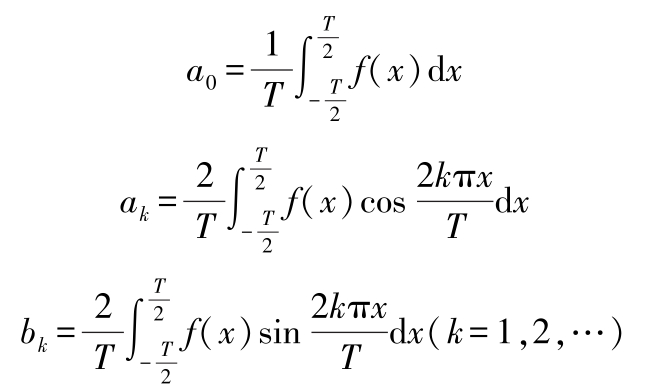
定义在有限区间( O , P )上的函数(在区间“ OP ”之外无定义) f ( x ),不考虑是否是周期性的,可以在区间( -P , O )上延拓,按不同方式来定义。
(2)几种常见的函数的傅里叶级数
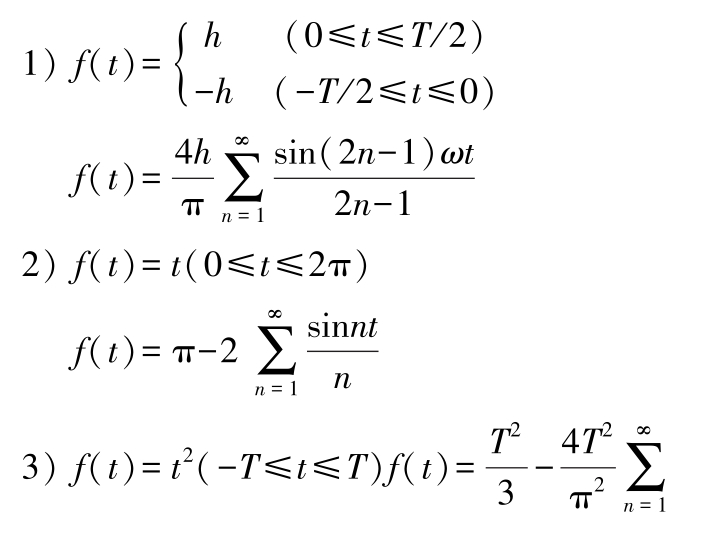
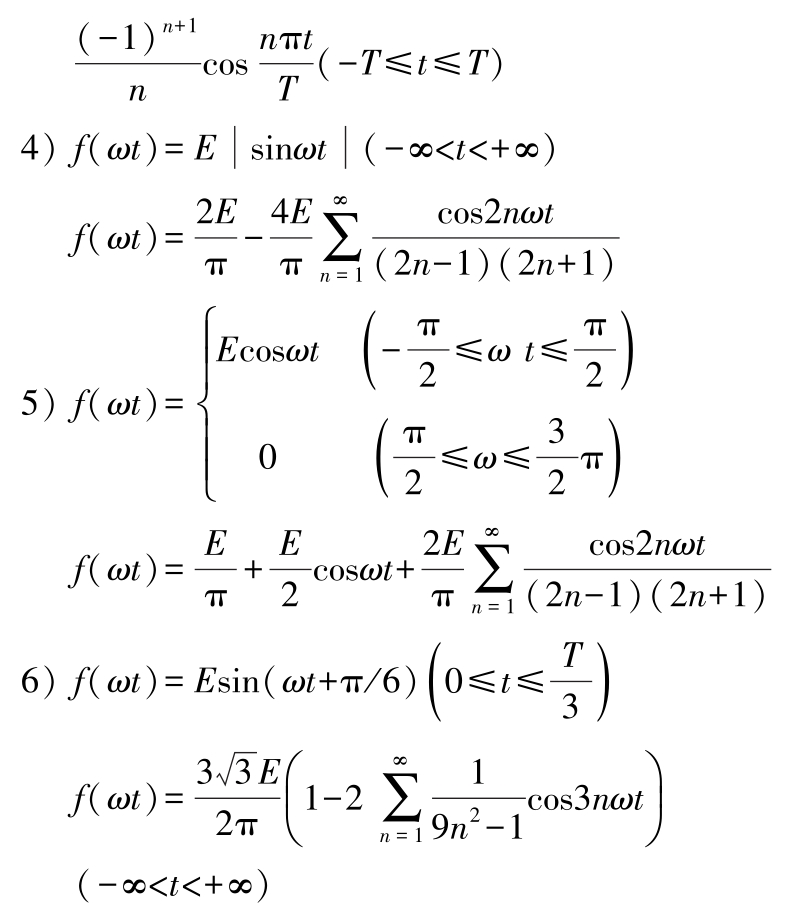
(3)傅里叶变换(傅氏变换) 若非周期函数
f
(
t
)在(-∞,+∞)上绝对可积,即广义积分
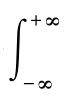
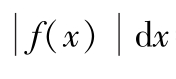 =有限值,则函数
f
(
t
)的傅氏变换为
=有限值,则函数
f
(
t
)的傅氏变换为
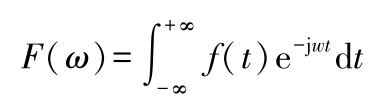
F ( ω )的逆变换为
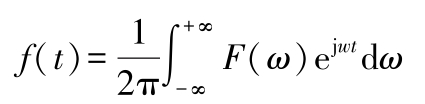
若 f ( t )是偶函数,则 F ( ω )变为傅氏余弦变换:
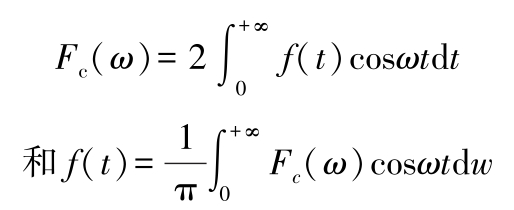
若 f ( t )是奇函数,则 F ( ω )变为傅氏正弦变换:
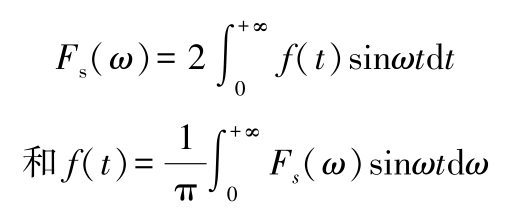
(4)傅氏变换的卷积定理 若 F ( ω ), G ( ω )是 f ( t ), g ( t )的傅氏变换,则 F ( ω ) G ( ω )为 f 和 g 的卷积变换:
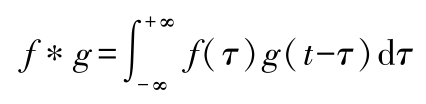
♣MATLAB中傅里叶变换与逆变换函数:fourier和ifourier
格式:Fw=fourier(ft,t,w)求“时域”函数ft的Fourier变换Fw。
ft=ifourier(Fw,w,t)求“频域”函数Fw的Fourier反变换ft。
说明:ft是以 t 为自变量的“时域”函数;Fw是以圆频率 ω 为自变量的“频域”函数。
(1)拉氏变换对 拉氏变换:设
f
(
t
)是实变数
t
(
t
>0)的函数,并且,当
t
<0时
f
(
t
)=0;它是连续函数或分段连续函数;
f
(
t
)是指数级的,即当
t
>
T
(
T
为某一相当大正数)时,
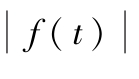 ≤
M
e
at
,
M
、
a
是实常数,则
≤
M
e
at
,
M
、
a
是实常数,则
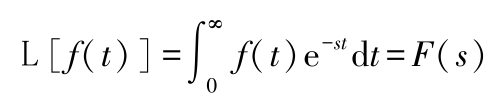
称为拉氏变换;其中 f ( t )称为原函数, F ( s )称为象函数。
相应的有拉普拉斯逆变换式(拉普拉斯变换的反演公式):
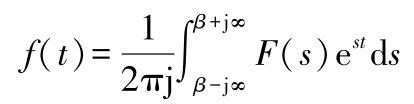
此式亦简称拉氏逆变换式(或拉氏逆变换)。记为
f ( t )= L -1 [ F ( s )]
式中 F ( s )称为 f ( t )的象函数, f ( t )则称为 F ( s )的原函数。象函数和相应的原函数构成拉氏变换对。
为了照顾电路和系统可能在 t =0时有冲激信号 Aδ ( t )存在,拉氏变换的积分下限应取0 -, f ( t )的定义域也应从0 -到 ∞,这样就能把冲激 δ ( t )包括进去,即拉氏变换式应为
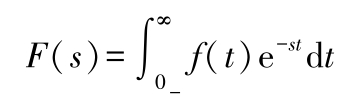
(2)拉氏变换的若干性质和定理见表1.4-3。
(3)拉氏变换简表见表1.4-4。
表1.4-3 拉氏变换的若干性质和定理
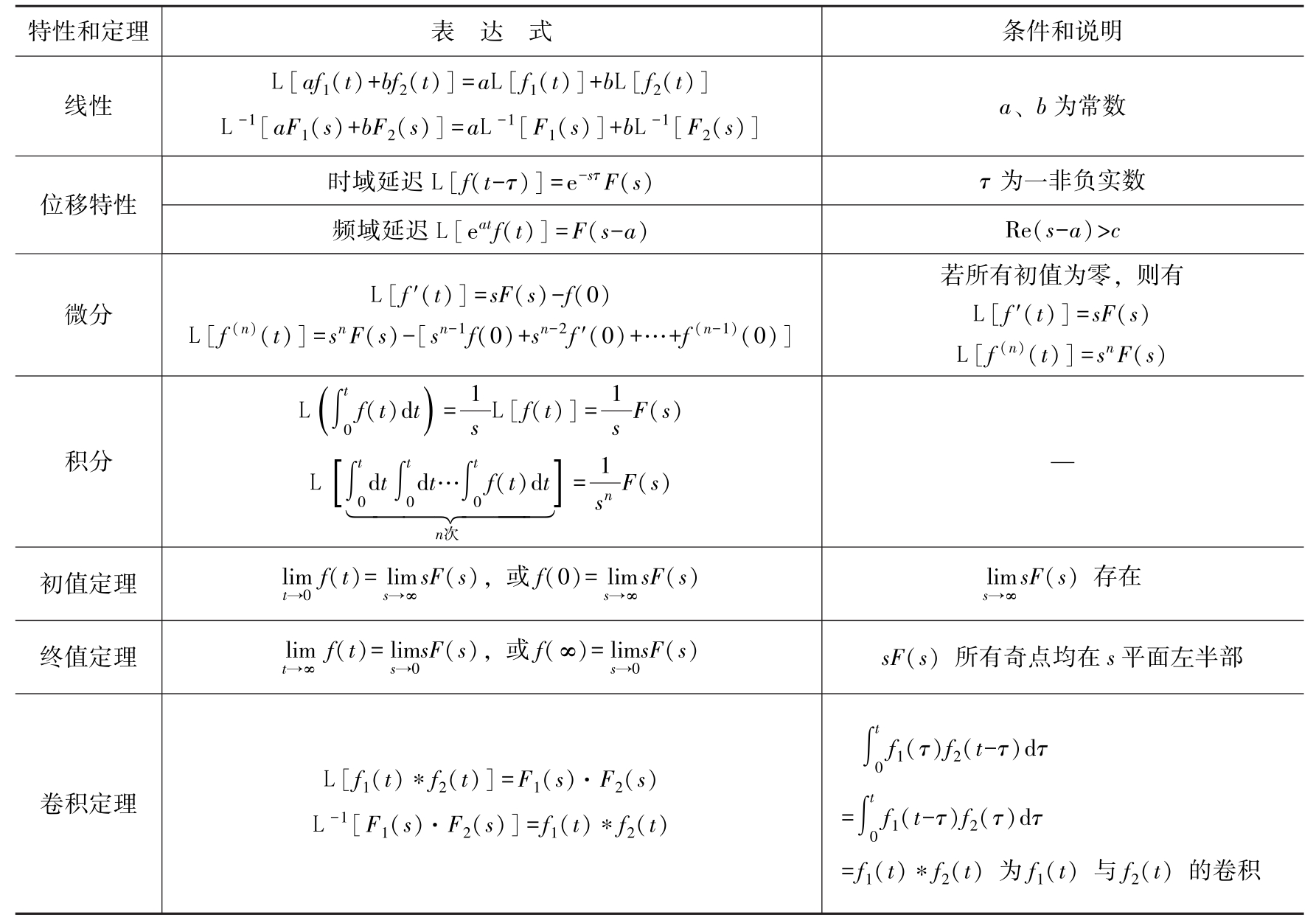
表1.4-4 拉氏变换简表

(4)用部分分式法求拉氏逆变换(海维赛德展开定理) 计算拉氏逆变换的基本方法是部分分式法,即将 F (s)展开成部分分式,成为可在拉氏变换表中查到的 s 的简单函数,然后通过反查拉氏变换表求取原函数 f ( t )。
设 F ( s )= F 1 ( s ) /F 2 ( s ), F 1 ( s )的阶次不高于 F 2 ( s )的阶次,否则,用 F 2 ( s )除以 F 1 ( s )得到一个 s 的多项式与一个余式之和。下面是三种基本的部分分式展开式
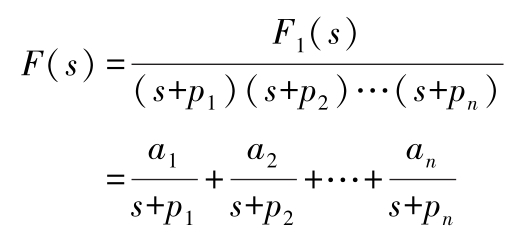
当 p 1 和 p 2 为共轭复数极点时:
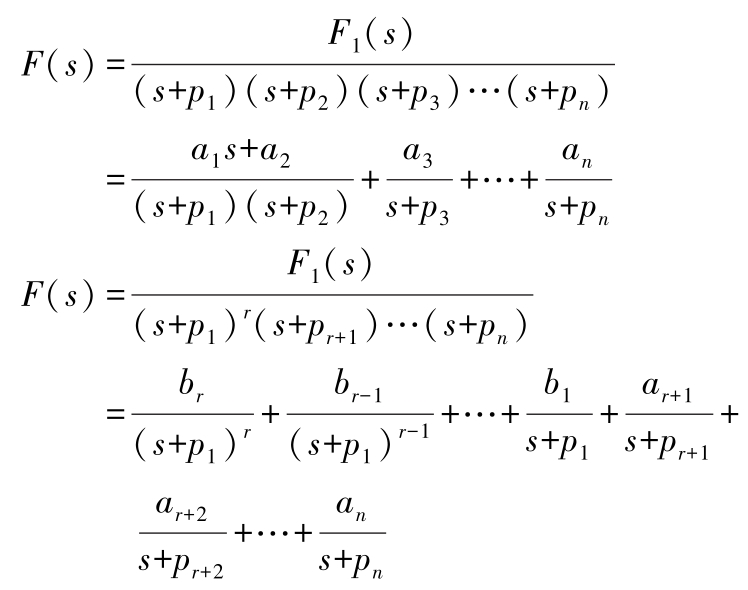
式中 a 1 , a 2 ,…, a r +1 , a r +2 …, a n 和 b r , b r -1 ,…, b 1 为常数。为了确定这些常数,用 F 2 ( s )的一个因子( s + p k )乘以 F 1 ( s ) /F 2 ( s )及其展开式的各项( k =1,2,……, n ),所得的恒等式对所有 s 的值都成立,相继令 s = -p k ,即可一一确定各常数。
♣MATLAB中拉普拉斯变换与逆变换函数:
laplace和ilaplace
格式:Fs=laplace(ft,t,s)求“时域”函数ft的Laplace变换Fs。
ft=ilaplace(Fs,s,t)求“频域”函数Fs的Laplace反变换ft。
说明:ft是以t为自变量的“时域”函数;Fs是以复频率s为自变量的“频域”函数。
(1) Z 变换 连续信号被采样后就得出离散函数,处理这类函数应用 z 变换法。它在离散系统中所起的作用犹如拉氏变换之于连续系统。设 z =e sT , Z 变换的定义为
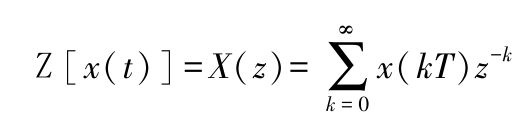
(2) Z 变换表见表1.4-5。
表1.4-5 Z 变换表

(续)

♣MATLAB中 Z 变换与逆变换函数:ztrans和iztrans
格式:FZ=ztrans(fn,n,z)求“时域”序列fn的 Z 变换FZ。
fn=iztrans(FZ,z,n)求“频域”序列FZ的 Z 反变换fn。
说明:fn是以n为自变量的“时域”序列;FZ是以z为自变量的“频域”序列。
m × n 阶矩阵记作( a ij ) m × n 或 A m × n ,简记为 A ,即
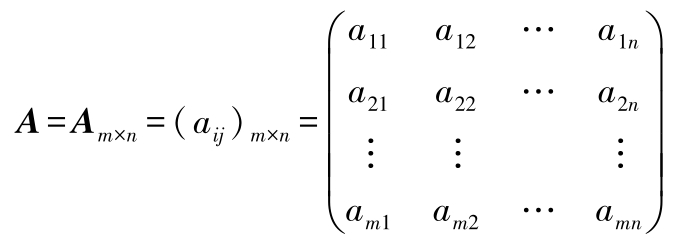
若 m = n , A 称为 n 阶方阵。
♣MATLAB中矩阵的定义:在MATLAB中不必说明矩阵的维数和类型,它们是由输入数据的类型、格式和内容来确定的,MATLAB会自动获取所需的空间。输入小矩阵最简单的方法是使用直接排列的形式,即把矩阵的元素直接排列到方括号“[]”中,每行内的元素用空格或逗号隔开,行与行之间用分号隔开。大矩阵可以分行输入,用回车键代替分号。
(1)方阵
A
的迹和轶
n
阶方阵
A
所有主对角元之和,称为
A
的迹。记作
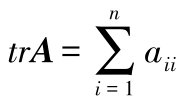 。
。
若
n
阶方阵
A
的
n
个列向量中有
r
个线性无关(
r
≤
n
),而所有个数大于
r
的列向量都线性相关,则称数
r
为矩阵
A
的列秩,类似可定义矩阵
A
的行秩。矩阵
A
的列秩和行秩一定相等,亦称之为矩阵
A
的秩,记作rank
A
=
r
,如果
r
=
n
,则称满秩,必有
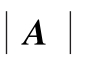 ≠0,故非奇异方阵为满秩矩阵,简称满阵。若
r
<
n
,则称
A
为降秩矩阵,即是奇阵。
≠0,故非奇异方阵为满秩矩阵,简称满阵。若
r
<
n
,则称
A
为降秩矩阵,即是奇阵。
♣MATLAB中矩阵的迹函数:trace
格式:b=trace( A )返回矩阵 A 的迹,即 A 的对角线元素之和。
♣MATLAB中矩阵的秩函数:rank
格式:k=rank( A )求矩阵 A 的秩。
k=rank( A ,tol)tol为给定误差。
(2)矩阵的代数运算和MATLAB中的矩阵运算见表1.4-6、表1.4-7。
表1.4-6 矩阵的几种代数运算法则

(续)

表1.4-7 MATLAB中矩阵的基本运算

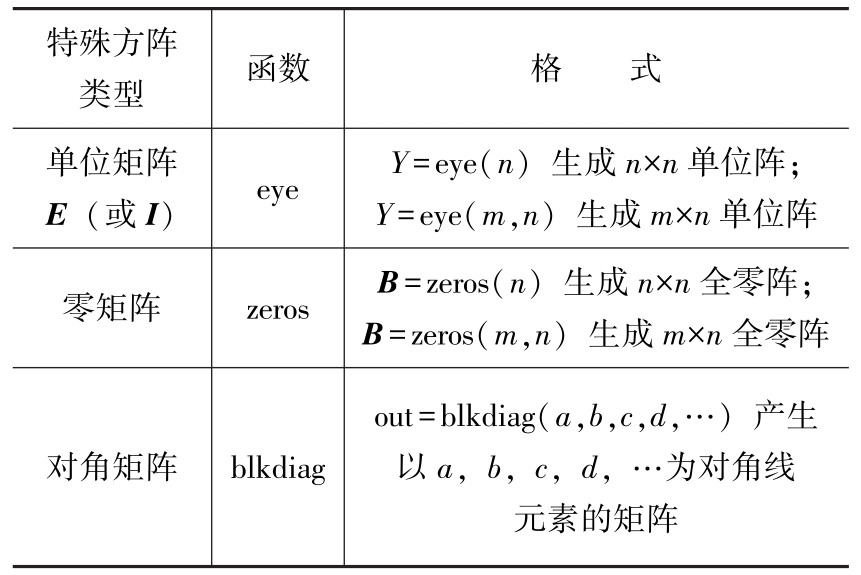
(3)一些特殊方阵和MATLAB中的一些特殊方阵的定义见表1.4-8、表1.4-9。
表1.4-8 一些特殊方阵 [12]

表1.4-9 MATLAB中一些特殊方阵的定义
(4)矩阵的特征值、特征向量和特征方程 对 n 阶方阵 A 和 n 维列向量 a ,如有一个数 λ ,使得 A a = λa ,则称 λ 为矩阵 A 的特征值(特征根), a 为 A 的特征值 λ 所对应的特征向量。
A
-λ
I
称为特征矩阵。
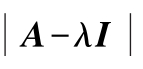 称为矩阵
A
的特征多项式。
称为矩阵
A
的特征多项式。
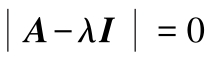 则称为
A
的特征方程。特征方程的
n
个根
λ
1
、
λ
2
、…、
λ
n
就是矩阵
A
的
n
个特征值(亦称本征值)。集合{
λ
1
,
λ
2
,…,
λ
n
}称为
A
的谱,记作ch
A
。
则称为
A
的特征方程。特征方程的
n
个根
λ
1
、
λ
2
、…、
λ
n
就是矩阵
A
的
n
个特征值(亦称本征值)。集合{
λ
1
,
λ
2
,…,
λ
n
}称为
A
的谱,记作ch
A
。
♣MATLAB中矩阵的特征多项式函数:poly
格式:p=poly( A )求矩阵 A 的特征多项式系数P。
♣MATLAB中矩阵的特征值、特征向量函数:eig
格式:d=eig( A )求矩阵 A 的特征值 d ,以向量形式存放 d 。
[V,D]=eig( A )计算 A 的特征值对角阵 D 和特征向量 V ,使 AV = VD 成立。
(1)矩阵的导数 如矩阵 A 的元素 a ij 都是变量 t 的函数,则 A 对 t 的一阶导数定义为
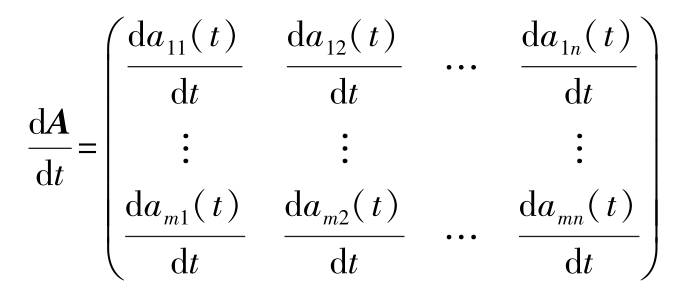
同样可定义矩阵的高阶导数
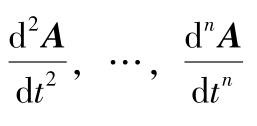 等(设各元素对
t
高阶可微)。
等(设各元素对
t
高阶可微)。
(2)矩阵的积分 矩阵 A 的积分定义为
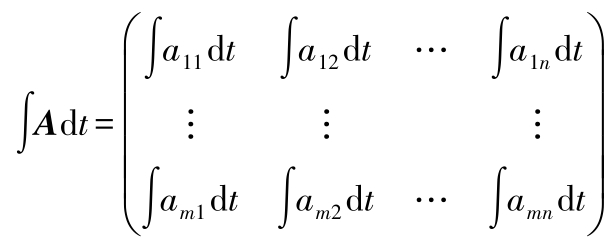
同样可定义矩阵的多重积分。
(3)矩阵求逆 若 A 、 B 二阵满足等式
AB = I (单位阵)
则称 A 为 B 的逆矩阵,或称 B 为 A 的逆矩阵。记作
A = B -1 或 B = A -1
A 的逆阵 A -1 按下式算出:
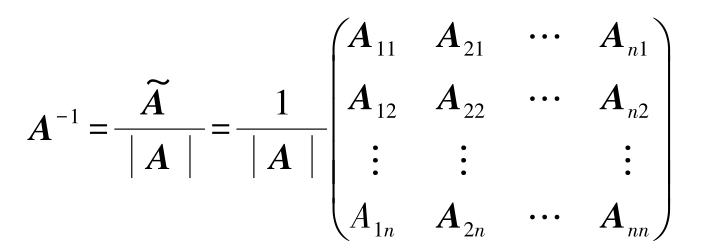
式中,
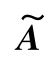 称为
A
的伴随矩阵(或附加矩阵),它的第
i
行第
j
列元素是
称为
A
的伴随矩阵(或附加矩阵),它的第
i
行第
j
列元素是
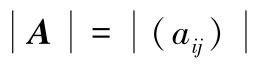 的第
j
行第
i
列元素的代数余子式。例如
A
的伴随矩阵
的第
j
行第
i
列元素的代数余子式。例如
A
的伴随矩阵
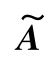 第1行第2列的元素
A
21
是
|A|
中元素
a
21
的代数余子式。
第1行第2列的元素
A
21
是
|A|
中元素
a
21
的代数余子式。
矩阵 A 可逆的充要条件是det A = |A| ≠0,即 A 为非奇异方阵。
♣MATLAB中矩阵的逆矩阵函数:inv
格式:Y=inv( A )求方阵 A 的逆矩阵。
若 A 为奇异矩阵或近似奇异矩阵,将给出警告信息。
(4)矩阵的相似变换和正交变换
1)相似变换 设 A 、 B 是两个 n 阶矩阵,如有 n 阶满秩矩阵 Q 存在,使得
B = Q -1 AQ
则称矩阵 A 与矩阵 B 相似,或称 A 经过相似变换 Q -1 AQ 化为 B ,记作 B ~ A 。
2)正交变换 若有正交矩阵 Q 存在:
Q -1 = Q T
则称 Q T AQ = Q -1 AQ 为矩阵 A 的正交变换。
Δ 为算子(DEL OPERATOR):
算子
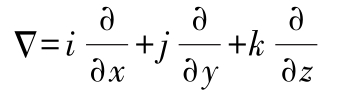
梯度
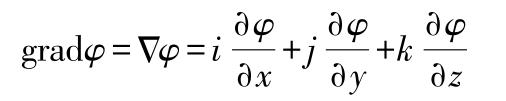
散度
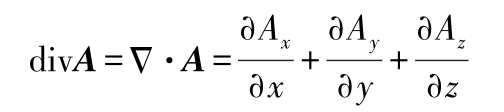
旋度
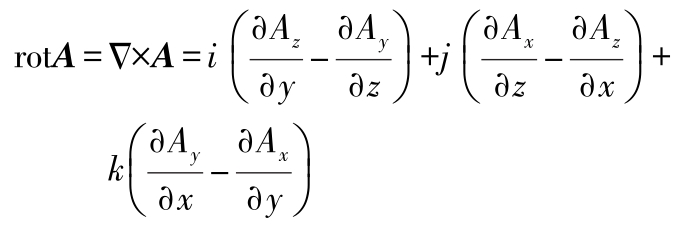
(1)有关Δ 的公式(假定 A 、 B 、 U 和 V 的偏导数存在)
Δ( U + V )=Δ U +Δ V
Δ·( A + B )=Δ· A +Δ· B
Δ×( A + B )=Δ× A +Δ× B
Δ·( U A )=(Δ U )· A + U (Δ· A )
Δ×( U A )=(Δ U )× A + U (Δ× A )
Δ·( A × B )= B ·(Δ× A ) -A ·(Δ× B )
Δ×( A × B )=( B ·Δ) A ) -B (Δ· A )-( A ·Δ) B + A (Δ· B )
Δ( A · B )=( B ·Δ) A +( A ·Δ) B + B ×(Δ× A )+ A ×(Δ× B )
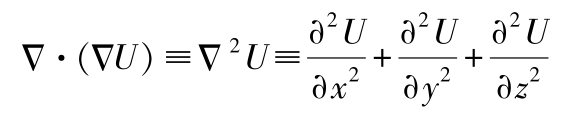
Δ×(Δ U )=0 Δ·(Δ× A )=0
Δ×(Δ× A )=Δ(Δ· A )-Δ 2 A
(2)球面坐标的梯度、散度和旋度(单位矢量 u r , u φ , u z )
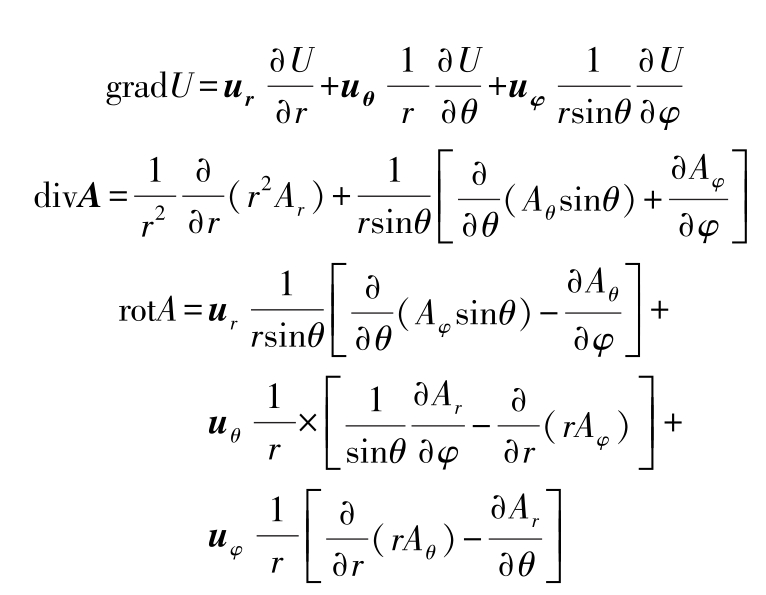
(3)柱面坐标的梯度、散度和旋度(单位矢量 u r , u φ , u z )
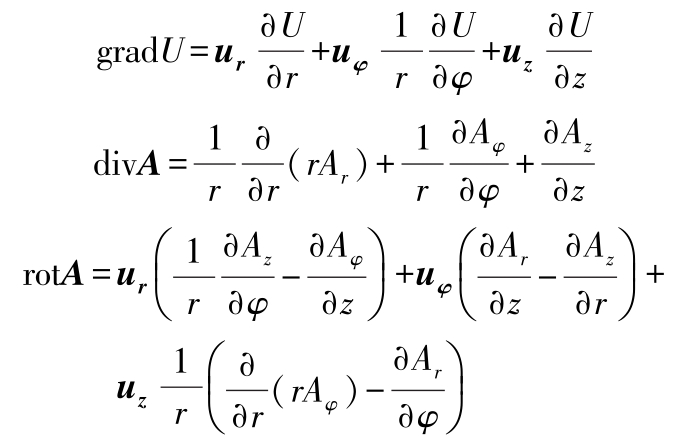
(4)高斯定理
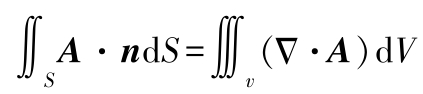
式中 n ——闭曲面外法向单位矢量;
S ——闭曲面。
(5)斯托克定理
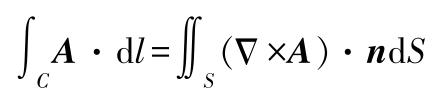
式中 C ——闭曲线;
d l——C 的微小长度矢量;
n——S 面的法线单位矢量;
S ——以 C 为边界的面。
n 和 C 的方向形成右手系。
♣MATLAB中求梯度函数:gradient,jacobian
格式:[FX,FY]=gradient(F,h)求二元函数的梯度,FX、FY分别是二元函数的
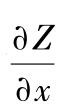 、
、
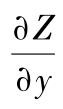 。
。
[FX,FY,FZ,…]=gradient(F,h1,h2,h3,…)求多元函数的梯度。
GRAD=jacobian(f)求函数f的梯度。
说明:1)gradient用于求解数值梯度,F是函数的数值矩阵;h是函数沿坐标取点的步长,而h1,h2,h3等分别表示沿x,y,z等方向的不同步长。步长可以缺省,缺省时,默认步长为1;输出FX,FY,FZ分别表示沿x,y,z方向的偏导数。2)jacobian用于求解表达式形式的梯度,f是关于自变量的函数表达式,输出GRAD是沿x,y,z方向的偏导数组成的矩阵。
(1)概率在相同条件下重复进行 n 次试验,当 n 充分大时,若 A 发生的频率 f n ( A )越来越趋近于 p ,则称 p 为此试验中随机事件 A 发生的概率,简称事件 A 的概率。记作
P ( A )= p
对于任何事件
A
,均有
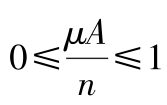 ,由定义,有
,由定义,有
0≤ P ( A )≤1
显然, P ( Q )≡1, P (⌀)≡0。
概率的简单性质:若必然事件记作 U ,不可能事件记作 V ,则
P ( U )=1, P ( V )=0,0≤ P ( A )≤1;
若
A
⊂
B
(事件
B
包含事件
A
),则
P
(
A
)≤
P
(
B
)若
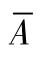 是
A
的对立事件,则
是
A
的对立事件,则
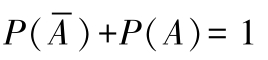
(2)概率的基本运算 概率加法定理:
P ( A + B )= P ( A )+ P ( B ) -P ( AB )
式中 A + B ——事件 A 、 B 至少有一个发生;
AB ——事件 A 与事件 B 同时发生。
若事件 A 与事件 B 互斥: AB = V ,则事件 A + B 的概率:
P ( A + B )= P ( A )+ P ( B )
若
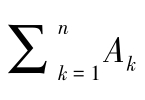 =
U
,
A
i
A
j
=
V
(
i
≠
j
),则
=
U
,
A
i
A
j
=
V
(
i
≠
j
),则
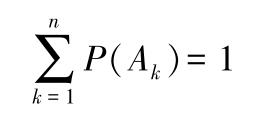
条件概率:在事件
A
出现的条件下事件
B
出现的概率,记作
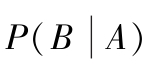 ,其计算式为
,其计算式为
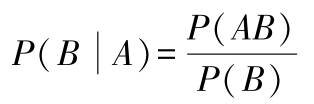
概率乘法定理:
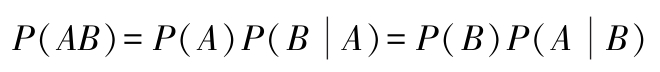
对于独立事件,则事件 A 与 B 同时发生的概率为
P ( AB )= P ( A ) P ( B )
对于概率相同的
n
个独立事件的积事件
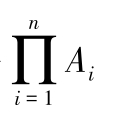 的概率为
的概率为
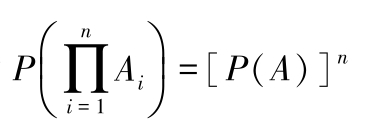
(1)随机变量的分布函数随机变量的取值小于某一数 x 的概率是 x 的函数时,称为此随机变量的分布函数。由它可决定随机变量落入在 x 的任何范围内的概率。分布函数分离散型(例如二项分布、泊松分布)和连续型(例如正态分布)两类。
正态分布:一般地说,如果研究的某个量是被彼此间相互独立的大量偶然因素所影响,且每一因素在总的影响中只起很小的作用,则由这个总的影响所引起的该量的变化,就近似地服从正态分布,记作 N ( μ , σ 2 )。正态分布的密度函数为
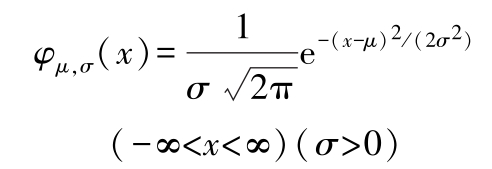
式中, μ 、 σ ( σ >0)为常数。
正态分布的分布函数为
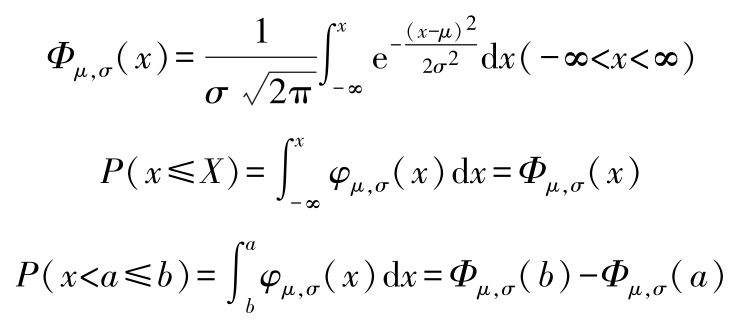
正态分布的密度函数 φ ( x )和分布函数 Φ ( x )的图形见图1.4-1和图1.4-2。
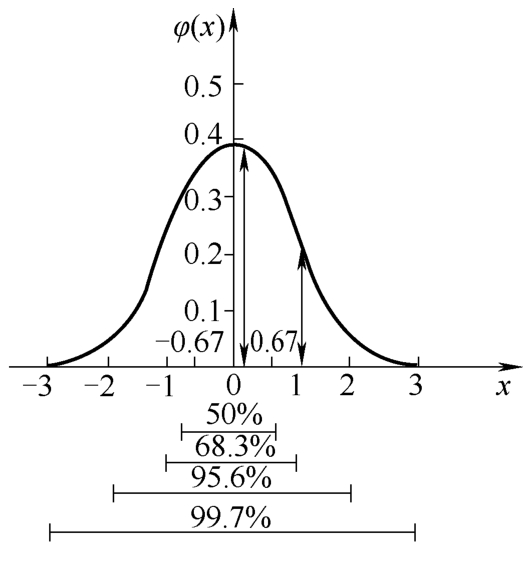
图1.4-1 正态密度函数 φ ( x )
横坐标下第四横线表示:在(-3,3)中,曲线下的面积是99.7%,其他横线意义类似
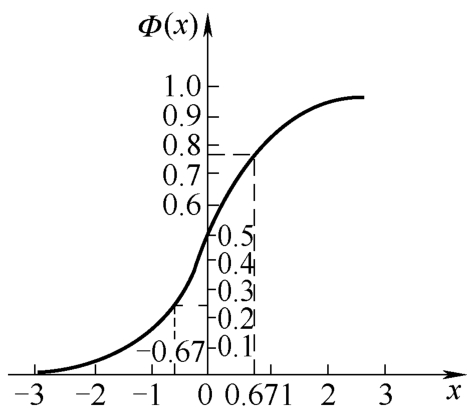
图1.4-2 正态分布函数 Φ ( x )
(2)数字特征(见表1.4-10)
表1.4-10 随机变量的数字特征

♣MATLAB中采用通用函数计算概率密度函数值:pdf
格式:Y=pdf(‘name’,K,A)
Y=pdf(‘name’,K,A,B)
Y=pdf(‘name’,K,A,B,C)
说明:返回在X=K处,参数A、B、C的概率密度值,对于不同的分布,参数个数是不同的;name为分布函数名,如‘beta’表示Beta分布,‘bino'表示二项分布,‘exp’表示指数分布,‘f’表示F分布等。
♣MATLAB中采用通用函数计算分布函数值:cdf
格式:Y=cdf(‘name’,K,A)
Y=cdf(‘name’,K,A,B)
Y=cdf(‘name’,K,A,B,C)
说明:返回以name为分布,随机变量 X ≤ K 的概率之和的累积概率值,即分布函数值。对于不同的分布,参数个数是不同的;name为分布函数名,如‘beta’表示Beta分布,‘bino'表示二项分布,‘exp’表示指数分布,‘f’表示F分布等。
♣MATLAB中随机变量的数学期望、方差和标准差函数:mean,var,std
格式:Y=mean(X)X为向量,返回X的平均值,即数学期望。
D=var( X )
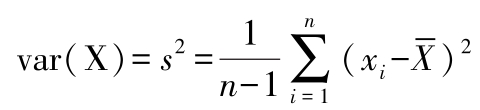
若X为向量,则返回向量的样本方差。
D=var(A)A为矩阵,则D为A的列向量的样本方差构成的行向量。
D=var(X,1)返回向量(矩阵)X的简单方差(即置前因子为
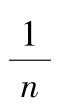 的
方差)。
的
方差)。
D=var(X,w)返回向量(矩阵)X的 以w为权重的方差。
D=std(X)返回向量(矩阵)X的样本标准差(置前因子为
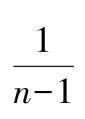 ),
),
即
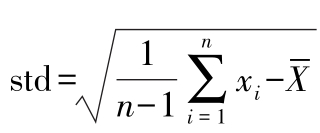 。
。
D=std(X,1)返回向量(矩阵)X的标准差(置前因子为
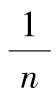 )
)
D=std(X,0)与std(X)相同。
D=std(X,flag,dim)返回向量(矩阵)维数为dim的标准差值,
式中 flag=0时,置前因子为
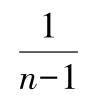 ,
否则置前因子为
,
否则置前因子为
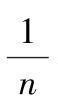 。
。
(1)抽样方法 根据判断标准,首先确定抽样属于计数值还是计量值,分为计数抽样检验和计量抽样检验。每种抽样检验又分为一次抽样检验、二次抽样检验、多次抽样检验和序贯抽样检验。
(2)总体(母体)与样本(随机样本、子样) 研究某个问题,它的对象的所有可能观察结果的全体称为总体(或称母体),记作 X 。总体中的每个元素称为个体。从总体 X 中任意抽出的部分个体,称为总体的一个随机样本,简称样本(或子样)样本中含有个体的个数称为样本的大小(或容量)。
(3)抽样分布、统计量 样本是随机变量,是进行统计判断的依据,它的函数也是随机变量。如 X 1 , X 2 ,…, X n 是来自总体 X 的一个样本, g ( X 1 , X 2 ,…, X n )是 X 1 , X 2 ,…, X n 的函数,且 g 中不含任何未知参数,则称 g ( X 1 , X 2 ,…, X n )是一个统计量。如 x 1 , x 2 ,… x n 是相应于样本 X 1 , X 2 ,…, X n 的样本值,即样本的观察值,则可定义几个统计量见表1.4-11所示。
表1.4-11 几种常用的统计量

(续)

(1)参数估计 [18,19] 如总体 X 的分布函数的形式为已知,但它的一个或多个参数为未知,根据来自母体 X 的一个样本 X 1 , X 2 ,…, X n ,对未知参数 θ 的值进行估计称为参数估计。
1)点估计 是求某一个参数的估计值。当总体
X
的分布函数
F
(
x
,
θ
)的形式为已知,其中有待估参数
θ
,
X
1
,
X
2
,…,
X
n
是
X
的一个样本,
x
1
,
x
2
,…
x
n
是相应的样本值。点估计就是要构造一个适当的统计量
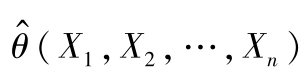 ,用它的观察值
,用它的观察值
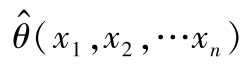 作为未知参数
θ
的估计值。常用构造估计量的方法有矩估计法和极大似然估计法两种,具体步骤见参考文献[9,20]。
作为未知参数
θ
的估计值。常用构造估计量的方法有矩估计法和极大似然估计法两种,具体步骤见参考文献[9,20]。
2)区间估计 是要估计参数的一个范围,以及这个范围包含参数 θ 真值的可信程度。这样的范围通常以区间的形式给出,所以称为区间估计。这样的区间即所谓的置信区间。
♣MATLAB中参数估计函数表见表1.4-12。
表1.4-12 MATLAB中参数估计函数表

(续)

说明:各函数返回已给数据向量X的参数最大似然估计值和置信度为(1-a)×100%的置信区间。a的默认值为0.05,即置信度为95%。
(2)假设检验(统计检验) 在总体的分布函数完全未知或只知其形式,但不知其参数的情况下,为了推断总体的某些性质,提出某些关于总体的假设。
采用一个合理的法则,对假设作出判断,认为适当则接受,不适当则拒绝,所以接受假设H 0 ,即拒绝假设H 1 ,或者反之。
♣MATLAB中假设检验所用函数:
(1)功能:一个正态总体,方差 σ 2 已知时,均值 μ 的检验
函数:ztest
格式:[h,p,ci]=ztest(x,mu,sigma,alpha,tail)
式中 h——h=0表示接受H 0 ,h=1表示拒绝H 0 ;
p——在假设H 0 下样本均值出现的概率;
ci ——μ 0 的置信区间;
x——样本;
mu——H 0 中的 μ 0 ;
sigma——总体标准差 σ ;
alpha——显著性水平a(缺省时为0.05);
tail——备择假设H 1 的选择(H 1 为 μ > μ 0 时tail=1,H 1 为 μ < μ 0 时tail=-1,H 1 为 μ ≠ μ 0 时tail=0(可缺省))。
(2)功能:方差 σ 2 未知时,均值 μ 的检验
函数:ttest,ttest2
格式:[h,p,ci]=ttest(x,mu,alpha,tail)
说明:一个正态总体,方差 σ 2 未知时,均值 μ 的检验。与上面的ztest相比,除了不需输入总体标准差 σ 外,其余全部一样。
格式:[h,p,ci]=ttest2(x,y,alpha,tail)
说明:两个正态总体,方差
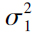 ,
,
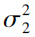 未知时,均值
μ
1
=
μ
2
的检验。与上面的ttest相比,不同之处在于输入的两个样本(长度不一定相同),其余全部一样。
未知时,均值
μ
1
=
μ
2
的检验。与上面的ttest相比,不同之处在于输入的两个样本(长度不一定相同),其余全部一样。
(1)正态概率纸 [11] 利用正态概率纸可判定某一随机变量的一批试验数据是否遵从正态分布,并可对 σ 、 μ 作出估计。
正态概率纸以各分组数据的上值为横坐标,累积频率为纵坐标分别描点。若所描出的点大致在一条直线上,则可判定此随机变量遵从正态分布。然后近似配置一条直线,此直线称回归直线。
从纵坐标刻度为50的点引一水平线与回归直线相交,此交点所对应的横坐标即为 μ 的估值;从纵坐标刻度为15.9的点引水平线与回归直线相交,此交点所对应的横坐标就是 μ 估值与 σ 估值之差,由此可算得 σ 的估值。
(2)回归分析 [11,21] 把不具有确定函数关系而只具有相关关系的变量,通过统计处理得出反映变量间关系的主流趋向曲线(回归曲线),并对实际数据偏离该曲线的程度作出概率估计。
设随机变量 y 与 x 之间存在着某种相关关系,且 x 是可以控制或可以精确观测其数值的自变量,即可认作是普通的变量。由于 y 是随机变量,对于 x 的每一个确定值, y 有它的分布。若 y 的数学期望存在,其值随 x 值而定,即 y 的数学期望是 x 的函数,记作 μ ( x ), μ ( x )称为 x 的回归。 y = μ ( x )就称为 y 关于 x 的回归函数,又称为 y 关于 x 的回归方程。
对于一元线性回归:设变量 x 和 y 的 n 次观测值为( x 1 , y 1 ),( x 2 , y 2 ),…,( x n , y n ),若 x 和 y 间存在一定的线性关系,则可用下列直线方程进行拟合:
y ^= a + bx
式中 a 、 b 可利用最小二乘法解得:
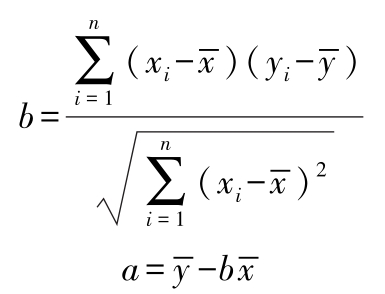
式中
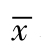 、
、
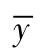 ——x
i
和
y
i
的平均值。
——x
i
和
y
i
的平均值。
一元线性回归的相关系数,两变量之间的线性关系的密切程度可用相关系数 r 表示:
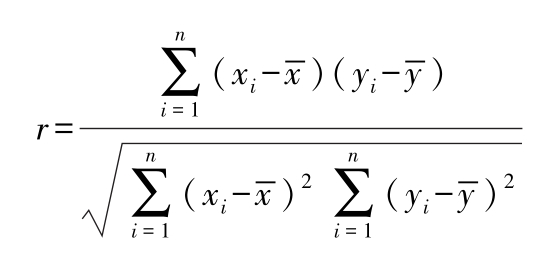
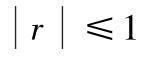 。当
。当
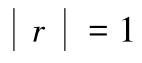 时,
x
、
y
为完全线性关系;
时,
x
、
y
为完全线性关系;
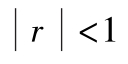 时,
x
、
y
有一定的线性关系;而
时,
x
、
y
有一定的线性关系;而
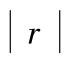 越接近于1,表示线性关系越密切;当
越接近于1,表示线性关系越密切;当
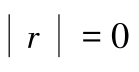 时,表示
x
、
y
间毫无线性关系。
时,表示
x
、
y
间毫无线性关系。
一元线性回归的回归线的精度,可用剩余标准离差 s 表示:
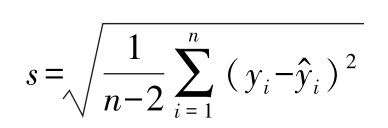
s 越小,则回归方程预报的 y 值越准确。
♣MATLAB中多元线性回归分析所用函数:regress
格式:b=regress(y,X)返回基于观测值y和回归矩阵X的最小二乘拟合 β 的结果。
[b,bint,r,rint,stats]=regress(y,X)
说明:给出 β 的估计b、 β 的95%置信区间(p*2矢量rint)、残差r以及每个残差的95%置信区间(n*2矢量rint);矢量stats给出回归的R 2 统计量和F以及p值。
格式:[b,bint,r,rint,stats]=regress(y,X,alpha)
说明:与上面的regress相比不同点在于给出的结果置信区间为100(1-alpha)%,其他都相同。
(1)设
a
是真值,
A
是近似值,则
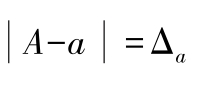 是绝对误差;
是绝对误差;
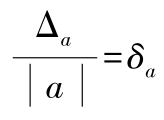 是相对误差。
是相对误差。
(2)有效数字 如果Δ a 不超过 a 的某一数位上的半个单位,那么在 a 中,从这一位往左,除去最左面第一个非零数字前的零外,所有数字都叫有效数字。
(3)几个误差计算公式(见表1.4-13)。
表1.4-13 几个误差计算公式

(续)

(4)高斯误差定律 [1] 随机误差的分布密度函数为正态型分布函数:
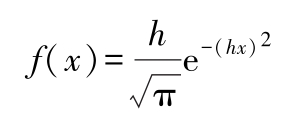
式中
h
——精密度指数,
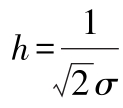 。
。
该式称为高斯误差方程,其图形称为误差曲线(见图1.4-3)。
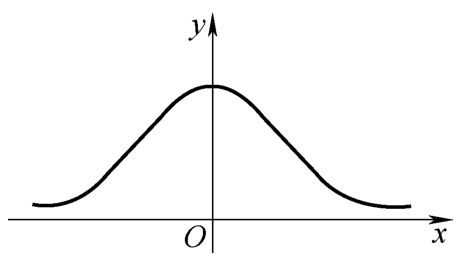
图1.4-3 误差曲线
(1)插值 若 y = f ( x )为定义在区间[ a , b ]的函数,已知 a = x 0 , x 1 , x 2 ,…, x n = b 诸点的值为 y 0 , y 1 , y 2 ,…, y n ,且有一函数满足 P ( x i )= y i ( i =0,1,2,…, n )的关系,则称 P ( x )为 f ( x )的插值函数, x 0 , x 1 , x 2 ,…, x n 称插值节点,[ a , b ]为插值区间。
一般用插值函数 P ( x )近似 f ( x ),插值函数的求法有拉格朗日(Lagrange)插值、牛顿(New-ton)插值公式、厄尔米特(Hermite)插值和三次样条插值等。
如拉格朗日插值多项式(差商插值多项式)为
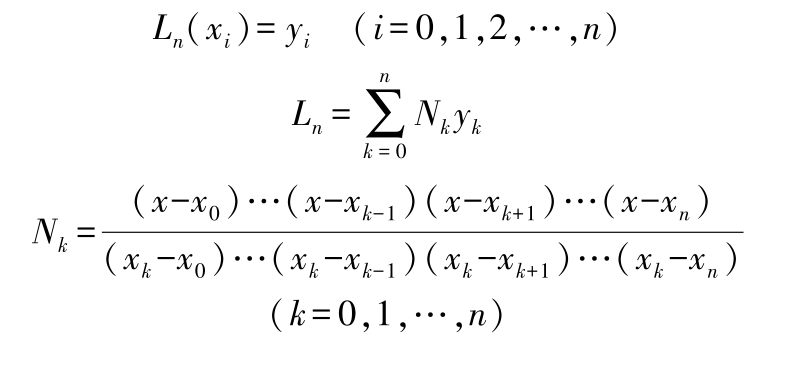
式中 N k ——节点 x 0 , x 1 ,…, x n 上的 n 次插值基函数,它们满足条件:
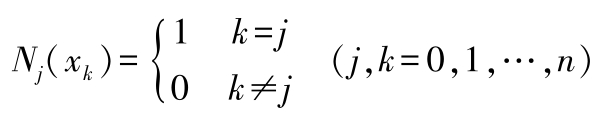
♣MATLAB中一维数据插值(表格查找)函数:interp1该命令对数据点之间计算内插值,找出一元函数 f ( x )在中间点的数值,其中函数 f ( x )由所给出数据决定。
格式:yi=interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x与Y的内插值决定。参量x指定数据Y的点。若Y为一矩阵,则按Y的每列计算。yi是阶数为length(xi)*size(Y,2)的输出矩阵。
yi=interp1(Y,xi)假定x=1:N,其中N为向量Y的长度,或者为矩阵Y的行数。
yi=interp1(x,Y,xi,method)用指定的算法计算插值:
‘nearest’:最近邻点插值,直接完成计算;
‘lnear’:线性插值(缺省方式),直接完成计算;
‘spline’:三次样条函数插值。对于该方法,命令interp1调用函数spline、ppval、mkpp、umk-PP。这些命令生成一系列用于分段多项式操作的函数。命令spline用它们执行三次样条函数插值;
‘pchip’:分段三次Hermite插值。对于该方法,命令interp1调用函数pchip,用于对向量x与y执行分段三次内插值。该方法保留单调性与数据的外形;
‘cubic’:与‘pchip’操作相同;
‘v5cubic’:在MATLAB5.0中的三次插值。
说明:对于超出x范围的xi的分量,使用方法‘nearest’,‘linear’,‘v5cubic’的插值算法,相应地返回NaN。对于其他方法,interp1将对超出的分量执行外插值算法。
yi=interp1(x,Y,xi,method,‘extrap’)对于超出x范围的xi的分量将执行特殊的外插值法extrap。
yi=interp1(x,Y,xi,method,extrapval)确定超出x范围的xi的分量的外插值法extrapval,其值经常取NaN或0。
(2)差分和差商 设函数 y = f ( x )在节点 x 0 < x 1 <…< x n (常取 x k = x 0 + kh )处取值 y 0 , y 1 ,…, y n ,即 f ( x k )= y k , k =0,1,…, n 。
一阶向前差分:Δ y k = y k +1 -y k
二阶向前差分:Δ 2 y k =Δ y k +1 -Δ y k
m 阶向前差分:Δ m y k =Δ m -1 y k +1 -Δ m -1 y k
一阶向后差分:Δ y k = y k -y k -1
m 阶向后差分:Δ m y k =Δ m -1 y k -Δ m -1 y k -1
一阶中心差分:
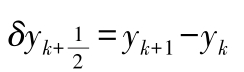
m 阶中心差分:
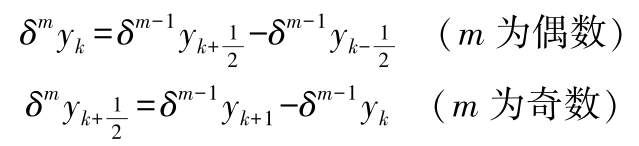
三种差分关系:
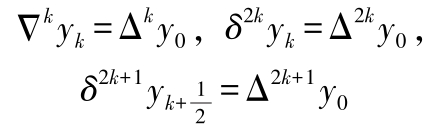
t 阶差商:
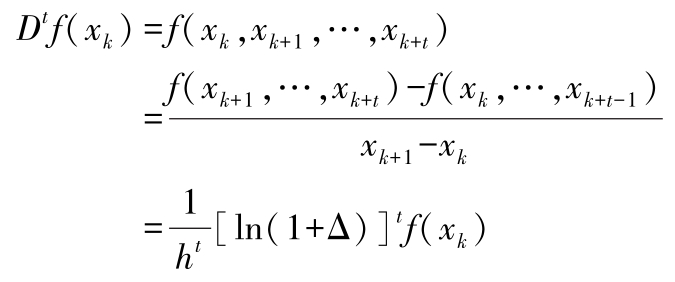
差分和差商的关系:
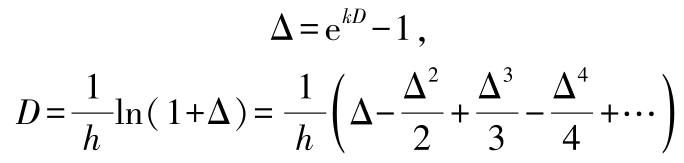
(3)经验方程 若观测到的数据是{ x i }和{ f ( x i )}, i =1,2,…,Δ x i = x i +1 -x i ,Δ y i = f ( x i +1 ) -f ( x i ),则可利用向前差分法判定经验方程的类型:
若Δ y i =定值,则方程 y = a + bx
若Δ 2 y i =定值,则方程 y = a + bx + cx 2
若Δ 3 y i =定值,则方程 y = a + bx + cx 2 + dx 3
若
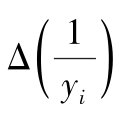 =定值,则方程
=定值,则方程
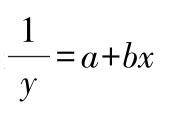
若
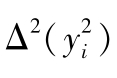 =定值,则方程
=定值,则方程
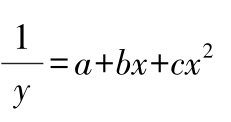
若
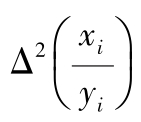 =定值,则方程
=定值,则方程
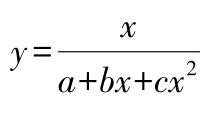
若Δ y i 成等比数列,则方程 y = ab x + c
若Δlg y i 成等差数列,则方程lg y = a + bx + cx 2
若Δ 2 y i 成等比数列,则方程 y = ab x + cx + d
(4)近似积分 近似积分法主要有根据积分中值定理的一般公式、牛顿一柯茨插值型求积公式(内插求积公式)和高斯积分法,这里主要介绍高斯积分法和一维高斯积分公式。
高斯积分法是在积分区间选择某些积分点
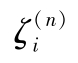 (称为高斯点),求出被积函数
f
(
x
)在高斯点的值
(称为高斯点),求出被积函数
f
(
x
)在高斯点的值
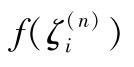 ,乘以相应的权数权因子
,乘以相应的权数权因子
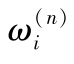 ,即求积系数,然后求总和而得积分近似值。
,即求积系数,然后求总和而得积分近似值。
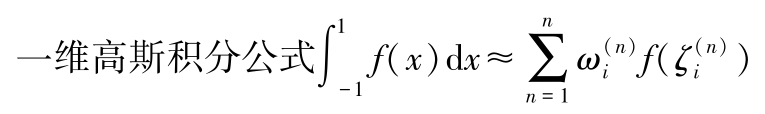
式中 n ——积分点的总数;
积分点坐标
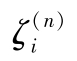 的值
——n
次勒让德多项式
P
n
(
x
)的零点。在实际计算中,
的值
——n
次勒让德多项式
P
n
(
x
)的零点。在实际计算中,
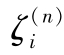 和
和
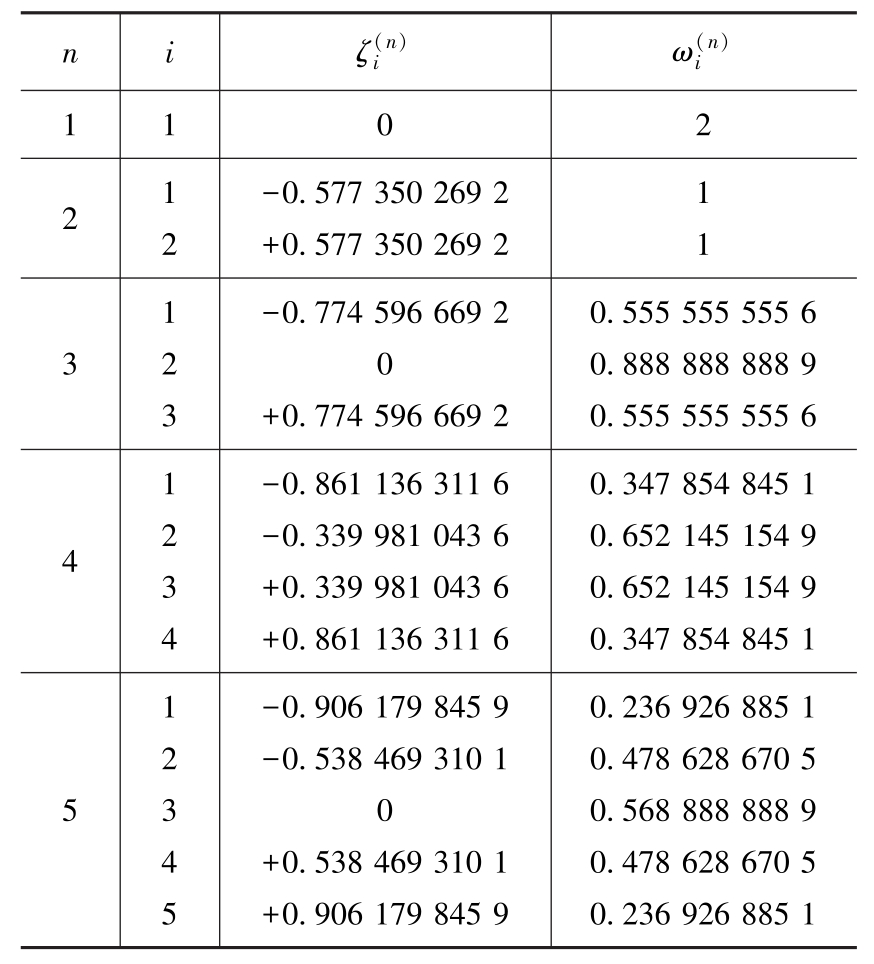
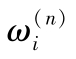 的值按表1.4-14选取(
n
最大的值参见文献[15])。
的值按表1.4-14选取(
n
最大的值参见文献[15])。
该式在区间[
a
,
b
]通过变换
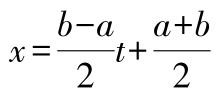 可化成区间[-1,1]上的积分:
可化成区间[-1,1]上的积分:
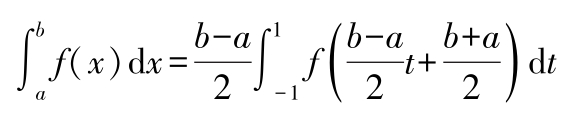
表1.4-14 一维高斯积分点的位置和权因子
(1)常微分方程的数值计算方法 对于一阶方程(边界条件为 y 0 = f ( a ), y n = f ( b ))的边值问题,主要的数值解法有尤拉公式、后退的尤拉公式、改进的尤拉公式、龙格-库塔法、阿达姆斯预测校正法等。对于一阶方程组的计算有改进尤拉法、龙格-库塔法等。高阶方程边值问题一般化为一阶方程组求解。一阶方程的四阶龙格-库塔法经典公式:
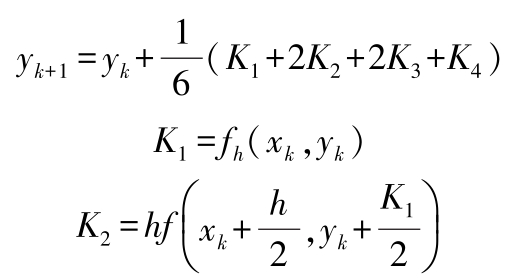
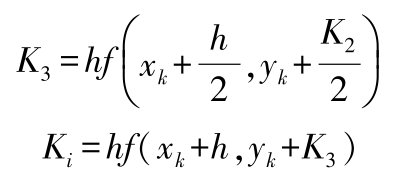
♣MATLAB中常微分方程的数值解法:ode
格式:[t,y]=ode23(‘fun’,tspan,y0)2/3阶龙格-库塔法。
[t,y]=ode45(‘fun’,tspan,y0)4/5阶龙格-库塔法。
[t,y]=odell3(‘fun′,tspan,y0)高阶微分方程数值方法。
式中 fun——定义函数的文件名,函数fun必须以dx为输出量,以t、y为输入量;
tspan[t0,tfina]——积分的起始值和终止值;
y0——初始状态列向量。
(2)偏微分方程的数值计算方法 双曲型、抛物型和椭圆型三类方程可用有限差分法和有限元法求解。1)有限差分法用差商代替偏微分方程中的偏导数,得到相应的差分方程,通过差分方程得到偏微分方程的近似解;2)有限元法将连续场域剖分成有限个基本单元,优点是对任意边界形状的求解域比差分法有更强的适应性,但不能由场的方程直接离散成代数方程组,必须按变分或伽辽金法与分片插值相结合的原理,离散后得数值解。
♣MATLAB提供了一个专门用于求解偏微分方程的工具箱——PDE Toolbox(Paticial Difference Equation)。双曲型、抛物型和椭圆型等偏微分方程都能求解,由于需要编程来实现,故不详细介绍。
(3)代数方程组的数值计算方法 线性代数方程组的直接法主要有高斯消去法、高斯-约当消去法(无回代)、克劳特分解法(LU分解法) [16] 、杜利特勒分解法、平方根法(系数矩阵正定对称)、追赶法(系数矩阵是对角占优的三对角阵)等。直接法占内存大。
线性方程组的迭代法主要有雅可比(Jaco-bi)迭代法、高斯-塞得尔迭代法、逐次超松弛迭代法(SOR法)等。迭代法只存非零元素,编程简单,但对迭代初值要求较高。
非线性代数方程组主要有牛顿-拉夫逊迭代法 [17] 。
在电磁场数值计算中,常采用预处理共轭梯度法(ICCG法),可节省大量内存(只存非零元素),系数阵与右端向量经过预处理后,系数矩阵条件数下降,收敛速度加快,CPU时间显著减少。详细做法参见参考文献[8]。