




变压器和电感在磁场中的建模问题是磁元件研究的主要问题,主要包括交流电阻、漏感、磁心损耗、寄生电容等多个方面的研究。
1855年,发明傅科摆(1851年,傅科在67m长钢丝下面挂一个重28kg的铁球,组成一个单摆,他利用摆平面的转动证实了地球有自转,演示地球有自转的这种单摆后称为傅科摆。)的法国发明家莱昂·傅科(Jean-Bernard-Léon Foucault)首次发现了涡流效应(eddy current effect)的存在,他设计了如图3-11所示的装置,包含一个可旋转的铜盘和一个磁铁产生磁场。当旋转铜盘到一定速度时松开双手,铜盘的转速随之下降,并且发热严重,由此证明了涡流效应的存在。

图3-11 傅科铜盘
➢Dowell公式
1966年,丹麦哥本哈根Telephone Fabrik Automatic公司的P.L.Dowell先生发表了“Effects of eddy currents in transformer windings” [11] ,在其中提出了被后人称为“Dowell公式”的变压器绕组交流电阻计算公式,至今仍然广受应用。
Dowell假设在典型的变压器结构中,产生绕组损耗的磁场方向为在磁心窗口中平行于绕组层的方向,即为图3-12中m.m.f箭头所示方向(m.m.f为magnetomotive force简称,也就是磁动势,即所研究环路内电流与匝数的乘积)。因此,变压器窗口中沿着一次侧与二次侧方向,磁动势随着包含的一次电流匝数增加而增加,又随着包含的二次电流匝数增加而减小,呈现出类似“小山坡”的分布,而“坡顶”即为磁动势及产生损耗最高的部分。而高频中常用的交错绕组(即三明治结构)可以有效压低“坡顶”高度,达到降低损耗的目的。可见,对绕组损耗的建模工作可以直接指导优化设计绕组结构。
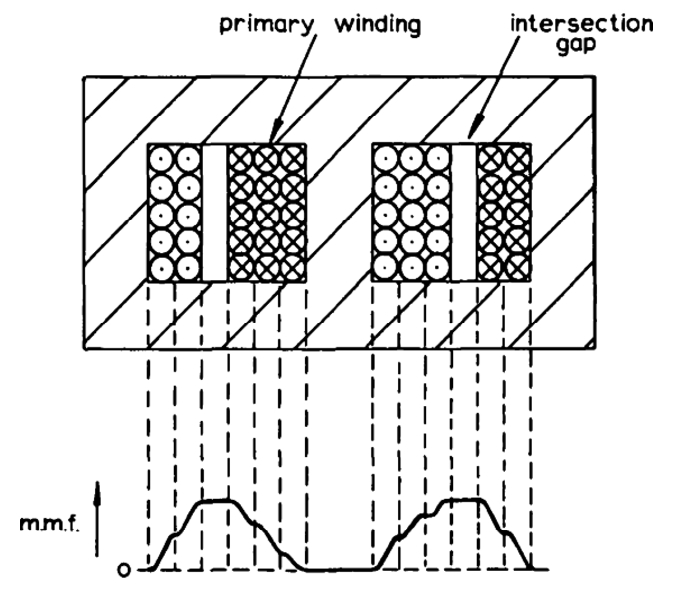
图3-12 变压器结构
在上述磁场形式假设的基础上,Dowell给出了交流绕组电阻的解析解,如图3-13所示为绕组交流电阻和直流电阻之比,即为交流绕组电阻系数 F R 。相同绕组直径下,随着频率及绕组层数的增加,电阻损耗呈现非线性急剧增长。由模型同样可以得出,在高频应用场合,减小绕组直径及层数是减小绕组损耗的有效方案。
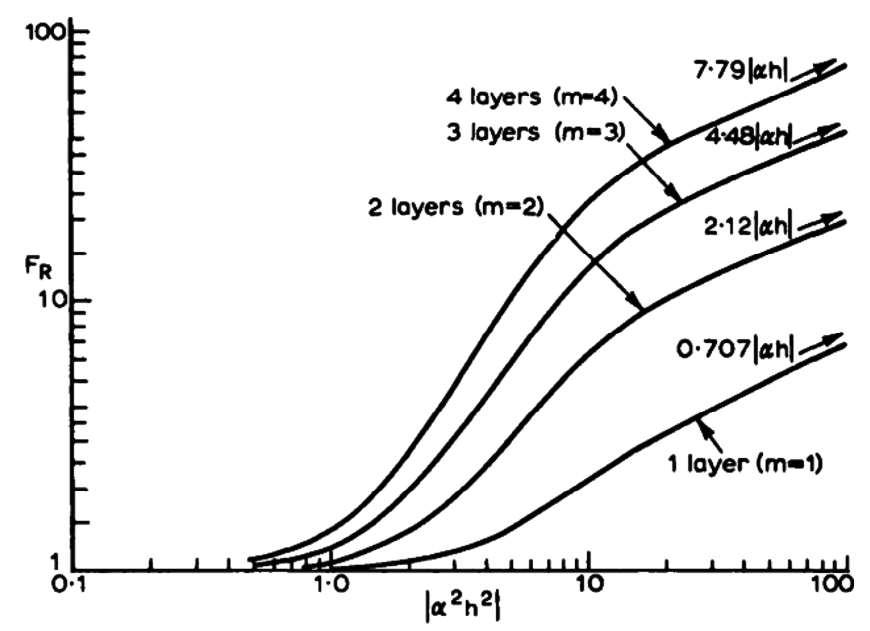
图3-13 绕组交流电阻和直流电阻之比
Dowell方法因为其形式相对简单、不受非线性磁心影响、对不同形状绕组及磁心的适用性广等诸多优点,目前仍是计算电感和变压器绕组损耗的主流方法之一,与此同时,为了克服其在不同应用背景下的适用性问题,进一步提升其计算精度,也诞生了一系列衍生及修正公式。
➢Ferreira公式
1990年,南非Rand Afrikaans University的Jan Abraham Ferreira教授提出了计算绕组损耗的另一种新思路,不同于Dowell公式的直线形磁场,其基于圆形导体的环形磁场分布推导而得,被称为“Ferreira公式” [12] 。Ferreira教授在2015—2016年期间担任IEEE电力电子学会PELS主席。
Ferreira教授的工作是在1964年学者Jiri Lammeraner和Milos štafl的总结上进行进一步拓展,后者在其著作 Eddy currents 中详细推导了单个圆导体中由于通入高频电流所产生的涡流效应磁场及其等效电阻和电抗 [13] ,其求解思路主要是依据Maxwell公式加边界条件求解磁场。值得注意的是,这本书也同时提到了单层铜箔中的涡流效应及其电阻、电抗的推导公式,其结果中使用的双曲线函数sinh、cosh等与Dowell推导的公式如出一辙。因此可以认为是这本著作中已经出现了单层铜箔的Dowell公式及单股圆导线的Ferreira公式,而后被推广应用至更一般化的应用场景。作为第一部捷克斯洛伐克关于涡流的著作, Eddy currents 这本书较为系统地综述了当时电气工程学科中涡流场问题。同时需要指出的是,真正的单股、多股导体中涡流损耗公式的最早起源恐怕已经难以考证,因为该书中也提到,早在1906年R.Rudengerg出版于德国斯图加特的 Energie der Wirbelströme in elektrischen Bremsen und Dynamomaschinen (电制动器和发电机中的涡流能量)、1917年Howe G.W.O发表于英国皇家学会学报的“The high-frequency resistance of multiply-stranded insulated wire”及1932年P.Bunet在巴黎的 Courants de Foucault (涡流)等论著中对该课题已有论述 [14] 。
Ferreira教授提出Ferreira公式的一个重要前提是他指出了趋肤效应和邻近效应的正交性(Orthogonality) [15] ,也就是可以分别求解产生两者的磁场,根据磁场求取涡流损耗再进行直接相加,即可得到绕组的总损耗。正交性原则的提出简化了绕组损耗的计算复杂程度,它不需要人们从一开始就合成趋肤效应和涡流效应磁场并进行损耗计算,且提高了人们对该问题的认知水平。进一步地,根据类似的推导方法,同样可以推导出不同频率下的磁场对绕组损耗的影响也是正交的。即对于非正弦波形下绕组的损耗,可以分别计算傅里叶分解下波形不同频率中的损耗,再对损耗进行叠加即为总损耗。这大大方便了绕组损耗的解析与分析。与之对比而言,磁场在磁心中的损耗无法进行频率范围下的叠加,这个问题就变得复杂得多。
结合单导体中的电阻建模工作及趋肤和邻近效应的正交性,Ferreira分析了圆形导体外部的磁场,并推导出了适用于圆形导体绕组的Ferreira公式。由于大部分绕线绕组均为圆形绕组,而Ferreira公式是基于圆形绕组磁场提出,因此理论上Ferreira公式相比于Dowell公式在计算圆形绕组损耗时具有更好的精度。
最后值得一提的是,尽管Dowell公式和Ferreira公式初始推导分别面向铜箔及圆导线,然而根据导体面积等效转换原则,两者分别可以进行修正用于计算圆导线和铜箔。面积等效转换原则主要是对所输入的铜箔厚度或圆导线直径进行修正,以使其等于转换后的圆导线及铜箔面积。这一原则后来被证实是没有物理及实际意义的假设,然而并不妨碍其在大部分应用场景下均能取得较好的精度。最后更精巧的是,Dowell公式和Ferreira公式在高频下可以进行互相转换和化简,已有研究证明,在忽略一些本身影响不大的展开项时,二者是相等的。因此建模的本质是数学计算,针对同一类事物数学的建模方法在此达到殊途同归的结果。
➢Dowell公式和Ferreira公式的改进
Dowell和Ferreira公式的提出为现今绕组损耗及电阻计算建模框架奠定了基础,而后发展了多种类型的绕组电阻计算方法,大致可以归类为修正的Dowell或Ferreira解析公式、半解析Dowell或Ferreira公式、有限元/有限差分仿真方法等。其中仿真的方法主要借助于仿真工具和程序,在此不做具体展开。而前两类方法主要针对其在各类情况下的推广,以及Dowell和Ferreira公式中的一维直线磁场假设及圆环磁场假设与实际磁场分布有偏差的问题。
根据造成偏差的因素总结,首先是磁心及绕组结构导致的二维效应,即磁场不仅在与铜箔平行的部分产生损耗,其在铜箔端部因为二维磁场也产生相应的损耗。1997年Soft Switching Technologies公司的Nasser H.Kutkut提出这类损耗可以通过对端部二维磁场进行建模 [16] 。
其次是由于绕组每匝之间的孔隙导致的磁场非一维分布。孔隙的产生是由于绕组本身的绝缘、绕制过程中的弯曲程度不均匀、设计时较低的窗口系数等多种因素造成,这给磁场扭曲创造了条件,造成了解析表达式的不准确。早在1990年Ferreira教授就提出可以采用孔隙率 η 修正Dowell公式,以提高其在低孔隙率情况下的精度。2002年意大利佛罗伦萨大学的Reatti和美国怀特大学的Kazimierczuk又提出可以采用孔隙率 η 修正Ferreira公式 [17] 。东南大学沈湛副研究员对这一问题也进行过研究,他认识到绕组匝与匝之间不但在同一层会有空隙造成孔隙率增大,不同层之间由于绝缘、缠绕松紧程度等原因也会产生空隙,并进一步造成绕组的移位,这将相应造成磁场的扭曲分布,客观上拉长了磁场的轨迹,削弱了磁场强度并造成等效电阻的降低,如图3-14所示,针对此现象他引入了相关结构参数进行了磁场及电阻的修正工作 [18] 。
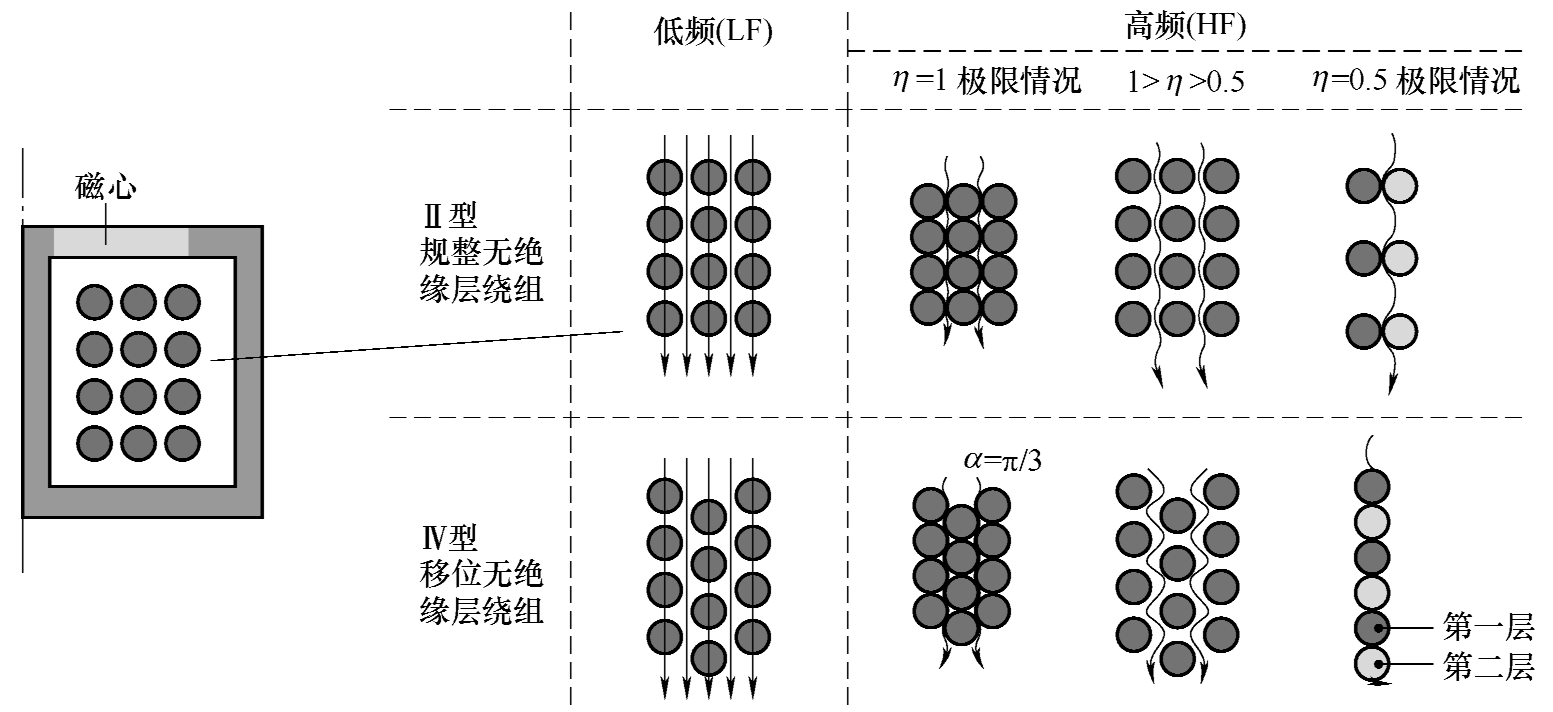
图3-14 绕组的孔隙率及移位分布
最后是磁心气隙、形状等其他结构造成的磁场的扭曲分布。针对该类问题的解决有2014年瑞士苏黎世联邦理工大学Jurgen Biela教授提出的半数值公式方法 [19] 、2001年德国ASCOM Energy Systems GmbH公司P.Wallmeier提出的纯解析方法(其表达形式相当复杂,公式满满一页A4纸) [20] 、2012年福州大学陈为教授等提出的镜像法 [21] 、2022年Jurgen Biela教授提出的泊松方程直接解磁势法 [22] 等。
➢利兹线损耗模型
利兹线(Litz wire)起源于德语单词Litzendraht,意思是“编织线”。它是由多股导线绞绕及编制缠绕而成,旨在减小高频下绕组的等效电阻。利兹线在20世纪上半叶主要应用于无线电广播、射频系统、超短波扼流圈等通信领域器材,随着新型元器件技术的快速发展及电力电子技术的进步,利兹线越来越多地被应用于高频下的功率变换领域。在高频下,传统实心导线由于趋肤效应的影响,电流趋向于向导线的表面分布,这会导致导体芯部流经较小的电流甚至不流通电流,导线实际有效流通面积急剧减小,等效电阻急剧增大,发热及损耗严重。这一现象随着频率的增大而逐步恶化。而利兹线的使用可以在一定频率范围内有效地削弱这一效应的影响。
利兹线的制作是将多股漆包线按照不同的方式进行绞绕拧合成整体,如图3-15所示 [23] 。较细的漆包线的使用使得高频下的趋肤效应不显著,所有漆包线都能有效导通电流,利用率高,而多股漆包线的组合应用保证了利兹线的总导通面积,因此可以流经较大的高频电流。值得注意的是,使单股漆包线能均匀导电必须要求利兹线在制作过程中采用股与股之间的有效绝缘以及频繁的交叉换位。股与股之间的绝缘保证了其每股之间电流互不干扰,否则整根导线在磁场中将被等效为单股大直径实心导线,即位于中心的导线依然不导通电流;频繁的交叉换位保证了每股漆包线在物理位置上地位相似,即获得相似的内部及外部磁场的影响,保证了每股漆包线中电流及损耗也接近。

图3-15 不同类型的利兹线举例
利兹线脱胎于传统圆导线,然而又有较为复杂的结构,导致其在损耗计算方面与传统漆包线既有联系又有区别。美国达特茅斯学院Charles R.Sullivan教授在利兹线建模方面有较为深入的研究。他于1999年提出利兹线所受的磁场可以区分为股级效应(strand-level effect)和束级效应(bundle-level effect),如图3-16所示 [24] 。同时结合导线中各类涡流效应之间的正交特性,可以分别计算图中的各类效应产生的等效损耗和等效电阻,再将其相加即可得到利兹线总电阻。
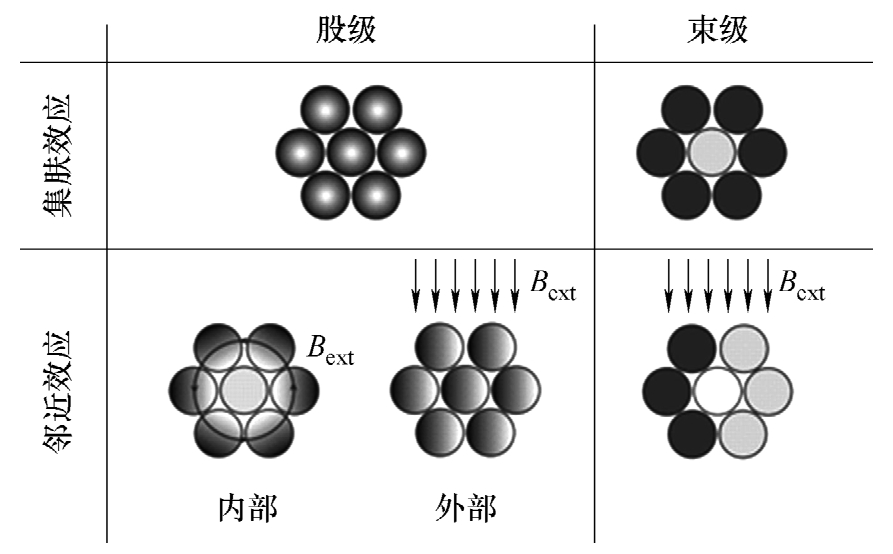
图3-16 利兹线的股级和束级涡流效应
关于非理想Litz线线圈电流均衡问题,瑞士苏黎世联邦理工大学的Kolar教授和武汉大学邓其军教授对此都有较为系统的研究。
最后,已有诸多文献证明,利兹线的适用范围大约在10kHz~5MHz之间,如图3-17所示 [25] ,为圆导线和利兹线交流电阻率对比,其中交流电阻率=交流电阻/直流电阻。也就是说,若两种导线的直流电阻即导通截面积相等,则该例子中在一段区间内利兹线损耗占优,在更高的频率范围外利兹线损耗急剧增加,反而比圆导线损耗还大。这是因为利兹线的等效层数比圆导线大得多,随着频率的增加层数带来损耗急剧增加而导致。所以,通常利兹线适用于若干MHz以下的应用场景。而针对MHz以上的场合,空心圆导线或者细铜箔目前更为适合,例如美国麻省理工学院研制的基于水冷空心圆导线的高频大功率电感 [26] 。
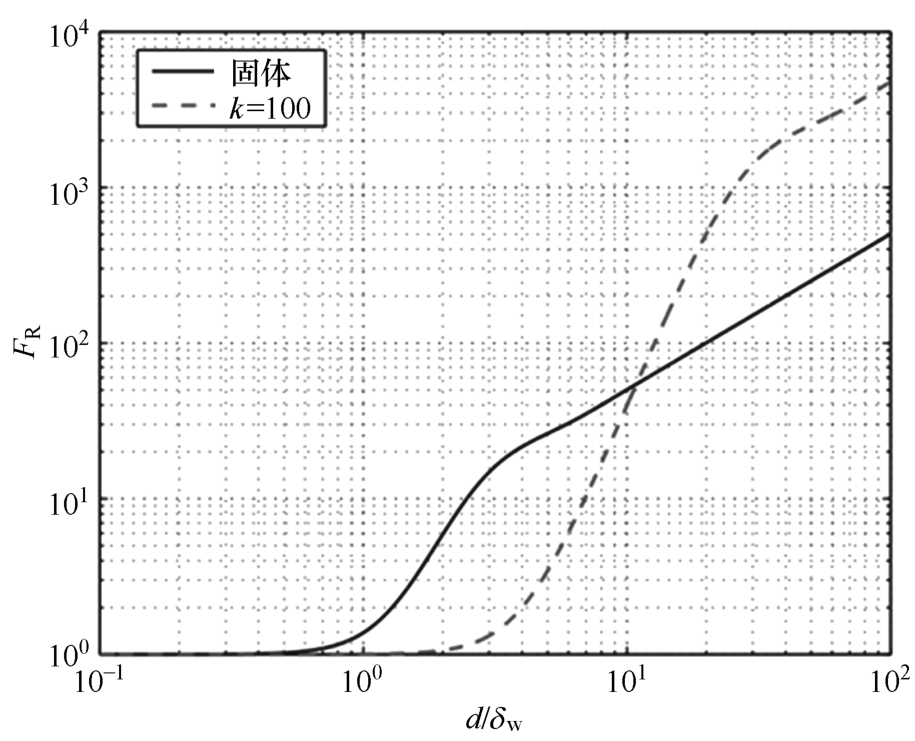
图3-17 圆导线和利兹线交流电阻率对比
➢和频率无关的模型
变压器漏感建模中,和频率无关的模型建模比较简单,具体提出时间已难考证。根据图3-18所提供的正常/交错绕组的磁动势图,可以很简单推导出不考虑频率影响情况下,漏磁场所积累的漏磁能量,从而计算出变压器的漏感。如W.G.Hurley教授等所著 Transformers and inductors for power electronics 中的第6章、Vencislav Cekov Valchev教授等所著 Inductors and transformers for power electronics 中的第9章、南京航空航天大学赵修科教授所著《开关电源中磁性元器件》中的第6章等。该模型简单易用,所依赖的参数较少,在工频或者精度要求不高的高频场合有广泛的应用。
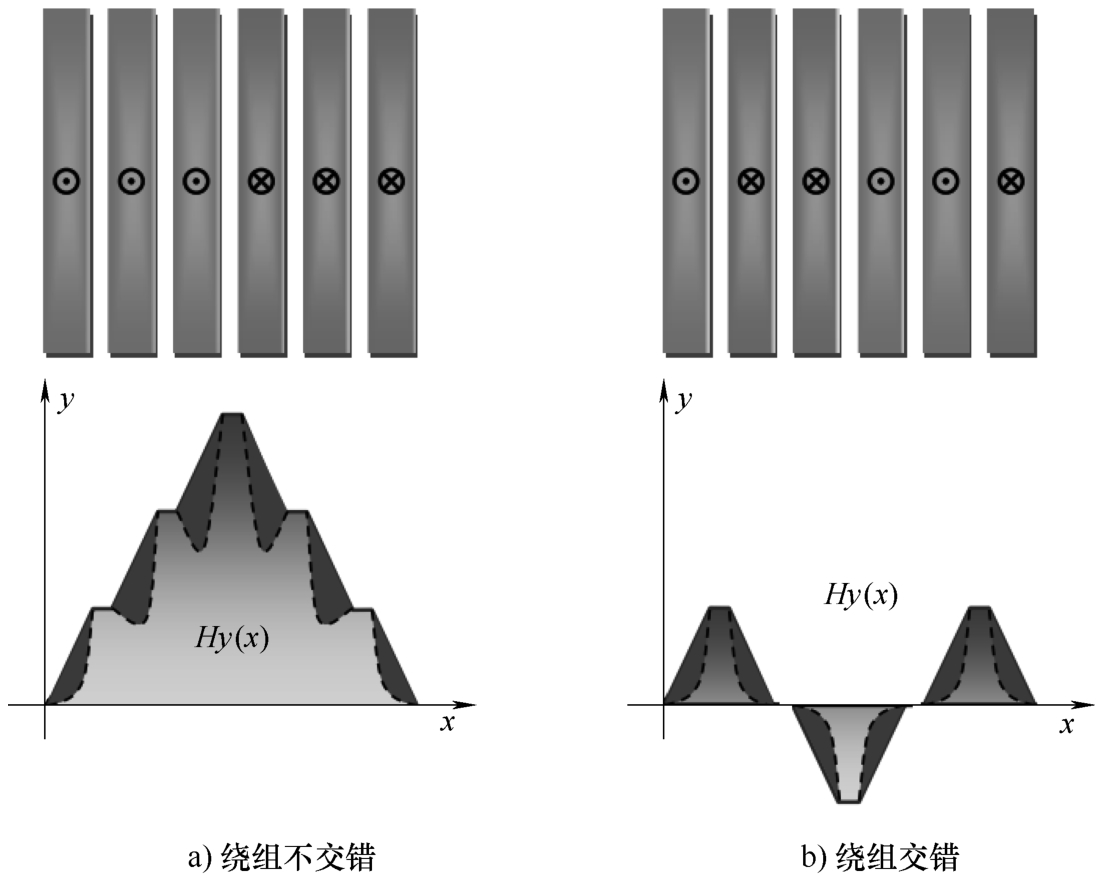
图3-18 产生变压器漏感的电磁场
➢和频率相关的模型
若考虑频率的影响,则还需要考虑导体内部的涡流效应对漏感的影响。事实上,Dowell在其1966年的论著中不仅谈到了计算电阻的公式,还同步给出了计算常规变压器漏感的Dowell漏感公式 [11] 。这是由于变压器内部的短路漏磁场既会在绕组内部产生阻性涡流损耗,被等效为交流电阻效应,漏磁场本身又会在绕组内部、绝缘层、空气层等存储漏磁能量,被等效为漏电感效应。Dowell通过计算漏磁场等效的阻抗,分离出实部即为交流电阻,分离出的虚部即为漏感。和交流电阻相反的是,漏感随着频率增加而下降,这是因为随着频率的提升,趋肤效应增强,磁场在导体中分布的区域减小,造成磁场能量相应降低的缘故。
类似电阻公式,在更早于Dowell推导出漏感公式以前,业界也已对单股或多股导线中的阻抗进行过解析推导,例如1964年的Lammeraner和štafl推导的圆导线的高频电感阻抗 [13] 等。而后,一系列漏感计算公式进一步被提出。1994年爱尔兰国立大学的William Gerard Hurley教授基于Maxwell公式推导了环形磁心构成变压器的漏感,并进行了适当简化 [27] 。2015年瑞典查尔姆斯理工大学的Torbjorn Thiringer教授提出了一种更加精细化计算绕组漏感的公式,其对绕组内部每层间绝缘、每匝绝缘、每匝导体等部分均做了精细化磁场建模工作 [28] 。2016年法国里尔中央学院的谭文华博士提出直接求解泊松方程,采用多层格林函数求解平面变压器的漏感 [29] ,2019年美国田纳西大学Fred Wang课题组运用数据挖掘算法计算漏感,为漏感建模提供了新思路 [30] 。本书作者所在课题组在利兹线绕组漏感精确建模方面也有相关工作 [31] 。
1892年,美国GE公司的斯坦梅茨(其事迹见第1章)在美国电气工程师协会发表了关于磁滞损耗的论文,提出了后来被称为“Steinmetz公式”的计算方法 [32] :

其中, P s 是每单位体积的时间平均功率损耗, f 是频率, B m 是峰值磁通密度; K 、 a 和 b 称为Steinmetz系数,通常通过对不同材料磁心损耗的测量并拟合上述公式,从而获取其对应的Steinmetz系数。
尽管Steinmetz公式的系数主要通过测量和拟合获得,然而由于其通用性广、结构简单、所需参数少、精度好等诸多特性,至今仍被广泛应用。值得一提的是,Steinmetz之后还提出在交流电路稳态和瞬态分析中引入复数理论,凭借此项贡献被认为是“教会了整整一代工程师如何处理交流现象”。
Steinmetz公式本质上属于经验公式,且原始的Steinmetz公式仅适用于正弦波形,随着电机、电力电子等的广泛应用,磁材料需要工作于方波、梯形波等非正弦电压工况。而与绕组损耗不同的是,磁心损耗计算无法对波形进行傅里叶分解后分别计算各个频率损耗再进行叠加,因此原始的Steinmetz公式应用范围受限。基于非正弦下磁心损耗的计算问题,也有诸位专家进行了改进。
2001年德国亚琛工业大学Rik W.De Doncker教授课题组提出了修正的Steinmetz公式(modified Steinmetz equation,MSE) [33] ,认为磁心损耗和宏观磁化率d M /d t 相关,而后者和磁感应强度变化率d B /d t 又直接相关。基于这一物理原理解释,课题组提出了周期非正弦波形的平均频率 f eq 的概念,将平均频率这一概念代入原始Steinmetz公式可以计算出周期非正弦波形的损耗。这一方法不足之处在于并非所有波形都可以用平均频率计算。
2001年美国达特茅斯学院Sullivan教授提出了generalized steinmetz equation(GSE)方法 [34] ,课题组提出了磁心瞬时功率损耗仅和瞬时磁密 B 和磁密变化率d B /d t 相关这一假设,因此直接提出了关于周期 T 、 B 、d B /d t 以及Steinmetz系数的公式,然而,后续研究论证了这一假设存在问题,即损耗不仅取决于 B 和d B /d t ,而是取决于这个周期的所有信息,因此GSE公式精度并不理想。基于上述尝试和发现,Sullivan教授课题组于2002年又提出了improved generalized Steinmetz equation(IGSE),大大改进了GSE并被沿用至今 [35] 。河北工业大学辛振教授课题组对由Steinmetz公式引申出的一系列方法总结如图3-19所示 [36] 。
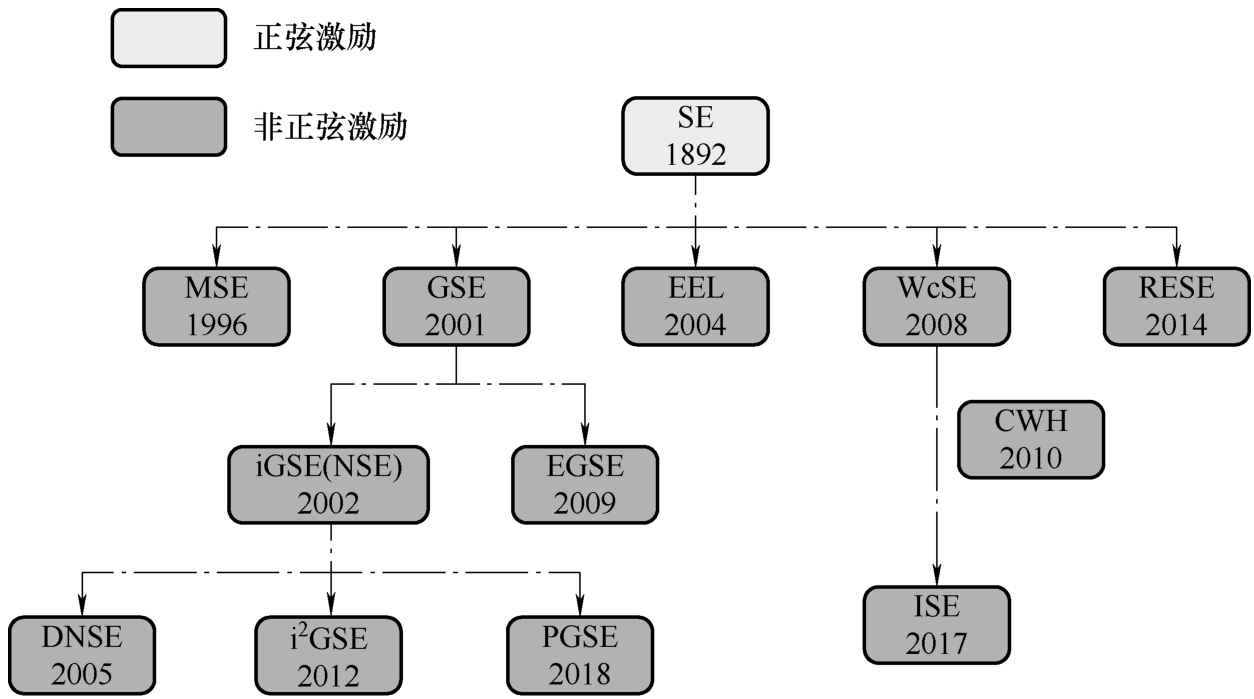
图3-19 Steinmetz公式及其改进
除了Steinmetz公式系列之外,其他损耗计算方法主要包括损耗分离法、磁滞模型法以及查表法等等。传统损耗分离法将磁心损耗分离为磁滞损耗及涡流损耗,而1986年Bertotti认为磁心中还存在第三种损耗,即“异常损耗”(anomalous loss),这项损耗是由畴壁运动的结果。由于磁心损耗建模方法的高度非线性和复杂性,目前也有提出采用先进算法的分析手段,例如美国普林斯顿大学陈敏杰教授发起的MagNet Challenge 2023挑战,主旨为采用人工智能及大数据方法计算复杂波形下磁心损耗。
近年来,随着宽禁带器件的逐步推广应用,磁元件的分布电容问题引起了业界越来越多的重视。而分布电容问题早在20世纪初期就已经被注意,主要在无线通信领域中线圈的制作和测量。1902年P.Drude在发表设计特斯拉变压器的论文时,认识到线圈存在着等效电感及等效电容 [37] 。同时他采用谐振法测量到了等效电容,他将测量到的线圈固有电容值加上特斯拉变压器外加电容形成总电容,所得特斯拉变压器谐振频率误差小于1%,论证了电容测量方法的准确性。1915年,Thompson等人发表了由于变压器寄生电容存在导致的过电压问题的论文 [38] 。
➢单层绕组电容
1912年W.Lenz通过理论计算获得了单层线圈的总电荷,并建立了考虑每匝线圈电位分布的电容网络结构,如图3-20所示 [39] 。1921年G.Breit发表了一系列计算分布电容的论文 [40] ,他将线圈等效成无数的与轴向垂直的小段,并忽略线圈电阻,他从磁场角度计算,并给出了从电感量出发采用积分计算分布电容的思路。1936年,A.J.Palermo指出,前人的工作没有考虑线圈粗细或者匝间距离等影响,因此导致了种种误差,并给出考虑这些影响的简便公式 [41] 。
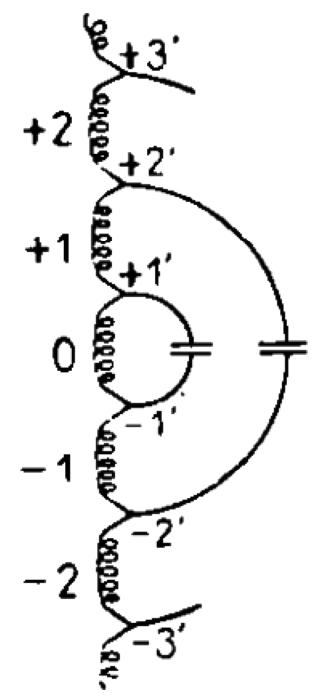
图3-20 W.Lenz提出的线圈等效图
尽管对于线圈电容的测量方法早有共识,但是早期学者对于单层线圈电容的理论解析计算方法与思路各异,其结果往往要么是较为复杂的积分公式而应用受限,要么过于简化,推导假设中忽略了重要的影响条件,因此其通用性及易用性受到影响。
➢多层绕组电容
上述总结主要针对单层线圈,对于多层线圈,层与层之间也存在分布电容,且常远大于层内电容。由于线圈截面本身为圆形,若采用经典的平板电容器公式,则需要引入面积修正系数,修正计算两层线圈之间的等效正对面积,将圆形导线的正对面积转换为平板正对面积,为此,有学者提出了多种修正的等效截面积计算方法 [42-43] ,可以根据绕组的尺寸及每匝之间距离估算两层绕组、绕组和磁心/屏蔽层的等效正对面积。1968年J.Koch提出不经由平板电容公式直接计算两层线圈之间等效电容公式,并可被推广至非理想的移位绕组情况 [44] 。此外,仅计算正对面积下的电容还是不够的,因为经典的平板电容公式考虑的是两层板之间均匀电场的情况,即两层板各自板内电压恒定,板间电场强度恒定;而两层绕组中每层绕组上的电压分布也不同,而是可以看成是线性变化,这将导致层间电场不再恒定,因此等效电容降低,还需要再引入电势修正系数,进一步修正平板电容。1946年W.T.Duerdoth较为系统地计算了各种绕组连接和组构下的电势修正系数,如图3-21所示,并将其推广到任意绕组电势分布情况 [45] 。特别需要指出的是,针对我们最常使用的Z字形绕组绕制方法,其电势修正系数为1/3,即等效电容为层间平板电容公式计算结果的1/3。最后,W.T.Duerdoth还推导了分段绕组及含屏蔽层绕组的电容计算方法,如图3-22所示。
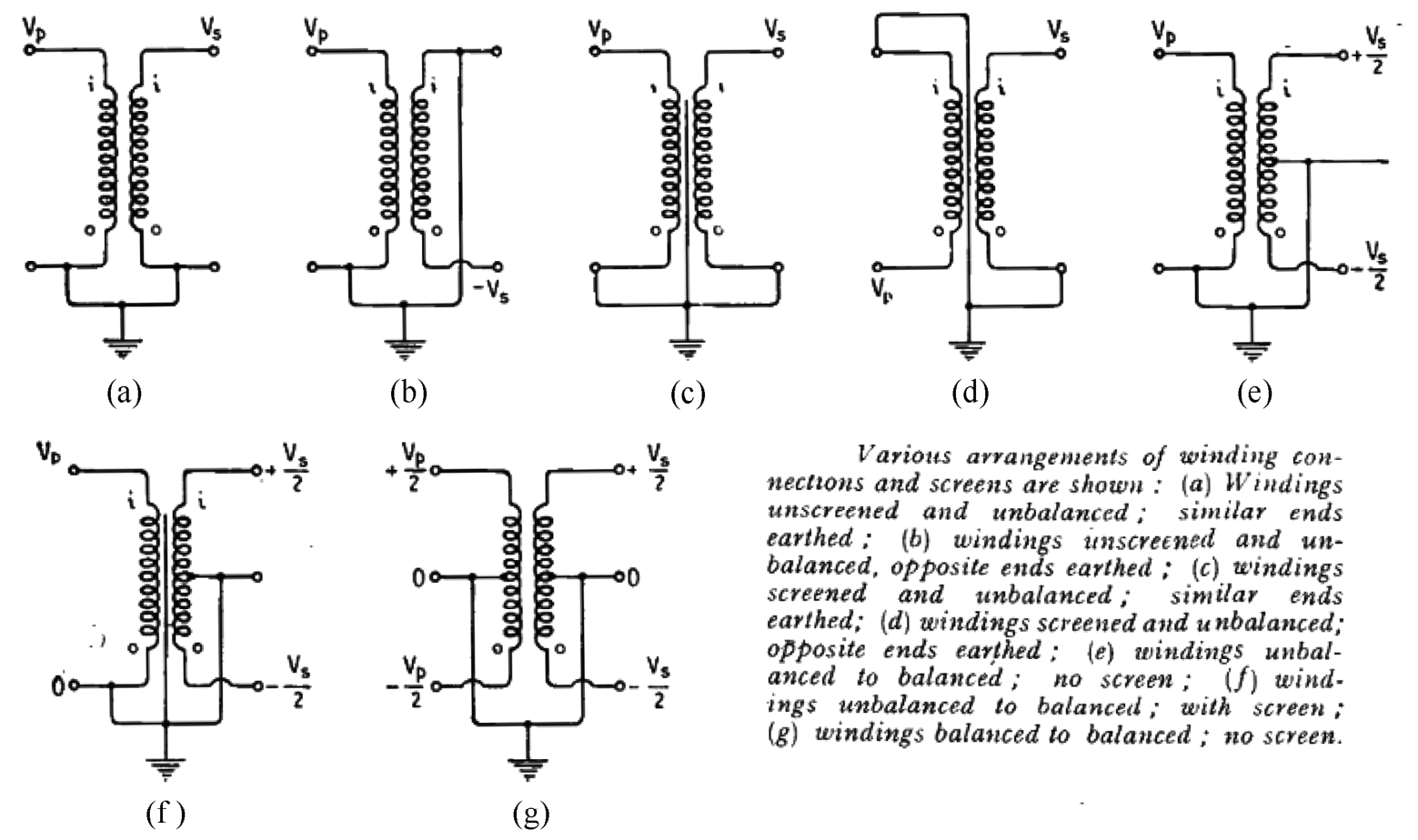
图3-21 W.T.Duerdoth计算的各种绕组连接下的电势修正系数
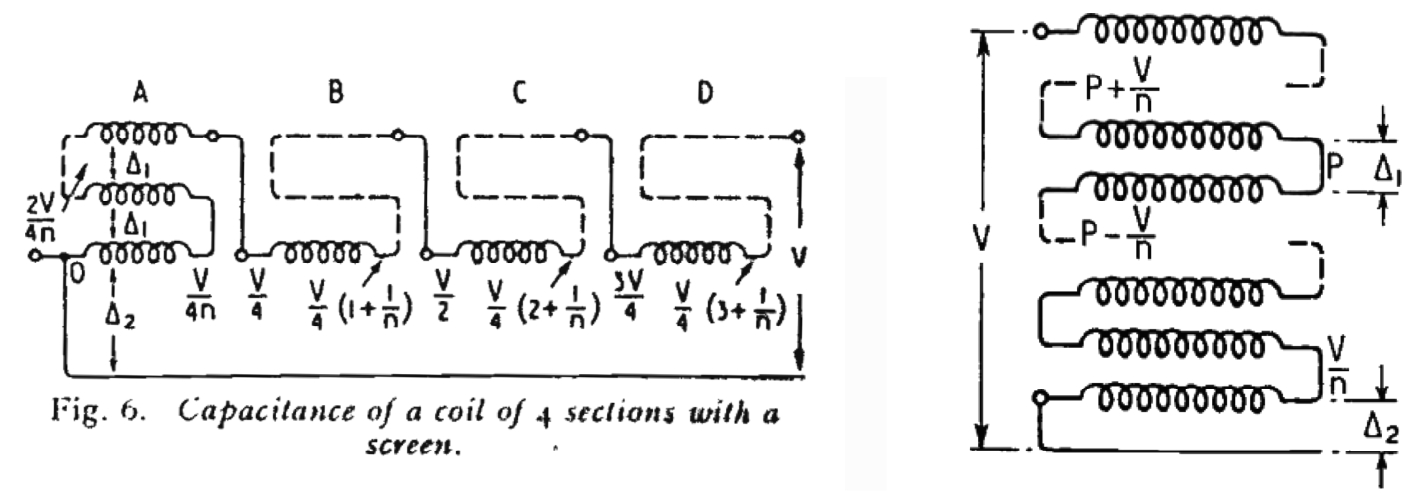
图3-22 W.T.Duerdoth计算的分段绕组及含屏蔽层绕组的电容
➢多绕组电容
变压器包含一、二次绕组,是典型的多绕组结构。1994年法国学者Bruno Cogitore等指出变压器的分布参数网络如图3-23a所示,包含了四个分布电容,随后将其简化为更为经典的三电容模型,如图3-23b所示,这一模型较好地解释了一次,二次,一、二次绕组内部及之间的电容,通用性、简便性较好 [46] 。1999年,丹麦奥尔堡大学L.Oestergaard博士提出了经典的六电容模型 [47] ,指出变压器四个端口之间六个关系都存在分布电容,进一步提升了模型的精确性,如图3-23c所示。华北电力大学崔翔教授、齐磊教授团队将其进一步发展,增加了绕组与磁心之间的电容耦合并提出了十电容模型,如图3-23d所示,可以更准确描述变压器的高频特性 [48] 。
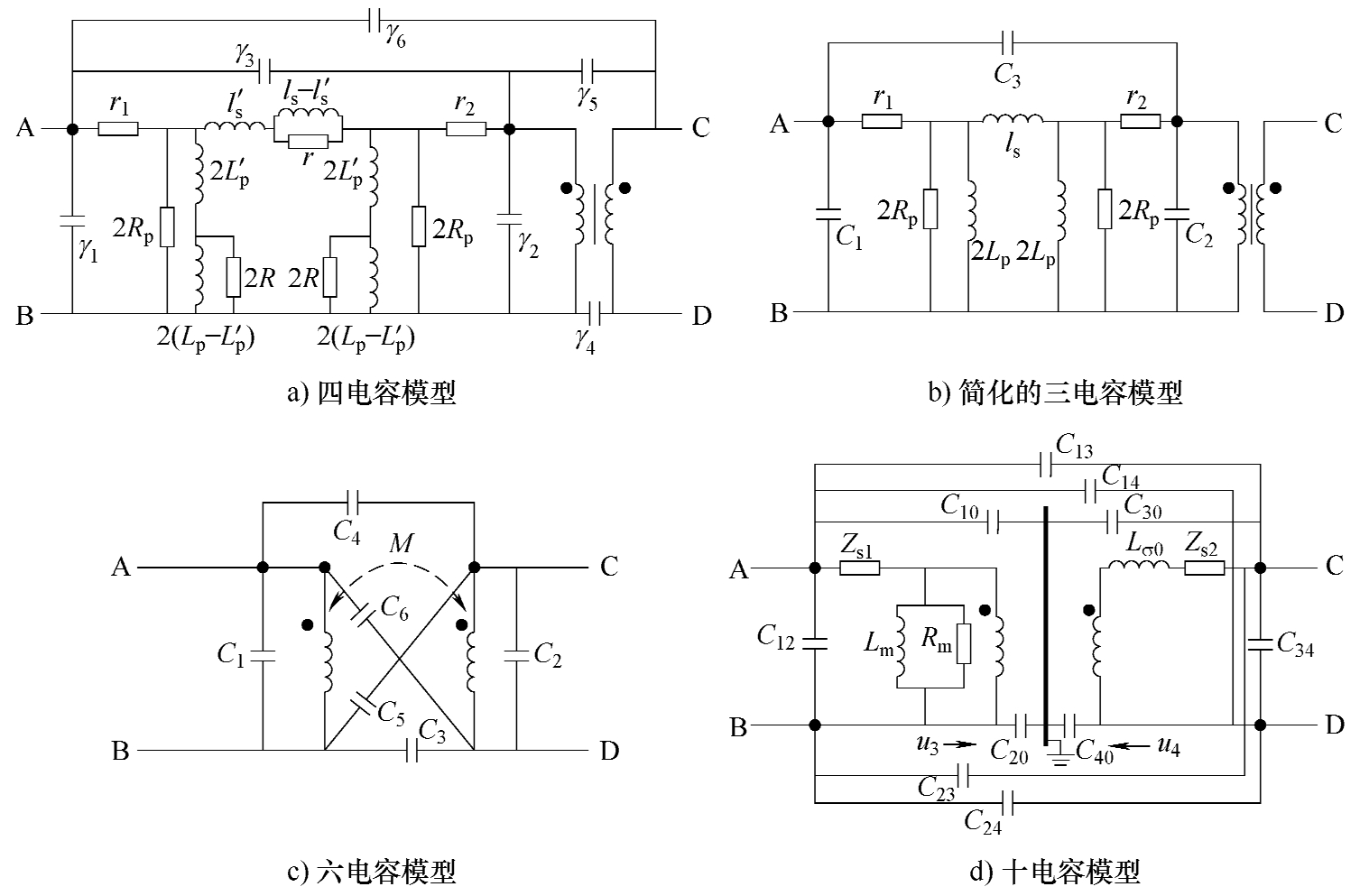
图3-23 变压器寄生电容的几种模型
随着谐振变换器、宽禁带半导体等的不断推广,磁元件的分布电容研究不断进步。美国怀特州立大学的M.K.Kazimierczuk针对线圈电容、线圈及屏蔽层之间电容、环形磁心绕制电感的电容等多种电容进行了一系列研究 [49] 。加拿大英属哥伦比亚大学M.Ordonez教授对提出了平面变压器的电容建模及优化方法 [50] ;东南大学沈湛副研究员针对绕组和磁心/屏蔽层之间电容、磁心内部电场电容等进行了研究 [51-52] ;丹麦奥尔堡大学赵泓博博士对电感中的电容有系列研究,并将现有电容建模方法总结为基于物理场的建模方法和基于外特性规律的建模方法 [53] 。瑞士苏黎世理工大学Juergen Biela和Johann W.Kolar教授对各种分布电容计算进行了系统的综述 [54] ,是入门该课题的必读文献。