第四节
圆形分布

一、概念与特点

圆形分布（circular distribution）是一种特殊的连续型分布，用于描述以方向、位置、周期性时间、角度等为测度单位的数字特征规律的统计方法。圆形分布中最常用的圆形正态分布，是由Von Mises于1918年提出的。

圆形分布资料，常见的有：昼时性资料、角度资料、季节性资料、方向性资料、圆周上位置资料、定时测定资料等。

圆形分布资料的数据可化成角度（圆心角），具有周而复始（360°即0°）、起始点及递增方向人为设定等特点。

圆形分布的数字特征，常有平均角（mean angle）、极距、角离差（angular deviation）等。

平均角，也称角均数，用于描述圆形分布资料集中于某个角度或方向、时间中发生的倾向。 n 个以角度表示的数据 α _i （ i =1，2，…， n ）， f _i 为分组频率，定义横、纵坐标均数为：

平均角 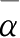可以计算为：

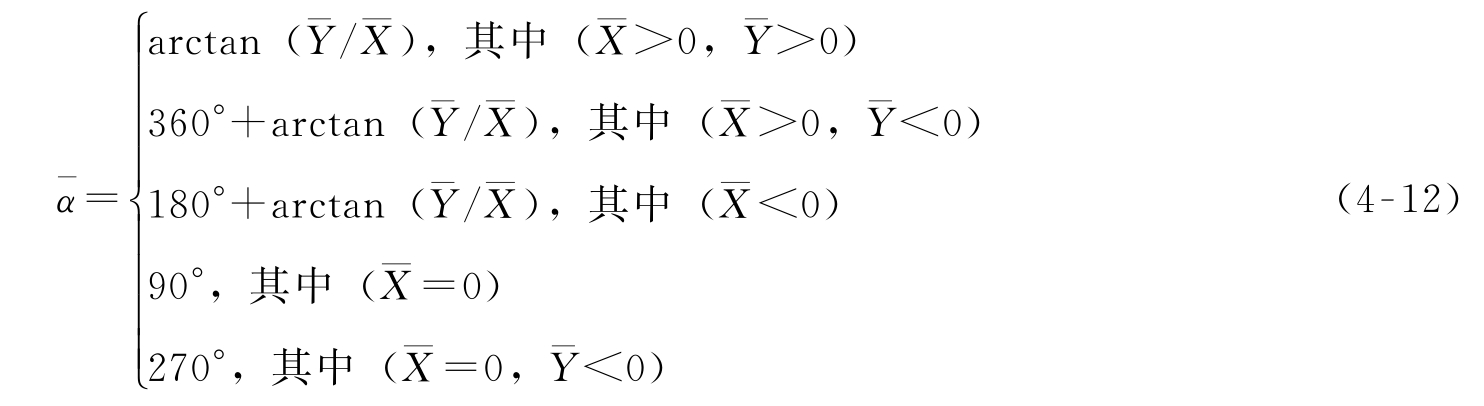
极距（平均向量长度），表示圆形分布资料的集中性，极距 r 公式为：

角离差是平均角离差的简称，也称角标准差或圆标准差，表示圆形分布资料的离散性。角离差 S 及分组校正 S _C 公式为：

r _C 为分组校正极距，具体计算公式参见式4-19。

二、应用

圆形分布的应用条件是资料呈单峰分布，角度数据要准确到度，昼夜时间要准确到时、分。昼夜时间与角度的换算，1小时换为15°、1分钟换为0.25°，即

【例4-6】 20名足月妊娠妇女的分娩时间如表4-1所示，计算平均分娩时间及标准差。

解： 这是单组昼夜时间资料。把分娩时间换成角度，计算每一角度的正弦值、余弦值，如表4-2所示。

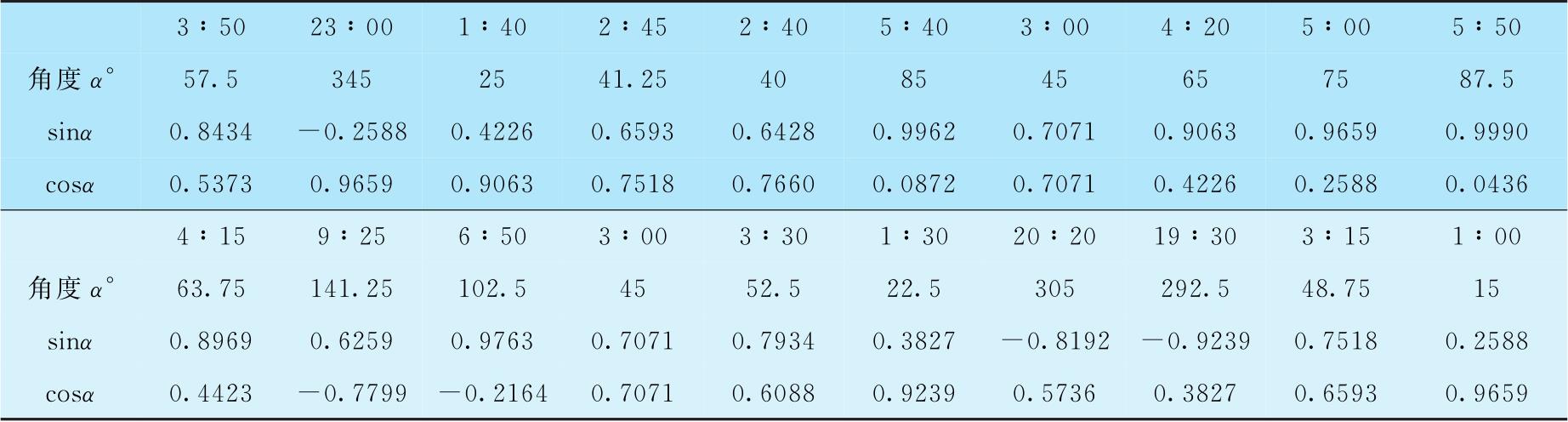
计算得到：

换为时间，得到：

平均分娩时间 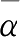=3小时9分钟，标准差 S =3小时7分钟。

圆形分布的季节资料，要准确到月、日。1～12月份，分别计为31、28、31、30、31、30、31、31、30、31、30、31天。1年365天按360°计算，以元旦零时为起点，1天相当于：

频数资料为分组资料，季节为12组、昼夜为24组。大样本时，分组校正极距 r _C 公式为：

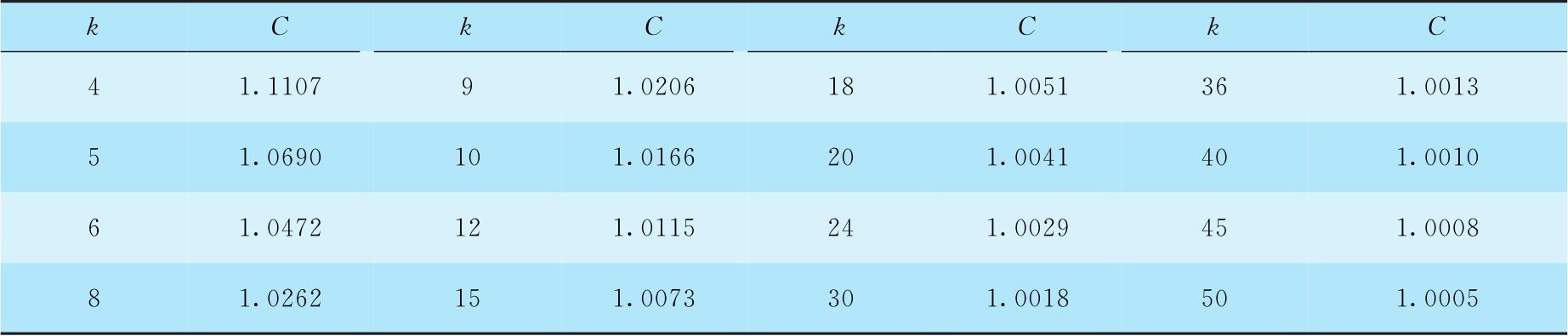
其中， C 为极距校正因子，其值可以根据组数 k 查表4-3得到。

【例4-7】 曲阜市疾病症监测点1994～1998年累计监测农村人口634950人，意外死亡529人，死亡月份分布如表4-4所示。计算5年的平均死亡时间及标准差。

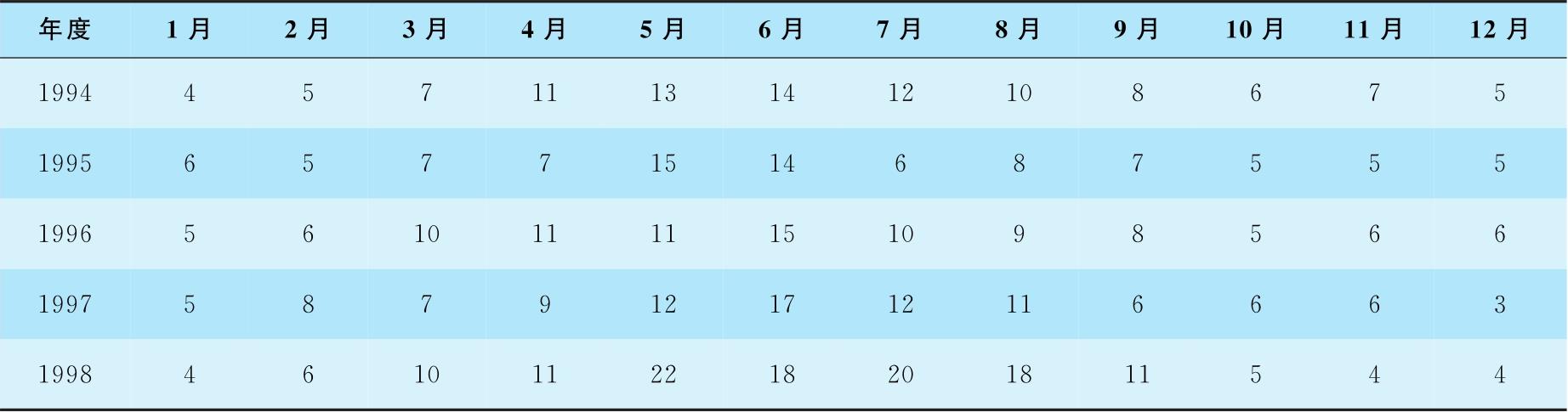
解： 这是多组季节资料。以元旦零时为起点，求各月份的组中值，填入表4-5的①列。如：1月份31天，月中点距0为15.5；2月份28天，月中点距0为31+14=45天。

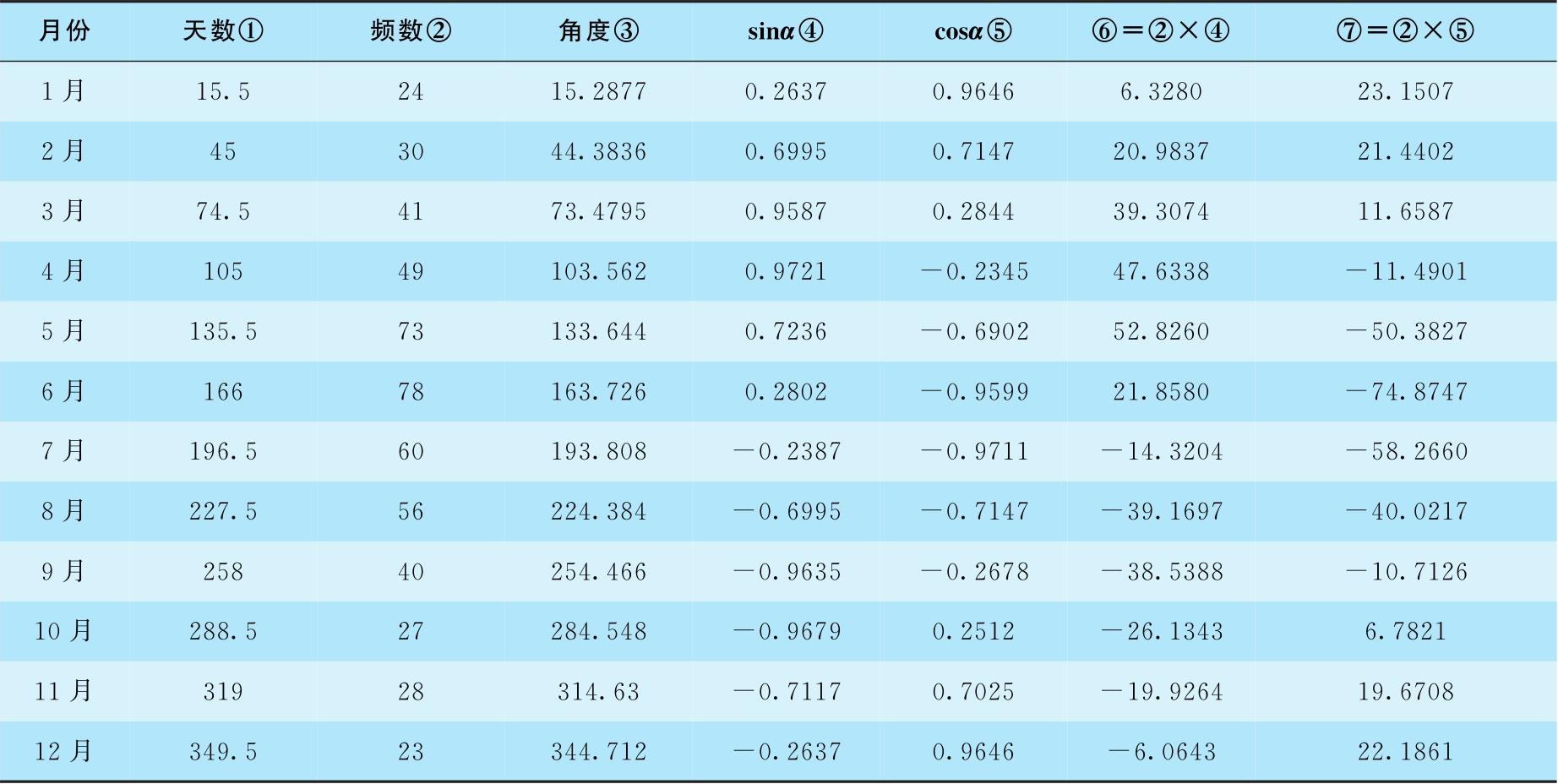
计算5年每月的意外死亡合计人数，填入表4-5的②列。将月中值折算成角度，填入表4-5的③列。一年365天，如，1月中点为15.5×360°/365=15.2877°。

求出每个角度的正弦、余弦值，填入表4-5的④、⑤列。按⑥=②×④及⑦=②×⑤计算，求②、⑥、⑦列的和得到：

查表4-3，组数 k =12时，极距校正因子 C =1.0115，得到校正极距：

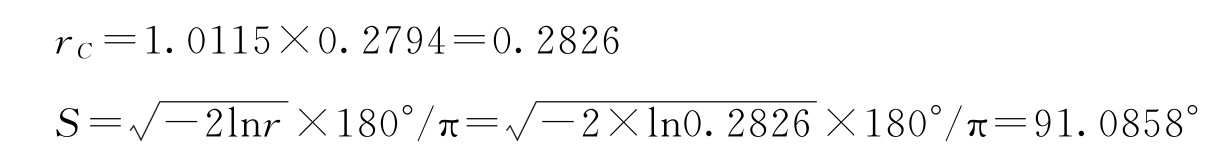
换为时间，得到：

平均死亡时间 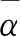=6个月14天，标准差 S =92.3509天。

思考题

1.在100支针剂中有10支次品，任取5支，计算全是次品的概率以及有2支次品的概率。

2.某种疾病自然痊愈率为0.3，现有20个患者服用一种新药，若其中半数以上人痊愈，试说明可否认为这种药有效？

3.若200mL当归浸泡液含某种颗粒300个，分别计算1mL浸液含2个、超过2个颗粒的概率。 4DioH299e7tz83rs6+twwAjhAztP4rXI53HcL/49Shl0f8Td0u9J0lrbWG6S4D/W