




1939年的初夏,加州理工学院校园里艳阳高照,繁花似锦。教学楼前面如茵的草坪刚刚被修剪过,散发出一股股田园青草的清香。几只喜鹊叽叽喳喳地欢叫着,尽情地在花坛和树丛中蹦蹦跳跳。
钱学森的心情像夏天一样晴朗和火热。经过3年苦读,他获得了航空和数学博士学位,成为该校当年32个博士学位得主之一。6月9日,风和日丽,加州理工学院的毕业典礼在蓝天下的草坪举行。踏着学校乐队演奏的进行曲节拍,身披黑袍的钱学森与同为新科博士的同学们一起戴上了博士帽。
钱学森具有学术奠基意义的博士论文,是他于1938年完成的《可压缩流体运动和反作用推进问题》,论文包括四个部分:
第一部分《可压缩流体边界层》(Boundary Layer in Compressible Fluids),1938年1月26日在第六届国际航空协会年会上发表,1938年2月发表于《航空科学学报》卷5;
第二部分《倾斜旋转体的超声速绕流》(Supersonic Flow Over an Inclined Body of Revolution),1938年10月发表于《航空科学学报》卷6;
第三部分《可压缩流体的二维亚声速流动》(Two-Dimensional Subsonic Flow of Compressible Fluids),1939年发表于《航空科学学报》卷6;
第四部分《以逐次脉冲推进的探空火箭飞行分析》(Flight Analysis of a Sounding Rocket with Special Reference to Propulsion by Successive Impulses),1939年发表于《航空科学学报》卷6。
这些论文充分显示了钱学森在科学研究方面杰出的天赋和才华,其中他与导师共同完成的《可压缩流体的二维亚声速流动》建立了闻名世界的“卡门-钱近似”公式,以其独到的见解和原创性的贡献,使他在28岁时就成了世界知名的空气动力学家,也使现代世界科技史记下了为数不多的中国人的名字。
直到今天,人们在重读这些论文时,仍然能够透过历史的尘封,看到大师的思想燧火与智慧之光。
钱学森博士论文的第一部分《可压缩流体边界层》是关于飞机在高空高速飞行时,它所受到的阻力和表面的热效应问题,也就是后来人们通常所说的“热障”问题,这是一项重大的理论突破。
当时,飞机的设计者普遍认为,飞机在超声速飞行时,空气的阻力主要是激波阻力,而表面摩擦力并不重要,可以忽略不计,而且因飞机处在高空,它的表面只会被周围的空气冷却而不会发热。钱学森从物理的角度重新对飞机结构进行了整体思考,在冯·卡门的指导下,运用了极其复杂的数学计算和逐次迭代的近似解法,求证了飞行器在高速飞行时的摩擦阻力与气动加热,以及在不同马赫数时与飞行器壁面温度的相互关系,得到了精确的数据。据此,他揭示了两条重要结论:第一,在高速飞行中,可压缩性流体对飞行体表面摩擦具有重要影响,高速飞行体因摩擦引起的阻力将超过激波引起的阻力;第二,当飞行速度达到并超过声速时,飞行体表面的空气薄层中所产生的热不仅不能被忽略,而且将对飞行体起加热作用。
在世界航空工业还比较落后的20世纪三四十年代,钱学森研究的这一全新理论,以数学的严谨和逻辑的严密,科学地预见了实现高速飞行必将面临的一大障碍,即“热障”。因此,人类在设计高速飞行的飞机时,必须对飞机表面采取有效的防热或冷却的措施。这已经成为现代气动力学的经典理论。
这篇论文虽只有薄薄的6页,但是在动笔写作前,钱学森系统地收集并阅读了海量的参考文献,仅阅读笔记就写了450多页,从中发现和改正了前人的缺点和不足,然后才开始写论文。他从基本方程出发,做了不计其数的演算来寻求答案,仅保存下来的演算手稿就有250页之多。
钱学森博士论文的第二部分《倾斜旋转体的超声速绕流》,其内容是研究火箭或导弹这类细长飞行物体在以超声速飞行时所受到的空气动力,如飞行器的升力、阻力和表面上的压力分布等。旋转体也称轴对称物体,如圆柱、圆锥、钝头锥或它们的轴向组合体。倾斜的绕流的意思是气流方向与飞行物体对称轴的方向不是平行的,而是有一定的夹角,这个夹角在空气动力学上被称为“攻角”。当时人们都关注像飞机这样的非旋转体,而在火箭、导弹实际应用初现端倪的年代,对旋转体的绕流研究是很超前的,因此该研究受到国际同行的高度关注。
钱学森博士论文的第三部分《可压缩流体的二维亚声速流动》,是在寻求一种新的计算高速飞行的飞机机翼表面压力分布情况的科学方法,冯·卡门亲自指导了钱学森的研究,钱学森的研究成果以及冯·卡门在1941年发表的关于空气动力学中压缩效应的研究结果,被总结为著名的“卡门-钱近似”公式。
20世纪30年代末,飞机的发展出现了一个危险的瓶颈,就是当飞机以接近声速飞行时,气体会在机翼表面挤成一团,压力逐渐增加,从而导致失速,而失速问题已经连续几次带来了机毁人亡的严重事故。在提高飞机飞行速度的努力中,机翼的空气压力分布计算遇到了前所未有的困难。航空界已有的一些计算方法,只能适用于飞机机翼较薄、飞行速度较慢(例如小于0.5倍声速)的情况。为了实现大型超声速飞机精准合理的设计与制造,冯·卡门凭着对物理问题敏锐的洞察力,建议改变传统的计算方法,采用来流状态点处的切线近似计算法。钱学森在导师的启发下,专心致志地反复对比、思考,加以一系列严谨的数学推导、计算与实验。那时还没有电子计算机,他的手工计算通宵达旦,常常一伏案就是十几个小时。这一研究成果成为钱学森在加州理工学院的代表作,他终于证明,虽然和前人一样都是作切线近似计算,但采用他和老师发明的来流处的切线近似,可以计算出比过去更为精确的空气在机翼表面高亚声速流动的数据。
通俗地说,“卡门-钱近似”公式第一次揭示了在可压缩的气流中,机翼在亚音速飞行时的压强和速度之间的定量关系,准确地表达了当飞机的飞行速度接近每秒为340米的声速时,空气的可压缩性对机翼和机身升力的影响究竟有多大。利用这个公式可以在整个亚声速范围内,比较精确地估算出翼型上的压力分布,同时还可估算出该翼型的临界马赫数值。“卡门-钱近似”公式,是空气动力学的一项重大科研成果,也是世界航空业界的传世经典。在第二次世界大战期间以及第二次世界大战之后很长一段时间内,这一计算方法被世界各国广泛应用于超声速飞机设计与制造,为航空工业的发展提供了莫大的帮助,直到现代电子计算机实现应用。钱学森的同事史密斯曾这样评价这一神奇的公式:“每个飞机设计师都必须应用它,它在工程界的服务卓然有成。”
钱学森博士论文的第四部分《以逐次脉冲推进的探空火箭飞行分析》,是在探讨采用什么样的发动机和燃烧方案,可以使火箭经济而高效地达到更高的速度和高度。当时他参加了同学、好友马林纳组织的火箭研究小组,在小组里负责理论计算的任务。当时,火箭还是个新事物,整体技术水平不高,有关权威根据传统的静态燃烧试验得出的结论是,火箭至多只可以达到3 000米的高度。可是这个高度距离“探空”的目标相差甚远。钱学森和马林纳不信邪,他们另辟蹊径探讨和论证了逐次推进的方案,即采用以硝化棉一类的固体火药作为推进剂,进行多次快速燃烧排气而获得脉冲式推力的方案,这样火箭完全可以达到30 000米左右的高度。在这个高度上,就能够顺利地开展大气层的结构以及稠密大气以外的物理现象的观测和研究。
三年寒窗苦读后,钱学森以其水平很高的博士论文顺利地获得了博士学位,并被聘任为学院的助理研究员,从冯·卡门的学生成了他的同事。
1939年的冬天,雨丝绵绵,似云似雾,像轻纱一般飘浮在清冷的寒风中,为加州理工学院披上了一身雾装。
钱学森和冯·卡门一起站在古根海姆办公大楼前。
冯·卡门皱着两撇浓眉,望着满眼的朦胧,心情沉重地对他的爱徒说:“钱,前线的飞机在向我们提问了。”
原来第二次世界大战开战后,空军的重要作用日益明显,交战各国已经淘汰了速度很慢的活塞式、布蒙皮双翼飞机,都在想方设法采用薄而轻的金属制造飞机的壳体。但是,如果高速飞行的薄壳结构载荷超过一定数值,壳体就有可能发生皱瘪而失稳,即产生“屈曲”现象。这样,飞机结构就会失稳以至完全破损、折戟沉沙。设计师急切需要知道发生“屈曲”的临界载荷的数据。然而,当时只有前人依靠经典线性理论计算出来的数值,与实验值几乎差了3倍至4倍,无法应用。人们只好凭借经验去设计薄壳金属飞机,因此成功率很低。
冯·卡门深知解决这个难题在第二次世界大战中的重大意义,于是鼓励钱学森尽快研究解决“薄壳失稳”的问题。
钱学森接受了老师交给的又一道难题。
从1940年到1942年,钱学森经常把自己关在古根海姆大楼三层的研究室里工作到深夜。有个当年的研究生回忆道:
有天一大早,好像是感恩节或圣诞节,我在学校赶功课,以为全幢建筑物里只有我一个人,所以把留声机开得特别响,还记得我听的是特别激昂的《时辰之舞》。乐曲高潮到一半时,有人猛力敲我的墙壁。原来我打扰到隔壁的钱学森了。我这才知道,中国学生比犹太学生更用功。后来他送我几份他写的关于可压缩流体压力校正公式的最新论文,算是对于曾经向我大吼大叫表示歉意。
1940年9月到加州理工学院进修的中国空气动力学者张捷迁恰好与钱学森合用一间研究室,有整整一年时间,几乎天天跟钱学森见面。他说:“钱学森跟我是好朋友。我们天天一块儿吃午饭和晚饭,有时工作紧张,吃罢晚饭就得回研究室继续工作。我很少待过午夜,但他不肯停止,即使过了午夜,他房间的灯还亮着。”
两年之内,钱学森潜心研究,完成了多篇探讨球体外壳、薄圆柱体外壳、实心柱等各种屈曲现象的论文,其中有《壳体屈曲的文献总结》,这是他对前人工作所做的总结和评述,共18页。通过文献总结,他剖析了前人理论的优缺点,搜集了能够得到的点点滴滴的实验数据,认为应当从有限挠度的弹性屈曲理论入手,采用能量法求取屈曲临界载荷。在这篇总结里,他大致勾勒了能量跃变准则的初步轮廓,但他认为这只是初步的研究结果,没有发表。
1940年,在冯·卡门的具体指导下,钱学森的研究工作有了进一步的深入,他发表了《球壳外压屈曲》论文。在26页的手稿上,工整秀气的字体是钱学森的,而飞逸花哨的字体则是他老师的,师徒二人的智慧浑然一体。
为了回答究竟多大载荷能使受压的球壳失稳这个问题,钱学森提出了一个新思路——经典理论之所以不适用,在于它没有考虑到,金属壳体在加载过程中除了保持球形位形外,还可能存在多个位能更低的其他位形。一旦壳体受到外界干扰,它就有可能被激发而发生位能的高低跃变。因此,设计师不仅要知道经典线性理论所给出的“上”屈曲载荷的准确数值,还要特别注意找出使壳体发生有限变形时“下”屈曲载荷的准确数值。由于钱学森的计算结果确实与实验值十分接近,这一新的发现和理论很快被学术界和工程界接受,成了飞机设计的主要依据。
1941年,钱学森把上面提出的计算屈曲临界载荷的能量跃变准则,又推广到应用更为广泛的柱壳领域。
柱壳体与球壳体产生屈曲现象的原理相同,但是求取屈曲临界载荷的计算却大不相同。钱学森建立理论模型,列出特征方程,寻找应力关系,制作演算图表,一步步推导,一行行计算,然后与实验结果反复对照。一次不满意,就推倒重来,他前前后后写了5份文稿。他的同事席尔斯回忆说:
有一次我到冯·卡门家中,只见冯·卡门跟钱学森正在讨论,他们似乎有些数学细节未能厘清,两人分头演算,得出的误差竟然还不小。我当然有兴趣知道大教授跟他的得意门生究竟谁对谁错,所以竖起耳朵听。他们从头开始核对,一行一行比较,结果两个人都对!只不过在计算到某个阶段时,他们选择了不同的方法。然后他们又从头开始讨论哪一种计算方法合适……
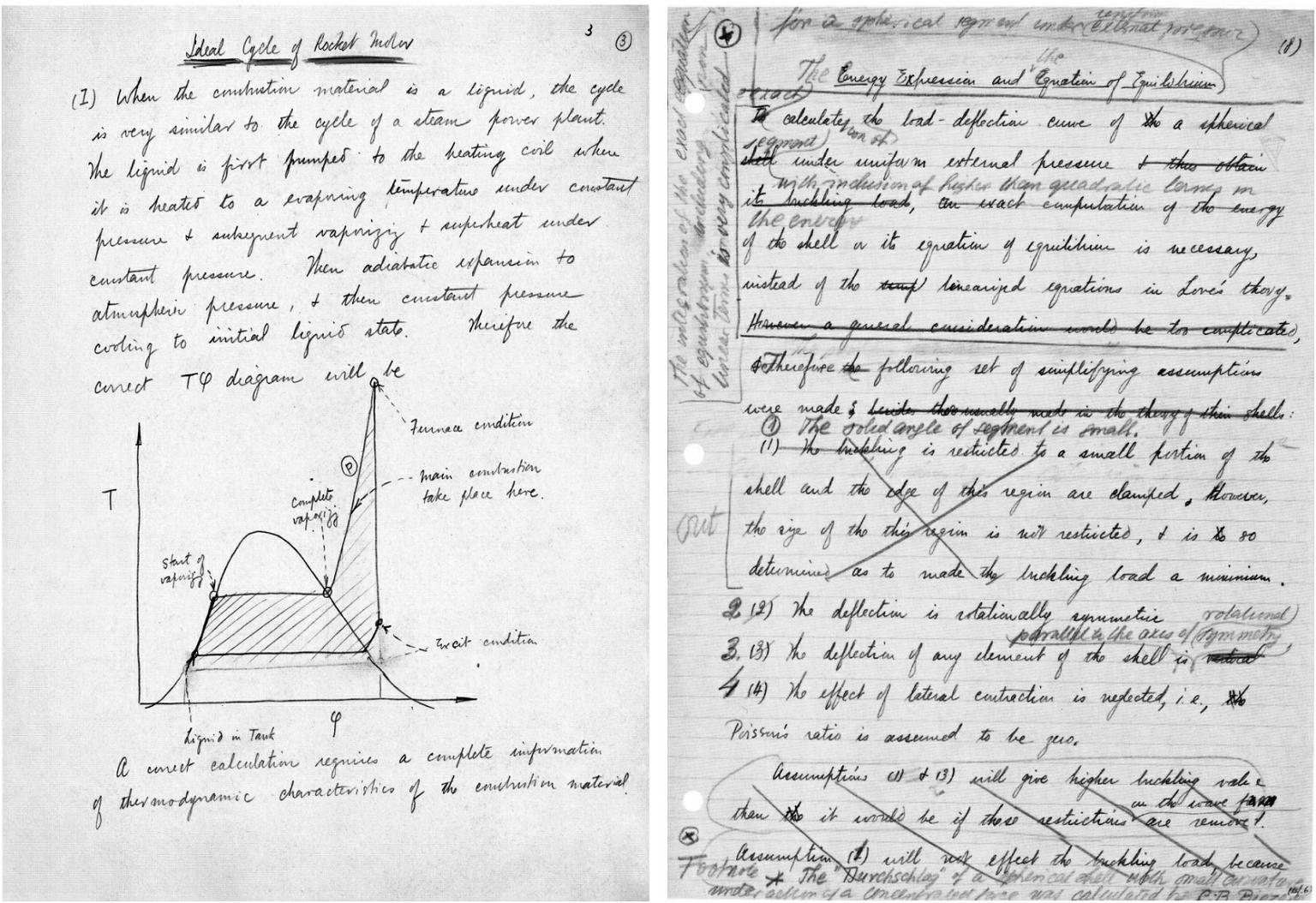
钱学森经冯·卡门修改后的论文手稿
钱学森的辛勤耕耘,震惊了航空界,也使他的老师为之兴奋得手舞足蹈。
冯·卡门亲自带领的研究生不只钱学森一个人,大家每周至少在冯·卡门家聚会一次,讨论航空学与数学。尽管冯·卡门门下人才济济,但他丝毫不掩饰对钱学森的偏爱,钱学森的同事马勃先生甚至有些嫉妒地说:“钱是老师最好的合作者,根据我跟他们一起工作的经验,只要他们两人在一起,就会有创新。”
有时,冯·卡门突发奇想,会迅速在黑板上写出一道难得不得了的方程式,然后扬长而去。一星期后,钱学森会一声不响地把整套棘手的方程算完,然后跑进来对同事们说:“冯·卡门的想法是对的!我算的结果真的就是这样!”在加州理工古根海姆实验室做航空工程学研究员的李普曼教授回忆道:“钱学森提高了冯·卡门的创造力,他杰出的数学技巧能在最短时间内把冯·卡门的观念付诸实现。”
钱学森从老师身上学到的一丝不苟、严谨求证的作风,使他并不满足于理论推导和纸面计算,必须用实验结果来验证他的结论。他在数学演算中发现,圆柱形外壳发生屈曲时,大多出现钻石形状。为了求证此事,他和同事们在校园航空大楼外搭了一个直径3英尺、长10英尺的金属壳,慢慢注满水,增加内部压力。水排泄出去后这个金属壳果然逐渐变形,表面出现许多钻石形屈曲。一位参加实验的校友拉索夫说:“理论预测跟事实完全符合。钱学森目睹他的理论经由实验证明,也大呼真不可思议。”
历时100多个日落日出,钱学森终于拿出了一份分量十足的论文《柱壳轴压屈曲》,1941年美国《航空科学学报》第8卷刊登了这篇论文。论文发表时只有短短的10页,可是钱学森为了凝练这10页,写下的演算草稿竟达800多页。想一想,现在我们一般人即使使用计算机抄录800页的文字,也要花费很长的时间,何况,当年的钱学森是在进行艰苦的创造性手工写作!
在完成了老师交给的难题后,钱学森终于长长地舒了一口气。他把800多页手稿装进一个纸袋里,并在纸袋外面写下了“Final”(最后的定稿)字样。但他立刻想到,认识是无止境的,真理是相对的,于是,紧接着又写了一行字“Nothing is final”(没有什么认识是终极的)。
钱学森关于薄壳体稳定性的研究,获得了了不起的研究成果,不仅对于高速飞机,而且对于火箭壳体的工程设计也具有非常重要的理论意义和现实意义。钱学森很快成为当时加州理工学院和航空界最惹人注目的人物。他具有开拓性而又有实用价值的研究成果,奠定了他在航空技术工程理论界的地位。钱学森毫无争议地进入国际知名学者的行列。

冯·卡门传记《风云际会》,其中一章专门叙述与钱学森的交往
此后10多年,钱学森与郭永怀合作,最早在跨声速流动问题中引入上下临界马赫数的概念。他们发现,对高速飞行真正有实际意义的是上临界马赫数,而不是以前大家所注意的下临界马赫数。这是一个重大发现。
钱学森首先提出了高超声速流动相似率,为高超声速飞行器的设计奠定了基础。
钱学森将稀薄气体的物理、化学和力学特性结合起来,对稀薄气体动力学进行了开创性的研究。
20世纪三四十年代,钱学森潜心钻研空气动力学和固体力学,为飞机的高速飞行和突破“声障”与“热障”不断探索,作出了全方位的重大贡献。
师从冯·卡门和与冯·卡门共事的那段时间,是钱学森生命中的一段欢愉时光。一向以严厉著称的冯·卡门对钱学森这个中国学生和同事既赞许又推崇,在几十年后出版的自传《风云际会》中,唯一用整章篇幅描述的学生就是钱学森。他讲述和钱学森的交往经历,并表示,有这个很有想象力、数学资质极高的学生做自己的助手,简直是可遇而不可求的。对钱学森而言,师从冯·卡门是他毕生最重要的学术生涯的升点,与冯·卡门共事是他光辉事业的起点。