




孔老夫子说:“君子矜而不争,群而不党。”这里,“群”指团结群众,与人和谐,“党”则是个贬义词。所谓党同伐异,结党营私,党恶佑奸,朋党之争,都表示将少数一群人的利益或观念置于大众和公民之上。中国老祖宗看重的,从来就是“天下”,全体人,文化能覆盖的所有地方和所有人。这是传统中国的开阔境界,视角高越的人类关怀。
希帕索斯(Hiappasus,生卒年月不详,活跃期在公元前470年左右)若能理解传统中国的思想境界,在加入毕达哥拉斯学派时或许会有所保留,也就能保全性命,免除杀身之祸?但历史没法假设。
他那样热衷于探索真相和智慧,精神独立又思想自由,认同赫拉克利特的“火是万物的本原”,他跟毕达哥拉斯学派的精神底色并不契合。
毕达哥拉斯学派是个什么样的存在?
毕达哥拉斯是哲学家、数学家,更是导师和“教主”。他在意大利半岛南部定居后建立的这个学派,有学术之名,也有宗教色彩,还有秘密组织的形式。
没有人能否认毕达哥拉斯学派的历史功绩,他们作为“合理而牢固地联系在一起的一般观念体”,对数学这门学科的影响也相当深远,“以一种有计划的方式在整个世纪发生影响”。正是受其影响,希腊数学长期偏重于几何,以至于所有的代数问题,包括最简单的一次方程,都要用几何方式求解。数学界的这种格局和模式,直到丢番图(Diophantus,约246—约330,代数学的创始人之一)出现才得以扭转,那已经是800年后的事了。
而且,毕达哥拉斯学派支持女性从事科学研究,一开始就有女信徒,毕达哥拉斯的妻子是当时有影响力的数学家。单这一点,就胜于同时代的孔子和释迦牟尼。
但是,相较于科研团体,封闭的毕达哥拉斯学派更像是社会团体和宗教神秘组织。他们内部有严密的组织和纪律、很多秘密仪式和苛严戒律,甚至充斥诡异的气氛。这多少有点儿像中国的墨家。
加入组织的新人要宣誓效忠,永不加入其他团体,永不向外界透露任何内部秘密和学术成果,否则会被处死。新入伙的没资格见到“教主”,先被毕老师关在门外“听课”一段时间,通过组织考验和考核,才能登堂入室拜见“教主”。
在这个严重“自闭”的团体内部,所有人禁欲、苦行,保持整齐划一的生活方式。有些离奇的禁忌,我们现在已经很难理解。比如不吃肉、动物内脏和豆子(因为豆子形似睾丸,会引人想入非非、误入歧途),不能用刀拨火,面包不能掰开吃,得啃着吃。
教派内的所有财产公有,科学发明也公有——所谓公有,现在看起来,就是归在毕达哥拉斯一人名下。学派取得了不少成绩,第一对亲和数220和284、cosmos(宇宙)这么重要的词、现在运用过滥的“黄金分割”,这些很大概率是“集体智慧的结晶”,哲学史家劳特利奇(Routledge)甚至怀疑毕达哥拉斯本人毫无数学创见,连“毕达哥拉斯定律”都应该是“毕达哥拉斯学派定理”。
但在现实中,毕达哥拉斯学派往往“简称”为毕达哥拉斯,包括学派取得的成果。正如我们不知道《吕氏春秋》各篇的作者,只能记住书名上的那个人——吕不韦。一切荣耀都归于他。
毫不奇怪,学派里的一切都带着毕教主的个人色彩。而世上有这样一种人类基因:秉性顽强、坚定、自信、聪明、富有感染力,但恰恰因为太坚定自信,以至于狭隘、僵化、绝不通融,容不下异己;又因为有感染力和领导力,所以善于拉帮结派、党同伐异,容易成为一群狂热之徒的精神导师或事实上的领袖。
具有这种基因的人,在政治领域可以是独裁者,如希特勒;在宗教界是血腥残酷的革命者,如加尔文;在学术圈则可能是学阀和学霸。
毕达哥拉斯恰好是这样的人。
我从不假装自己喜欢他,就因为他那么完全地属于组织,这个组织又那么严密。太过严密的组织必然扭曲人性。在毕达哥拉斯心里,在毕达哥拉斯学派内部,最高原则从来不是人性,也不是真理,而是毕教主认可的价值,美其名曰“理性”。
他认定人类区别于其他动物,不在于智力和热情,而在于理性。所以他强调人在日常生活、感情表达方面都应该节制。然而,做自己感情的奴隶,比做暴君的奴仆更不幸。任何草率的行为、冲动的言辞,都被他称为“卑劣”,他说“愤怒总是以愚蠢开始,以后悔告终”“不能制约自己的人,不能称之为自由的人”。我猜度他的自律和节制应该让人生敬甚至生畏。
但一个人有多自律和节制,往往就有多执拗和冥顽不化。人固然需要自律,但自律太过也有隐患。毕竟能贯彻“严于律己,宽以待人”原则的人可谓凤毛麟角,于是,如果一个人为了遵守理念对自己都这么狠,就很难预计他对别人会多狠。
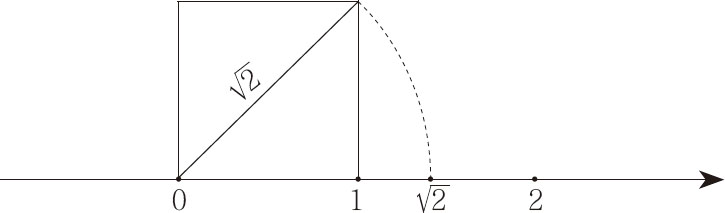
无理数是有理数之间的“坑”
事实证明,毕达哥拉斯能狠到取人性命不眨眼的程度。
当毕达哥拉斯学派说“万物皆数”时,他们所谓的“数”是整数,或者整数之比(分数),在他们看来,数美丽和谐、精确可控。宇宙依据数字而构建,也美丽和谐、精确可控。
据亚里士多德说,毕达哥拉斯本人已经意识到,边长为1的等腰直角三角形,斜边的长度是一个神秘的、无限的非整数——
 。因为这个数将动摇整个数学的根基,它变成了学派内的最高机密和最大忌讳。
。因为这个数将动摇整个数学的根基,它变成了学派内的最高机密和最大忌讳。
希帕索斯却发现了这个秘密,他大为惊奇,开始热情地思考和讨论它,还妄想将它镶入数学体系中,为此不惜拆装毕老师已经“建成”的数学大厦的整体结构。
就是这一点,碰了毕老师的底线。数学大厦岂容你想拆就拆,拆散了组装不起来怎么办?你让一帮以数为信仰的人,到哪里再去寻找灵魂的圣殿和精神的避风港?总之,这是一个致命的数字。它的存在毫无道理,最好的办法,就是让它不存在。
数字无法消灭,就只能消灭知道这个数字的人。希帕索斯在探索真相的道路上走得太远,既不肯闭目塞听不思考这个数,又不肯装聋作哑假装没有这个数。既然他不肯停止思考,自然只能让他灭亡。
关于希帕索斯的死有不同的说法:有的说他风闻学派下达了追杀令,仓皇登船而逃,遭遇海难身亡;也有的说他在出逃路上被学派教徒抓获,直接扔进了大海。不管怎么说,他都是因为
 而丧生大海。
而丧生大海。
从现有资料来看,因无理数而死的人很可能还不只希帕索斯一个。古希腊数学家普罗科拉斯在给欧几里得《几何原本》作注时写道:“据说,首先泄露无理数秘密的人全部都丧了命,因为对所有不能表达的和不定型的东西,都要严守秘密,凡是揭露和过问的人,必会遭到毁灭,并万世都被永恒的波涛吞噬。”
重点是那个“都”字。死于一个数字的人并不只希帕索斯一人,他只是留下了名字而已。
所幸,“数字无法消灭,就只能消灭知道这个数字的人”这句话,也能反过来说,发现无理数的人可以“都”被杀戮,但无理数永远没法被消灭,总会不断被重新发现。
无理数的发现,连同芝诺悖论,终于引发了人类科学史上的第一次数学危机。
多介绍一句芝诺,他提出了关于运动的四大悖论,其中最有名的是“阿基利斯追不上乌龟”和“飞矢不动”。而芝诺和老师巴门尼德都曾经是毕达哥拉斯学派的信徒,真是“祸起萧墙”。
无理数危机爆发后,不断有数学家尝试化解,据欧几里得《几何原本》第五篇记载,公元前370年的欧多克斯提出迂回曲折或者说自欺欺人的解决方式:无理数被允许在几何中使用,但在代数中却是不合逻辑和非法的。也就是说,无理数只是一种量度中的符号,而不是真正的数。
如此强行剥离数和量的鸵鸟手法,或许可以暂时安慰数学家们受伤的心,但并没有真正解决问题。随着新的无理数(如圆周率)被不断发现,拥护无理数存在的人越来越多,无理数也变成了一个必须直面和解决的问题。
直到1872年,德国数学家戴德金用“有理数的分割”来定义无理数,并建立起实数理论,无理数在数学世界才算被“扶正”,获得了合法地位。无理数引发的第一次数学危机,持续了两千多年后,至此圆满化解。
希帕索斯们的灵魂,若还漂浮在地中海的水面上,此时不知是微笑还是伤感。或许他最痛的彻悟,是每一个自由求知的灵魂,都需要保有完整和独立的自我,一定要慎入各种派别,越严密的派别越要警惕,因为严密必然只是组织的成功,也必然以牺牲个体和个性为代价。
只有菠萝派和香芋派可以例外。