




毕达哥拉斯(Pythagoras,约前580—约前500)的代表性成果是毕达哥拉斯定律。这个平生最大的成就也带给他最大的打击,几乎摧毁他的信仰大厦,让他感受到毕生无法面对的痛苦和恐惧。
据说这个定律是这样诞生的:某一天毕达哥拉斯去赴饭局,但不知道为什么,主人迟迟不开饭。等饭的毕达哥拉斯百无聊赖,看着餐厅同样的正方形地砖发呆,慢慢地看出神,看出门道来了:
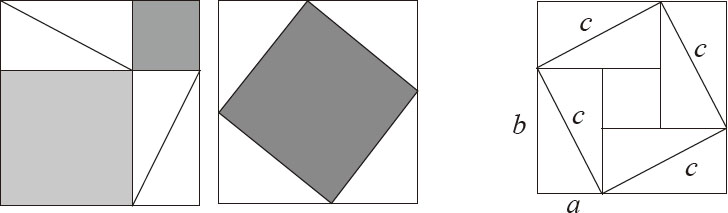
以任一正方形地砖的对角线为边长,画一个大的正方形,其面积正好是两块地砖的面积之和;如果以两块地砖组成的矩形之对角线为边长,得出的正方形面积是五块地砖的面积;以三块地砖的对角线为边长构成的长方形,面积是十块地砖的面积……他由此得出结论: a 2 + b 2 = c 2 ,直角三角形的两直角边的平方之和,等于斜边的平方。
毕达哥拉斯对这一发现很是骄傲,杀了一百头牛来庆贺(要知道,毕达哥拉斯可是严格的素食主义者),所以著名的毕达哥拉斯定律在当时被称为“百牛定理”。
毕达哥拉斯定律是人类最早得到论证的平面几何定律之一,也是最广为人知的数学定律之一,就连童话故事《绿野仙踪》里的稻草人,也以“明白了毕达哥拉斯定律”来表示自己智商有所提升。1955年,希腊发行过一张纪念邮票,用三个正方形拼出一个直角三角形,被称为“新娘椅”,集邮的人都知道该邮品的珍贵。
其实,有充分的考古证据表明,在毕氏之前近一个世纪,古巴比伦人已经掌握这一定律。中国人也会强调《周髀算经》里记载的“勾三股四弦五”,这可比毕达哥拉斯早半个世纪,知识产权据说属于中国最早有确切记载的数学家、周公智囊团成员商高(也叫殷高,因为他生活在由殷商入周那段时期)。
不同的是,古巴比伦人和中国人得出结论,都只是大量经验事实的归纳总结加上假设,是思考的初级阶段,毕氏却秉承泰勒斯的做派,用逻辑给出确切的论证。他明确说过:“在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。”单凭这一句语,荣誉也该归于他。
说了这么多,都是为了证明,毕达哥拉斯定律有多么了不起,是毕达哥拉斯及其学派的学术代表作和象征。
可是,知我罪我,成败皆萧何。正是这个具有代表性的定律,最终给了毕达哥拉斯毁灭性的一击,几乎导致毕达哥拉斯学派理念的“崩溃”。
问题出在简单的直角等边三角形的论证上,设直角边都是1,很轻松地得出斜边的平方是2,可这个斜边
 到底是多少?优秀的数学家毕达哥拉斯算出来一个无法理喻的数字:1.41421356……。无穷无尽。
到底是多少?优秀的数学家毕达哥拉斯算出来一个无法理喻的数字:1.41421356……。无穷无尽。
隔着两千多年的时光,我都能感觉到毕达哥拉斯背脊的森森凉意和内心的巨大恐惧。
在这之前,人类理解的“数”都恒定确切。现在,他居然无可辩驳地证明了:世界上存在一种不成比例、说不清楚到底是多少的数。他对这一发现毫无思想准备,他坚不可摧的数字系统里,也没有为无理数预留任何空间。数字竟然会不确定?世界也不再确定和精准。这是多么可怕的结论啊!
之后,人类又陆续发现了更多的无理数,圆周率π=3.14159265……,黄金比例是0.61803398……,e=2.71828182……都是没完没了、无法确定的数字。
数字的伤害性能有多大?你也许觉得,不要矫情啊,数字而已,至于吗?
还真至于。
这涉及三观和信仰问题。毕达哥拉斯及其学派的最高信仰是:万物皆数。他们对数字有奇怪的嗜好和坚定的信仰,相信整个宇宙都是按照数字模型设计并运转的,数是宇宙的程序和节奏。
美不是什么说不清道不明的感觉,而是黄金分割线;音乐不是什么美妙的声音或转瞬即逝的灵感,而是数字:一根弦,指尖摁在不同的地方,弹出的声音不同,这些声音可以直观地标注为弦上下部分的比例。所以古希腊神话里的九位缪斯(希腊语Μουσαι,拉丁语Musae,英语Muses)被称为艺术女神,也是音乐(music)一词的词根,其实她们还掌管科学。一个事实是,数学头脑好的人,学音乐很容易上手,反之亦然。
正因为此,毕达哥拉斯学派才会宣称:“一切都源于数”(正如泰勒斯说“一切源于水”)、“数统治宇宙”、“数学支配宇宙”。因为数和谐,整个宇宙才内在统一。而从公理出发,运用逻辑推演,可以不容置疑地达到宇宙任何真相的角落。了解了“数”,就了解了“宇宙”,这个结构完整、严丝合缝的世界。
而他们说的“数”,仅仅只是——用今天的术语表达——有理数。
在形成“万物皆数”“灵魂不灭”的思想之后,他们却不得不面对无理数,也就是无理的世界!所谓世界观崩塌、信仰全失,说的就是这种情况。
“无理数”这个名词就很说明问题:没有道理的数字,不讲道理的数字。
整数、分数、0,那都是“好学生”,有规矩、讲道理、成比例(“有理数”的希腊文λογος,原意就是rational number,成比例的数)。而无限不循环的数,不能用两个数的比来表示,真是很没有道理,像调皮捣蛋鬼一样不靠谱、没定准,让人悬着心。数本来应该像焦仲卿的誓言一样,磐石方且厚,可以卒千年。无理数却不精准、不稳定、捉摸不定,让人没有安全感。
这么一想就会明白,无理数的出现让多少人心碎!它不仅是对毕达哥拉斯学派的致命打击,甚至无差别攻击了全体希腊人的心灵。一个数,无限,又不循环,永远不能绝对精确地呈现。对于追求理性、逻辑、周密和严整的人来说,是一个多么有破坏性的存在。它无视人的心理需要,导致严重的认知危机。
面对无理数,毕达哥拉斯认知破碎信仰坍塌。他理解和信仰的数是这样的,数字的真相却是那样的。他一心要建万年基业亘古稳定,无理数却“背叛”了他,让他的整个世界根基松动、摇摇欲坠。情何以堪?
为了解释清楚毕达哥拉斯的心碎,我需要多举几个例子。事实上,无理数的发现只是数学界三次危机的第一次。
其后,英国的主教哲学家贝克莱(George Berkeley,1685—1753)证明无穷小既等于零又不等于零,几乎毁灭了微分和积分。
美国的加州大学就是为了纪念他,将创始校区命名为加州大学伯克利分校(University of California,Berkeley),该校是世界著名的大学之一,在各类世界高校排名中都名列前茅,志向远大的同学可以考虑报考或是去进修。
接下来,罗素引发了第三次数学危机,又一次伤害了数学和逻辑大厦,还差点儿震翻哲学界。
一直以来,逻辑是西方人精神的避难所、真理的休憩地、智慧的神圣殿堂、检验真理的最高标准。弗雷格(Friedrich Ludwig Gottlob Frege,1848—1925,德国数理逻辑和分析哲学的奠基人)的工作就是试图证明数学跟逻辑一样,是一门高度抽象和超验的学科,不依据经验和实践,纯以逻辑推演构建而成。
弗雷格用十多年的时间终于完成了这项浩大工程,在《算术的基本法则》即将出版时踌躇满志地宣布:算术是分析判断,因而是先验的。这样算术就会仅仅是一种扩展形成的逻辑,每一个判断都是一种逻辑定律,或是其推演物。在科学中应用数学就是在观察到的事实中应用逻辑关系。计算就是推理。
就在这个节骨眼上,小年轻罗素(Bertrand Russell,1872—1970,分析哲学的主要创始人)来信了。这封信被弗雷格称作“罗素炸弹”,其实罗素只是在前人基础上提出的罗素悖论,其最著名的通俗化演绎就是“理发师悖论”:理发师只给那些不自己剃头的人剃头,那么他给不给自己剃头?
简单地说,弗雷格证明了算术是纯粹的逻辑,罗素却告知,逻辑学不合逻辑。
弗雷格的半生心血,顿时碎成渣渣。他最终还是咬着牙出版了他的著作,但在书后加了一段痛苦的自白:一位科学家不会碰到比这更难堪的事情了,即在工作完成之时,它的基础垮掉了,当本书等待印出的时候,罗素先生的一封信把我置于这种境地。
数学并不是唯一遭受过这种残酷打击的学科。人类科学史上,类似的毁灭性事情还发生过多起。
当生物、地质、考古等学科证明了地球上的物种是演化的、有生有灭时,不知道有多少安歇在上帝精神殿堂里的科学家(注意:是科学家,而不是牧师或普通信徒)感到难以忍受。
物理学更是数学的难兄难弟。相对论敲碎了牛顿的经典物理世界,量子力学又深深伤害了相对论。
在经典物理学被证明有限之后,德高望重的荷兰物理学家洛伦兹(Hendrik Antoon Lorentz,1853—1928)痛切地哀叹,他为什么没有在世界坍塌前几年死去?!这样就不至于在思想的地震中,眼睁睁看着自己毕生努力构建的理论大厦毁于一旦——其起因不过是大厦底部的一小块砖头被抽掉而已。
一切都像罗素说的,“虔诚的天主教徒遇到了邪恶的教皇”。发明带来的不是欣喜和成就感,而是恐慌:经过多年经营、无数代人的艰难探索,一个完美和谐的世界眼看大功告成,逻辑自洽,美丽动人,功德圆满,固若金汤。可是,只需要一点点多余的发现,一个不经意的小破绽,整个帝国大厦就轰然坍塌。说崩就崩,一点儿没商量。
真理好生无情,只管自顾自地“青山遮不住,毕竟东流去”,徒留下真理探索者们。弃我去者,昨日之美丽世界不可留;乱我心者,今日之断垣残壁多烦忧;明日之美丽新世界,又遥遥无期如海市蜃楼。老天!到哪里去安顿和拼装那些被撕裂了的人类思考?
从无理数,到数理逻辑,到量子力学测不准定律,人类在追求完美和确定的道路上一再遭受致命打击,世界飘摇不定,找不到永恒确切的真理。无论你得到多么严密的真理,它的背后总藏着另一个相反的真理,也许,这才是宇宙的真相?
人类或许可以设法自我安慰,只有不确定性才能保证人类的自由意志。但是,真理的确定性和自由的可能性,都是根植于人性深处的本质需求,非要分出哪个更重要吗?
真正的问题终于出现了:越是令人难以承受的真相,越是对心灵的锤炼和对精神的残酷考验。是勇于面对、自我修正,还是消极回避、掩耳盗铃?这是真伪科学家的分界线。
而毕达哥拉斯,很遗憾地做出了反科学精神的选择。
毕达哥拉斯被罗素说成“历史上最有趣又最难理解的人之一”,他年轻时远赴米利都,投在泰勒斯门下,那时泰勒斯已经很老,所以有说他多半是跟着泰勒斯的大弟子阿拉克西曼德学习,之后又游学巴比伦和埃及。应该说,他的学识和见识是开阔的,不开阔的只是他的心。
无理数是毕达哥拉斯的重要发现,本来是一个通向数学新世界的洞口,他却没有勇气和能力去面对。他用一具尸体堵住了那个透光的洞口,留下一个关于谋杀的历史谜案。人类历史上第一次,有数学家因为自己的思考而死于非命。
入我门,就要听我话,疑我世界,就取你性命。毕达哥拉斯创建了学派,也决定了这个学派的氛围、传统和组织原则,这个组织的可怕,你马上就将看到。