




燃料电池运行过程中,燃料氢气和氧化剂氧气的消耗与输出电量之间的定量关系服从法拉第第一定律和法拉第第二定律。
法拉第第一定律:燃料和氧化剂在电池内消耗质量Δ m (kg)与电池输出的电量 Q (C)成正比,即

式中, k e 是比例因子,电化当量(kg·C -1 ); I 是电流强度(A); t 是时间(s)。
法拉第第二定律:通电于若干个电解池串联的线路中,当所取的基本粒子的荷电数相同时,在各个电极上发生反应的物质,其物质的量相同,析出物质的量与其摩尔质量成正比。其数学表达式为

式中, n 是反应转移电子数; F 是法拉第常数(C·mol -1 ); M 是摩尔质量(kg·mol -1 )。
综合式(2-25)和式(2-26)可以得到,燃料和氧化剂在电池内消耗的物质的量Δ N (mol)与电流 I (A)之间的关系为

法拉第第一定律和第二定律反映了燃料和氧化剂消耗量与其本性之间的关系。氢燃料电池中每输出1 F 的电量(26.8A·h),必须消耗1.008g氢气和8.000g氧气。
电化学反应速率 ν (mol·s -1 )定义为单位时间内物质的转化量:

电流强度可以用来表示任何电化学反应的速率。
电化学反应均是在电极与电解质的界面上进行的,因此电化学反应速率与界面的面积有关。将电流强度 I 除以反应界面面积 S (m 2 ),得到电流密度强度 i (A·m -2 ),即单位电极面积上的电化学反应速度:

评估一个反应的总速率时,要同时考虑正向速率和逆向速率。净速率为正向反应和逆向反应之间的速率差。对于同一半电极反应,例如式(2-1)中的氢氧化半电极反应或式(2-2)中的氧还原半电极反应,在平衡条件下,正向反应的电流密度和逆向反应的电流密度都为 i 0 ,称为交换电流密度。远离平衡态时,可以将新的正向电流密度或逆向电流密度理解成由 i 0 开始并考虑正向活化能垒和逆向活化能垒的变化,以及电极处反应物和生成物浓度的影响。
正向速率 i 1 :

逆向速率 i 2 :

净速率 i :
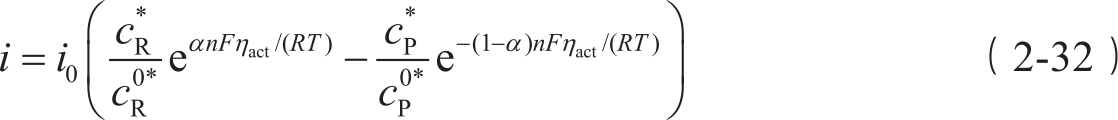
式中,
α
是传输系数;
η
act
是电压损失;
n
是电化学反应中转移电子数;
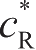 和
和
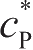 分别是反应中反应物和生成物的实际表面浓度;
i
0
是参考点处测量交换电流密度,此处反应物和生成物的浓度分别为
分别是反应中反应物和生成物的实际表面浓度;
i
0
是参考点处测量交换电流密度,此处反应物和生成物的浓度分别为
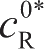 和
和
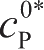 。
。
式(2-32)即被誉为电化学动力学奠基石的Butler-Volmer方程。该方程阐述了电化学反应产生的电流随活化过电位的增加呈指数型增加这一现象。活化过电位( η act )表示克服电化学反应相关的活化能垒而损失的电压。
当处理燃料电池反应动力学时,Butler-Volmer通常过于复杂。为了使用和计算方便,在特殊条件下可近似简化Butler-Volmer方程。
例如,在活化过电位很大时,Butler-Volmer方程中的第二项指数项可以忽略。此时,正向反应方向起决定作用,相当于一个完全不可逆反应过程。不考虑电极表面处反应物浓度影响,Butler-Volmer方程可简化为

通过该方程可以得到:
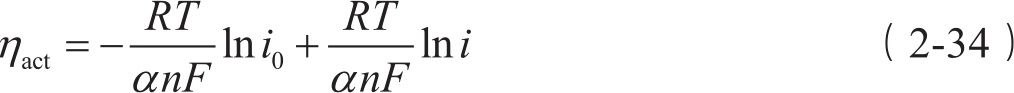
因此,活化过电位 η act -ln i 曲线应该是一条直线。通过拟合 η act 对ln i 可以获得 i 0 和 α 。可将式(2-34)概括为

该式称为Tafel方程,其中 a 为Tafel方程曲线截距; b 为Tafel方程曲线斜率。
对于燃料电池,需要注意大量净电流产生时的情况,此时 η act 值很大,可以认为是正向反应占主导地位的不可逆过程。因此,Tafel方程在大部分讨论中被证明是合理且有意义的。不过在较低的过电位条件下,Tafel方程的近似结果将偏离Butler-Volmer方程。