




拉普拉斯变换有许多有用的性质。比如,拉普拉斯变换可以把积分和微分变成算术运算,使交流电路的计算变得简单。再比如,利用拉普拉斯变换的终值定理,可以容易地算出时域信号在 t →∞时的值。本小节讨论拉普拉斯变换的其他三个性质,即线性、延迟和卷积的性质。这些性质都可以容易地用拉普拉斯变换定义式证明。下面来具体说明。
线性定理就是服从叠加原理。在线性电路中,两个信号源共同作用时在某支路内产生的电流或电压一定等于两个信号源单独作用时在该支路内产生的电流或电压之和,这就是电路中的线性定理。从拉普拉斯变换的式(4.2)看,由于积分是一种线性运算,拉普拉斯变换就一定具有线性性质。下面来证明。
假设用两个常数 a 1 和 a 2 把时域信号 x 1 ( t )和 x 2 ( t )组成线性组合 a 1 x 1 ( t )+ a 2 x 2 ( t )。对这个线性组合,用式(4.2)计算拉普拉斯变换
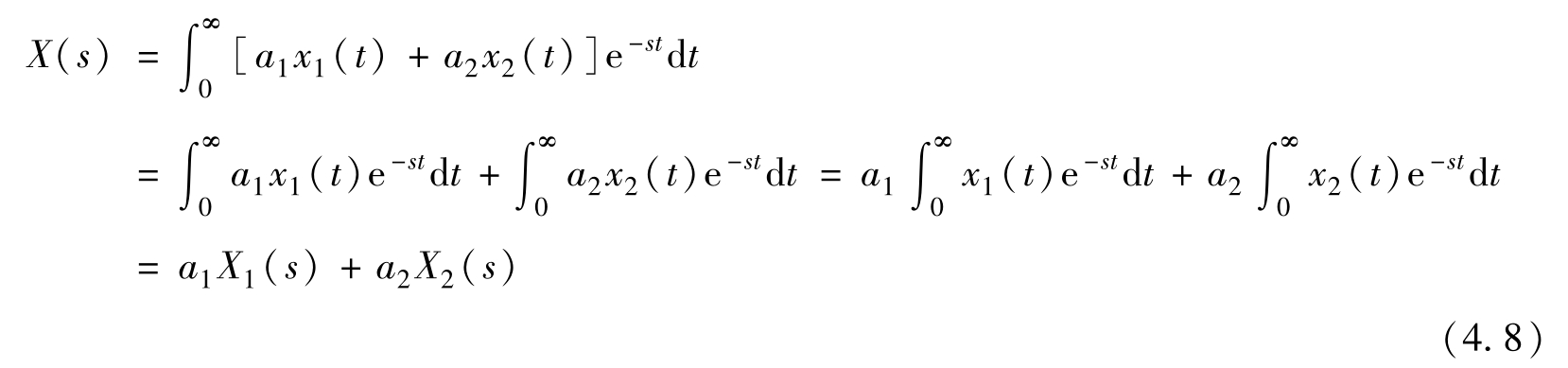
这就证明了拉普拉斯变换的线性定理,即两个时域信号 x 1 ( t )和 x 2 ( t )线性和的拉普拉斯变换等于这两个时域信号的拉普拉斯变换 X 1 ( s )和 X 2 ( s )的线性和。拉普拉斯变换的线性定理是被经常用到的。
小测试 : 计算信号3 δ ( t )+5 u ( t )的拉普拉斯变换。答:3+5/ s ,收敛域为不含虚轴的右半 s 平面。
现在把图4.1b中的单位阶跃信号 u ( t )右移时间 T ,变成 u ( t-T ),如图4.3所示。 u ( t-T )的拉普拉斯变换可根据式(4.2)写为

令变量代换 t-T = τ ,就有 t = τ + T 和d t =d τ ,而被积函数从 u ( t-T )变成 u ( τ ),同时积分下限从 t =0变成 τ = -T 。但由于 τ <0时总有 u ( τ )=0,积分下限就可以从 τ = -T 右移到 τ =0。式(4.9)可演算为
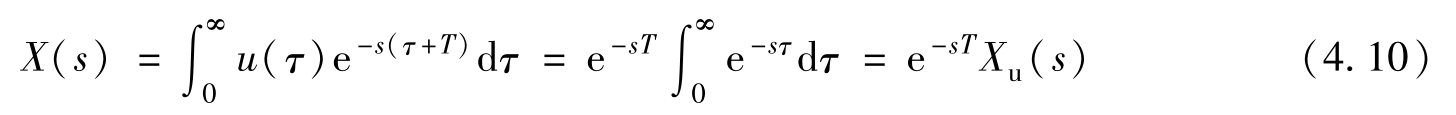
式中, X u ( s )为单位阶跃信号 u ( t )的拉普拉斯变换, X u ( s )=1/ s [式(4.10)运算中,积分变量 τ 只在积分式内部被使用,积分完成后随即消失,所以对积分结果毫无影响]。
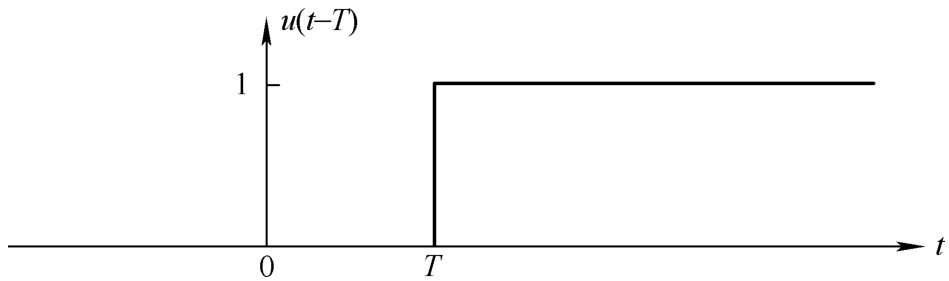
图4.3 单位阶跃信号 u ( t-T )的时域波形
式(4.10)表示,把时域中的单位阶跃信号 u ( t )右移时间 T ,结果是使它的拉普拉斯变换增加一个因子e -sT 。这就是拉普拉斯变换的延迟定理,并可叙述为:一个时域信号延迟时间 T 对应于它的拉普拉斯变换乘以e -sT 。书中后面的内容中将会看到,这个延迟定理可以容易地移植到 z 变换中。
卷积是信号处理中的重要操作,滤波器所执行的就是卷积操作。做卷积的前提条件是:系统是线性(Linear,L)和时不变(Time Invariant,TI)的。系统是线性的,表示满足叠加定理,而时不变表示系统特性不随时间而变。我们一般遇到的数字滤波器和离散时域系统都是线性和时不变的(Linear Time Invariant,LTI)。
本小节讨论拉普拉斯变换的卷积定理,并可叙述为:两个时域信号卷积的拉普拉斯变换等于这两个时域信号的拉普拉斯变换之积。下面先说明如何做时域卷积,然后证明卷积定理,最后用一个例子说明卷积的计算过程。
图4.4表示两个连续时域信号 x 1 ( t )和 x 2 ( t )的卷积计算过程。为便于讨论,我们假设当 t <0时 x 1 ( t )和 x 2 ( t )都等于零,如图4.4a所示。图中的 x 1 ( t )和 x 2 ( t )可以分别看作模拟滤波器的输入信号和单位冲击响应,而两者的卷积 y ( t )就是模拟滤波器的输出。下面先说明卷积的计算过程,然后给出卷积表达式[所谓单位冲击响应 h ( t ),就是当输入为单位冲击信号 δ ( t )时的系统输出,这已在前面讲过。由此可知,输入信号 x ( t )与单位冲击响应 h ( t )之间的卷积就是系统的输出 y ( t )。这就是图4.4中要说明的]。
在做卷积之前,先要把 x 1 ( t )和 x 2 ( t )的自变量 t 改为 τ (或其他任何变量名);而把 t 用作卷积 y ( t )的自变量,见图4.4c(改换变量名,不会改变函数的任何性质)。
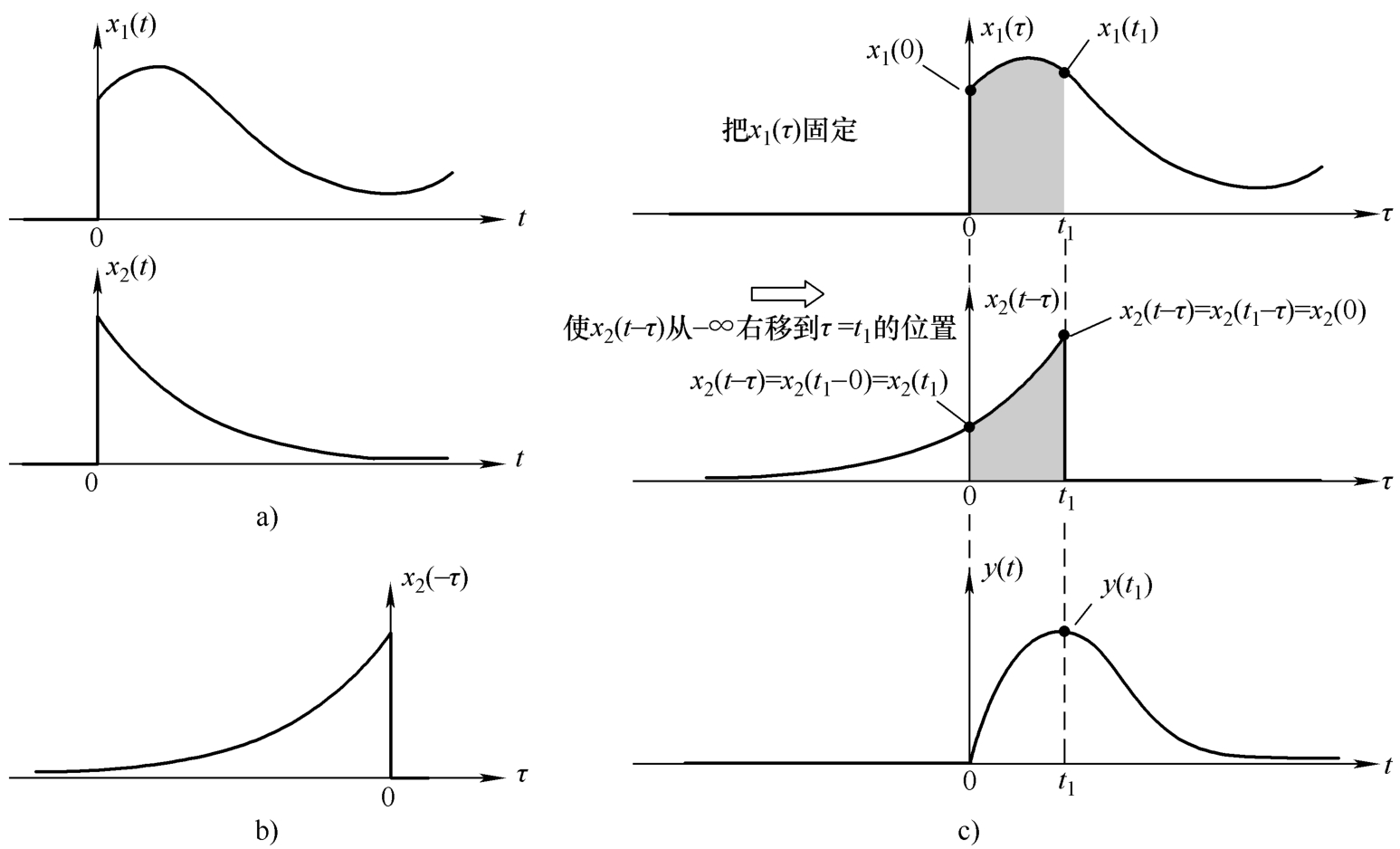
图4.4 计算两个连续时域信号 x 1 ( t )和 x 2 ( t )的卷积 y ( t )
卷积的第一步是把其中的一个信号在时间上倒转。在图4.4b中,我们把 x 2 ( τ )倒转,变成 x 2 ( -τ );而 x 1 ( τ )保持不变。我们也可以保持 x 2 ( τ )不变,使 x 1 ( τ )倒转,计算结果是一样的。
卷积的第二步如图4.4c中所示。先把时间上倒转的 x 2 ( -τ )改写为 x 2 ( t-τ )[这个 t 就是图4.4c中 y ( t )的 t ],这就可以通过改变 t 使 x 2 ( t-τ )左右平移[现在的 t 是参量, τ 是变量;如果 t =0,就得到图4.4b中的 x 2 ( -τ )]。现在令 t =-∞,就把 x 2 ( t-τ )左移到-∞处。然后增加 t ,使 x 2 ( t-τ )逐渐右移。每移到一处,便在(-∞,∞)时间范围内对乘积 x 1 ( τ ) x 2 ( t-τ )做一次积分;这个积分值就是在时间点 t 的卷积值。现在假设把 x 2 ( t-τ )右移到使它的信号起始点 x 2 (0)与时间点 t 1 对齐的位置。此时的 x 2 ( t-τ )变成 x 2 ( t 1 -τ ),如图4.4c所示。
当 τ <0时 x 1 ( τ )恒为零以及当 τ > t 1 时 x 2 ( t 1 -τ )恒为零,所以积分区间被缩小到从0~ t 1 的范围。在此范围内,随着 τ 从0增加到 t 1 , x 1 ( τ )从 x 1 (0)向右变化到 x 1 ( t 1 ),而 x 2 ( t 1 -τ )从 x 2 ( t 1 )向右变化到 x 2 (0)。所以,对图4.4c中两个阴影部分之间的乘积做积分,就得到 t = t 1 时的卷积值。图4.4c下面的小圆点就表示此时的卷积值 y ( t 1 )。
从物理单位上讲,如果 x 1 ( τ )以电压V为单位,而 x 2 ( t-τ )由于是系统冲击响应,所以有 t -1 的量纲。乘积项 x 1 ( τ ) x 2 ( t-τ )的单位就是V t -1 。把乘积项 x 1 ( τ ) x 2 ( t-τ )在某个时间范围内做积分,就约去了 t -1 ,还原出电压V的单位,即 y ( t )的单位是V。
卷积的第三步是把从 t =-∞~+∞范围内的全部卷积值 y ( t )连起来,得到完整的 x 1 ( t )与 x 2 ( t )的卷积曲线,这就是图4.4c下面的 y ( t )曲线。这也就是模拟滤波器的输出响应。
如果用数学公式来描述,信号 x 1 ( t )和 x 2 ( t )的卷积 y ( t )可写为
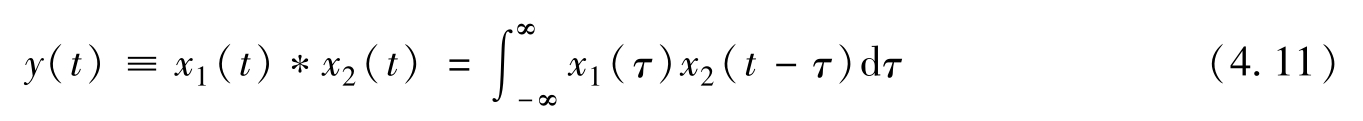
式中,符号“*”表示卷积运算。在上式中,时间变量 t 可看做常量(就像傅里叶变换中的 ω ),而积分变量 τ 在积分完成后随即消失,等式两边只剩下自变量 t 。可以看出,上式与图4.4c是一致的。这是指在式(4.11)和图4.4c中,当计算某个卷积值时, t 是固定的, τ 是变化的,因而 x 1 ( τ )和 x 2 ( t-τ )是反方向行进的。这也就是式(4.11)和图4.4c被叫作卷积的原因。
对于式(4.11),还可以有另一个完全等价的卷积表达式
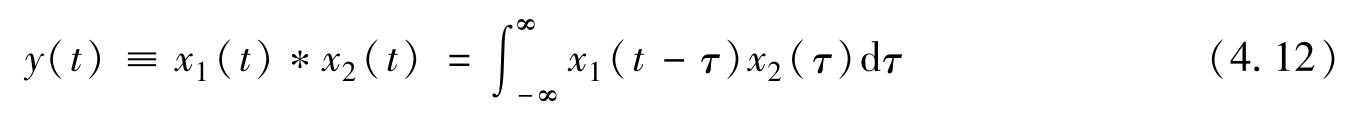
上式对应于把 x 1 ( t )在时间上倒转而使 x 2 ( t )保持不变,这与图4.4中的情况相反。但卷积的结果是一样的。从式(4.11)和式(4.12)可以看出卷积的一个基本特征:被积函数中两个 τ 前面的符号总是一正一负。如果两个 τ 前面都是正号,就变成互相关运算;又如果两个信号是同一个信号,就变成自相关运算了。
最后一点,从图4.4c看,由于 τ 在(-∞,0)区间内使 x 1 ( τ )恒为零,式(4.11)中的积分下限就可以从-∞右移到0。因而,式(4.11)变为
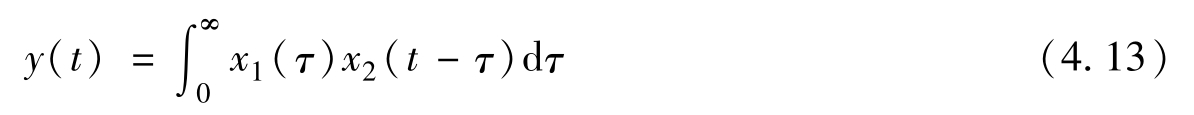
再由于 τ 在( t ,∞)区间内使 x 2 ( t-τ )恒为零,上式中的积分上限就可以从∞左移到 t 。式(4.13)又变为

同理,式(4.12)也可变为
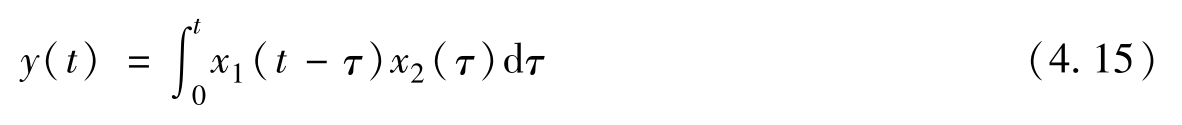
根据式(4.2),写出式(4.13)的拉普拉斯变换式
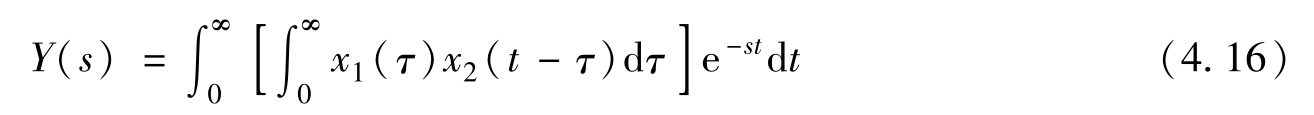
交换式(4.16)中的积分顺序,先做 t 的积分,后做 τ 的积分
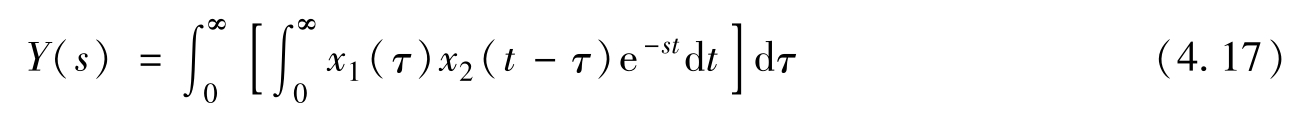
式(4.17)中,由于方括号内以 t 为积分变量,所以 x 1 ( τ )与 t 无关(在做 t 积分时, τ 可看做常数),可以提到方括号之前
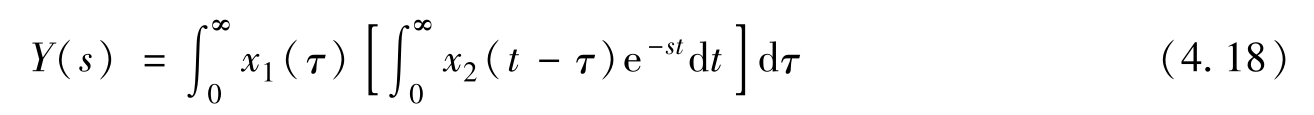
使用变量代换 η = t-τ ,因而 t = η + τ 和d t =d η ,上式可演算为
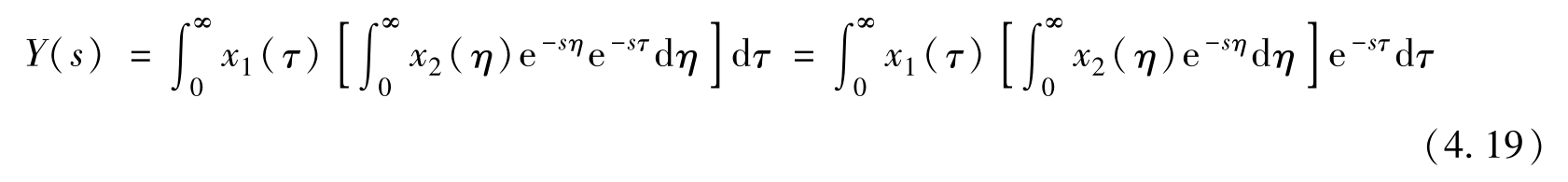
式(4.19)方括号内的就是 x 2 ( η )的拉普拉斯变换,也就是 x 2 ( t )的拉普拉斯变换,上式即可变为
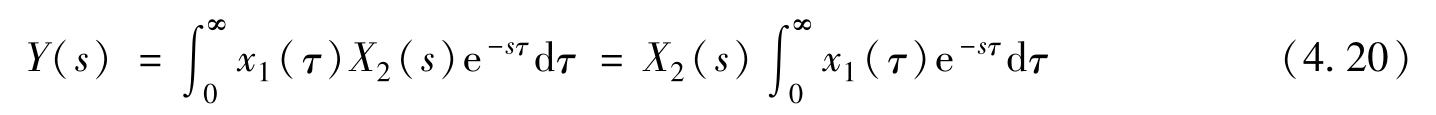
式(4.20)中把 X 2 ( s )提到积分号之前是因为 X 2 ( s )与 τ 无关,而剩下的积分式就是 x 1 ( t )的拉普拉斯变换。所以,式(4.20)就是两个拉普拉斯变换之乘积

式(4.21)就是我们想要的结果:两个时域信号卷积的拉普拉斯变换等于这两个时域信号的拉普拉斯变换的乘积。
小测试
:
两个积分式
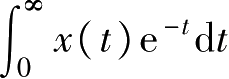 和
和
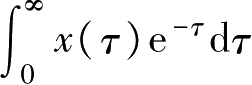 计算的是同一个积分吗?答:是。
计算的是同一个积分吗?答:是。
【 例题4.3 】要求计算连续时域信号 x 1 ( τ )和 x 2 ( τ )的卷积,两个信号的波形如图4.5a所示。
解 :图4.5a中的 x 1 ( τ )可看作系统的输入信号, x 2 ( τ )可看作系统的单位冲击响应,两者的卷积就是系统的输出。连续时域信号的卷积有两个等价的表达式,式(4.11)和式(4.12)。我们使用式(4.11)。这就是,把 x 1 ( τ )固定,而把 x 2 ( τ )在时间上倒转后变成 x 2 ( -τ ),再写成 x 2 ( t-τ ),就可以通过改变 t 使 x 2 ( t-τ )左右平移。令 t =-∞,把 x 2 ( t-τ )左移至-∞;然后增加 t ,使 x 2 ( t-τ )逐渐右移。
从图4.5b看,当 x 2 ( t-τ )右移时,如果 t <0或 t >4,由于 x 1 ( τ )与 x 2 ( t-τ )无重叠部分,卷积值都为零。在0≤ t ≤4的区间内,可分两种情况:0≤ t ≤2和2< t ≤4[这里的 t 与图4.4中的一样,也是指 x 2 ( t-τ )的波形前沿或纵坐标在 y ( t )中的时间值]。
图4.5b表示0≤ t ≤2时的情况。此时, x 1 ( τ )和 x 2 ( t-τ )的重叠面积随 t 的增加而增加,卷积值也随之增加。图中的时间假设为 t = t 1 ,卷积值等于两个阴影部分乘积之积分。由于 x 1 ( τ )恒为1,这个卷积值就等于 x 2 ( t-τ )的阴影面积。这个面积可计算为 x 2 ( t-τ )的高度为1的矩形面积减去上部的倒三角形面积
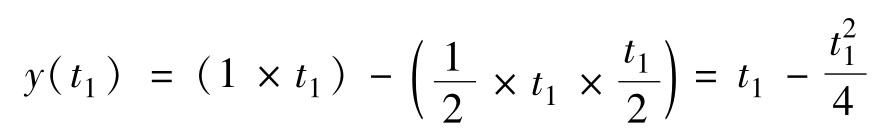
在图4.5b中, t 1 ≈0.5。由上式算出卷积值为 y ( t 1 )≈0.5-(0.5) 2 /4=0.4375,如图4.5b中的下图所示。
把上式中固定的 t 1 改为变化的 t ,就得到0≤ t ≤2区间内的一般表达式
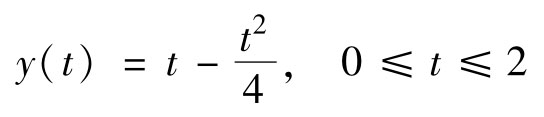
上式表示,卷积在0≤ t ≤2范围内是一条抛物线。将上式对 t 求导,可知当 t =2时卷积达到最大值1。图4.5b最下面的曲线即表示在此范围内的卷积曲线。
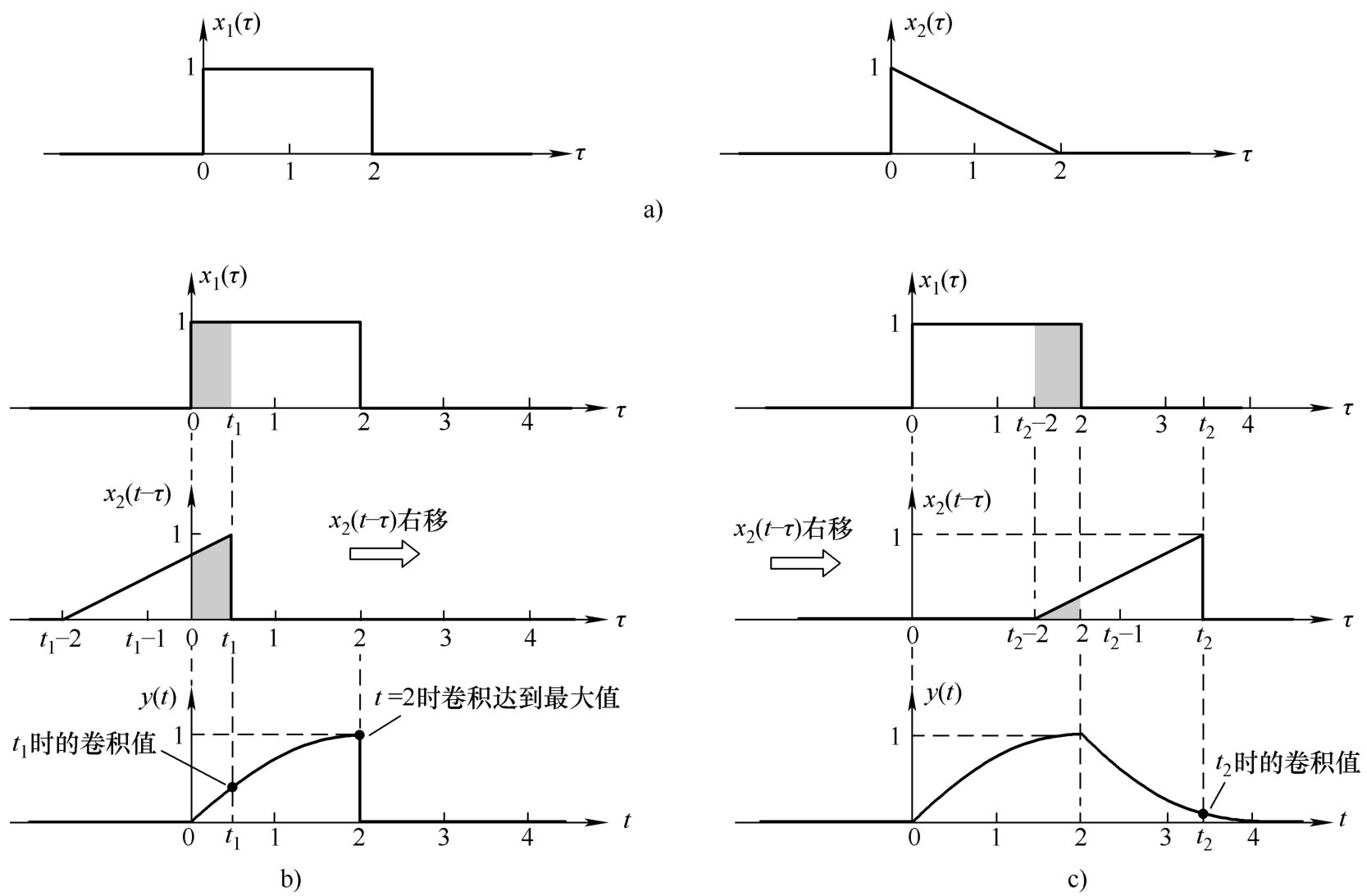
图4.5 两个时域信号的卷积计算
a)两个时域波形 b)当0≤ t ≤2时 c)当2< t ≤4时
图4.5c表示在2< t ≤4区间内的卷积计算。图中,随着 t 的增加, x 1 ( τ )和 x 2 ( t-τ )之间的重叠面积逐渐减少,卷积值也逐渐下降。图中的时间为 t = t 2 ,卷积值等于图中两个阴影部分乘积之积分。由于 x 1 ( τ )恒为1,这个卷积值就是 x 2 ( t-τ )的阴影三角形面积,而三角形的底边长为2-( t 2 -2)=4 -t 2 ,所以三角形面积为
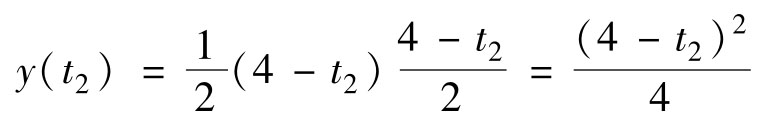
在图4.5c中, t 2 ≈3.4。由上式算得卷积值为 y ( t 2 )≈(4-3.5) 2 /4=0.0625,如图4.5c下图所示。
把上式中固定的 t 2 改为变化的 t ,就得到在2< t ≤4区间内的一般表达式
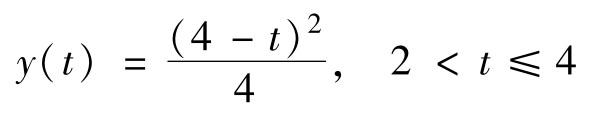
上式表示,在2< t ≤4范围内的卷积同样是一条抛物线。由于 y ( t )是单调降的,所以当 t =2时取得最大值1,当 t =4时取得最小值0。 x 1 ( τ )和 x 2 ( τ )之间完整的卷积曲线 y ( t )示于图4.5c最下面。
举一个非常近似的例子,图中的 x 2 ( t )有点像简单 RC 电路的冲击响应 h ( t ),而矩形的 x 1 ( t )也经常被用作电路的输入信号,作为结果的 y ( t )确实很像 RC 电路在矩形波激励下的输出响应。这也就验证了【例题4.3】卷积计算的正确性。
总结就是,连续时域中实际的滤波操作,是依靠电阻、电容和运算放大器组成的有源滤波器完成的,但从理论上讲,滤波操作是按照卷积的方式进行的。这就是,先用一连串垂线把输入信号分解成许许多多连续的曲边梯形,然后把每个曲边梯形近似为矩形,再利用【例题4.3】中的卷积运算算出每个小矩形的输出响应,把所有的输出响应叠加起来,就得到系统的输出。而做卷积的前提是,系统是线性和时不变的。