




卷积计算的步骤为:先算出理想采样信号 p ( t )的频率谱 P ( f )(上一小节已完成),再假设被采样信号 x ( t )的幅值谱| X ( f )|,最后计算| X ( f )|与 P ( f )之间的卷积。这样得到的卷积曲线就是已采样信号 x S ( t )的幅值谱| X S ( f )|。
为了做卷积,先要改换频率变量名,把 P ( f )和| X ( f )|中的 f 改用其他变量名(比如 ζ ),变成 P ( ζ )和| X ( ζ )|;而把 f 用作由卷积产生的幅值谱| X S ( f )|中的变量名,如图3.12f所示。
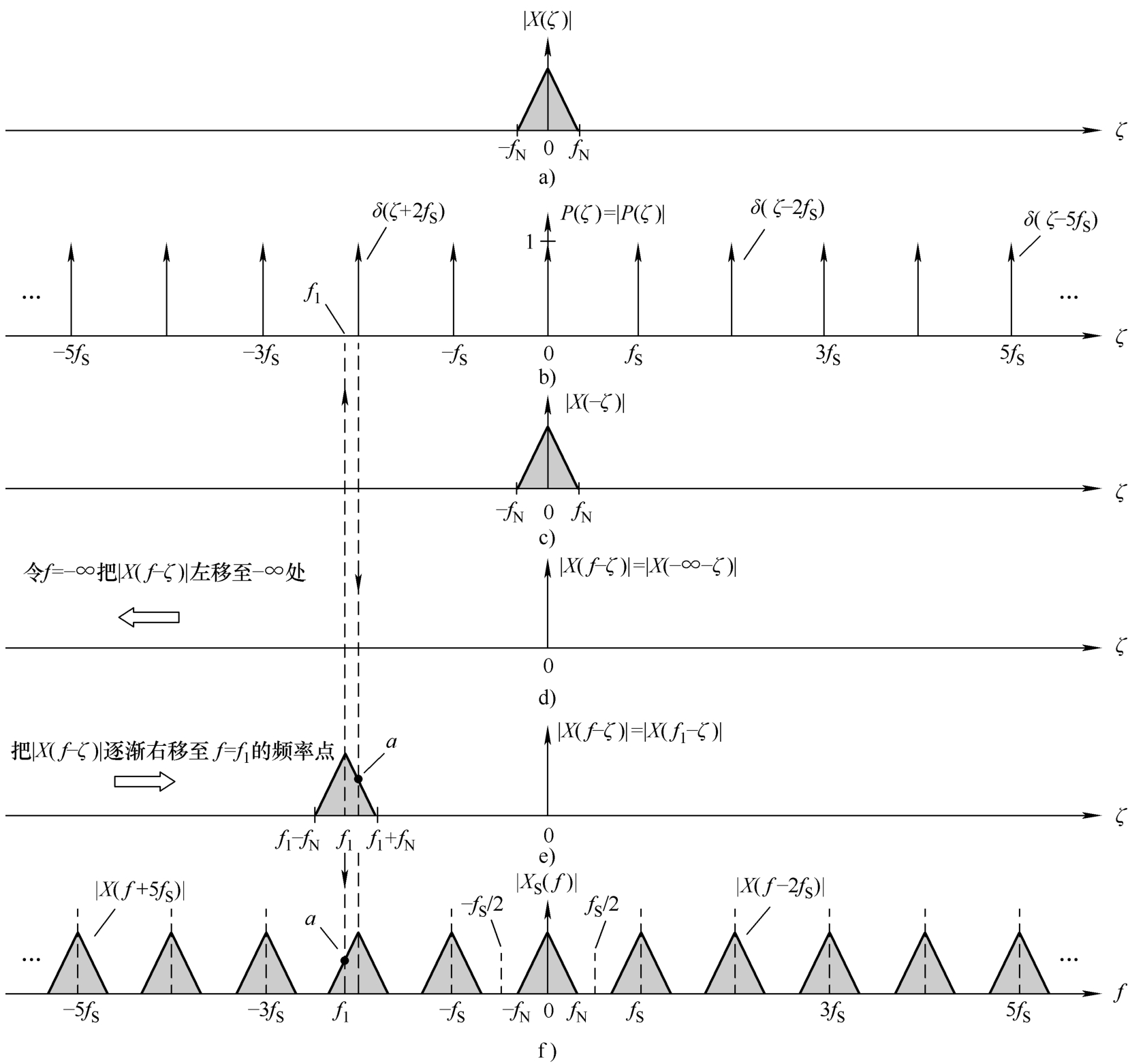
图3.12 |
X
(
ζ
)|与
P
(
ζ
)的卷积
a)幅值谱|
X
(
ζ
)| b)幅值谱
P
(
ζ
) c)把|
X
(
ζ
)|在频率上倒转变成|
X
(
-ζ
)| d)把|
X
(
-ζ
)|改写为|
X
(
f-ζ
)|,再令
f
=-∞,就把|
X
(
f-ζ
)|左移至-∞处 e)增加
f
,使|
X
(
f-ζ
)|从-∞逐渐右移至
f
=
f
1
f)卷积曲线
现在把图3.11中理想采样信号的幅值谱 P ( ζ )重复于图3.12b中。图3.12中 P ( ζ )=| P ( ζ )|是因为 P ( ζ )的相位处处为零;把 f 0 改写为 f S ,以及把幅度改写为1[假设图3.9中理想采样信号 p ( t )的幅度从1变成 T ]。图3.12a为假设的被采样信号 x ( t )的幅值谱| X ( ζ )|, f N 为信号 x ( t )的奈奎斯特频率(奈奎斯特频率是指信号中最高频率分量的频率)。
做卷积按照以下5个步骤进行:
1)使| X ( ζ )|和 P ( ζ )中的任意一个,比如 P ( ζ ),固定不变,如图3.12b所示。把另一个幅值谱| X ( ζ )|在频率上倒转,变成| X ( -ζ )|。由于| X ( ζ )|是偶函数,倒转后的曲线形状不变,如图3.12c所示。
2)把图3.12c中频率倒转后的幅值谱| X ( -ζ )|改写为| X ( f-ζ )|,其中的 f 就是图3.12f中卷积曲线的频率变量。这样改写后,只要改变 f 就可以使| X ( f-ζ )|左右平移。在开始做卷积时令 f =-∞,就可把| X ( f-ζ )|左移到-∞处,如图3.12d所示。
3)让 f 逐渐增加,| X ( f-ζ )|就逐渐右移。每移到一个频率点 f ,就对乘积 P ( ζ )| X ( f-ζ )|在整个频率范围内做一次积分。这个积分值就是卷积曲线在频率点 f 的值。
4)令 f = f 1 ,因而| X ( f-ζ )|变成| X ( f 1 -ζ )|,这就得到图3.12e中的情况。此时,| X ( f-ζ )|已被右移到它的纵坐标与图3.12f中的 f 1 对齐的位置[在图3.12e中, f 1 为常量, ζ 为变量。令 ζ = f 1 ,就得到| X ( f 1 -ζ )|=| X (0)|,而| X (0)|就是图3.12a中| X ( ζ )|的中间值]。这就可以对乘积 P ( ζ )| X ( f 1 -ζ )|在(-∞,∞)频率范围内做积分了。这个积分是很容易的,因为 P ( ζ )的无数个 δ 信号中只有 δ ( ζ +2 f S )与| X ( f 1 -ζ )|有交点。这个卷积值也就简单地等于图3.12e中的 a [ δ ( ζ +2 f S )与| X ( f 1 -ζ )|相乘的情况与图3.5中相同,即利用 δ 函数的筛选特性];而 a 就是图3.12f中 f 1 频率点的卷积值(因为图3.12e中 f = f 1 ),即| X S ( f 1 )|= a 。至此就完成了频率点 f 1 处的卷积计算。
5)在| X ( f-ζ )|从 f =-∞变化到+∞的过程中,需计算出所有的卷积值,再把这些卷积值连起来,就得到图3.12f中的卷积曲线| X S ( f )|。
读者可以仿照上面的步骤,自行计算图f中其他频率点上的卷积值。
由于| X ( f )|与 P ( f )之间的卷积是周期性的[因为 P ( f )是周期性的],所以只要算出在[ -f S /2, f S /2]范围内的卷积值,然后将它复制、平移和叠加,也可得到图3.12f中完整的卷积曲线。
现在可以根据图3.12f中的卷积曲线,写出已采样信号 x S ( t )的频率谱表达式

式(3.11)中已把幅值谱| X S ( f )|改成了频率谱 X S ( f )。这是因为 P ( f )的相位处处为零,使卷积的相位与 X ( f )的相位相同(见图3.12e),使 X S ( f )和 X ( f )有相同的相位值。式(3.11)的意思是:由理想采样操作产生的已采样信号 x S ( t )的频率谱 X S ( f ),等于无数个被采样信号 x ( t )的频率谱 X ( f-nf S )的叠加( n =…,-2,-1,0,1,2,…),其中的 nf S 表示每两个相邻频率谱之间都相距 f S 。
小测试 : 计算两个时域信号频率谱之间的卷积,是否只需做一次在(-∞,∞)区间内的积分。答:否。