




究竟什么是数字?我们之前回避了这个问题,但如果我们接触到更复杂的数字,这个问题就不那么容易回避了。我们经历了一个极其复杂的过程才说清楚整数的概念,包括负数,但我们毕竟做到了。如果再前进一步,阐明分数的概念恐怕会更复杂,它也被称为“有理数”,因为它代表了一种比例关系。但与此截然不同的是所谓的“无理数”。对于这类数字,实际上不难说出它们在世界上描述了什么,但很难把它们构建成一个数学世界。在面对整数的时候,我们认为数字1是基本构成要素,并以此来构建整个世界。那么对于无理数,它的基本构成要素是什么就很难讲清楚了。
你可能已经不记得什么是无理数了,所以我本应告诉你它的定义,但问题就在于很难描述它的定义。有时候无理数被定义为“无限不循环小数”,但这究竟是什么意思?如果一个小数以不循环的方式无限延续,我们怎么知道它是什么样子?无论我们列举出多少小数位,都可能漏掉一些(实际是无穷多)小数位,而我们又无法以某种标准的模式来描述它们,因为它们的特点是永不重复,没有模式可言。
这时候你可能再一次感到费解、困惑、眩晕、不知所措,这些都是经常出现的数学直觉。所谓的“数学高手”对这类问题往往面不改色,从容应对,让那些困惑不已的人觉得自己像个“数学废柴”。事实并非如此,如果有些人欣然地接受了这些概念,那就说明他们必然遗漏了某些细节。
无理数的故事可以追溯到很久以前,它们的出现甚至早于数学家找到理解它们的有效方法。古希腊的数学家已经发现某些东西无法用分数来表示,找到这样一个“数字”并不难(难的是如何证明它不是分数),例如下面这个正方形:
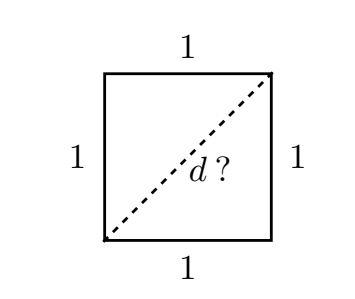
这个正方形的边长为1。你可能会问长度的单位是什么,但抽象数学的美妙之处就在于,长度单位并不重要。1就是一个长度,仅此而已,既然不重要,我也就不做说明了。
现在,我们来看看这个正方形的对角线长度是多少。(你或许又搞不懂我们为什么要操心它的对角线,我只能说这也是一种数学冲动。)如果你还记得毕达哥拉斯,你就能把这个数字计算出来:毕达哥拉斯定理说,一个直角三角形“两条短边的平方和等于长边的平方”。这个定理可以简洁地表述为(又是字母!):
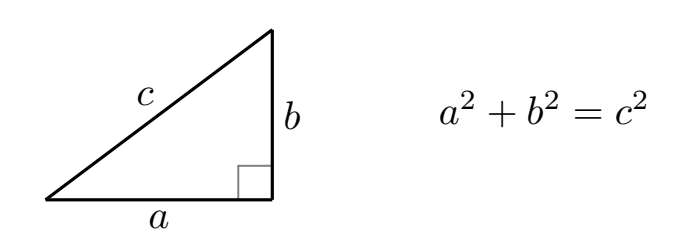
于是我们可以把这个定理套用到正方形中的一个三角形上:如果对角线的长度是 d (字母又出现了),那么它的公式就是:
1 2 +1 2 = d 2
这告诉我们:
2= d 2
它表示, d 是一个平方数为2的数字。然而,我们有可能发现,没有任何一个分数 d 能满足这个条件。这意味着我们只有两种选择:正方形的对角线是一个无法测量的长度,抑或必然存在一种无法用分数来表示的数字。
第一个选择从逻辑上讲并不意味着末日降临,只是让人感受到一丝局限,不那么令人满意。怎么会出现一个没有长度的线段呢?良好的数学直觉让我们察觉到怪异之处。如果我们只允许数字包含分数,那么分数之间就会出现没有数字的微小空白地带。我们可以在空白处放上一个分数,但如果放大来看,空白依然存在。就像我们尽量放大计算机显示器的曲面屏幕,最终只会看到单个的像素一样。
如果数字之间存在空白,那就说明在成长的过程中会有那么一刻我们没有身高数值,这真是太匪夷所思了。因此另一个选择就是,允许一类崭新的数字走进你的生活。
你当然可以决定不让某些东西走进你的生活,很多人就顽固地拒绝接受新事物(比如同性婚姻、非二元性别,或者女数学家),但数学不是这样的(遗憾的是,有些数学家就是这么想的)。数学并非一成不变的僵化知识结构,它总是想接纳新事物。它不一定会让更多的事物进入某些特定的领域,但总是乐于研究一个新的世界,观察新事物如何与旧事物和谐共存。
因此,数学对正方形的对角线显然采取了一种包容的态度,它绝非没有长度,所以必然存在一种分数以外的数字。接下来的问题就是:如果它们不是分数,那么它们是什么?
1872年,数学家格奥尔格·康托尔和理查德·戴德金(分别)在思考该如何用严谨的方式向学生们传授数字的概念。我想象中的场景是这样:就像所有优秀的教师所做的那样,他们在备课时也会猜想学生们的反应,想着如何引起他们的共鸣,并为学生们有可能提出的各类问题准备好答案。这样做能促使优秀的教师更深入地理解授课内容,因为学生有可能从各个角度提出问题,你自己必须从各个角度理解相关知识点。康托尔和戴德金都发现,数学家构建的数字系统并不严谨,于是他们开始动手填补空白。
人类与生俱来的好奇心推动着他们在同一时间开始研究这个课题,但方法截然不同。如果不介绍大量的技术背景,二人的研究方法就很难被解释清楚,但我尽量说明他们的思路。康托尔的想法更像“无限不循环小数”,他借用另一位伟大数学家奥古斯丁·路易斯·柯西的思想,找到了一个精确描述这类小数的方法。因此他的结论通常被称为“柯西实数”,尽管这有些令人费解,但仍值得人们尊敬。戴德金的想法更像找出所有切蛋糕的方式,而不是试图拾起所有的碎屑。如果你找到了所有的切蛋糕的方式,你实际上就已经间接地找到了所有的碎屑。两种思路都为我们提供了填补分数之间的空白的方法,从而构建了一个严谨的数字结构。
然而,我在这里并不是要解释康托尔和戴德金的“实数”结构,也就是包含了无理数的数字体系,我只是想说明,只有深入理解某些事物,才能将其更好地传授给他人,这也是推动数学研究持续发展的因素之一。康托尔和戴德金为精确定义实数概念所做出的贡献,推动了整个微积分领域的发展,而这反过来又使当代世界的所有发展得以实现。这一切都来自两名担心不能回答学生提问的教授。