沿螺旋楼梯继续前进

我们已经用数字相乘的方法研究了图形，但是另一种与数字不那么相关的研究方法就是“对称”。图形比数字更加复杂，而对称就是其复杂性的表现之一。

例如，正方形与长方形既有相似之处又有差异，而它们的差异之一就是对称性。

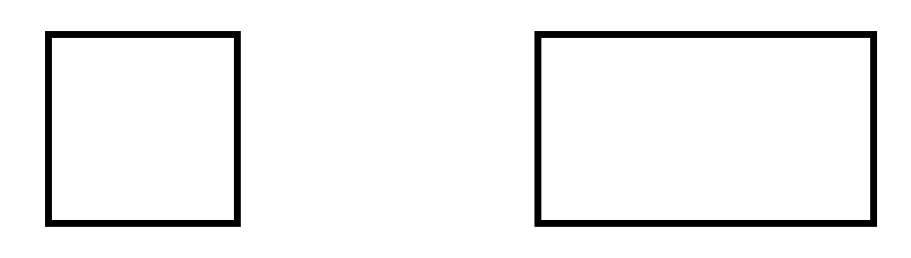
正方形比长方形更对称，如果我们沿对角线将正方形对折，两边的形状完全吻合，但一般意义上的长方形不是这样的。 其实利用这一点，我们能在一张长方形的纸上不借助尺子折出一个正方形：把长方形的一个角沿下图所示对角线对折，我就利用正方形的对称性原理制作出一个正方形。

我们还可以深入探讨，把其他对称类型也包括进来。“折叠型”对称被称为“反射对称”，因为它有点儿像一面镜子映射出图形的一部分。另一种类型的对称看起来像一个风车，图形在旋转过程中某个部分与自身重合，被称为“旋转对称”。

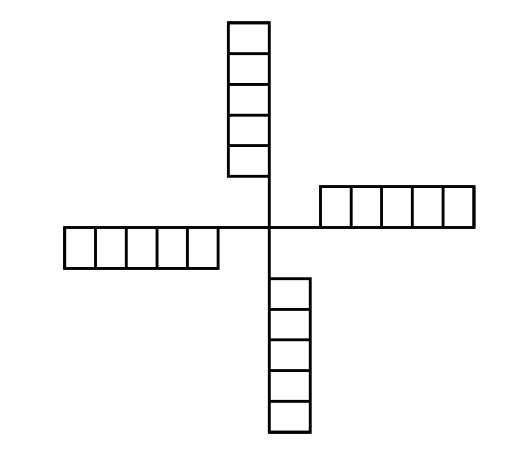
正方形与长方形兼具两种对称特征，我们甚至可以思考如何将各类对称进行组合。这就引出了“群论”的话题，群论就是从对称性中提炼出抽象化的结构，研究它们是如何组合的。从这里开始，我们意识到还有一些与对称相关的问题值得研究，但不涉及图形，让我们有机会再踏上一级螺旋楼梯。其中一个例子是文字对称，也就是所谓的“回文”，比如：

Madam, I’m Adam（夫人，我是亚当）

A man, a plan, a canal, Panama（一个人，一个计划，一条运河，巴拿马）

Taco cat（玉米卷猫）

我们很容易就能看出，这些语句从前往后阅读与从后往前阅读的内容完全一样，当然需要适当忽略空格和标点符号。方程式中也存在对称现象，例如下面这个表达式：

a ² + ab + b ²

a 和 b 扮演的角色完全相同，也就是说，我们如果交换表达式中 a 和 b 的位置，就得到了：

b ² + ba + a ²

这与第一个表达式相同（前提是承认加法和乘法的交换律）。这是另一种类型的对称，其专业研究领域被称为伽罗瓦论。现在我们已经把包含字母的表达式引入了数学研究。（如果字母让你感到紧张，我深表同情，我们在后面的章节会详细讨论字母的问题。）

我们接下来还可以用更多的方法思考带有字母的表达式，比如深入研究它们与图形之间可能存在的某种关系。这样看来，我们先研究了图形和带有字母的表达式，现在开始思考二者之间的关系，这其实就是我的专业研究领域——“范畴论”。这门学科主要关注事物之间的关系，近乎无限地推进这个概念，进而让我们有机会研究几乎所有事物之间的关系。而且，为了以某种相似的方式进行研究，我们还把事物视为“关系”的存在，尽管它们最初并不是某种关系。例如，我们可以把对称视为物体与自身之间的关系，这听起来有点儿古怪，但的确是一项让人受益良多的思维训练。

于是这里就出现了一个关键的概念：既然数学起源于抽象，那么如果找到新的抽象化手段，我们就可以利用数学研究更多的东西，这将为我们的类比研究工作带来浩如烟海的实例。这样的研究方式绝无仅有。如果研究海豚，我们恐怕不能把其他东西想象成海豚，并把它当成海豚来研究。但是对于关系这类抽象的概念，我们完全可以这样做。我们可以把对称视为物体与自身之间的关系。我们可以把火车之旅视为始发地与目的地之间的关系。我们可以把数字视为其他数字之间的关系，比如3是5和2之间的关系，因为它是二者之差。

从这个意义上讲，数学就是寻找灵活思考方式的思维训练，以便在貌似无关的事物之间建立起联系。活跃的思维和创造性的想象力能让这样的关系尽快浮现出来。 tLm29sIZTVtvmmx3afvgaKn18eWHbULNQaK3au+vIdfFl7zREodA2p4b1DeCaCaQ