




就四色命题来说,不同的解读,其破解的思路和证明方法也不同。有比较才有鉴别。本人的证明方法与其他证明方法,究竟哪一种证明方法才是破解四色命题的正确方法呢?不妨通过比较来鉴别。
本人遵循“为什么能够做到”的思路,应用“同中求同,同中求异,异中求异,异中求同”的证明方法求得:一字状结构的图,不论其图的面的数量是多少,仅需 2 色区分,是在于其图的相邻面的组合力为
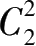 ;梳子状结构的图,不论其图的面的数量是多少,仅需 3 色区分,是在于其图的相邻面的组合力为
;梳子状结构的图,不论其图的面的数量是多少,仅需 3 色区分,是在于其图的相邻面的组合力为
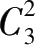 ;梯子状结构的图,不论其图的面的数量是多少,仅需 4 色区分,是在于其图的相邻面的组合力为
;梯子状结构的图,不论其图的面的数量是多少,仅需 4 色区分,是在于其图的相邻面的组合力为
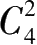 ,并进而求得“图的相邻面的组合力
,并进而求得“图的相邻面的组合力
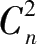 的
n
”与“图的着色种数
S
”具有等于关系。那么,依照“能否做到”论者的穷举法求证,则是,一字状结构的图,当其图的面的数量为 3、4、5……
n
个时,能否做到 2 色区分;梳子状结构的图,当其图的面的数量为 4、5、6……
n
个时,能否做到 3 色区分;梯子状结构的图,当其图的面的数量为 5、6、7……
n
个时,能否做到 4 色区分。无疑,其证明结果只能是对“能否做到”的回答,但对于“为什么能够做到”永远不会有正确答案,也不可能求得“
的
n
”与“图的着色种数
S
”具有等于关系。那么,依照“能否做到”论者的穷举法求证,则是,一字状结构的图,当其图的面的数量为 3、4、5……
n
个时,能否做到 2 色区分;梳子状结构的图,当其图的面的数量为 4、5、6……
n
个时,能否做到 3 色区分;梯子状结构的图,当其图的面的数量为 5、6、7……
n
个时,能否做到 4 色区分。无疑,其证明结果只能是对“能否做到”的回答,但对于“为什么能够做到”永远不会有正确答案,也不可能求得“
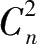 的
n
=
S
”这种关系等式。
的
n
=
S
”这种关系等式。
同样,本人应用比较法和归纳法求得,平、球体表面的图不论其图的面的数量是多少,仅需 4 色区分,是在于其物体表面的全相邻力
L
=4,其图的相邻面的组合力为
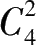 ;环体表面的图不论其图的面的数量是多少,仅需 5 色区分,是在于其物体表面的全相邻力
L
=5,其图的相邻面的组合力为
;环体表面的图不论其图的面的数量是多少,仅需 5 色区分,是在于其物体表面的全相邻力
L
=5,其图的相邻面的组合力为
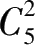 丁环体表面的图不论其图的面的数量是多少,仅需 6 色区分,是在于其物体表面的全相邻力
L
=6,其图的相邻面的组合力为
丁环体表面的图不论其图的面的数量是多少,仅需 6 色区分,是在于其物体表面的全相邻力
L
=6,其图的相邻面的组合力为
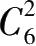 ,并进而求得“物体表面的全相邻力”(
L
)、“物体表面的图的最高相邻面的组合力”(
,并进而求得“物体表面的全相邻力”(
L
)、“物体表面的图的最高相邻面的组合力”(
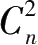 )、“物体表面的图仅需着色种数”(
S
)三者关系的定理为:
L
=
)、“物体表面的图仅需着色种数”(
S
)三者关系的定理为:
L
=
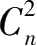 的
n
=
S
。那么,依照“能否做到”论者的穷举法求证,则是,平、球体表面的图,当其图的面的数量为5、6、7……
n
个,又图的面与面之间关系发生变化时,能否做到 4 色区分;环体表面的图,当其图的面的数量为 6、7、8……
n
个,又图的面与面之间关系发生变化时,能否做到 5 色区分;丁环体表面的图,当其图的面的数量为7、8、9……
n
个,又图的面与面之间关系发生变化时,能否做到 6 色区分。无疑,这得借用机器来证明,其证明结果只能是对“能否做到”的回答,但对于“为什么能够做到”永远不会有正确答案,更不可能通过对各物体表面的图仅需着色种数的同异原因而求得“
L
=
的
n
=
S
。那么,依照“能否做到”论者的穷举法求证,则是,平、球体表面的图,当其图的面的数量为5、6、7……
n
个,又图的面与面之间关系发生变化时,能否做到 4 色区分;环体表面的图,当其图的面的数量为 6、7、8……
n
个,又图的面与面之间关系发生变化时,能否做到 5 色区分;丁环体表面的图,当其图的面的数量为7、8、9……
n
个,又图的面与面之间关系发生变化时,能否做到 6 色区分。无疑,这得借用机器来证明,其证明结果只能是对“能否做到”的回答,但对于“为什么能够做到”永远不会有正确答案,更不可能通过对各物体表面的图仅需着色种数的同异原因而求得“
L
=
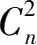 的
n
=
S
”的定理。
的
n
=
S
”的定理。
本人以图的形成原理为切入点,求证到图的面与面之间的相邻关系和非相邻关系均为
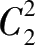 组合关系,图的结构模式是
组合关系,图的结构模式是
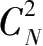 组合模式。“两顶连线”的证明方法是数学界认可的证明方法。那么,这两种证明方法哪一种才是四色命题的可靠的证明方法呢?试举例作证明比较。
组合模式。“两顶连线”的证明方法是数学界认可的证明方法。那么,这两种证明方法哪一种才是四色命题的可靠的证明方法呢?试举例作证明比较。
如图 1、图 2,是我国高等院校“图论”教材中有关“着色理论”的两个例图。图 1 是图 2 “加上新边
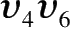 ,
,
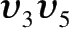 ,
,
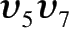 得到的图”,该书以此证明并得出结论:“添加上新边只能色数不减,甚至变大。”
得到的图”,该书以此证明并得出结论:“添加上新边只能色数不减,甚至变大。”
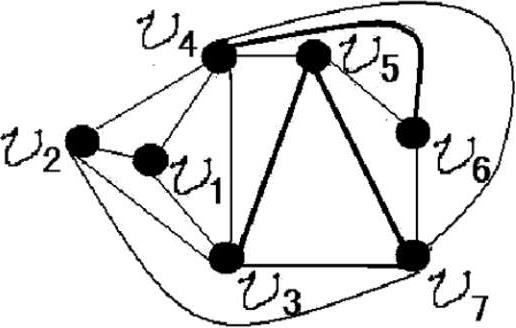
图1
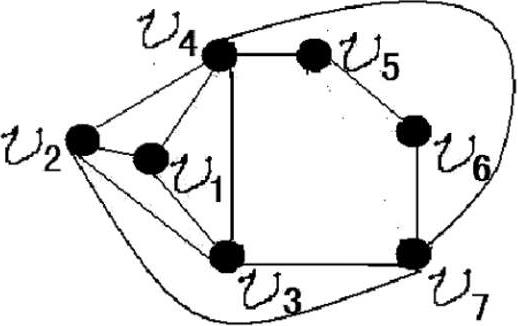
图2
图 3 是应用“组合说”证明方法将图 1、图 2 完整表达后的图表。
从图 1、图 2 与图 3 的比较中可知,“两顶连线”的证明方法对“添加上新边只能色数不减,甚至变大”的结果未能说出其“所以然”,而“组合说”证明方法对此结果能说出其“所以然”:图 1 “添加上新边”后,虽是相邻点(即边)增加了,但其图的相邻面的组合力并没有升降,仍为
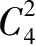 ,故色数仍为 4。
,故色数仍为 4。
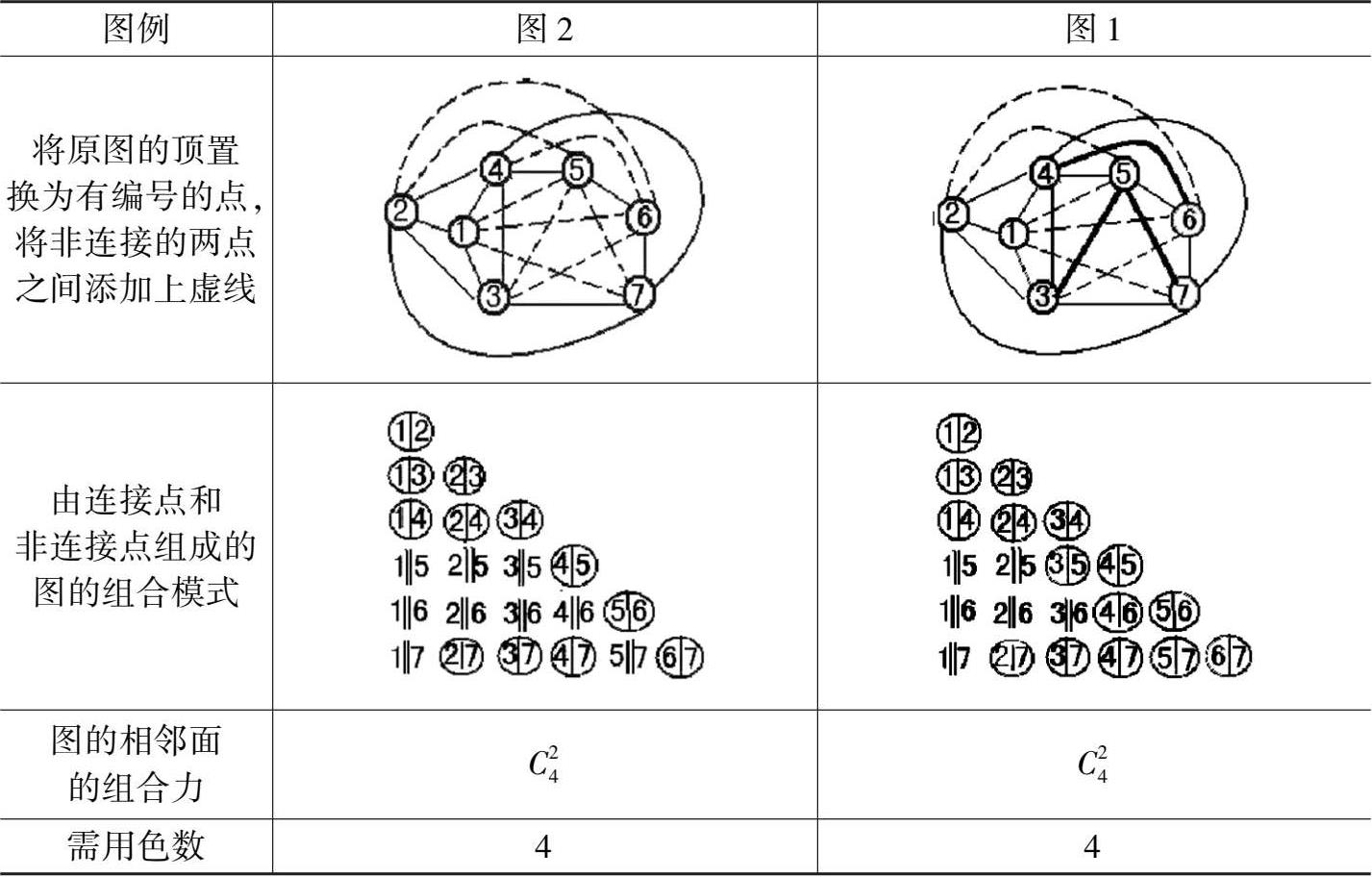
图3 图 1、图 2 完整表达证明图
坦诚地说,这不能说“两顶连线”的证明方法是错误的证明方法,而问题是在于人们应用此证明方法时存在欠缺的地方:其一,图中表达的内容欠完整,只表达“两两相邻”关系,不表达“两两非相邻”关系。这只能说是“半个图”;其二,证明的程序欠完整,将面置换为顶(或点)、添加上连接线后,就直接进入证明程序,漏缺了将“两两相邻”关系和“两两非相邻”关系以组合数字完整记录下来,并循序对号入座到组合模式中去这个程序。正因为如此,不可能证明到图的结构模式是
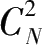 组合模式,更谈不上从图的
组合模式,更谈不上从图的
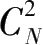 组合模式中发现更多的东西。诚然,在应用“两顶连线”的证明方法时,假如表达的内容和证明的程序都是完整的(见图 3),那么,其证明结果与本人证明方法的证明结果则必是殊途同归。正因为表达内容欠完整和漏缺了必要的程序,致使应用“两顶连线”的证明方法对地图着色区分(即四色猜想)的证明,乃是应用拓扑原理创造出新的假象(即平面图着色区分)来证明原来的假象(即地图着色区分)的证明而已。
组合模式中发现更多的东西。诚然,在应用“两顶连线”的证明方法时,假如表达的内容和证明的程序都是完整的(见图 3),那么,其证明结果与本人证明方法的证明结果则必是殊途同归。正因为表达内容欠完整和漏缺了必要的程序,致使应用“两顶连线”的证明方法对地图着色区分(即四色猜想)的证明,乃是应用拓扑原理创造出新的假象(即平面图着色区分)来证明原来的假象(即地图着色区分)的证明而已。
图 4 是 K 5 图,即是五色区分图。无疑,如按图 4 所表达的那样,图中的10 条线均为连接线,表明 5 个点全连接,需 5 色区分。但如将它展现在平体表面,是不可能实现的图(地图)。因为,事实证明,平体表面不能做到五个点(面)全连接。
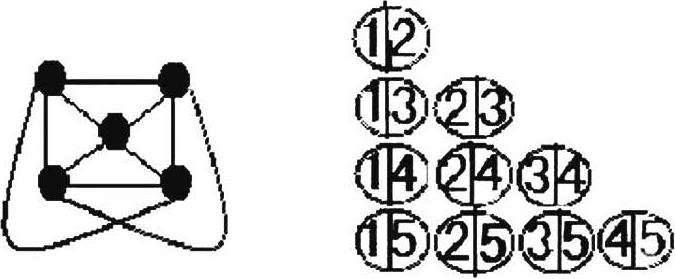
图4 及其组合模式
图 5 是本人对平体表面不能做到五个点全连接的证明图。图中的实线是表示连接线,虚线是表示非连接线。因①与⑤两个点的连线是非连接线,故图中五个点不能做到全连接,图的相邻面组合力为
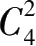 ,需 4 色区分。
,需 4 色区分。
图 4、图 5 两个图同为由 5 个点 10条线组成,所不同的,图 4 的 10 条线均为实线,图 5 的 10 条线为 9 条实线、1 条虚线。这“1 条虚线”之差,就是本人的“组合说”证明方法与“两顶连线”的证明方法的本质区别。那么,这两个图谁的表达是正确的呢?笔者提供两个实例作为检验的参考标准。
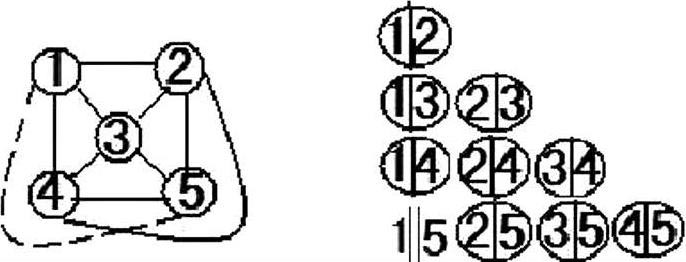
图5 及其组合模式
实例 1 有 5 个城市彼此交通直达。现以 5 个点表示 5 个城市,以实线表示交通线(或公路),用图表达出来。可以肯定,图中 10 条线必有两条线交叉通过,亦即必有 1 条交通线被另 1 条交通线隔断。
实例 2 将 K 5 图的 5 个点置换为 5 个面(即区域),可以肯定,不论如何变换此 5 个面的面与面之间的关系,必有两个面非相邻。
笔者对“两点(顶)连线”的证明方法确立了这个规则:连接线与连接线不可交叉通过;非连接线与非连接线可交叉通过;非连接线与连接线可交叉通过。当你对两个实例得出“肯定”的答案后,你认为这个规则是不是必须遵循呢?
在这里,我想说句真话:“请不要戴着‘图论’的有色眼镜、而要以平等的眼光来看本人的证明方法及学术论文,正确比规范更重要。”
科学发展史告诉我们:只有后人发现、纠正前人的错误理论,不可能前人发现、纠正后人的错误理论。但是,前人的错误理论尤其是被公认为正确的错误理论,往往容易引领着后人往错误的方向走下去。在四色猜想命题的研究上,是不是被一种被公认为正确的前人的错误理论引领着?——这正是我怀疑的,也是值得大家思考的。
2010年8月18日(完稿)
(本文发表于《科技创新导报》2011年第1期)