




思维是人脑对客观事物的本质及其内在规律性联系概括的和间接的反映。数学思维是人脑和数学对象交互作用并按照一般的思维规律认识数学本质和规律的理性活动。具体来说,数学思维就是以数和形及其结构关系为思维对象,以数学语言和符号为思维的载体,并以认识发现数学规律为目的的一种思维。数学思维可以分为逻辑思维、形象思维和直觉思维。其中形象思维是依托形象材料,对事物作出理解的思维。它的基本形式包括表象、直感和想象。它的主要心理成分有联想、表象、想象和情感。
形象思维对于人类的发明创造有着重要的意义。人类发现,掌握事物的本质,人类科学技术发明,首先是从形象思维开始的。如我国古代发明家鲁班,因为手被有带齿的小草刺破而发明了锯子;牛顿看到苹果从树上掉下来,发现了万有引力;著名科学家瓦特看到水壶里水开了,蒸气能掀动水壶的盖,从而发明了蒸汽机……所有这些都说明,形象思维实质上是人们对日常生活中的事物和现象的直观感觉的应用,这种直觉以表象为基础,进行联想与想象,达到创造发明的目的。我国著名科学家钱学森曾经说:“我建议把形象思维作为思维科学的突破口……这将把我们智力开发大大向前推进一步。”
形象思维对于学生的数学学习有着重要的价值取向。在小学阶段,儿童的思维的特征主要是从具体形象思维向抽象逻辑思维过渡和发展的,这阶段儿童的思维以具体形象思维为主。小学低年级,虽然在思维中已经有了抽象的成分,但主要仍是以具体形象思维为主。即使到了高年级,他们的抽象思维仍然占有很大的具体形象性,抽象的过程仍然需要感性材料的支持。因此,培养学生的形象思维能力,既是儿童本身的需要,又是他们学习抽象数学知识的需要。感性知识和经验是学生理解、掌握知识的支柱。发展学生的思维,首先要从发展学生的形象思维着手,并在此基础上,加以概括,引发学生的抽象思维。
数学形象思维有如下的功能:第一,数学形象思维以形象的形式反映数学规律,从而提供数学问题生动而形象的整体显示。因此,易于把握整体。第二,数学创造性往往从形象思维中受到启发并以形象思维为先导。从古到今,形象思维给数学猜想、数学方法的提出以及数学创造都带来了活力。第三,数学形象思维可以弥补抽象思维的不足。抽象思维是一种概念的运动,在认识真理方面具有无可怀疑的可感力与优越性。
感知是感觉和知觉的复合概念。感知是思维活动的窗户,是人们深入认识事物本质的开端。小学生认识事物带着很大的具体性和直观形象性,特别需要先从感知窗户里得到一定的感性知识,作为升华到理性的诱因和基础。德国心理学家艾宾浩斯说过:“保持和重现在很大程度上依赖于有关的心理活动第一次出现时注意和兴奋的程度。”这里说的“第一次出现”,指首次感知问题。感知材料所呈现的程序、结构以及刺激物信息程度的强弱,对于能否在大脑中形成准确清晰的表象,具有十分重要的意义。因此,发展学生的形象思维,首先要强化学生的感知。
◇让感知逐步走向深入……(选自苏教版教材二年级(上册)《秒的认识》)
《秒的认识》一课的教学,为了强化 1 秒的第一印象,教者设计了三个层次的教学活动。(1)让学生自主演示 1 秒:让学生先拿出钟表看一看、听一听,再用自己的声音和动作进行演奏。学生一边发出“咔嚓、嗒嗒、嚓嚓”等声音,一边用打节奏、拍手肘、跺脚等方式进行演示,教者适时引导学生评价演示动作的快与慢。在此基础上,要求全体学生跟着课件伴奏进行有声和无声的演奏。(2)体验感知 10 秒:10 秒有多长呢?闭上眼睛静静地听,老师喊开始,当你认为 10秒到了就喊“停”,讨论:你是怎样感受出 10 秒的?(3)估计内化 20、30 秒:教师分别播放 20 秒的铃声和 30 秒的音乐,让学生估计这段时间有多长?说说你是怎样估计的?
感知是学生形象思维的起点。在上述片断中,教者重视 1 秒的首次感知,首先让学生听秒针走动的声音、学秒针走动的节奏。再让学生从“学生独自听”到“听后个体模仿”,从“全班整体演奏”到“个体独立演奏”,从“有声音提示打节奏”到“无声音提示凭感觉打节奏”。这样 1 秒的印象才会深深地刻在学生的脑海里。几秒是 1 秒的积累。让学生估计一段时间有多长,既是对“几秒”的体验,也是对“1 秒”建构的检验。
活动是认识的基础。实践操作是一种特殊的认识活动。一方面,操作活动是手与眼协同活动对客观事物的感知过程。另一方面,操作活动又是手与脑密切沟通,把外部活动系列转化为内部语言形态的智力内化方式。小学生动手操作,总是在视觉与触觉、运动觉协同感知事物的同时,就以内部语言悄悄地展开思维,他们在操作时必须同时思考,如何摆放,如何分拆,如何移动,如何剪拼,如何折叠……而在操作中获得的形象和表象,及时推动着他们进行分析、综合、比较、抽象、概括,更能引起和促进学生把外显的动作过程与内隐的思维活动紧密地结合起来,使之成为“思维的动作”与“动作的思维”。
◇让智慧火花在指尖上跳跃!(选自苏教版四年级(下册)《素数和合数》)
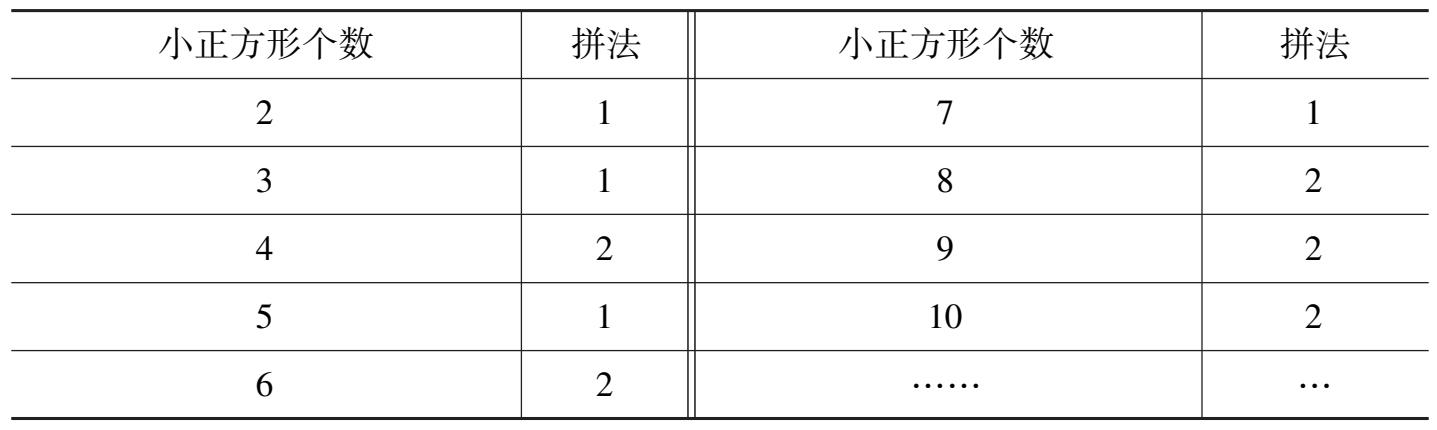
1.用 2、3、4 个相同的小正方形纸片拼成大长方形,说一说各有几种拼法。
2.用 4 个小正方形拼成长方形的个数比用 2 个、3 个小正方形的拼法要多。是不是小正方形的个数越多,拼法也越多?拼一拼,看看这样的猜想是否正确。
3.为什么有的只能拼成 1 种长方形?你发现这类数有什么特点?有的却能拼出 2 种或者 2 种以上的长方形?这类数又有什么特点?
4.总结:长方形拼法的多少与数的因数有关系。揭示:素数和合数的定义。
“学生的智慧在指尖上。”如何引导学生在活动中发现问题,在对问题的解剖中探究知识,生成智慧?而不仅仅是在完成教师的规定“动作”,成为教学中必须思考和解决的问题。这则教学片断作出了较好的诠释,凸现了实践性特点,通过拼玩,学生自己发现问题、分析问题。在拼玩中思考,思考中建构。有效的操作发展了形象思维,推动了抽象逻辑思维的展开。
表象是一种普遍的心理现象,它是以前感知过的事物在头脑中留下的形象。表象是从感知而来的,但比感知更进一步,具有直观形象性和初步概括性双重特点。所谓直观形象性,是指大脑中的那些感知过的事物、事件的形象、情境,就像历历在目那样真切、清晰。所谓初步概括性,是指表象常常综合了多次感知的结果,概括了多次感知的内容,个别事物的特点消失了,留下的是事物的一般特点。表象是直观感知向具体形象思维发展的必不可少的中间环节。没有感知便没有表象,没有表象便没有形象思维的产生,也没有抽象逻辑思维的发展。
◇让表象在经历体验中不断完善(选自苏教版教材二年级(下册)《认识角》)
1.在“摸角”中初步感知
(1)这是三角尺的一个角,如果用手掌心摸一摸这儿(指顶点),会有什么感受?(尖尖有点戳手;揭示:“顶点”)
(2)从顶点分别顺着这两条边摸下去你有什么感受?(揭示:“边”)
(3)指明:角就是由一个顶点和两条边组成的图形。
2.在“画角”中形成表象
出示儿歌:“小小角,真简单;一个顶点两条边。画角时要牢记;先画顶点再画边。”教师示范,让学生伸手书空画角。
3.在“找角”、“做角”中丰富表象
(1)找一找生活中哪些物体的面上有角?出示图形,你能找出其中的角吗?
(2)选用一种或几种材料创造出一个角:①两根小棒;②一根吸管;③一根绳子。
建立表象是学生从形象思维向抽象思维过渡的中介。教者把对角的表象建立在丰富感性材料的基础之上,设计了“摸一摸”“画一画”“找一找”“做一做”等教学活动,从实物中抽象角,从辨析创作中理解角。充分遵循了(从)感知→(建立)表象→(到)概念的认知规律,完成了“物——形”的抽象过渡。表象的内化,有助于学生更快地摆脱具体事物的束缚,促进感性经验向抽象思维转化。
想象是在头脑中对已有表象进行加工、改造、重新组合形成新形象的心理过程。作为一种特殊形式的思维,想象具有形象性、新颖性、创造性和高度概括性等特点。爱因斯坦所说:“想象力比知识更重要,因为知识是有限的,而想象力概括世界的一切,并且是知识进化的源泉,严格地说想象力是科学研究中的实在因素。”课堂教学中的创设问题情境,丰富学生的想象,是提升学生形象思维的一种重要举措。
◇片断一:在想象中感悟“一一间隔”的规律(选自苏教版四年级(上册)“找规律”)
教师引导学生列举生活中的“一一间隔”现象,用符号、字母等表示出“一一间隔”。通过男女生排队的游戏排出“一一间隔”,并记录相关数据。在此基础上,教师要求进行想象练习:
(1)观察这组数据(指男女生“一一间隔”数据),你肯定能悟出究竟什么情况下才能一一间隔?
(2)把这种感觉放在心里,做一组想象练习:下列每组中两种物体能这样“一一间隔”排列吗?
①4 棵柳树、4 棵杨树;②5 朵红花、4 朵蓝花;③4 枝铅笔、7 块橡皮;④100只键盘、101 只鼠标。
(3)讨论并记录,在能够一一间隔的数据后面打√,不能的打×。
◇片断二:在想象中发现长方体“面”的特征(选自苏教版六年级(上册)“长方体正方体的认识”)
(1)(出示长方体直观图)擦去一条棱,你能想象出原来的样子吗?再擦去三条呢?最少保留几条棱?
(2)观察这三条棱有什么特点?揭示:长、宽、高。
(3)根据长、宽、高的数据,你能想象出这个长方体的 6 个面吗?它的 6 个面应该对应下图中的几号图形?
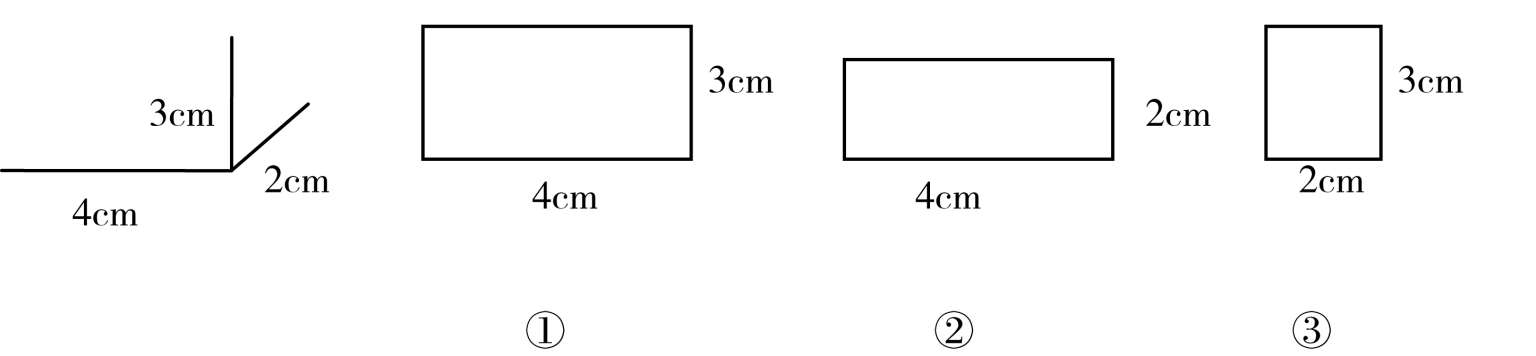
(4)说一说:长方体的“面”有什么特征?
片断一教者在学生充分感知“一一间隔”规律的基础上,通过想象让学生再次感悟“一一间隔”排列,丰富对规律的认识。不仅如此,这种再造性想象,还引导学生把对规律的表面现象的认识,逐步抽象到对数据的关注,为进一步分析数据,探究“一一间隔”的规律打下伏笔。片断二教者没有应用操作的方法让学生探究长方体“面”的特征,而是引导学生通过想象揭示“长、宽、高”的基础上,再展开合理联想,把长方体的 6 个面和对应的长方形连一连。在想象和联想的交融中,引导学生发现长方体“面”的特征,可谓独具匠心。
形象思维是人类思维的一种高级和复杂的形式。学生数学形象思维能力的培养,既是儿童本身的需要,也是他们学习抽象数学知识的需要。培养学生的形象思维能力,是一项长期的任务,作为教师要深入了解形象思维的价值取向,掌握形象思维的方法举措,把形象思维的培养与日常教学相结合,渗透于教学活动的方方面面,发挥形象思维的优势,把学生形象思维的提升与综合素养的提升有机相融。