




数学的基本语言是文字语言、符号语言和图像语言,其中最具数学学科特点的是符号语言,是人们进行计算、推理和解决问题的一种工具。数学符号简洁、抽象、准确、清晰,具有简约思维、提高效率、便于交流的功能。为学生创设学习情境,唤醒生活经验,并在相互交流的过程中,逐渐理解符号的意义,利用符号来解决问题是培养学生符号意识的有效策略。
符号在现实生活中随处可见。道路旁醒目的交通标志、公共场所张贴的提示标志、地图上各种标志等,虽然没有详尽的文字描述,却能让人一目了然,这正是符号的魅力所在。
符号作为数学的语言,作为一种重要的数学工具,在数学学习过程中起着举足轻重的作用。学生的符号意识就是在数学学习过程中自觉养成用符号来表示数、数量关系和变化规律等的习惯,能主动地、普遍地运用符号去描述研究的对象。
《标准》指出:符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性。
符号语言因为其简洁、方便、清晰等优势而成为最具数学学科特点的基本语言。培养学生的符号意识是发展学生思维的需要,是将数学问题抽象化、一般化的需要,更是丰富学生数学素养的需要。
培养学生的符号意识有助于推动数学的发展。系统地运用符号,可以简明地表达数学思想,提炼数学运算或推理结果,通过符号化的方式表示一般化的结论。在一定程度上,将数学问题符号化,能加快数学思维的速度,实现数学抽象化,促进数学认识和数学思想的提升。
我们的生活离不开符号,我们的数学也离不开符号,我们在教学中一定要重视符号意识的培养,来发展学生的数学语言,提高学生的应用能力,拓展学生的创新思维。
数学符号与我们的生活息息相关。从某个意义上来说,我们生活在一个被符号化的世界中,培养学生潜在的“符号意识”,充分利用学生生活中潜藏的“符号意识”,就要给学生提供机会,让学生经历“从具体事物——学生个性化的符号表示——学会数学地表示”这一逐步符号化、形式化的过程。
教师永远是学生学习上的引路人,是数学思想和方法的传递者。教师在教学过程中使用符号的频率,决定着学生符号意识被调动的可能性大小。
课堂教学中,很多规律或公式在呈现时如果用文字表达出来,教师书写比较费时,常常会影响教学时间,但如果在学生讨论交流的基础上,以简洁的符号形式板书出来,并让学生联系自己的理解加以消化吸收,既让学生在认知上实现了一般语言向数学语言的飞跃,也使学生的思维得到了提升,长此以往,教师的这种看似无意识的符号化行为,其实是在不间断地向学生传递符号意识,带领他们感知符号的便捷,初步激发他们心中潜在的符号意识。
数学的产生和发展与现实生活密不可分,在教学过程中,如果能创设具体的问题情境,将会起到事半功倍的效果。
比如在教学“搭配规律”时,课件出示商店柜台里有 3 个穿不同颜色的木偶娃娃,旁边还有两顶不同颜色的帽子。提问:小明打算买一个木偶娃娃,再配上一顶帽子,可以怎样选配呢?学生根据经验,很快想到搭配的方法,并用一般语言表达出来,但通过交流发现在用数学方法表示出来时不够简单,不利于操作,如果要画木偶娃娃和帽子对有些学生来说又有一定的难度,于是学生潜在的符号经验被调动起来,自主思考出了以下策略:
策略一:分别用△和□表示木偶娃娃和帽子,用连线的方式选配;
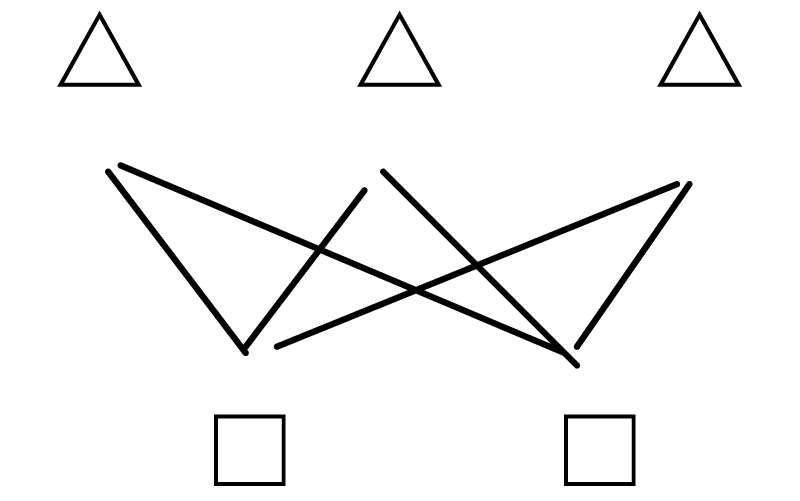
策略二:分别用数字和字母表示木偶娃娃和帽子,搭配后记录下来:
1A、1B、2A、2B、3A、3B;
策略三:用☆和○分别表示木偶娃娃和帽子,记录如下:☆1○1、☆2○1、☆3○1、☆1○2、☆2○2、☆3○3;
在熟悉的生活情境中,学生很快能找到搭配方法,但由于图、文的表述不及符号语言简洁,于是依赖于图文理解,符号表示法应运而生,学生潜在的符号意识被诱发。这些富有个性的符号正是已有的符号意识在起作用,学生惊喜地发现自己也是一个研究者、探索者和发现者!
3.注重激励评价,倡导符号意识
教师的鼓励就像是一剂兴奋剂,能够让学生的思维快速处于亢奋状态,达到最佳效果。教师教学行为中的激励性评价是对学生学习最直接、最有效的促进手段。符号意识的培养和发展不是一朝一夕之事,而应贯穿于数学学习的全过程,伴随着学生数学思维的提高逐步发展。因此,教师的态度尤其重要,肯定和鼓励将对学生的符号意识的产生和发展产生积极的正面效应。
比如:在教学“用字母表示数”时,出示例题:摆一个三角形要 3 根小棒。
(1)按照图中的方式,摆 2 个三角形需要几根小棒?摆 3 个呢?

(2)摆 10 个这样的三角形需要几根小棒?
(3)摆 100 个这样的三角形需要几根小棒?
(4)如果用a表示所摆三角形的个数,那么搭a个这样的三角形需要多少根小棒?与同伴交流。
在摆 2 个、3 个、10 个这样的三角形时,学生可能会根据范例画出相应的图,并数一数小棒的根数,但当摆到 100 个这样的三角形时,学生就开始出现了困难,这时,如果教师不注重言语上的鼓励,对学生中出现的可能不尽善尽美的表示法不予以肯定,学生的探究欲望就会减弱,也就发现不了三角形的个数与小棒的根数之间的关系及小棒根数的变化规律。反之,学生在放松的状态下,思维会更活跃,也就难免不会出现一些精彩的表达式:3 + 2(a -1)、1 + 2a、3a -(a -1),这些表达式都能充分体现三角形的个数与小棒的根数之间的关系及小棒根数的变化规律。