




首先我们介绍秦九韶本人对“三斜求积公式”的证法.
证明1 如图6-1( a ),作高 AD = h ,设 BD = m , DC = n .
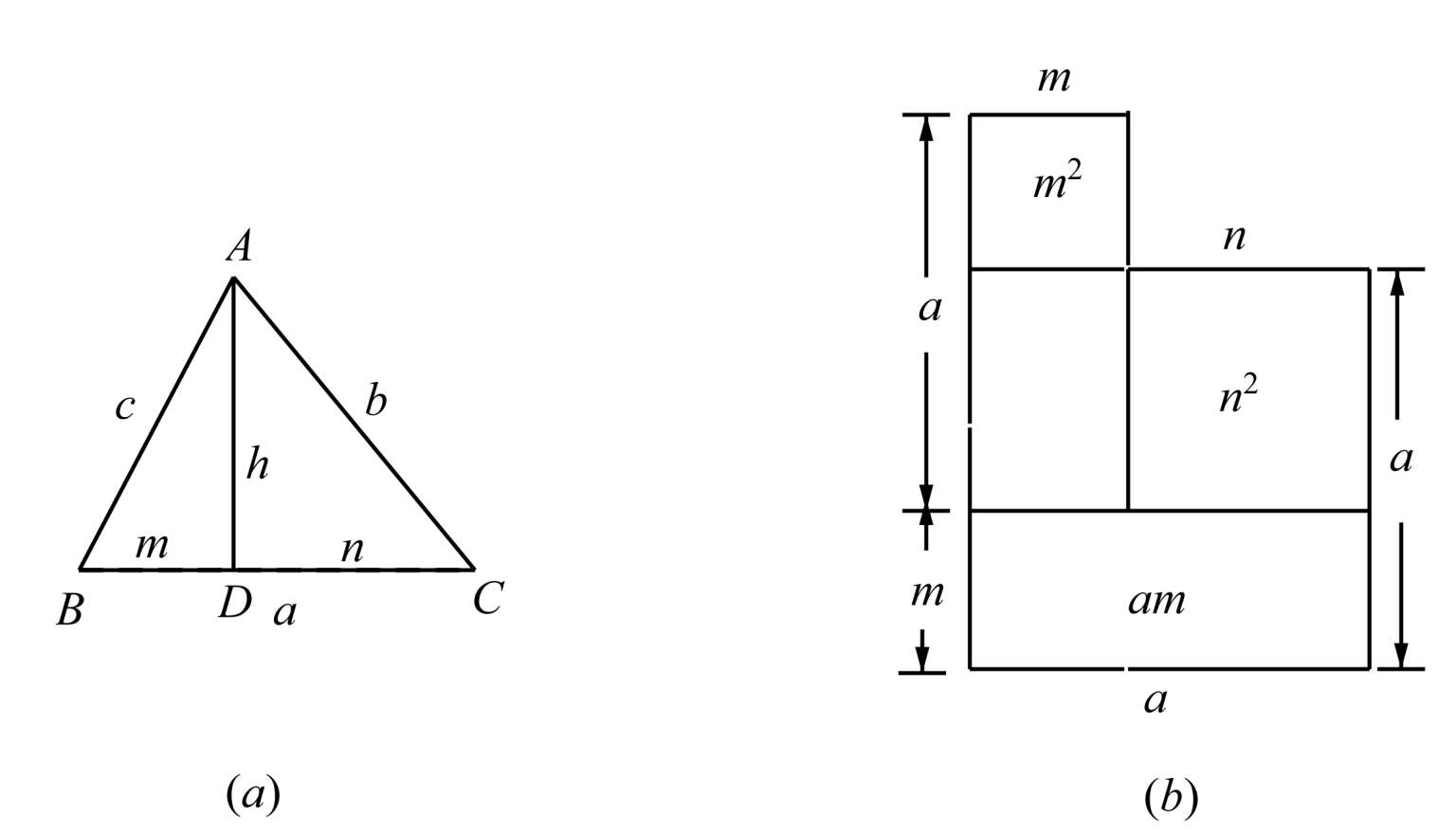
图6-1
由
S
=
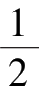 ah
(古代称为圭田求积法)
ah
(古代称为圭田求积法)
自乘得

由勾股定理

将②代入①得
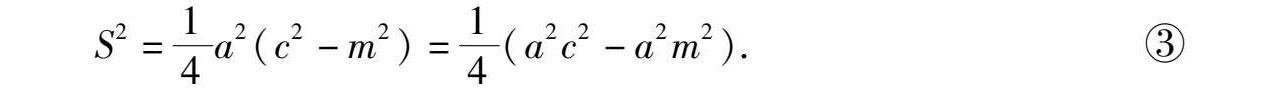
又依②得
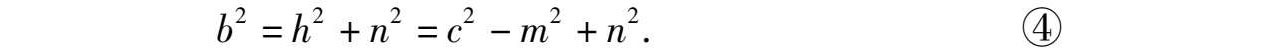
从图6-1( b ),由演段法得知

以⑤代入④得
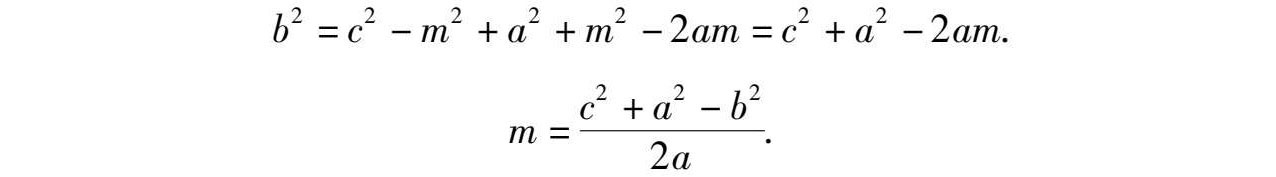
代入③得
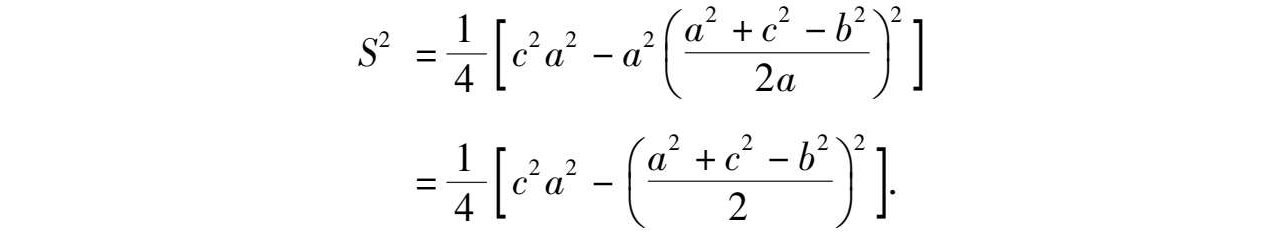
所以
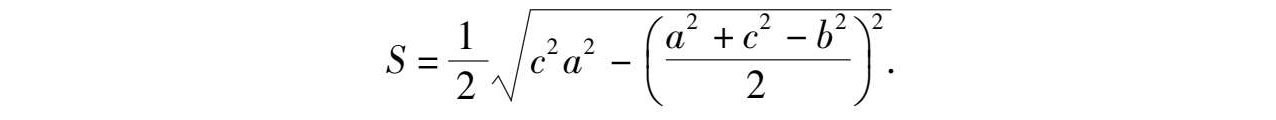
即“三斜求积公式”得证.
下面我们来证明秦九韶-海伦公式.
证法2 同证法1所设,有

⑥-⑦得
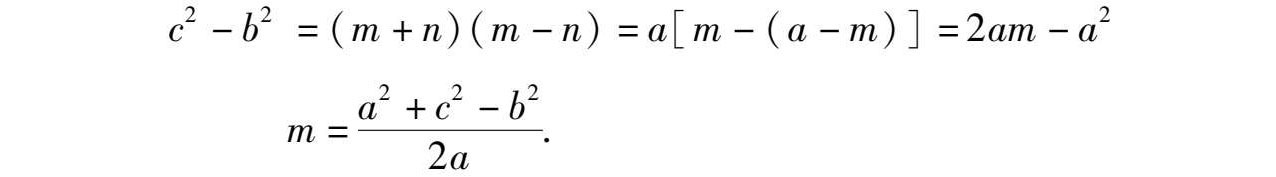
于是有,
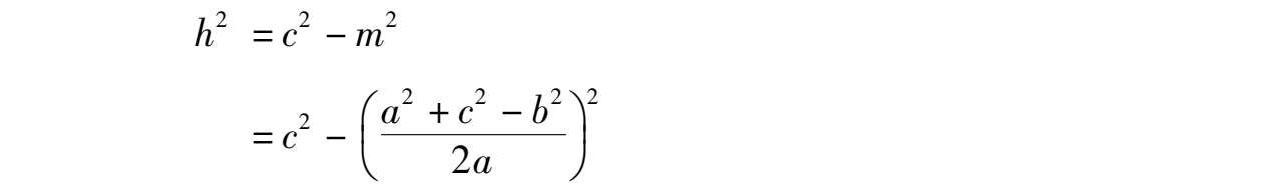
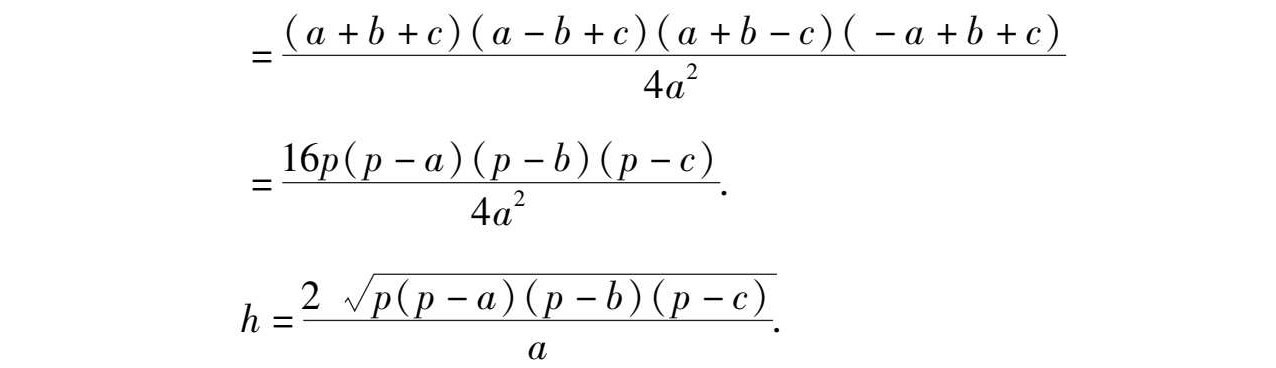
所以
S
=
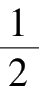 ah
=
ah
=
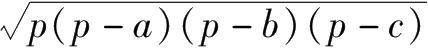 .
.
证法3
因为cos
C
=
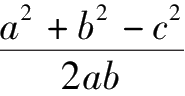 ,
,
所以
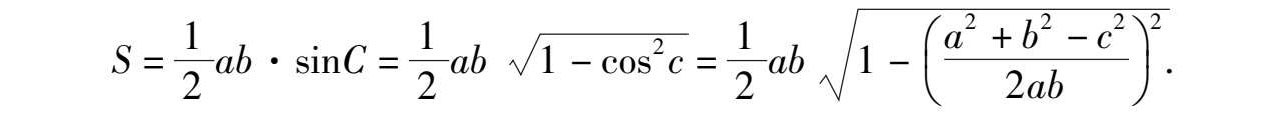
化简整理得
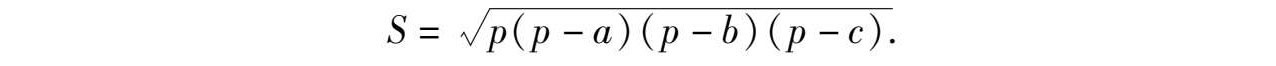
证法4 如图6-2,设 O , O′ 分别为△ ABC 的内心与旁心, r 、 R 是☉ O ,☉ O′ 的半径, D 、 E 是切点,易知 AE = p , AD = p - a , DB = p - b , BE = p - c ,由于∠ OBO′ =90 ° ,
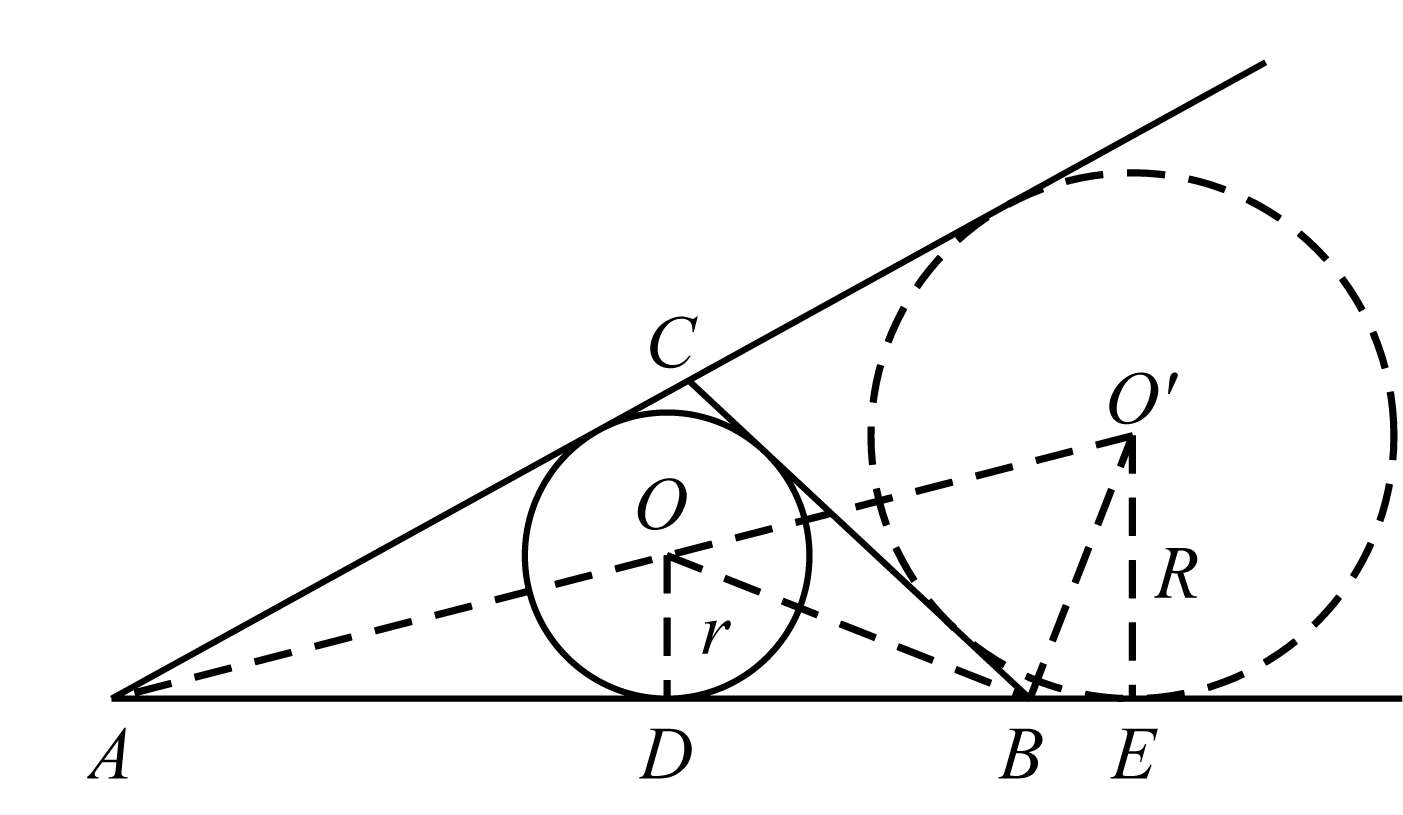
图6-2
所以 Rt △ BOD ∽ Rt △ O′BE ,
所以
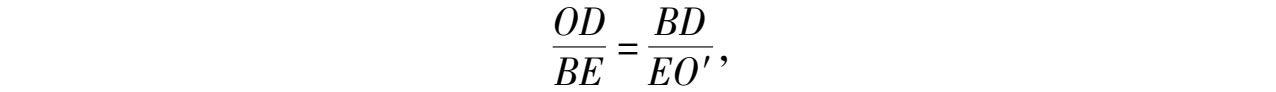
即
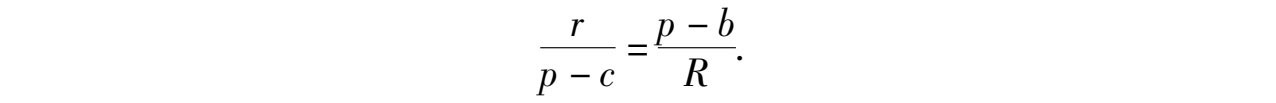
得
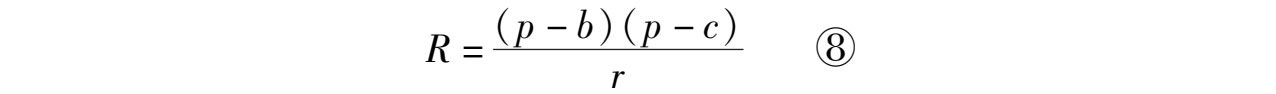
又△ AOD ∽△ AO′E ,
因为
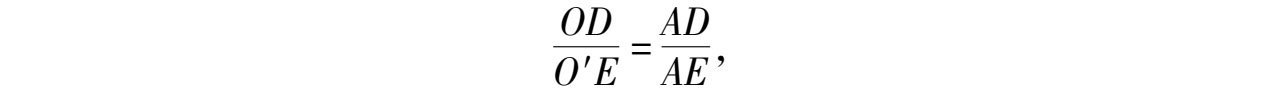
即

由⑧、⑨可得
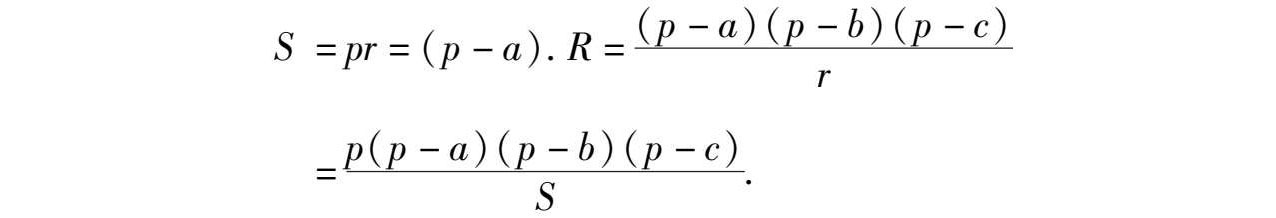
所以
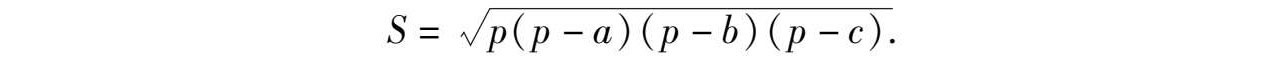
证法5 如图6-3所设,☉ O 为△ ABC 的内切圆,则
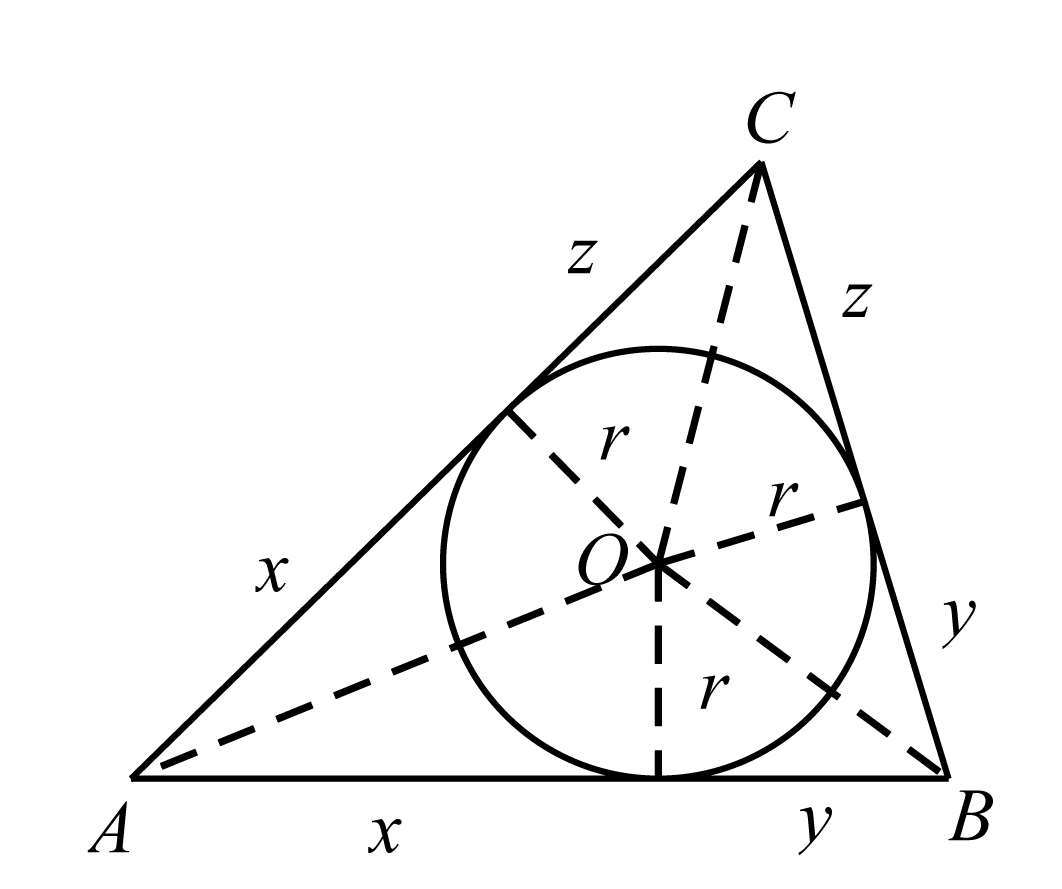
图6-3
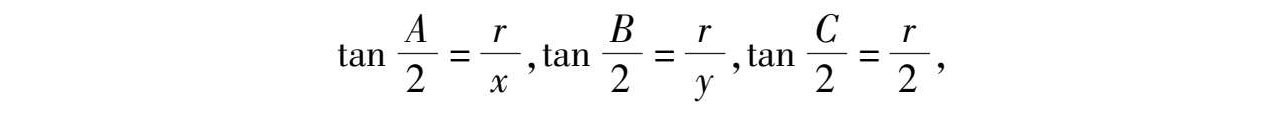
因为
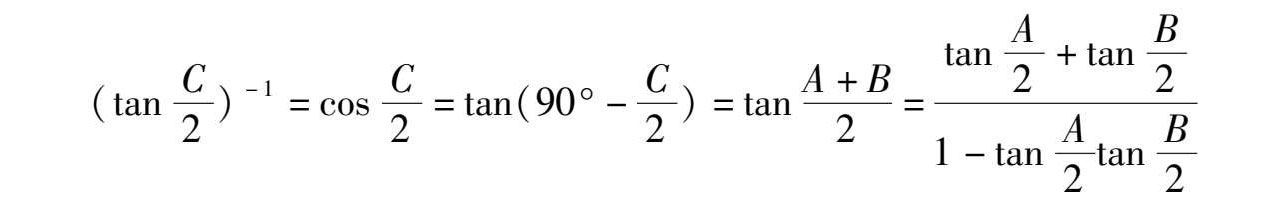
所以
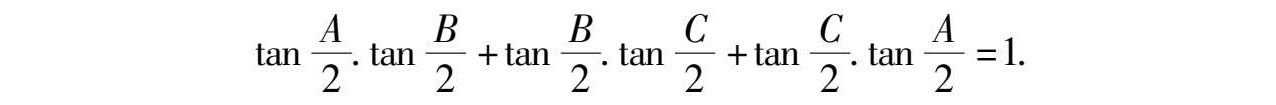
即有
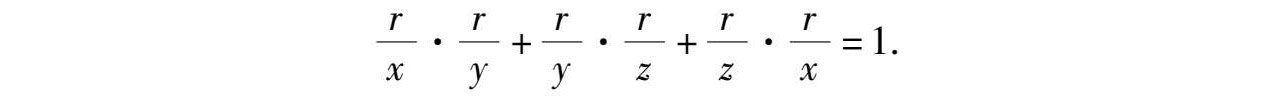
所以
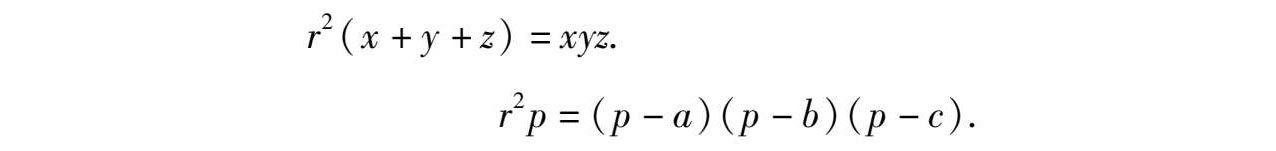
所以
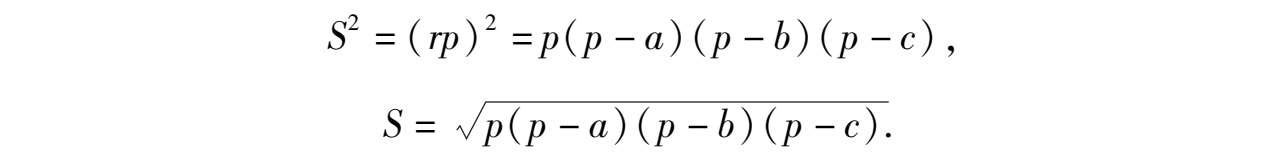
证法6 如图6-3,
因为
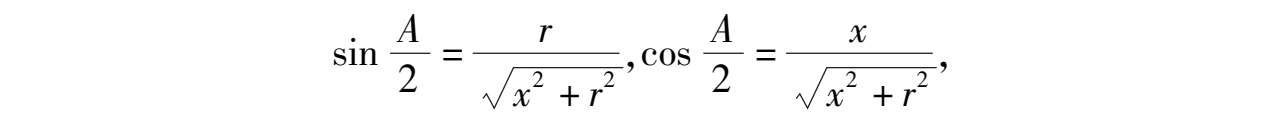
所以
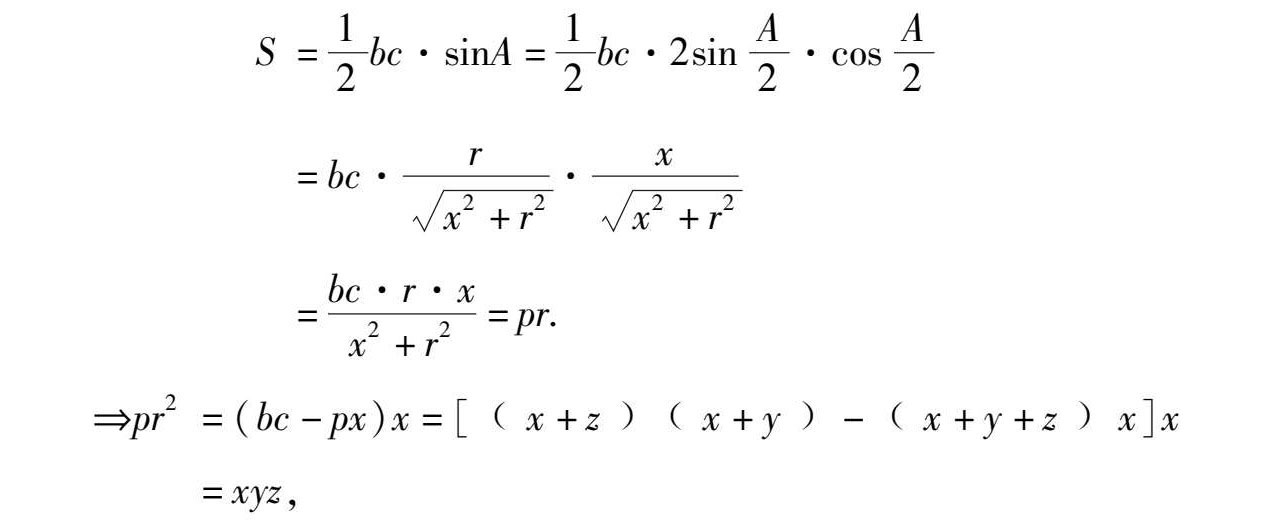
所以
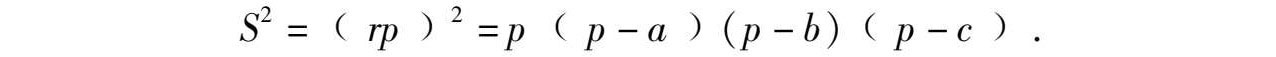
所以
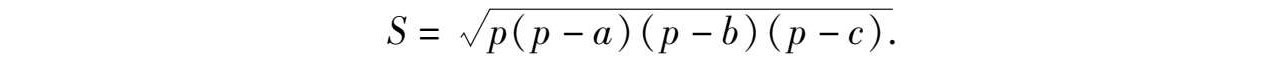
当然,本公式还有行列式证法、复数证法等其他方法.