




用塞瓦定理证三线共点问题有特殊效应.
例5.1 证明三角形的三条高交于一点.
证明 如图5-4,因为 α 1 = γ 2 , β 1 = α 2 , γ 1 = β 2 ,所以有
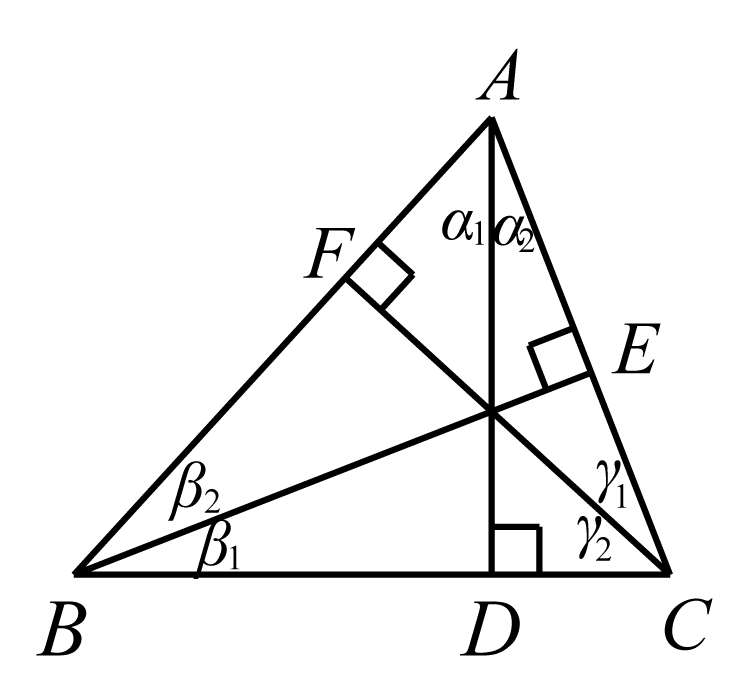
图5-4
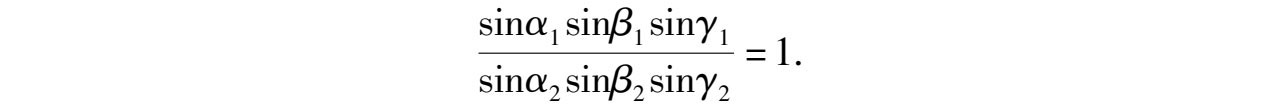
又 AC 、 BC 相交,故其垂线 AD 、 BE 不平行,由定理5.2,有 AD 、 BE 、 CF 共点.
例5.2 证明三角形三内角平分线交于一点.
证明 如图5-5,因 α 1 = α 2 、 β 1 = β 2 、 γ 1 = γ 2 ,所以
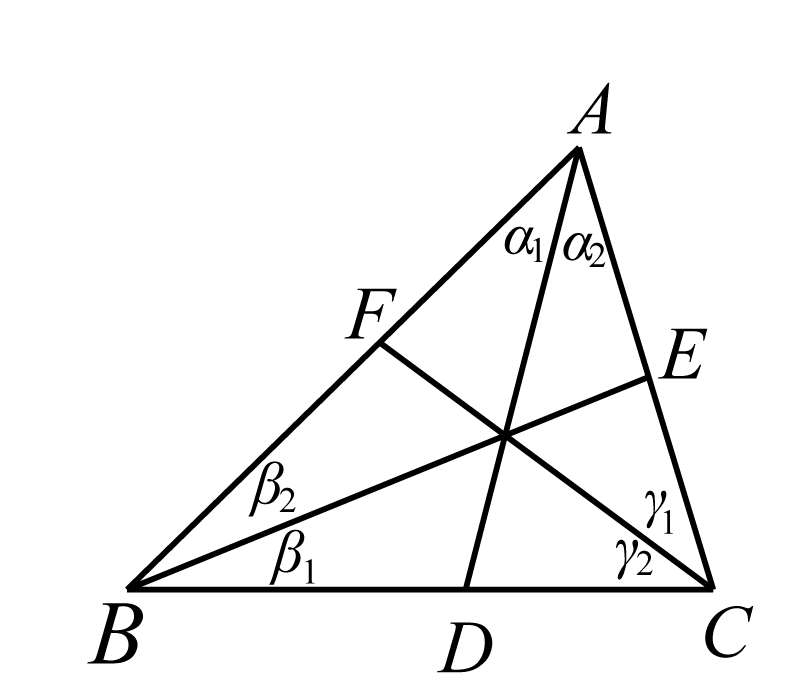
图5-5
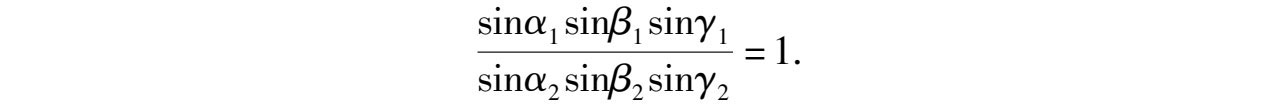
故三角平分线 AD 、 BE 、 CF 交于一点.
例5.3 设点 D 、 E 、 F 是△ ABC 的内切圆或旁切圆在边 BC 、 CA 、 AB 或延长线上的切点,则 AD 、 BE 、 CF 共点.
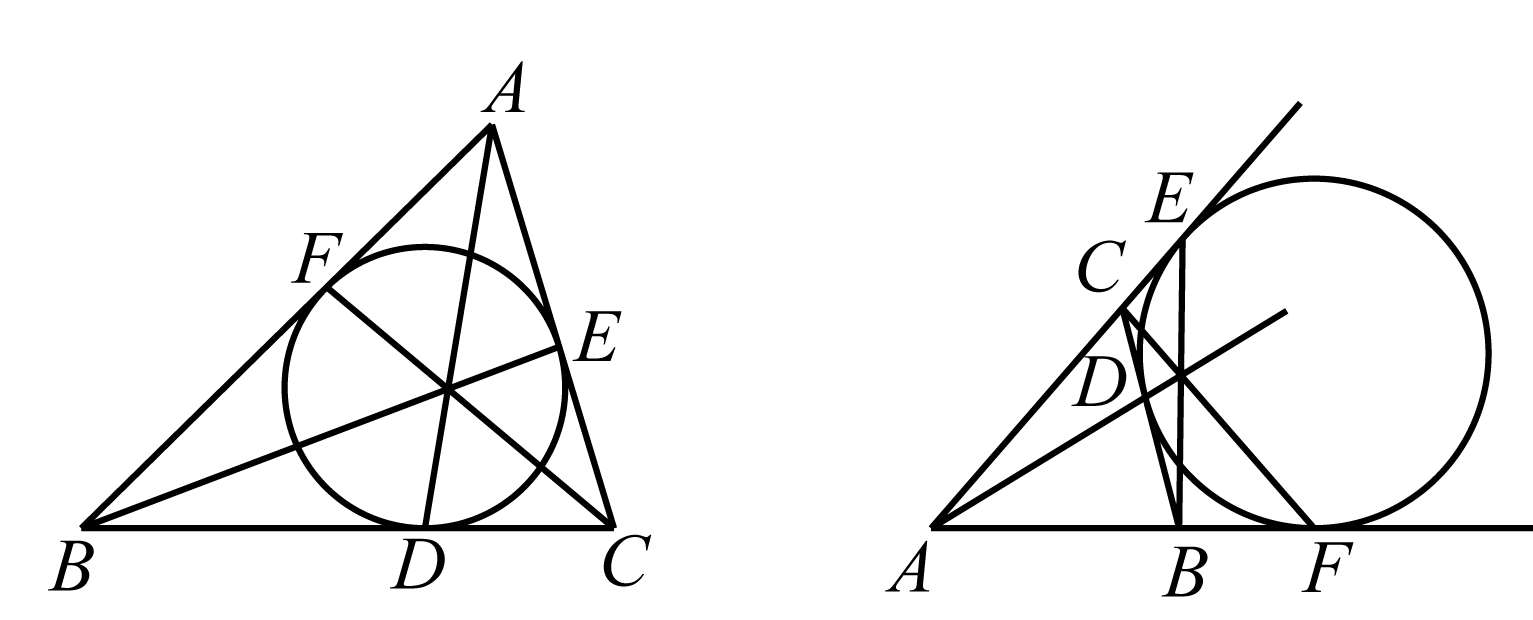
图5-6
证明 如图5-6,据切线长定理,有 EA = AF 、 FB = BD 、 DC = CE ,所以
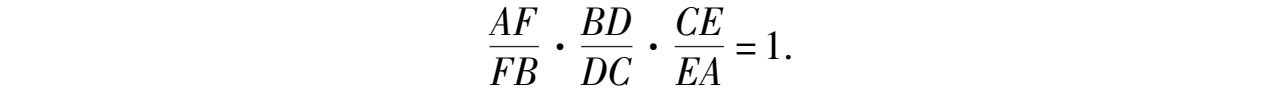
故 AD 、 BE 、 CF 共点.
例5.4 △ ABC 的三个旁切圆分别与边 BC 、 CA 、 AB 相切于点 D 、 E 、 F ,则 AD 、 BE 、 CF 共点(图5-7).
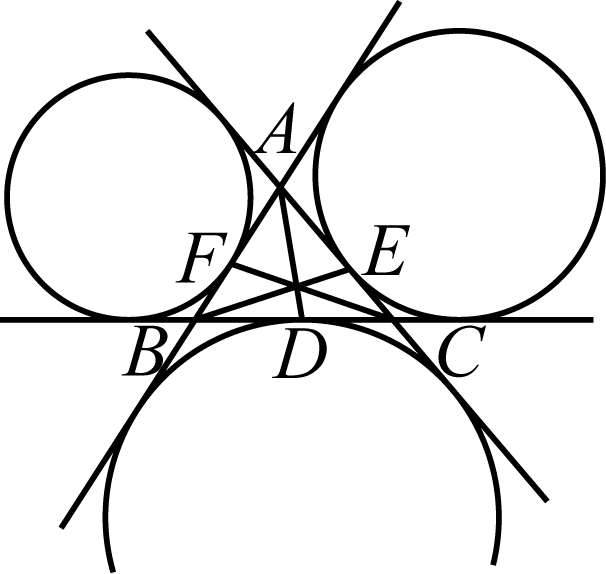
图5-7
证明
设△
ABC
三边为
a
、
b
、
c
,
p
=
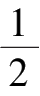 (
a
+
b
+
c
).
(
a
+
b
+
c
).
因为
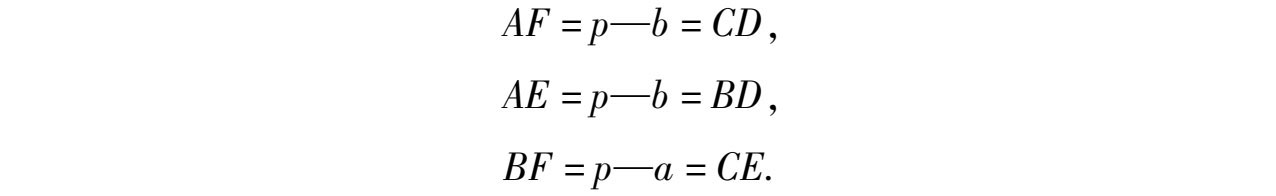
有
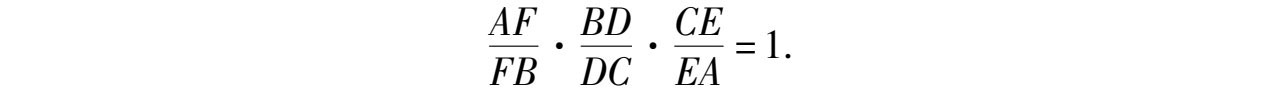
所以 AD 、 BE 、 CF 共点.
例5.5 通过三角形顶点并分(内分)对边成为与邻边平方成比例的两部分的直线交于一点.
证明 (如图5-8)设三边为 a 、 b 、 c .
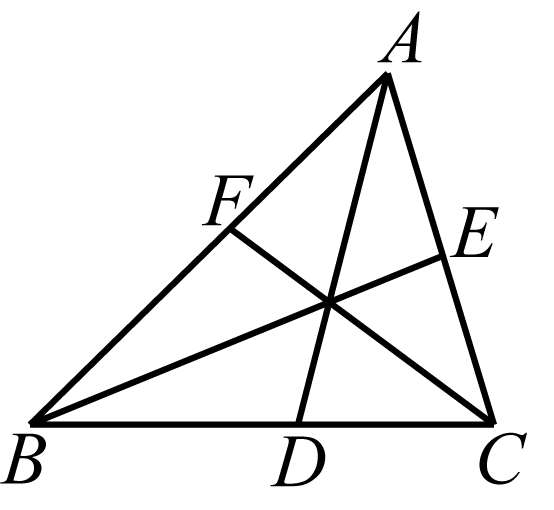
图5-8
因为
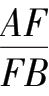 ·
·
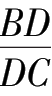 ·
·
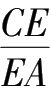 =
=
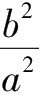 ·
·
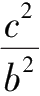 ·
·
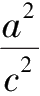 =1.
=1.
所以 AD 、 BE 、 CF 共点.
1.求证三角形三条中线交于一点.
2.平行于△ ABC 的边 BC 的直线交 AB 、 AC 于 D 、 E , BE 、 CD 交于 S .则 AS 的延长线必过 BC 边的中点 F .
3. S 为△ ABC 的中线 AF 上的任意一点, BS 交 AC 于 E , CS 交 AB 于 D ,求证 DE ∥ BC .
4.已知
D
、
E
、
F
分别为△
ABC
的
BC
、
CA
、
AB
边上的点,且
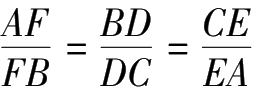 =2.
AD
与
BE
、
CF
交于
P
、
Q
,
BE
交
CF
于
R
,问△
ABC
的面积是△
PQR
面积的几倍?
=2.
AD
与
BE
、
CF
交于
P
、
Q
,
BE
交
CF
于
R
,问△
ABC
的面积是△
PQR
面积的几倍?