




下面我们解决几个与黄金分割有关的作图问题,其证明留给读者.
例3.1 求作边长为 a 的正五边形.
作法 (如图3-15)
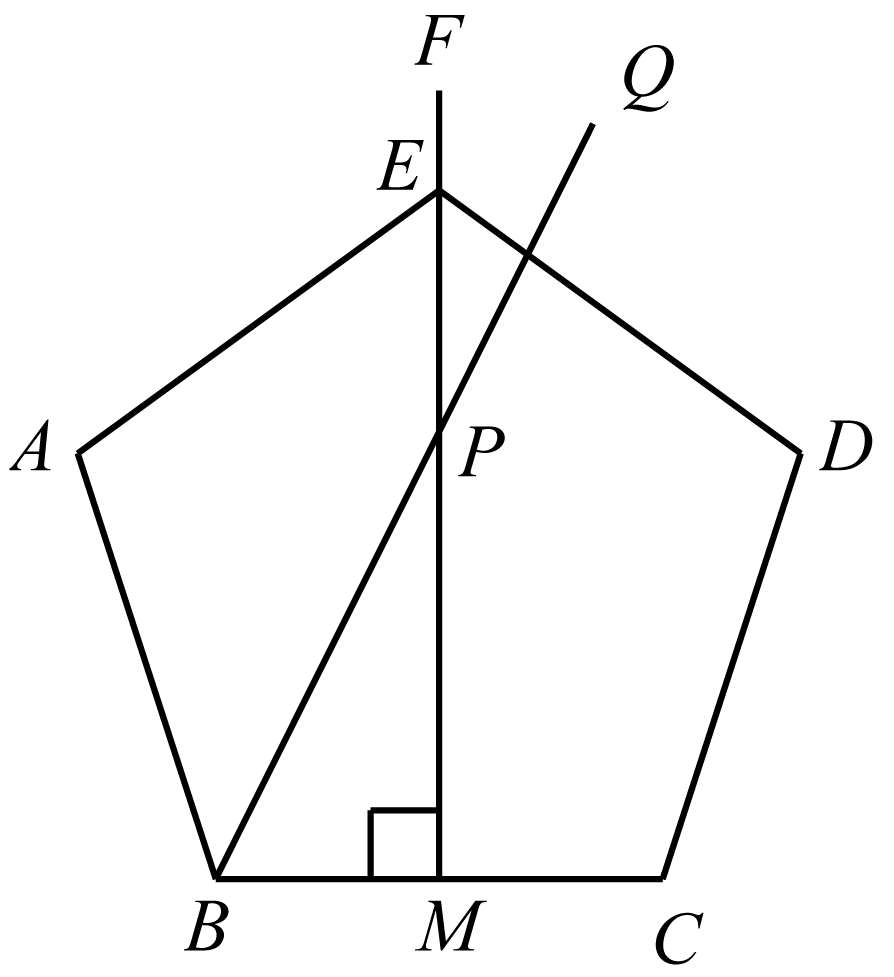
图3-15
(1)作线段 BC = a ,取其中点 M ;
(2)作 FM ⊥ BC ,且在 FM 上取点 P ,使 MP = BC = a ;
(3)联结
BP
延长至
Q
,使
PQ
=
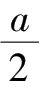 ,则
BQ
即为正五边形对角线的长;
,则
BQ
即为正五边形对角线的长;
(4)以 B 为圆心, BQ 为半径画弧交 MF 于 E ,则 E 为正五边形顶点之一;
(5)分别以 B 、 C 、 E 为圆心, a 为半径画弧得交点 A 、 D ,联结 AB 、 CD 、 DE 、 EA 即得所求正五边形.
例3.2 将半径为 R 的一己知圆十等分.
作法 (如图3-16)
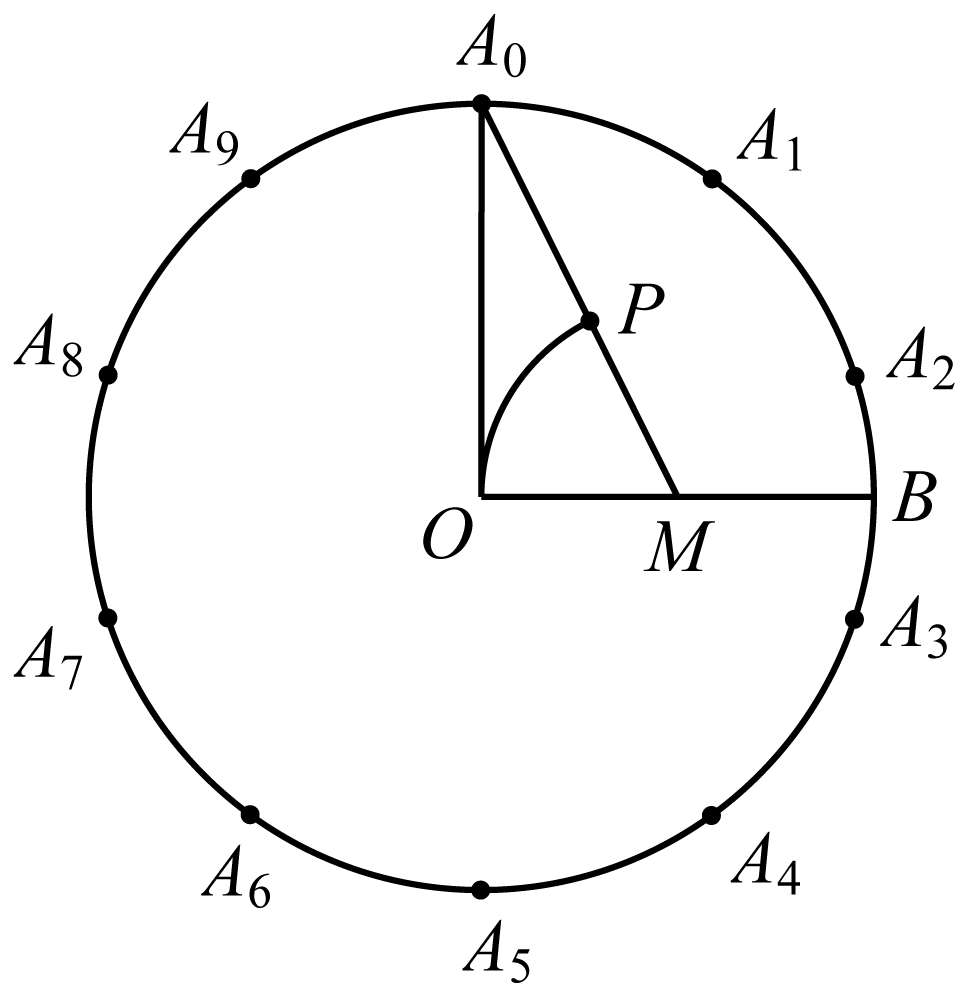
图3-16
(1)在☉ O 内取两条垂直的半径 OA 0 、 OB ;
(2)取 OB 中点 M ,连 A 0 M ;
(3)在线段
A
0
M
上取
MP
=
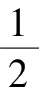 R
;
R
;
(4)从 A 0 起,以 A 0 P 为半径,在☉ O 上逐次截取可得 A 1 、 A 2 、 A 3 、…、 A 9 ,则 A 0 、 A 1 、 A 2 、…、 A 9 将☉ O 十等分.
例3.3 作已知圆的内接正五边形.
在例3.2中,隔点联结有关分点,则可得圆内接正五边形,但下面我们给出它的另一种作法,如图3-17.
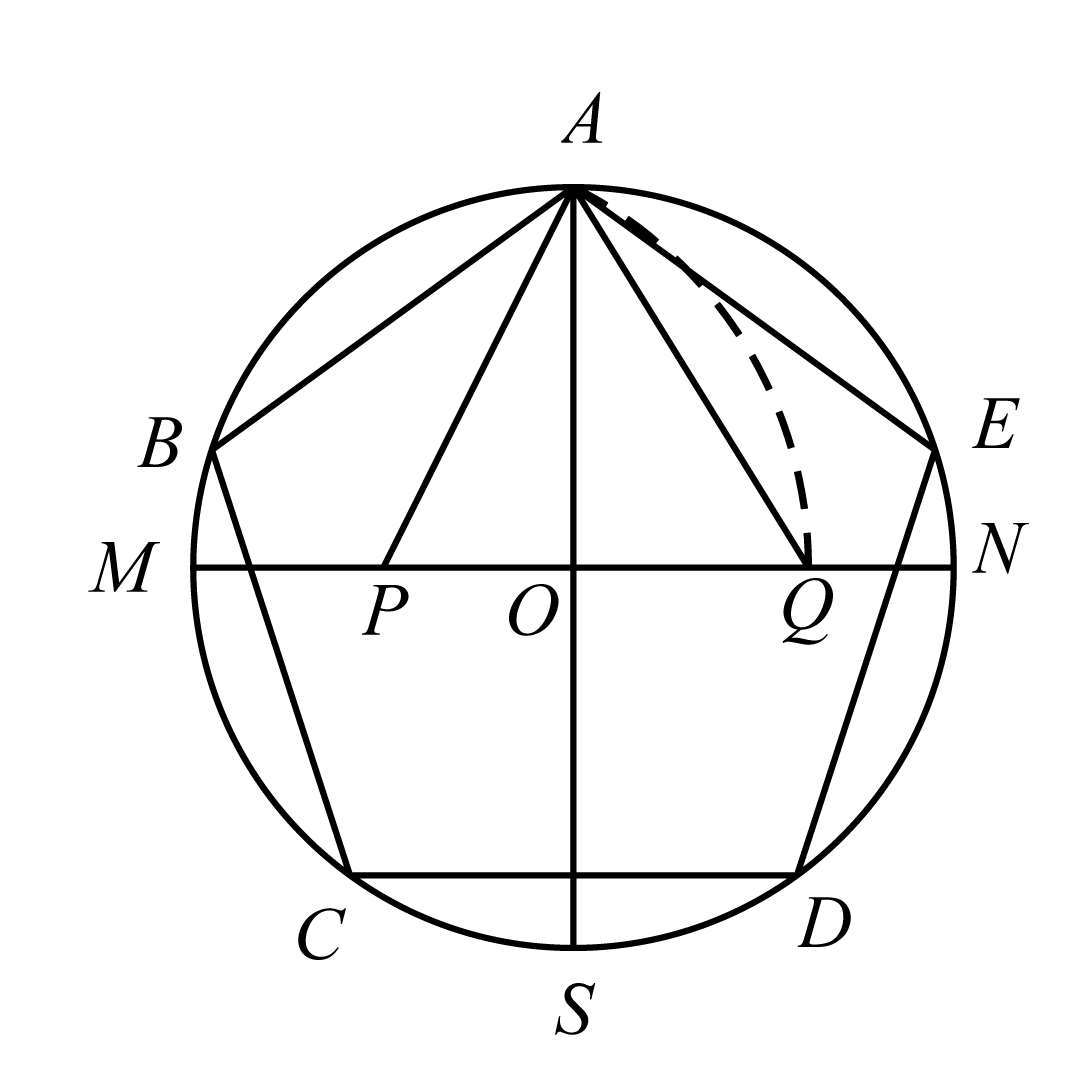
图3-17
(1)在半径为 R 的圆 O 内作互相垂直的两直径 AS 、 MN ;
(2)取 OM 中点 P ,联结 AP ;
(3)在线段 PN 上截取 PQ = AP ;
(4)以 AQ 之长在圆周上依次截取可得分点 A 、 B 、 C 、 D 、 E ;
(5)依次联结 AB 、 BC 、 CD 、 DE 、 EA 即得圆内接正五边形.
1.证明在图3-7中 M 、 N 分别为 BE 、 BM 的黄金分割点.
第2题图
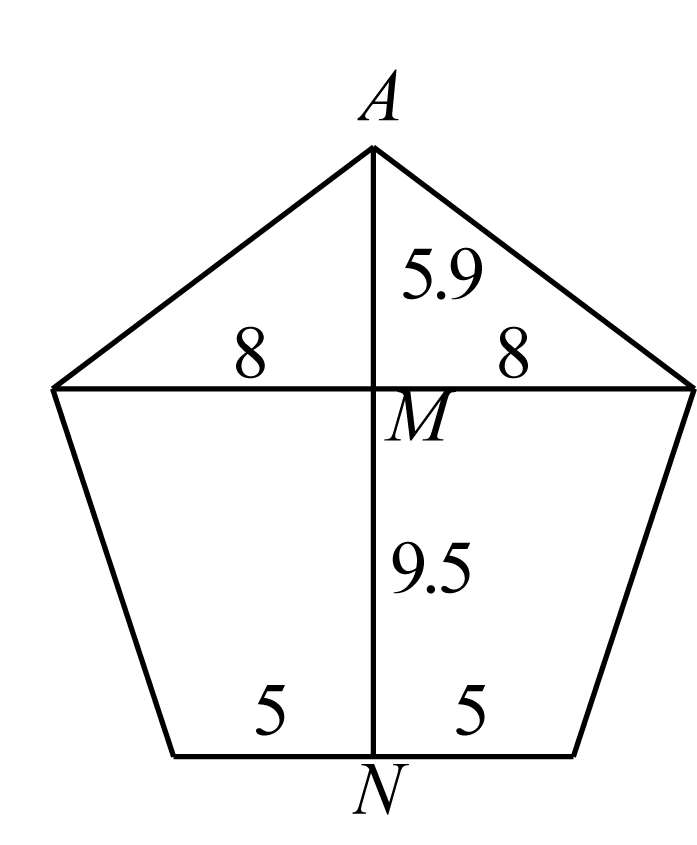
2.我国很早以前民间就流传一种正五边形的近似作法:“九五顶五九,八五两边分(如图).”这种作法的精确度是很高的.
(1)验证 M 点极接近 AN 的黄金分割点;
(2)试用这种方法作一边长为50毫米的正五边形.
3.验证黄金长方体的表面积与其外接球表面积的比为 ω ∶ π .