




下面我们给出黄金三角形、黄金矩形、黄金椭圆以及黄金长方体的概念,及其一些有趣的性质,但为节省篇幅,证明均略去.
前面我们已经提到,顶角为36 ° 的等腰三角形其底与腰之比等于 ω ,这样的三角形叫黄金三角形,黄金三角形还有下列性质.
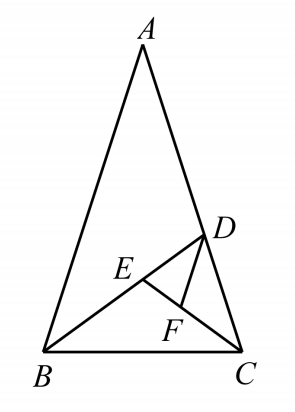
图3-11
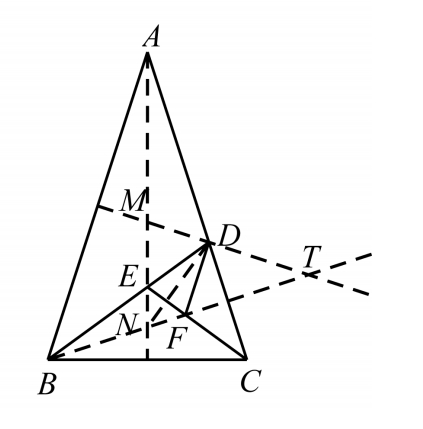
图3-12
(1)如图3-11, BD 为黄金三角形△ ABC 底角 B 的平分线,则△ BCD 也是黄金三角形;
(2)仿上作∠ C 的平分线交 BD 于 E ,则△ CDE 也是黄金三角形;如此下去可得一黄金三角形串:△ 1 ,△ 2 ,△ 3 ,…,△ n ,……,且所有的黄金三角形相似,其相邻的两黄金三角形的相似比为 ω ;
(3)在上述的黄金三角形串△ 1 ,△ 2 ,△ 3 ,…,△ n ,…中,△ n +3 的右腰与△ n 的左腰平行(如图3-11中,△ DEF 的右腰 DF 与△ ABC 的左腰 AB 平行);
(4)三角形串中△ n 、△ n +1 、△ n +3 的底边上的三条高共点(如图3-12,△ ABC 、△ BCD 、△ DEF 底边上的高 MN 、 NT 、 DN 共点);
与黄金三角形串{△ n }相邻的均是些底角为36 ° 的等腰三角形,他们也构成一三角形串,在这个三角形串中,相邻三个三角形底边上的高也构成黄金三角形(如图3-12,这个三角形串中的△ DAB 、△ EBC 、△ FCD 的高构成黄金三角形 TMN );这些黄金三角形也有一些有趣性质,这里就不一一列举了.
长宽之比为 ω 的矩形叫黄金矩形.
如图3-13, ABCD 为黄金矩形, AD =1, CD = ω ,则
(1) CD 是 AD 和 AD - CD 的比例中项;
(2)作正方形 ABFE ,则矩形 EFCD 仍为黄金矩形;再作正方形 EDHG ,则矩形 FCHG 也为黄金矩形,如此下去,可得一串正方形与一串黄金矩形(这反映了它的再生性);
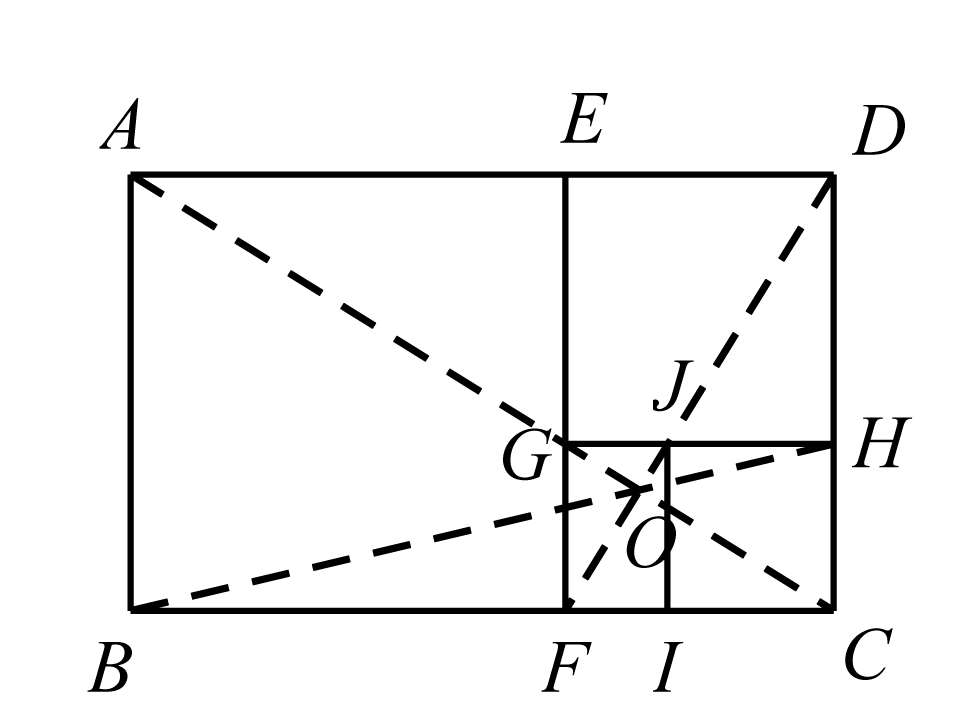
图3-13
(3)上面的正方形 ABFE 、 EDHG 、 CHJI 、…,构成一正方形漩涡,其边长组成等比数列: ω , ω 2 , ω 3 ,…,其面积和为矩形面积 ω (这给级数和 ω 2 + ω 4 + ω 6 +…﹦ ω 以几何解释);
(4)在上面的一串黄金矩形中,他们都相似,且相邻两矩形相似比为 ω ;
这串黄金矩形中还有如下性质:
(5) A 、 G 、 C 三点共线; D 、 J 、 F 共线;
(6) AC 、 DF 、 BH 共点,设为 O ;
(7) O 为所有黄金矩形的相似中心;
(8) AC ⊥ DF ;
(9)
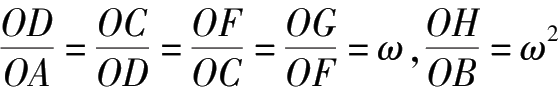 ;
;
(10)点
O
到
BC
的距离为
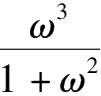 ,到
DC
的距离为
,到
DC
的距离为
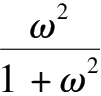 ;
;
(11)点 A 、 D 、 C 、 F 、 G 、 J 、…在同一对数螺线上.
若椭圆
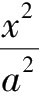 +
+
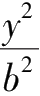 =1的短轴与长轴之比
=1的短轴与长轴之比
 =
ω
,则称此椭圆为黄金椭圆.以椭圆中心为圆心,
c
=
=
ω
,则称此椭圆为黄金椭圆.以椭圆中心为圆心,
c
=
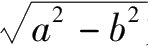 为半径的圆称为焦点圆.则
为半径的圆称为焦点圆.则
(1)黄金椭圆与焦点圆面积相等;
(2)椭圆与焦点圆在第一象限的交点为:
Q
(
b
,
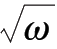 b
)(如图3-14);
b
)(如图3-14);
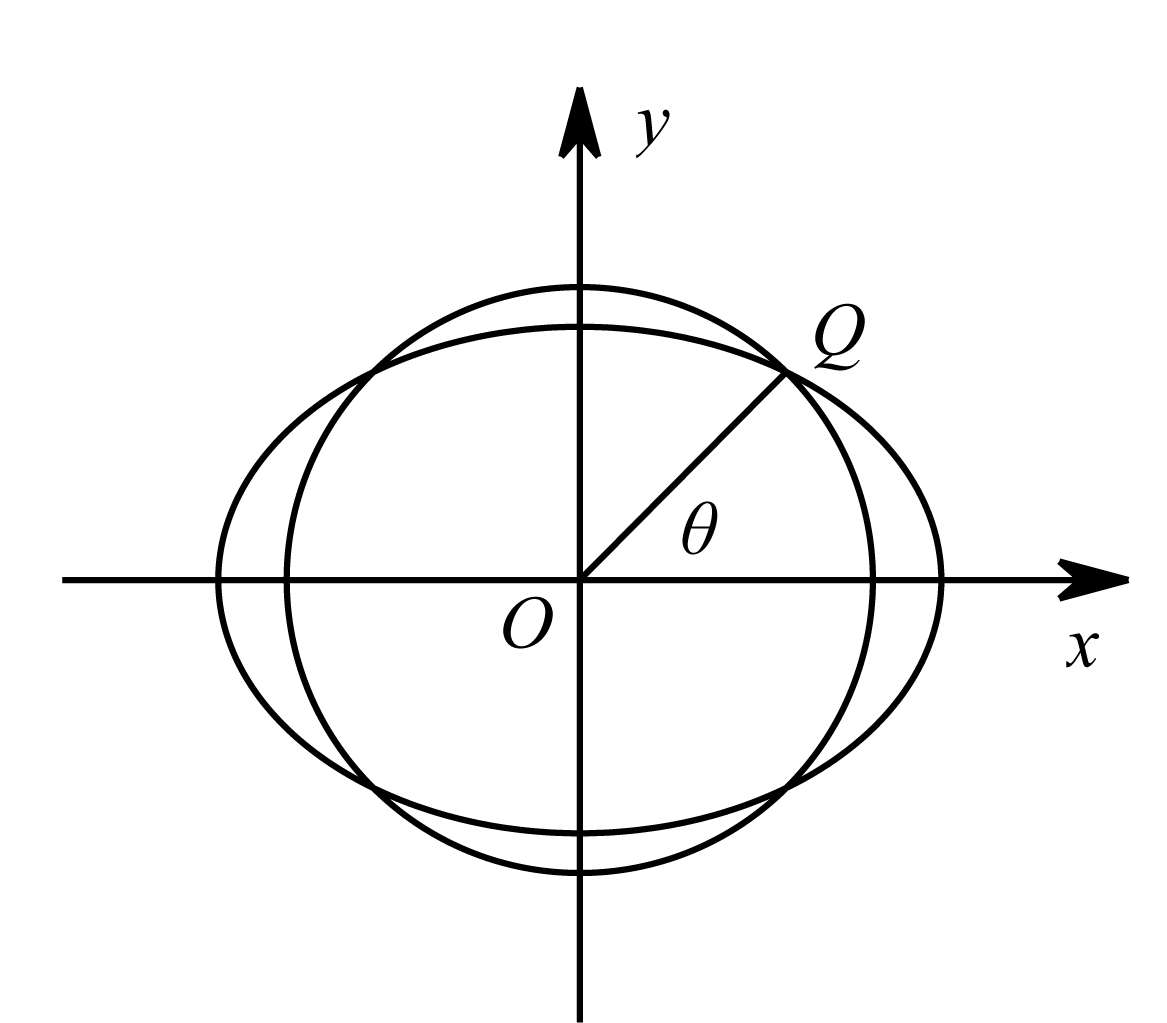
图3-14
(3)设
OQ
与
x
轴正向夹角为
θ
,则tan
θ
=cos
θ
=
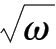 ,sin
θ
=
ω
;
,sin
θ
=
ω
;
(4)黄金椭圆的离心率
e
=
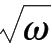 .
.
我们知道,二次曲线本是 π 的天下,岂知黄金数 ω 也在此有立足之地!
长,宽,高之比是
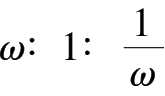 的长方体称为黄金长方体.黄金长方体的表面积与其外接球表面积之比是
ω
∶
π
.这里
ω
还与
π
建立起“亲缘”关系..
的长方体称为黄金长方体.黄金长方体的表面积与其外接球表面积之比是
ω
∶
π
.这里
ω
还与
π
建立起“亲缘”关系..