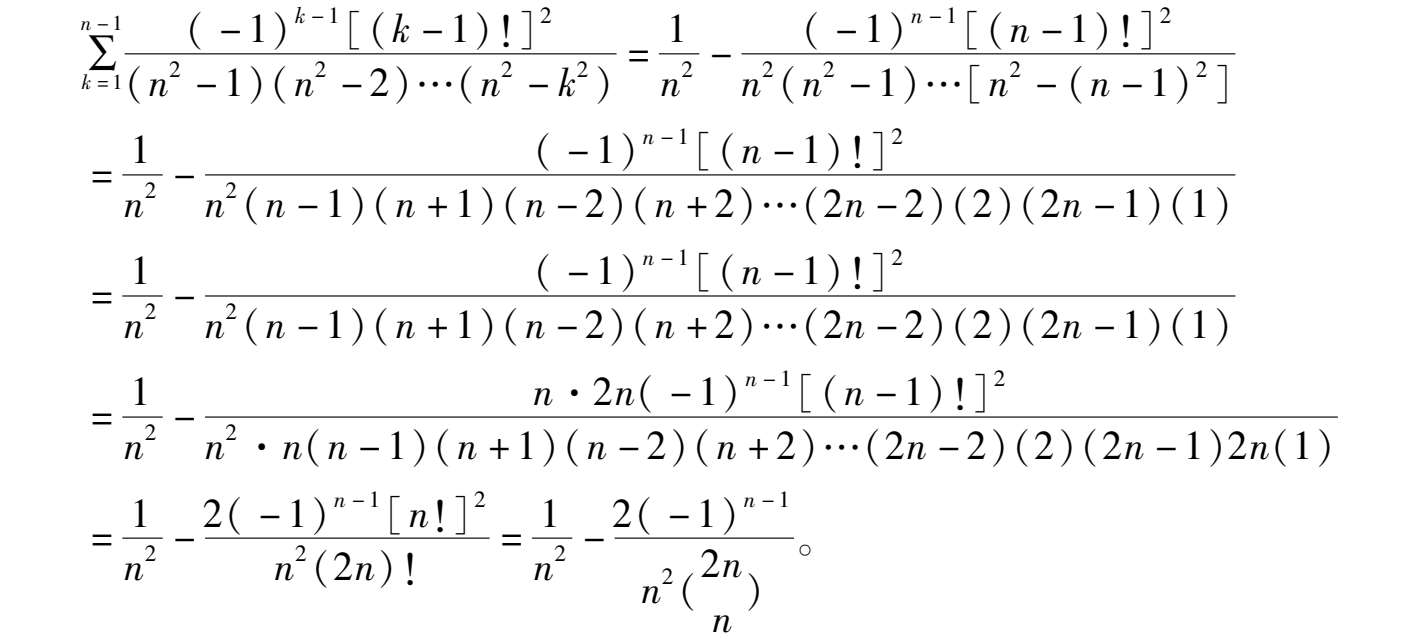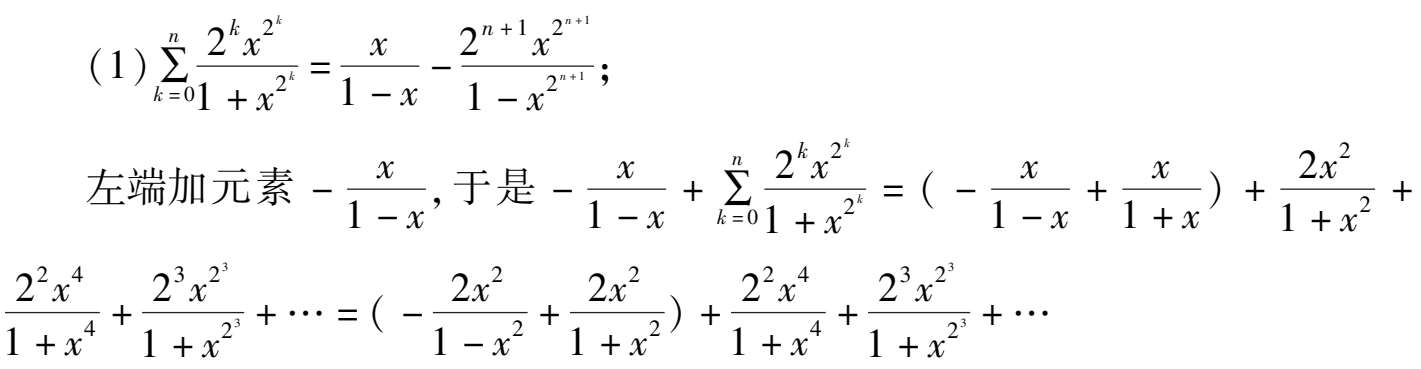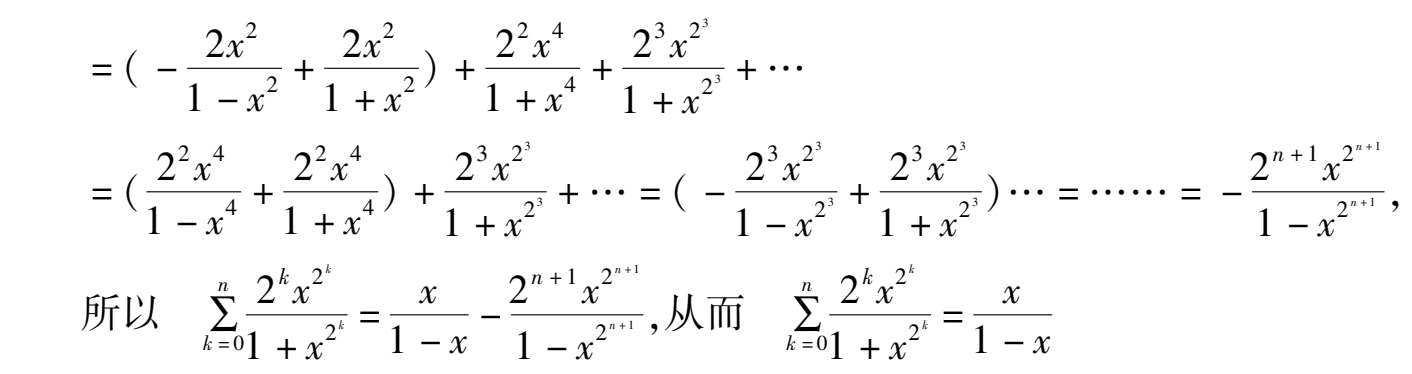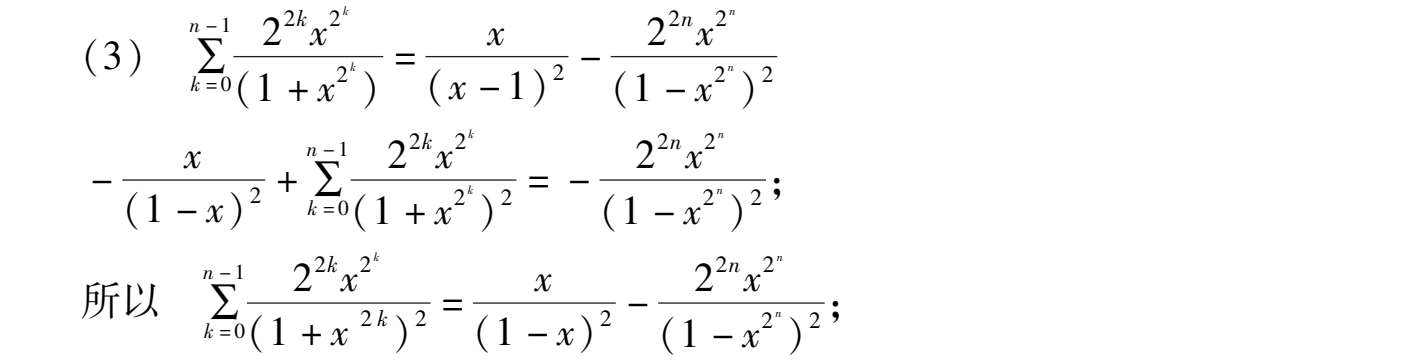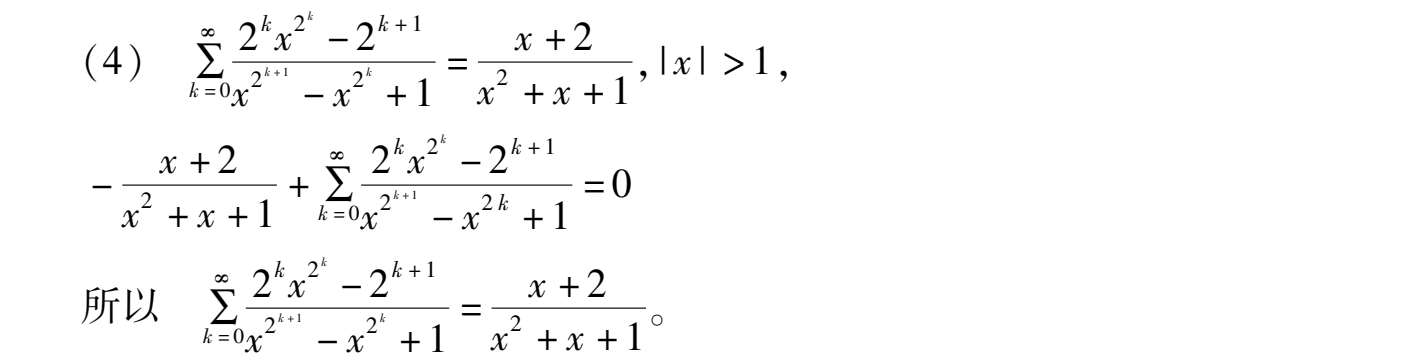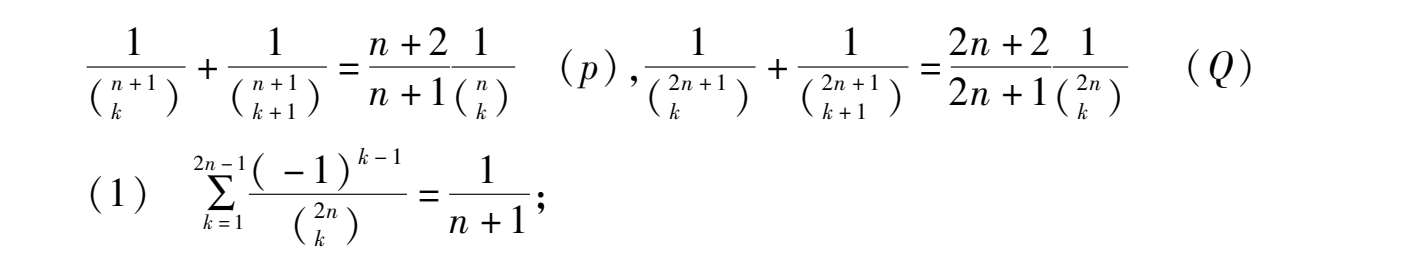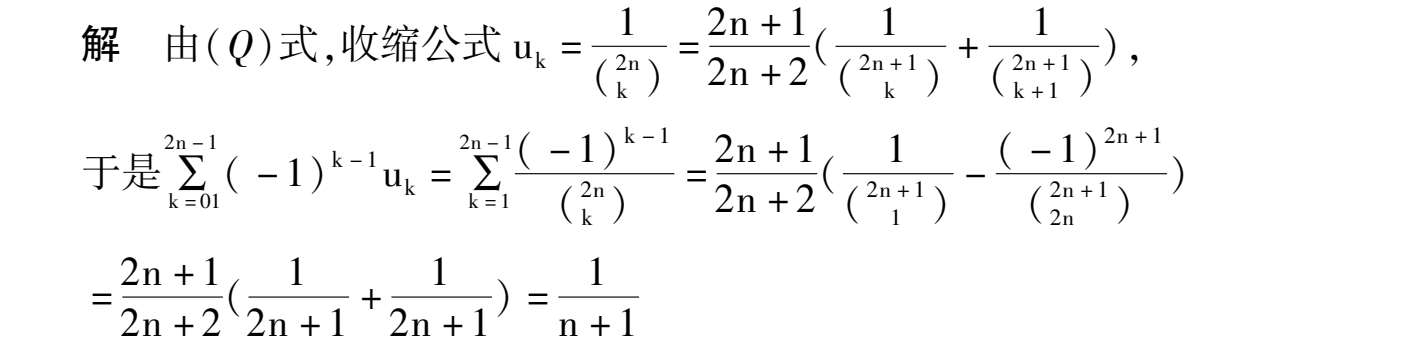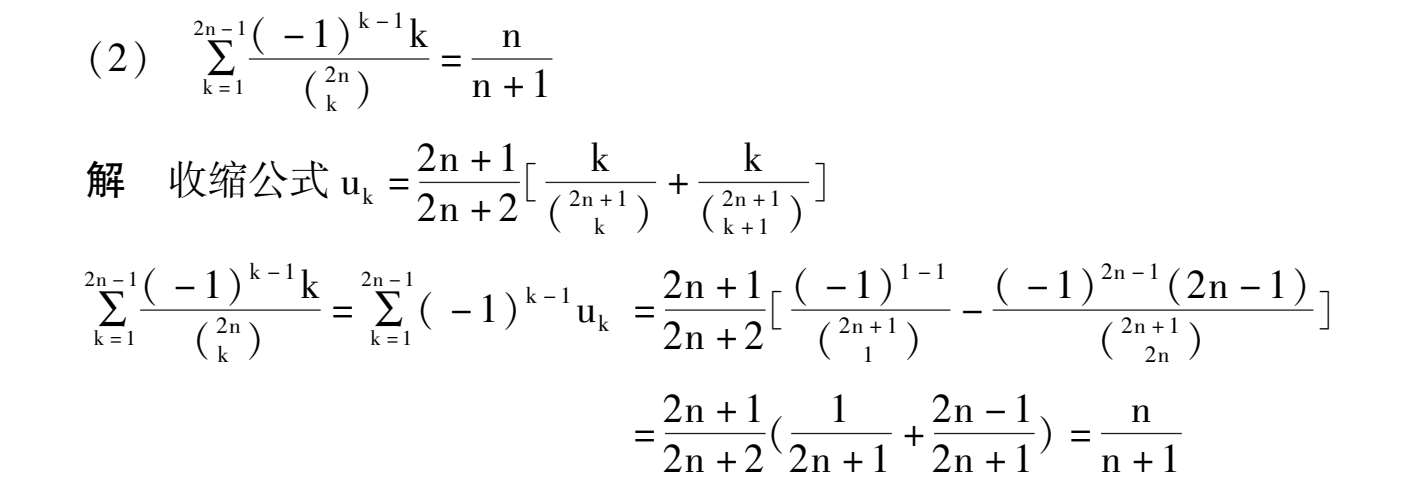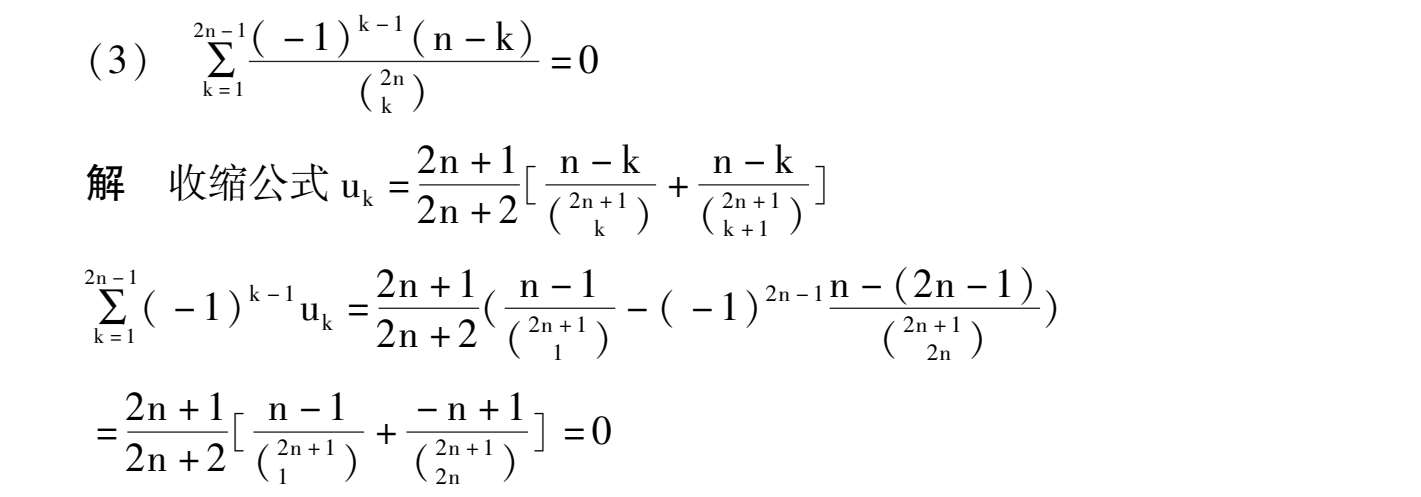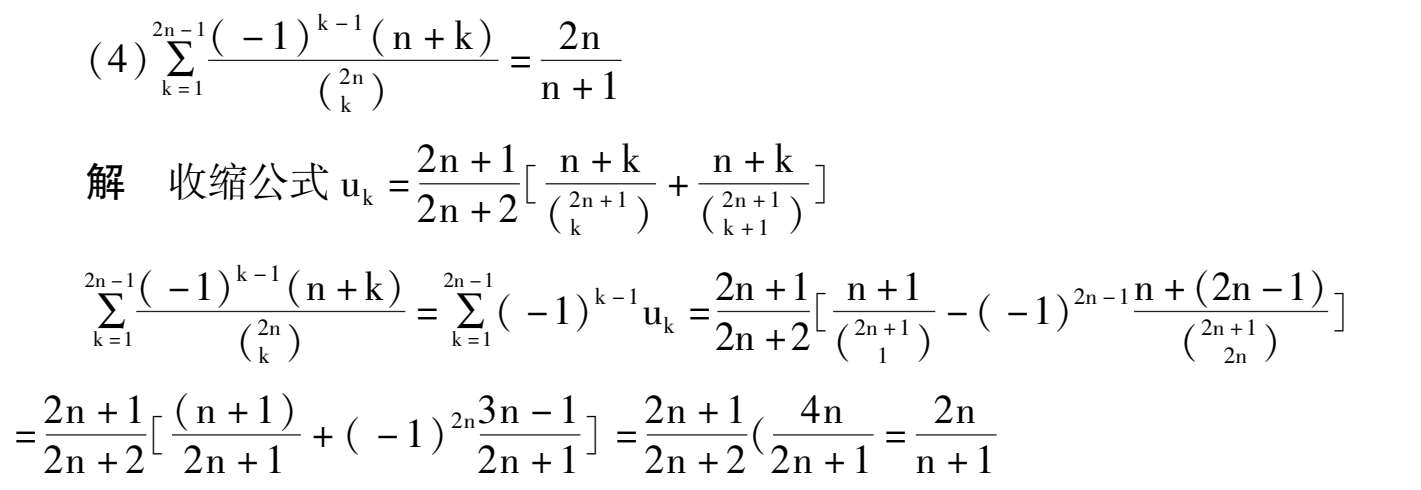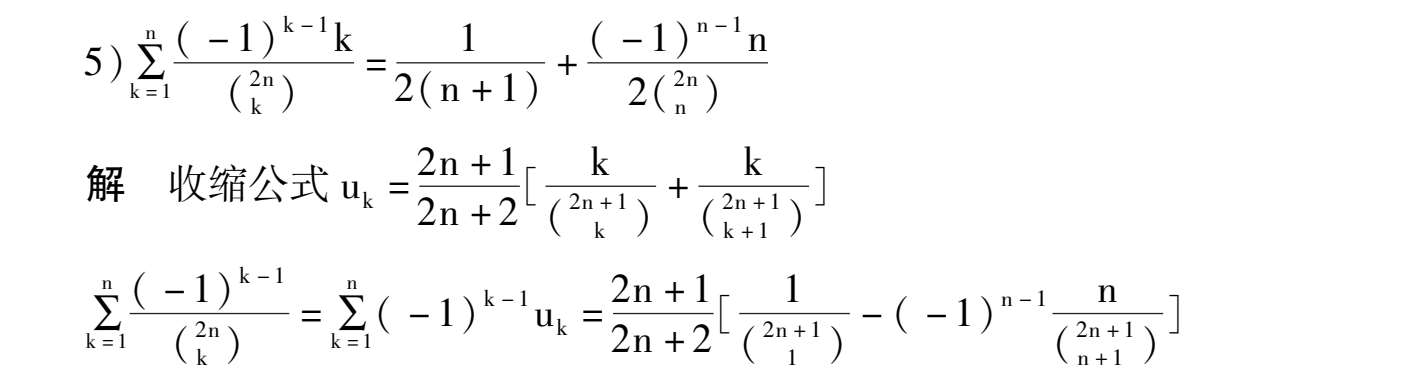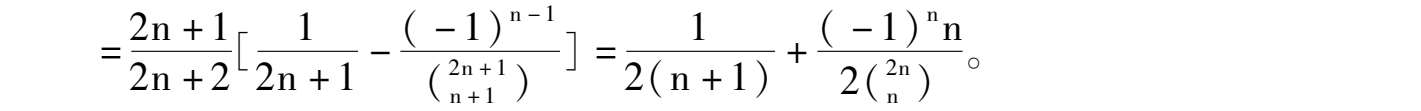如何将序列通项分拆成连续函数和或差,有如下收缩公式:
收缩公式1设
u
k
=
f
(
k
)-
f
(
k
+1),则
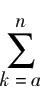 u
k
=
f
(
a
)-
f
(
n
+1),
n
⩾
a
;
u
k
=
f
(
a
)-
f
(
n
+1),
n
⩾
a
;
收缩公式2设 u k = f ( k )+ f ( k +1),
则
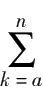 (-1)
k
u
k
=(-1)
a
f
(
a
)-(-1)
n
+1
f
(
n
+1),
n
⩾
a
;
(-1)
k
u
k
=(-1)
a
f
(
a
)-(-1)
n
+1
f
(
n
+1),
n
⩾
a
;
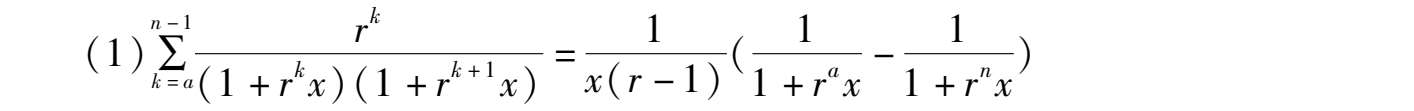
从通项表达式如何求得收缩公式 u k 是得到结果的关键。可用分式化成部分分式的方法。
设
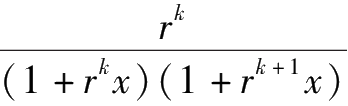 =
=
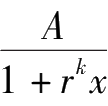 +
+
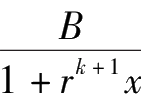 =
=
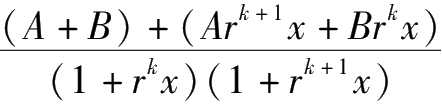 ,两端同次幂系数相等,
A
+
B
=0,(
Ar
+
B
)
xr
k
=
r
k
,
A
+
B
=0,(
Ar
+
B
)
x
=1;
A
=
,两端同次幂系数相等,
A
+
B
=0,(
Ar
+
B
)
xr
k
=
r
k
,
A
+
B
=0,(
Ar
+
B
)
x
=1;
A
=
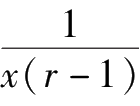 ,
B
=-
,
B
=-
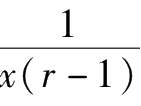 ;于是,得到
u
k
=
;于是,得到
u
k
=
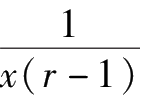 (
(
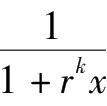 -
-
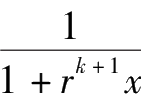 )。
)。
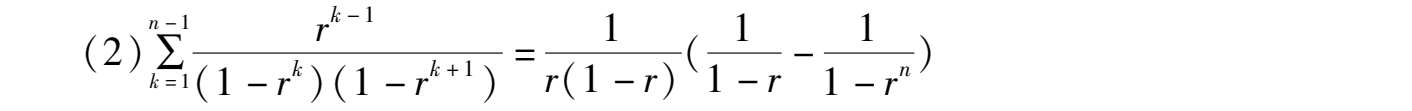
可得到收缩公式
u
k
=
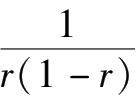 (
(
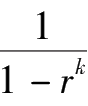 -
-
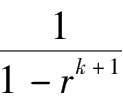 )。
)。
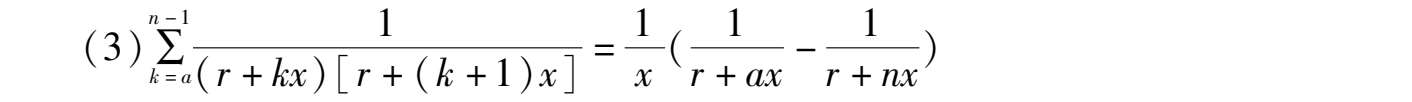
可得到收缩公式
u
k
=
 (
(
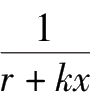 -
-
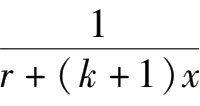 )。
)。
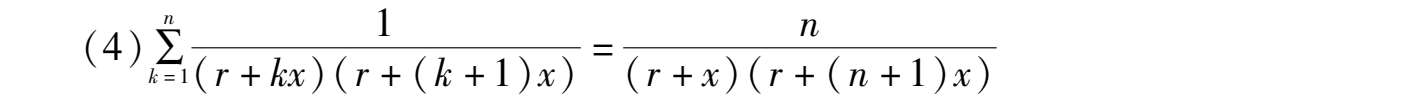
可得到收缩公式
u
k
=
 [
[
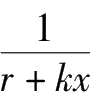 -
-
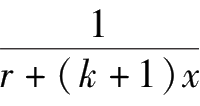 ]。
]。
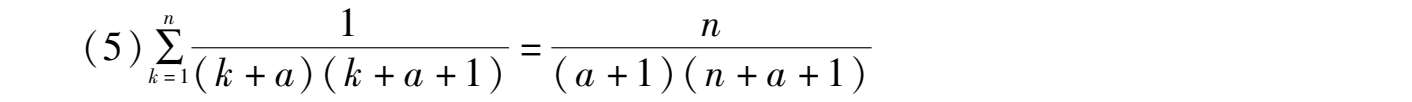
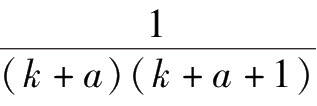 =
=
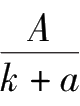 +
+
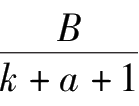 ,得到
A
=1,
B
=-1,从而
,得到
A
=1,
B
=-1,从而
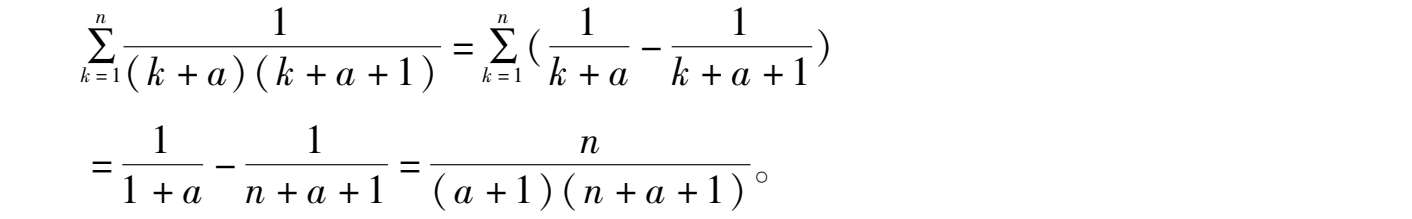
同法可得
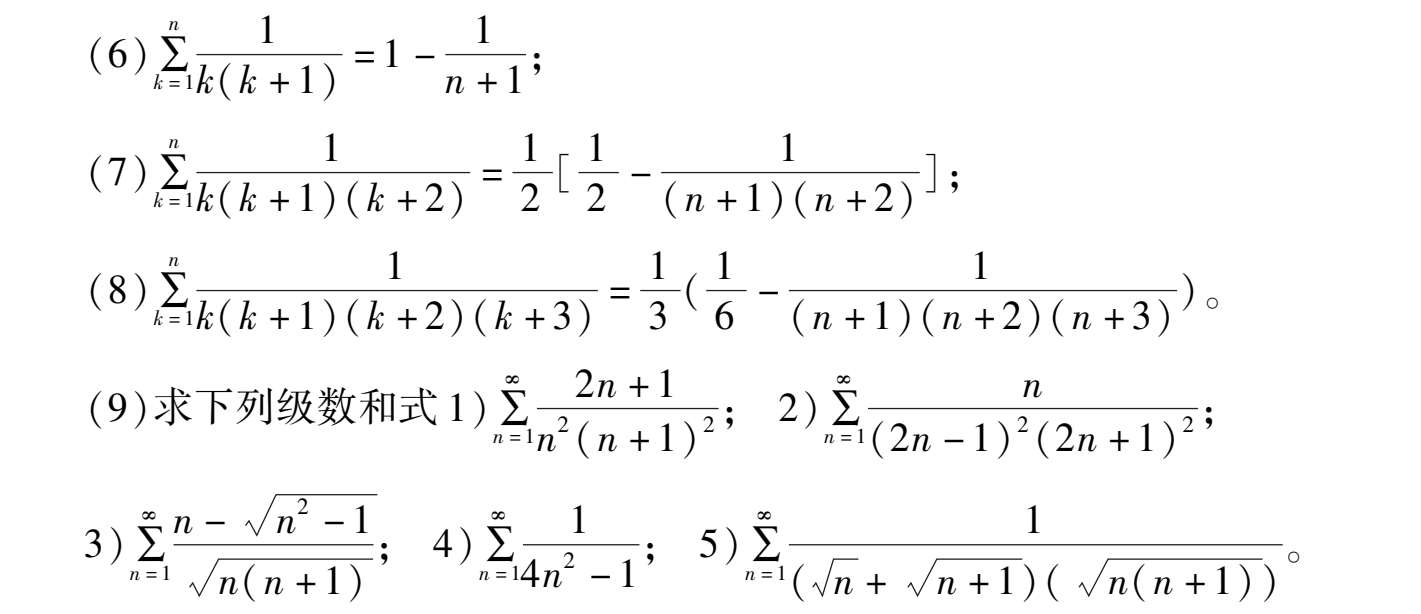
解 这类问题根据表达式特点,对通项进行裂项
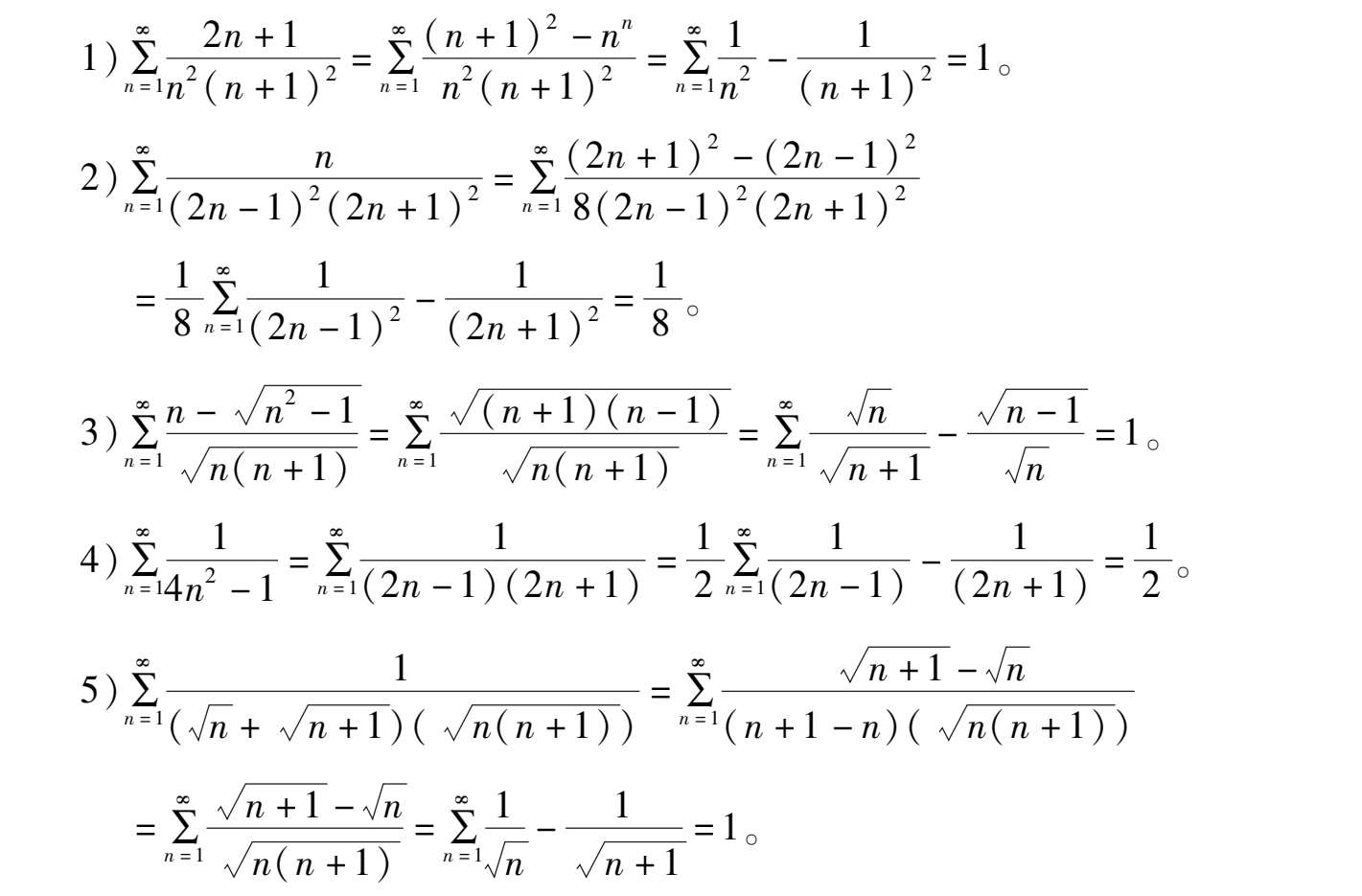

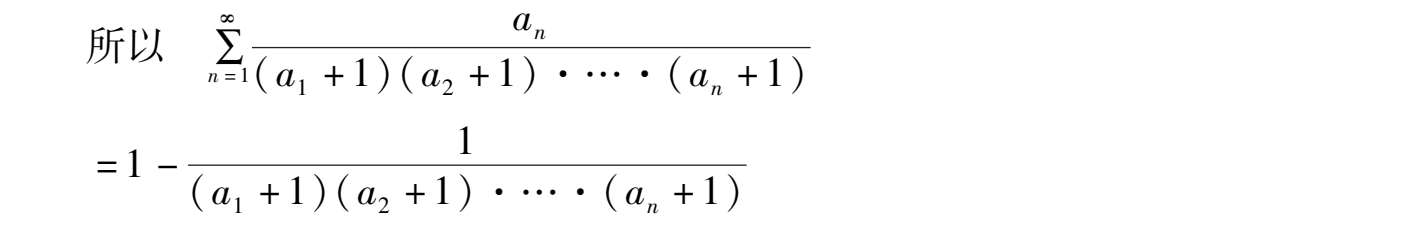
(11)证明
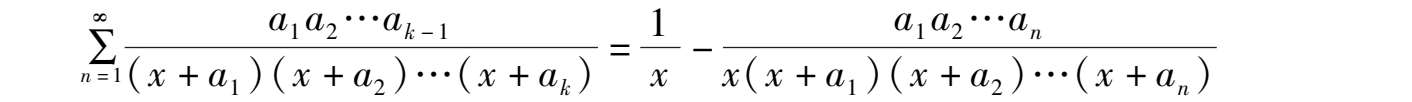
注意到右端为 A 0 - A n ,通项应为某两项之差即 A k -1 - A k ,
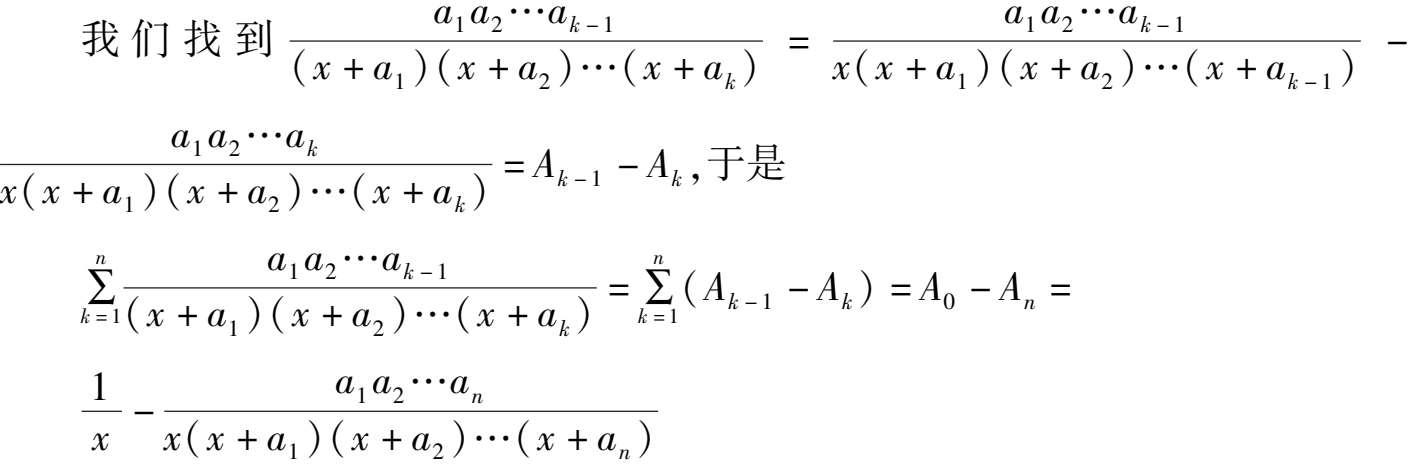
令 x = n 2 , a k =- k 2 ,