




题 1
写出一个二元一次方程组,使
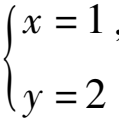 是它唯一的一组解.
是它唯一的一组解.
类型: 结论开放型
建议: 讲授方程组的定义的时候使用,要满足唯一的解,即方程组的系数不能成比例.
参考答案:
答案不唯一,例如
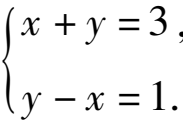
题 2
阅读材料:善于思考的小军在解方程组
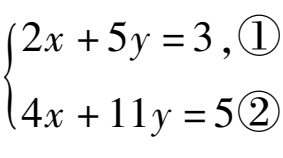 时,采用了一种“整体代换”的解法.
时,采用了一种“整体代换”的解法.
解:将方程②变形,得 4x + 10y + y = 5,
即 2(2x + 5y) + y = 5. ③
把方程①代入③,得 2 × 3 + y = 5,解得y = -1,
把y = -1 代入①,得 2x -5 = 3,解得x = 4,
∴原方程组的解为
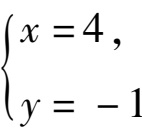 .
.
请你解决以下问题:
(1)模仿小军的“整体代换”的解法解方程组
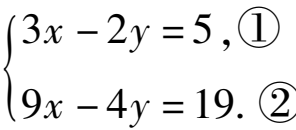
(2)已知x,y满足方程组
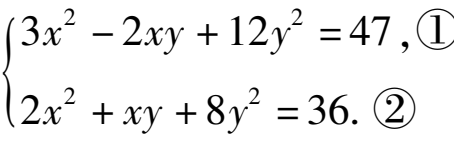 求x
2
+ 4y
2
的值.
求x
2
+ 4y
2
的值.
类型: 策略开放型
建议: 章节复习时使用.
参考答案:
解:(1)把方程②变形,得 3(3x -2y) + 2y = 19③,
把①代入③得 15 + 2y = 19,即y = 2,
把y = 2 代入①得x = 3,
则原方程组的解为
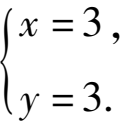
(2)由①得3(x
2
+ 4y
2
)= 47 + 2xy,即x
2
+ 4y
2
=
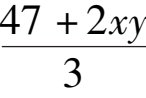 ③,
③,
把③代入②得:2 ×
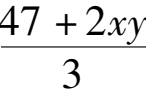 =36- xy,
=36- xy,
解得:xy = 2,
则x 2 + 4y 2 = 17.
题 3 仔细阅读下面解方程组的方法,然后解决有关问题:
解方程组
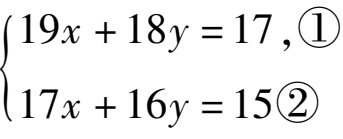 时,如果直接消元,那将是很烦琐的,若采用下面的解法,则会简单很多.
时,如果直接消元,那将是很烦琐的,若采用下面的解法,则会简单很多.
解:① -②得 2x + 2y = 2,即x + y = 1,③
③ × 16 得 16x + 16y = 16,④
② -④得x = -1,
把x = -1 代入③,得y = 2,
∴原方程组的解为
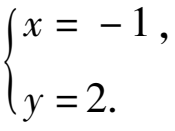
(1)请你采用上述方法解方程组
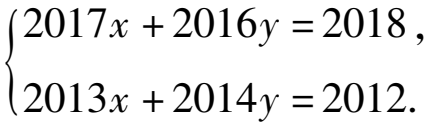
(2)观察以上方程组的特征,请你自己构造一个具有此特征的方程组,并用这个方法解方程组.
类型: 结论开放型
建议: 解二元一次方程组习题课使用,或留做课后阅读探究作业.
参考答案:
(1)
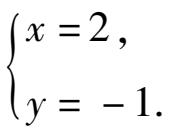
(2)答案不唯一.
题 4 商场打折前,买 30 件A商品和 40 件B商品用了 640 元,买 40 件A商品和 10 件B商品用了 680 元.打折后,买 500 件A商品和 500 件B商品用了 9600 元.请根据上述信息解决下列问题.
(1)打折前,A,B商品的单价分别是多少元?
(2)请在(1)的基础上提出一个能使用题目剩余条件解决的问题,并加以解决.
类型: 结论开放型
建议: 新授课使用.
参考答案: (1)A商品 16 元,B商品 4 元.
(2)答案不唯一,设问合理、解答正确即可.
例:打折后,购买 500 件A商品和 500 件B商品比打折前省了多少钱?
500 × 16 + 500 × 4 -9600 = 400(元).
题 4 如图 8 -1,长方形ABCD中放置 9 个形状、大小都相同的小长方形,求图中阴影部分的面积.
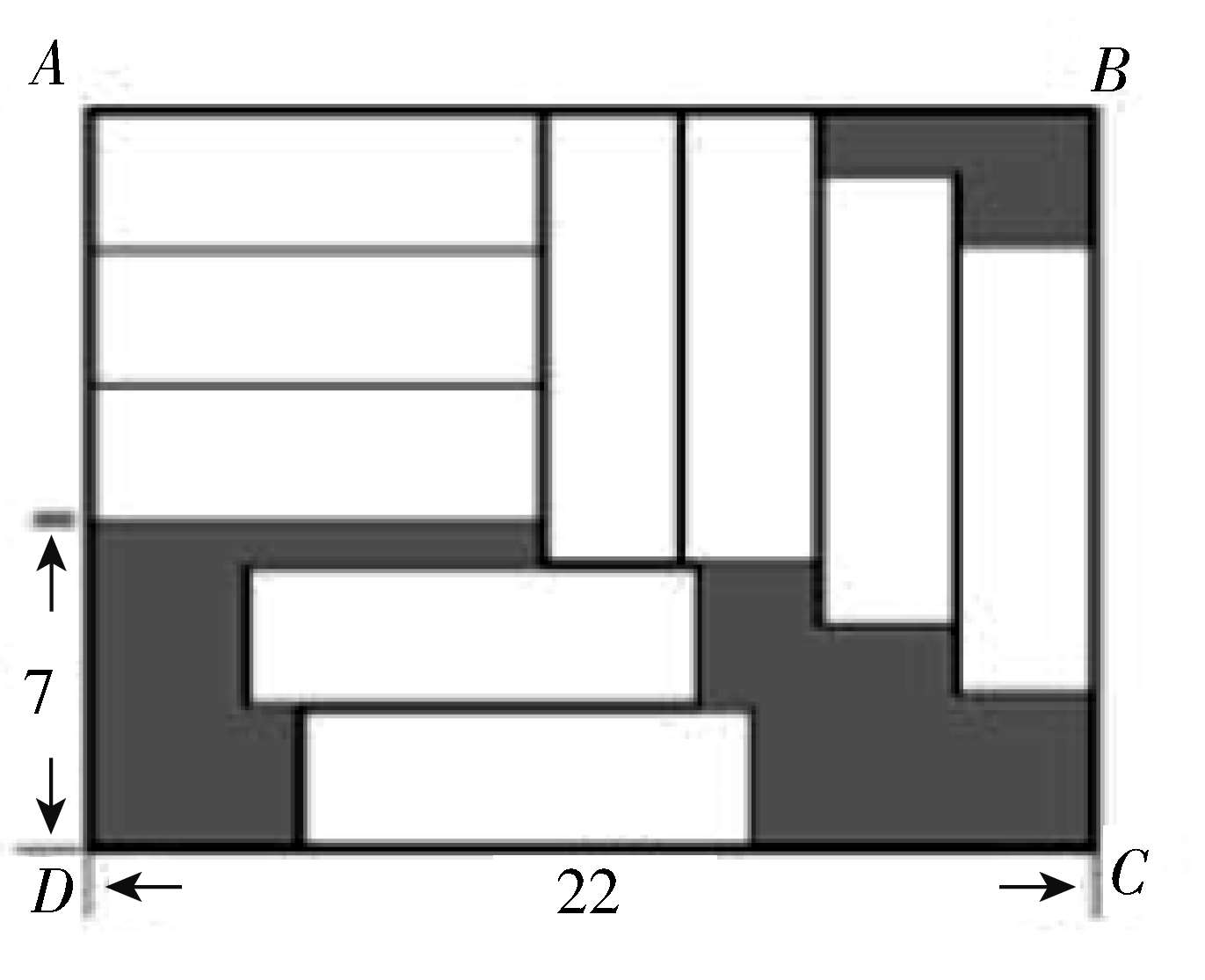
图 8 -1
类型: 过程开放型
建议: 新授课使用.
参考答案:
设小长方形的长为x,宽为y,则有x + 4y = 22,
即y = (22 - x) ÷ 4,①
又x + 2y = 7 + 3y②,将①代入②,得x + 2[(22 - x) ÷ 4]= 7 + 3[(22 -x) ÷ 4],解方程得x = 10,y = 3,大长方形的面积= 22 × (3 × 3 + 7)= 352,阴影部分的面积= 352 -9 × 3 × 10 = 352 -270 = 82.
题 5 (1)解下列方程组(直接写出方程组的解即可).
①
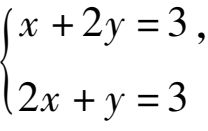 的解为______.
的解为______.
②
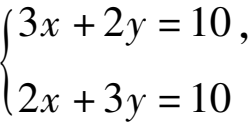 的解为______.
的解为______.
(2)以上每个方程组的解中,x值与y值的大小关系为_____.
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
类型: 结果开放型
建议: 复习课使用.
参考答案:
(1)①
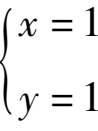
②
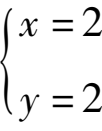
(2)以上每个方程组的解中,x值与y值的大小关系为x = y.
(3)答案不唯一,例如:
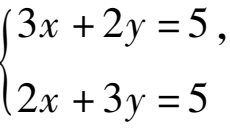 的解为
的解为
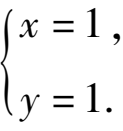
题 6 a、b取什么值时,方程(3x -2) a + (2x -3) b = 8x -7 有无数多个解?
类型: 策略开放型
建议: 1.该题的解决需要探索并发现一元一次方程有无穷解的条件,该题既可以作为一元一次方程起始课的拓展,也可以作为复习课使用.
2.该题目培养学生探索问题解决策略的能力,巩固一元一次方程和二元一次方程组的知识和技能.
参考答案:
先去括号,得:
3ax -2a + 2bx -3b = 8x -7,
移项,得 3ax + 2bx -8x = 2a + 3b -7,
合并同类项,得x(3a + 2b -8)= 2a + 3b -7.
要使方程有无穷多个解,必须满足:
(1)3a + 2b -8 = 0;
(2)2a + 3b -7 = 0.
解得a = 2,b = 1.