




Abstract :This paper presents a novel approach to non⁃optimum analysis based on experience recognition. Our goal is to provide support for optimization of uncertainty system. Our approach allows the practice courses and results of mankind are classified by their natures into two categories: optimum and non⁃optimum. It is considered that the non⁃optimum system does not exclude the targets and the results of optimum in practice. The formation of non⁃optimum system serves as the basis for existence of optimum system in uncertainty. Besides, the various characteristics and functions of the optimum system can be measured from the non⁃optimum system. At the same time, it also puts forward the non⁃optimum measurement of the system along with non⁃optimum tracing and self⁃learning of the experience systems.
Keywords : Non⁃optimum category, man’s recognition, new methodology, actual significances
The theory of the non⁃balanced self organized system has been put forward and is developing in the past more than ten years. This shows that any system is in the nonbalanced open system. Prigogine founded the Theory of Dissipation Structure, Harken formed the science of synergetics. They all succeeded in putting forward the theory of non⁃balanced self⁃organized system. The common special feature is the study of, in the non⁃balanced⁃open system, when the system and circumscribed circle have matter and energy to exchange, how the macro time, space or time⁃space ordered structure and functional⁃ordered further study of the laws of the evolution from order to confusion.So, the theory of non⁃balanced self⁃organized system, starting from the study of the balanced⁃open system which the objective world proper possesses, reflects truly the whole internal mechanism and the common principle of the ordered and functional ordered structure in various time⁃space. According to the self⁃organized system principle, an ordered system may go into confusion, and naturally, it is very important to study the reasons, ways and confusion is necessary for us, we have to control its speed, so that it may be fitter for our needs; if it is harmful for us, we have to take some measures to prevent it from going into confusion, and manage to make it more ordered. The higher degree of development is the systematic optimization.
That is the purpose of studying this system. So the lower degree is the nonoptimization. According to the theory of “dissipation structure”, as long as the system is open, the non⁃balanced state may become the source of ordered system. So the nonoptimum category, can it come into the stage, where we are to seek the optimization.The thinking of the optimum emerges and develops in the course of man’s knowing and reforming of objective world. Examining the process of optimum concept, we may find that at the beginning of its emergence and formation, people knew little about its connotation, and with the development of human society, the knowledge will get deeper.
The first concept of the optimization was only judged by comparison with one another; and now the concept of the objective function under a certain control. But actually, the optimization project or system which best represents the objective function bears only relative significance, that is, they are realized under a certain and strict condition. Because of the complication of mans, social practice (many undetermined and uncertain factors, alternation and the influence by his behaviors) and the feasibility of the pursued goal in present circumstances. This makes the optimum methods only be applied in limited scope.
That is to say, in a certain scope, it is easier to realize the optimum system. But for come more complicated systems, as for social economic system, not so easy.Because in these systems, there are often many contradictory aims and needs, together with many limiting factors which are hard to be determined. So you can by no means find the best plan suitable for all the aims and needs. And on the other hand, because of people’s subjective views and behaviors, systematic aims are influenced by both internal and external environment. Sometimes it is hard to achieve the quantitative optimization. So, in the recent years, some have posed the viewpoint of “satisfaction”.That is, we don’t have to pursue the optimum state. Only when the system is satisfactory, enough has been done. The satisfactory optimum method actually is a special phenomenon of non⁃optimum system.
We’ve had some tries in this way and come to conclusion: the theory of extended optimum systems and non⁃optimum system.
We have gone farther in the study of optimum system to make the theory of optimization more useful in practice.
Man’s knowledge of the objective world and of himself is always in the midst of ever deepening course. In human history, there has been many a social practice that was carried out partly or even wholly with blindness, thus making it impossible to avoid failures completely. Yet, each of the failures adds to the improvement of human understanding of the objective and subjective world. So those social efforts that have failed occupy important positions in the chronicle of human knowledge. The motto“failure is the mother of success” tells that human race learns from setbacks. But it fails in theorization and quantitative analysis. From the system science point of view,all systems exist in a risk state. In the past, people mainly studied how systems operate under the conditions of may accept and how they can become stable. Yet these stabilization is only relative and on many occasions the conditions for it is uncertain and unattainable. So the efforts of seeking this kind of stabilization are rather blindfolded,and facts have proved that merely controlling some of the conditions can not keep the system free of unstable factors, because some or even all of the variables to satisfy a stable system may become unstable, and on the other hand conditions made for the unstable systems may help to stabilize. For example, cutting cost and raising output value may make the firm more efficient, but they may make it unstable too ( funds turnover getting difficult and initiative lower, etc. ).
So if we on one hand try to control the system in a stable state, and watch for the unstable factors on the other, we may not only supplement and substitute the conditions for the stable system, but also help to build a new stable system, which are what systematology is all out for. In the past few decades, with the development and application of computers, the so⁃called optimizing technique has been widely used in technological fields with obvious results. However, those optimum models or systems that have achieved their target functions are optimum only under very specific and strict conditions. Although people have extended this method to many areas, the optimum results can only be temporary and even impossible sometimes, the main reason being illustrated in the stability analysis above. So the traditional optimum methods have their problems which must be analyzed and solved with all dimensions considered.
Our purpose is to develop a concept of relative optimum (RO) and threes optimum hold (OT), with the RO including the “non⁃optimum” (NO),“sub⁃optimum” (SO) and the “ optimum” ( O), following the theory of unity of the opposites. Thus the human practice processes and results are divided, according to their nature, into O, SO and NO sections. From these three directions we can best study the features and rules of system optimization.
3.1 Measurement method
There are two sides to everything, and the final direction of the system can be only achieved through practice and the transition of the two sides. The state of the system decides its goal by choosing between optimum and non⁃optimum. Hence the nonoptimum problem is illustrated through the following method:
Suppose So represents an optimal system, Sno a non⁃optimal system. No matter it is an optimal system or a non⁃optimal system, they are all composed of system objective O , system function G and system environment E . As to the optimal system, if the structure Л ( O , G , E ) of the sub⁃optimum ( cannot make sure of the condition of optimum and non⁃optimum) of the system S composed of objective O , function G and environment E meets the following conditions:
(1) The objective of the system can be attained;
(2) The function of the system can be achieved;
(3) The environment of the system can be controlled.
Then S is called an optimal system. The attainability of the objective of the system shows that the distance between the recognized goal of the system and the actual goal of the system is acceptable. The achievability of the function of the system refers that the actual functional resources is near to the objective⁃required resources.The controllability of the environment of the system refers to the self⁃organizing capacity, or the order parameters achieving the permitted value.
Suppose O r is recognition goal of the system, O s acts as the actual goal of system, α represents the difference of the value between O r and O s , which shows the degree of acceptance of the goal of the system. G s acts as the system’ s actual functional resources, G r acts as the resources demanded by the system’ s objective, and β expresses the functional measurement value between G r and G s ; The entropy of the actual system e≤ γ , and γ expresses the system’ s standard entropy. Thereby for the system’s sub⁃optimum structure Л ( O , G , E ), if there are ε , ζ , η ,(random minimal discrepancy can be accepted) causing | α - α 0 | ≦ ε ,| β - β 0 ︱≦ ζ ,| λ - λ 0 | ≦ η to hold at the same time, the system S is an optimal system. α 0 , β 0 , λ 0 is the border value of the system’s optimum and non⁃optimum, and thereby the gathered assemble Л ( α 0 β 0 λ 0 ) is the criteria of the system’s non⁃optimum analysis. In the actual system analysis, under certain selected standards ( ε , ζ , η is known), for α , β , λ , when man can’t obtain α 0 , β 0 , λ 0 , the system S is called non⁃optimum system.
The above is the overall description of the non⁃optimum problem of the system,which tells how to decide the overall frame⁃saw in the non⁃optimum system. However,different measurement and means have to be applied in different systems to solve actual problems. Proper quality and quantity determining methods are applied in the actual system analysis. Furthermore, artificial intelligence and expert system reasoning tools can play important roles in non⁃optimum system analysis.
One of the emphases on the non⁃optimum analysis theory is to describe the borders of the optimum and non⁃optimum category quantitatively. Because the borders change with objective conditions and subjective desire of mankind, and human being has different behavior parameters, they always appear as uncertain under dynamic.Meanwhile, because of the continuous progress of mankind’s practice and recognition,under cooperating of the widely exchanged scientific information, the borders might become certain and describable during the dynamic changes. As to the judgment of the reasonability and accountability of the described borders, it is no a theoretical problem,but a problem of selecting the methods and checking the practice. In addition, when analyzing the problems of the system through quantitative methods, a lot of relationship parameters need to be statistically analyzed and attributably appraised. In many aspects, the influences of the system’ s non⁃optimum are depended largely on the experience accumulated in the recognition of the system. That is to say, experiential analysis plays an important role in the non⁃optimum system analysis, which reflects the meaning and function of the combination of the nature and quantity evaluation.
3.2 Models analysis
In the references [1-6], we discussed the relationship between the system nooptimum and the optimum. However, since all systems are sub⁃optimum in their nature, our aim is set on the problem of system’ s optimization and non⁃optimum. As we have said, a system that is optimum in one time and space environment may be nonoptimum in another. The behavior of a system is almost circling around the cycle from the unbalanced state to the balanced, from the disordered to the ordered overcoming“ups and downs” and “ disruptions” to reach its “ destination point” or“ destination ring” in its reciprocal space. Soothe non⁃optimum (NO) types.
(1) Systems formed from the changed states of the systems’ old self in the process of system movement. The former constraint conditions are no longer in keeping with the operating conditions of the new systems, because the systems now operate in the NO.
(2) Systems formed because of changes in constraint factors and new constraints can no longer satisfy the operation of the systems.
(3 ) Systems formed from changes in both the systems’ own states and their constraints, operating in new conditions and thus making it impossible to determine their laws. Then the systems move in the NO category.
Judging these NO system phenomena, we can see that (1) some have obvious NO conditions and can be identified from observation and analysis of the past operations of the system; (2 ) others are fuzzy NO; people can identify them according to the intrinsic fuzziness of human experiences and reasoning in a system with fuzzy information. They are sets or“ gray NO ( non⁃optimum)” and valuable for system operation decision⁃making and management; (3) potential NO: hidden in the forming stage in a system, has defects in its design but not effecting to functions within certain conditions and its information has not been sensitized.
One rule of scientific research is to develop from the qualitative analysis to the quantitative. To the NOS (non⁃optimum system), if we discuss at certain level of the understanding of its intension. We can analyze quantitatively. Below we’ ll mainly discuss the operating mechanism of NOS in light of the constraint problems.
Suppose the degree of the NO of the system to be
μ
(NO parameter) which is the degree of satisfaction that the system’ s constraints are given by each factor of the system. For example, suppose for a product there exist in number of producing sources
A
i
(
i
= 1,2,…,
m
), each with an output of
a
i
and n number of marketing spots
B
j
(
j
=1,2,…,
n
) each with a sales of
b
j
. If
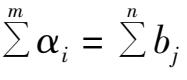 , and unit freight cost from
a
i
to
b
j
is
c
ij
then what distribution plan will ensure the minimum freight cost? This is a typical systematic optimization problem.According to the conventional methods for optimization, it is a process of minimizing the target function while satisfying
, and unit freight cost from
a
i
to
b
j
is
c
ij
then what distribution plan will ensure the minimum freight cost? This is a typical systematic optimization problem.According to the conventional methods for optimization, it is a process of minimizing the target function while satisfying
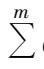 α
i
=
α
i
=
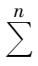 b
j
. Yet in practice, the result of the above process is not the optimum and can not necessarily solve practical problems, mainly because
m
producers and
n
market areas may not make
b
j
. Yet in practice, the result of the above process is not the optimum and can not necessarily solve practical problems, mainly because
m
producers and
n
market areas may not make
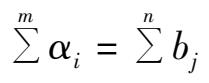 true. Each of the
m
producers and
n
markets has its own satisfaction parameter
μ
i
which can determine the extent that the system optimization accords with the real problem and which are the experiences and quantitative statistics obtained at the starting stage of the system.
true. Each of the
m
producers and
n
markets has its own satisfaction parameter
μ
i
which can determine the extent that the system optimization accords with the real problem and which are the experiences and quantitative statistics obtained at the starting stage of the system.
So the degree of satisfaction of the constraint conditions determines the reciprocal conversions of the NO and O ( optimum) of the system and differentiate the various level system optimization.
Suppose system
U
,
u
i
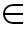 U
(
i
= 1,2,…
m
) has
K
number of constraints
k
(
k
= 1,2,…,
n
). If the satisfaction degree of
u
i
and
K
i
is
μ
i
(
u
i
),then the system’ s degree of NO is
U
(
i
= 1,2,…
m
) has
K
number of constraints
k
(
k
= 1,2,…,
n
). If the satisfaction degree of
u
i
and
K
i
is
μ
i
(
u
i
),then the system’ s degree of NO is
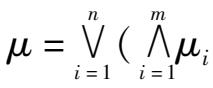 ) where ∨- max; ∧- min
) where ∨- max; ∧- min
To a NOS we can set a value of optimum level
λ
which is the optimum threshold determined by the system and statistical zed and processed. If
λ
= 1, then the SON(system optimization) accords with the reality. If
λ
= 0 the SO doesn’ t accord with reality, that is, the system is not optimized. If
λ
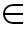 (0,1) then the SON is called satisfactory optimum. For example,
λ
= 0.5 means the system is in a sub⁃optimum(SO) state; if
λ
= 0.7, then the system is at the 0.7 optimum level.
(0,1) then the SON is called satisfactory optimum. For example,
λ
= 0.5 means the system is in a sub⁃optimum(SO) state; if
λ
= 0.7, then the system is at the 0.7 optimum level.
Because the process of SON is cyclic, the system will, after a cycle, get a group of NO degree values which make up the O threshold and NO threshold that is A and A no. The value sets of the NO degree μ can be represented by
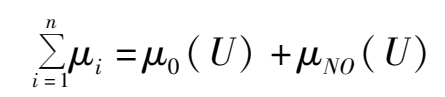
If we can evaluate all the NO parameters of the system, that is, get the O threshold and NO threshold, then we can control the operation of the system and keep it off the NO threshold, thus gaining satisfactory O target.
Models in Nom⁃optimum Systems (NOS),General NO models of complex systems.If the system is clearly NO with clear in formation, then it can definitely be called as“generally NO”.
(1)Common probability model
It is a basic NO system model structured from the values of NO parameters with a certain logic relationships The system calculated and discussed by them all belong to the narrow⁃sensed NO. The methods used for predicting the NOS parameters include those of mathematic calculation: Monte Carlo methods, limit line methods and Boolean logic methods.
(2)Regressive model of NOS
Suppose there are P numbers of constraints whose variables are x 1 , x 2 ,…, x p that shape a NOS from which each constraint and linear interrelating divisors of state variables and constant divisors can be analyzed. Then based on the appearing probability of as few as possible typical constraints x 1 , x 2 ,…, x n we can predict the level and probability of the NO phenomenon. If we let the P 1 , P 2 , P 3 represent the probability of NO phenomenon’ s appearing under n number of constraints combinations, then the interrelatedness between them can be realized by the following regressive model.
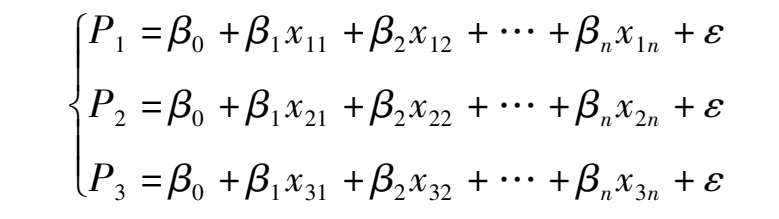
Where
ε
is the error. Now we evaluate the minimum estimate of second multiplication realized by NO
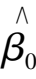 ,
,
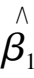 ,…,
,…,
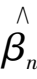 based on observations and statistics of NOS. Thus we can predict the probability of
P
i
level NO realized relative to
x
i
1 +
x
i
2 + …+
x
in
(
i
= 1,2,3)
based on observations and statistics of NOS. Thus we can predict the probability of
P
i
level NO realized relative to
x
i
1 +
x
i
2 + …+
x
in
(
i
= 1,2,3)
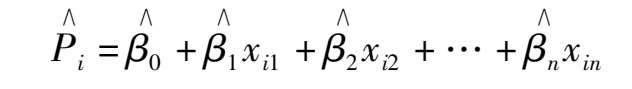
and make it “practical and reliable” following the selection criterion of max
 Lastly,to judge the NO level according to the “principle probability maximum subordination”:
Lastly,to judge the NO level according to the “principle probability maximum subordination”:
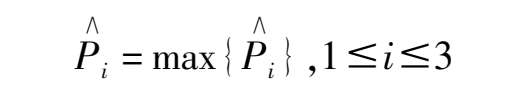
If i = 1, then the system is slightly NO.
If i = 2, then the system is in the category of NO.
If i = 3, then the system is turned into NO state.
(3) Information production model
If the NO state is mainly displayed by some typical monoplane value ( for instance, NO parameter, systerraxcauy shows the tires and kinds of no phenomena),then the prediction of the probability that NO maybe can be performed using the hypothesis of max entropy on the whole. On the other hand, if we know the probability of the appearances of various NO phenomena. We can produce the relationship of the corresponding characteristics.
If the probabilities that the three types of NO show up are
P
1
,
P
2
,
P
3
and
 P
i
=1. We may predict the NOS and evaluate the optimumness utilizing the ratio between the NO parameters,
μ
1
μ
2
,
μ
3
of the three observable characteristic values. According to the methods of information science, we can decide that:
P
i
=1. We may predict the NOS and evaluate the optimumness utilizing the ratio between the NO parameters,
μ
1
μ
2
,
μ
3
of the three observable characteristic values. According to the methods of information science, we can decide that:
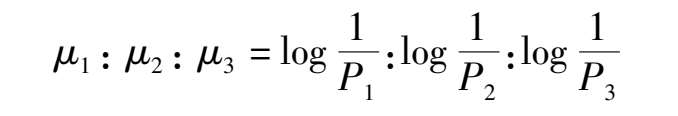
These ratios actually reflect the optimum quality of the system. If we want to calculate the satisfactory operation under limited condones, we can, based upon the above formula relation, produce a group of ratio threshold values, namely, μ 1 : μ 2 = α′ , μ 1 : μ 3 = β′ , μ 2 : μ 3 = γ′ Thus the vectors { α′ , β′ , γ′ } in the Descartes,coordinates will form a space which is called “ optimum space”. Now four typical situations can be identified: when α < α′ , β < β′ , γ < γ′ , the operation of the system is satisfactory and belongs to the optimum category. When α < α′ , β < β′ , γ > γ′ ,the α system operates slightly, tipped toward the optimum category; when α < α′ , β > β′ , γ < γ′ , the system heavily operates in NO; when α > α′ , β > β′ , γ > γ′ , the system is entirely in the state of NO.
The development of human society is forever in the dynamic and uncertainty process of moving from the less ordered toward the more ordered larger system, which is toward its destination point cycle. However we must be aware of the hidden danger under the vigorous stream which may bring about slipped up in decision making and failures. Meanwhile we have already suffered a few slip up in decision making and failures in some areas to some extent. What’ s more failures are that some failures suffered have been repeated and what could have been avoided has not.
From the reliability of the economic reform point of view, we think the most important thing in the Chinese economic reform as a new effort is not a problem of optimizing. Rather, it is one of lessen slipped up in decision making and keeping away failures and detours as possible. Even if some model is considered optimum under the present circumstances, it is hard to be a stable one because it is in the midst of a dynamic process with quite a few hidden threats lurching and many horizontal or vertical sub⁃optimum states. So, if we try to set goals for the economic reform, make plans and take measures and advocate some optimum models simply following the optimum thinking methods out of blind subjective wish, we’ll be actually putting the economic reform on an unreliable and unrealistic basis.
So we say that the non⁃optimum thinking and the methods of non⁃optimum analysis on systems with failure⁃avoiding as its basic aim are based on the non⁃optimum facts with its special ways of thinking, information gathering, analyzing and processing, and with the setting up of non⁃optimum system, these methods seek to lessen slipped up in decision making and failures, thus providing a new way of scientifically summarizing past lesson and making them lamppost for the future. There is profound potential for putting the non⁃optimum thinking into use in Chinas economic reform, and in other country’ s practice. Take the non⁃optimum guiding system for example; it can be employed in the economic reform of the country’ s macro policies, financial system as well as decision analysis. To be sure, the establishment of this non⁃optimum guiding system with computer as its means with information processing techniques as its foundation is no easy task.
The most obvious regulations lie in the economic system. The development degree of a country is shown not only by the change of its economic index. But also by the transit capacity from non⁃optimum to optimum
Because the natures of the systems are different, their border is accordingly different. Of course, the border can change. From the viewpoint of the system’s transit regulation, the border is decided by the structure of the system. For example, the border of the optimum and non⁃optimum of the population system is decided by the synthetically system of the society and the economy. When the population increases to a certain extent, the national economy might keep a certain sustained development, or fluctuate to a certain level. When the population is under control, the national economy might leave the border situation for entering an optimal category. The economic system in the optimal category is called being in an interim. This border is different from the border mentioned before, which reflects that the non⁃optimum attribute is different from the optimal level. Therefore, the border of the economic system and the transit time of the optimum are called the development time of the economic system. However, the aggregate non⁃optimum of the system will be in chaos, and then new attributes come into being, and part of the non⁃optimum of the system will accelerate its selforganization. Therefore, the non⁃optimum behavior and situation of the system contain versatile original dynamic energies, which are excavated, transferred, stored and processed systematically in order to build up the non⁃optimum information system.Actually analysis shows that the advanced format of non⁃optimum information system can be actualized by the hardwares and softwares of the computer; the primary format can be composed of data, documents and diagrams. The primitive energy of the nonoptimum information stored in the systematic database has broken through the limitation of the transit from physical sources to dynamic forces. As long as the states and behaviors of the non⁃optimum information exist, this energy always contains valid combustion value, and can form the dynamic forces accordingly at any time.
From the non⁃optimum analysis theory of systems, it can be concluded that people need the controllable order of the system, and non⁃optimum can also be more orderly.From the non⁃optimum reference system, the transit of the system from non⁃order into order as well as the requisites of the transit can be estimated. The non⁃optimum theory of systems will be widely used in the decision sciences. It can often transform people’s experiences into scientific means and might set up reference models with behavior attributes in the control system. This kind of model can marry the experiences and the theories, and can make actual judges to the running path of the system.
The above is the overall description of the non⁃optimum problem of the system,which tells how to decide the overall frame⁃saw in the non⁃optimum system. However,different measurement and means have to be applied in different systems to solve actual problems. Proper quality and quantity determining methods are applied in the actual system analysis. Furthermore, artificial intelligence and expert system reasoning tools can play important roles in non⁃optimum system analysis.
One of the emphases on the non⁃optimum analysis theory is to describe the borders of the optimum and non⁃optimum category quantitatively. Because the borders change with objective conditions and subjective desire of mankind and human being has different behavior parameters, they always appear as uncertain under dynamic.Meanwhile, because of the continuous progress of mankind’s practice and recognition,under cooperating of the widely exchanged scientific information, the borders might become certain and describable during the dynamic changes. As to the judgment of the reasonability and accountability of the described borders, it is hot a theoretical problem, but a problem of selecting the methods and checking the practice. In addition, when analyzing the problems of the system through quantitative methods, a lot of relationship parameters need to be statistically analyzed and attributably appraised.In many aspects, the influences of the system’s non⁃optimum are depended largely on the experience accumulated in the recognition of the system. That is to say,experiential analysis plays an important role in the non⁃optimum system analysis, which reflects the meaning and function of the combination of the nature and quantity evaluation.
We expect that the non⁃optimum thinking and the methods of non⁃optimum analysis on systems will grow into a new theoretical branch of decision theory that is system non⁃optimum analysis.Meanwhile, applying the theory and methods of information science and system engineering, the non⁃optimum thinking and the methods of non⁃optimum analysis on systems are still in their primitive stage of development and research as a new branch of learning, thinking and theory, But we believe that it will perfect and sophisticate the course of practice and debate, and will bring about results and gain its own position in the world of science.
[1]Simon, H. Models of Discovery. Boston: D. Reidel Pub. Co. ,1977.
[2]Checkland P B. Systems Thinking, Systems Practice M. John Wiley & Sons Ltd. , Chichester,UK,1981,262-278.
[3]Checkland P B. Systems Thinking, Systems Practice. John Wiley & Sons Ltd. , Chichester ,UK,1981,12,16,18.
[4] Simon, H. A Behavioral Model of Rational Choice. In H. Simon ( Ed. ), Models of Bounded Rationality, Behavioral Economics and Business Organization, Cambridge, MA:MIT Press,1982, vol. 2,pp. 239-258.
[5]Simon, H. The Science of the Artificial, The MI Press, 2nd edition,1982,68, pp. 100-168.
[6]Ping He. System Non⁃optimum Analysis and Extension Optimum Theory. In: Guangya Chen,ed, Proc. of the International conference on Systems Science and Systems Engineering,2003,pp. 131-137.
[7]Linstone H, Multiple Perspectives for Decision Making, New York: North Holland Publishing,1984,pp.10-17.
系统工程
1989,7(2):1-5