




摘 要 : 本文对具有某些代数曲面解的具有常收获率和常投放率的三种群 Volterra 模型在 R 3 + 内的相图进行了分析 , 并举出了一些具体例子 .
关键词 : 三种群 Volterra 模型 , 收获率 , 投放率 , 相图
三维系统的相图要比二维系统的相图复杂得多,对于二维系统相图的分析虽然也不是太容易,但其已有的成果可以说已不胜枚举.而对于三维系统的相图分析却很少见.
其主要原因是难度太大,对于一些实际问题的具体三维系统模型,在
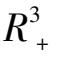 (第一卦限)内极限环的存在性、唯一性,或平衡点的稳定性全局稳定性等,虽然也有过不少结果.例如极限环存在性方面的结果如文〔1,2〕等,平衡点稳定性,或全局稳定的如文〔3,4〕等,但是在
(第一卦限)内极限环的存在性、唯一性,或平衡点的稳定性全局稳定性等,虽然也有过不少结果.例如极限环存在性方面的结果如文〔1,2〕等,平衡点稳定性,或全局稳定的如文〔3,4〕等,但是在
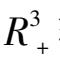 轨线的分布与走向状况却知之甚少,而
轨线的分布与走向状况却知之甚少,而
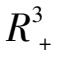 内轨线分布和走向恰恰是解决实际问题时所最需要的.比如对给的初始点,那些变元最终走向灭绝,那些变元始终保持存在,且将稳定在什么位置上,这些都正是实际所最需要加以解决的问题.
内轨线分布和走向恰恰是解决实际问题时所最需要的.比如对给的初始点,那些变元最终走向灭绝,那些变元始终保持存在,且将稳定在什么位置上,这些都正是实际所最需要加以解决的问题.
文〔5〕曾证明过系统:
 =
x
(1-
x
-
αy
-
βNz
) +
ε
,
=
x
(1-
x
-
αy
-
βNz
) +
ε
,
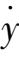 =
y
(1 +
βx
-
y
-
az
) +
ε
,
=
y
(1 +
βx
-
y
-
az
) +
ε
,
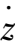 =
z
(1-
αx
-
βy
-
z
) +
ε
=
z
(1-
αx
-
βy
-
z
) +
ε
在满足一定条件时存在极限环,但极限环的可能形状,区域 R 3 +内轨线的可能分布和走向方面仍一无所知.本文将考虑以下系统
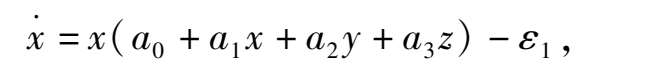

并试图探索此类系统在
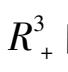 内轨线可能的分布和走向.当然对一般情况下的系统(1),要较全面地解决此问题难度很大,简直无法下手.所以现在我们只研究当系统(1)具有某些代数曲面解时的特殊情形.因为这时我们就有可能将此三维系统转化为二维系统来进行研究.尽管对这类特殊的系统(1)轨线的研究结果不能代表一般的系统(1),但至少可以知道系统(1)的轨线可以出现何种类型的拓扑结构.也可以为进一步对一般的系统(1)的研究提供线索和信息.
内轨线可能的分布和走向.当然对一般情况下的系统(1),要较全面地解决此问题难度很大,简直无法下手.所以现在我们只研究当系统(1)具有某些代数曲面解时的特殊情形.因为这时我们就有可能将此三维系统转化为二维系统来进行研究.尽管对这类特殊的系统(1)轨线的研究结果不能代表一般的系统(1),但至少可以知道系统(1)的轨线可以出现何种类型的拓扑结构.也可以为进一步对一般的系统(1)的研究提供线索和信息.
我们有以下定理:
定理 1 系统(1)具有平面解 F ( x , y , z ) = x + y + z -1 = 0 的充要条件是此系统可表示成以下形式:
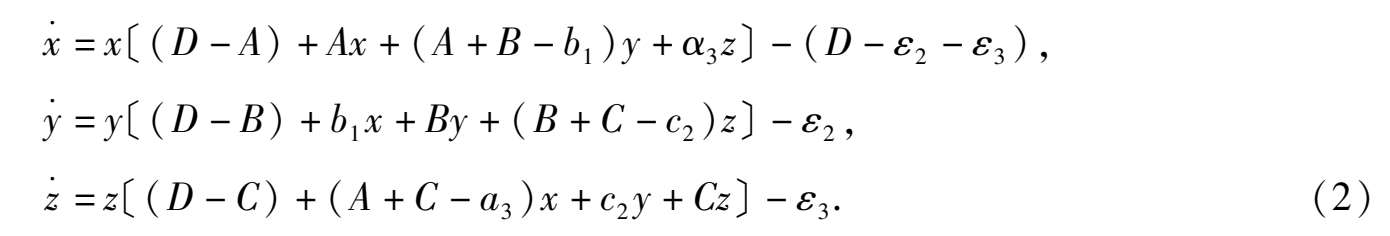
这里 A , B , C , b 1 , a 3 , c 2 均为任意常数, D = ε 1 + ε 2 + ε 3 .
证 设系统(1)具有平面解 F ( x , y , z ) = x + y + z -1 = 0,则对系统(1)有
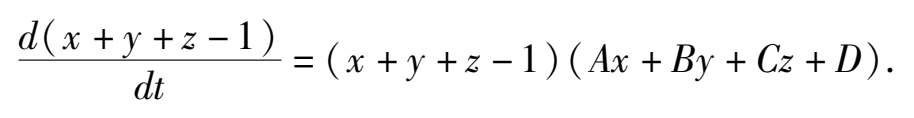
即
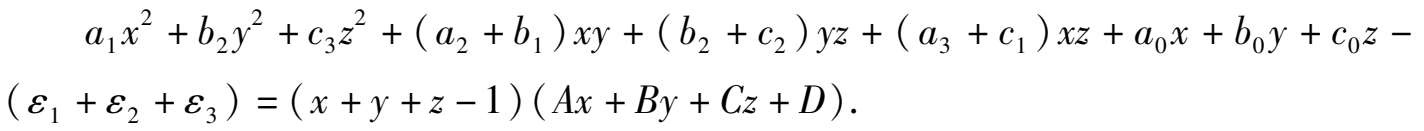
比较系数得:
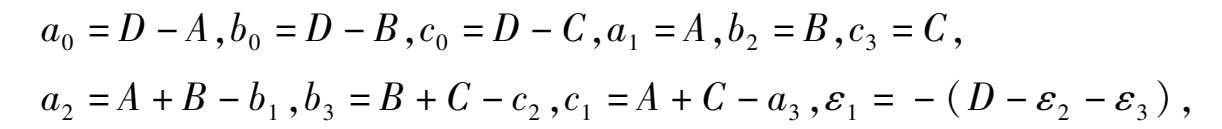
代入系统(1)即得系统(2).条件的充分性证毕.条件的必要性是显然的.证毕.
我们假设系统(2)的三种群都具有正出生率,不妨都设为 1,即设 D - A = 1, D - B = 1, D - C = 1,则系统(2)变成以下形式:
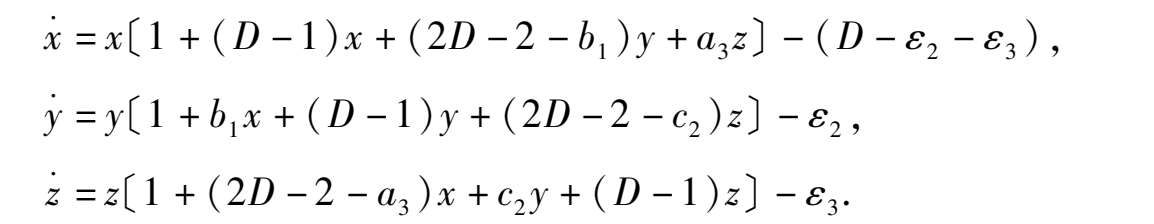
因三种群的密谋制约项必为负,所以可设 D -1 =- α ( α > 0).并记 b 1 =- γ , c 2 =- δ , α 3 =- β ,于是此系统又可写成:
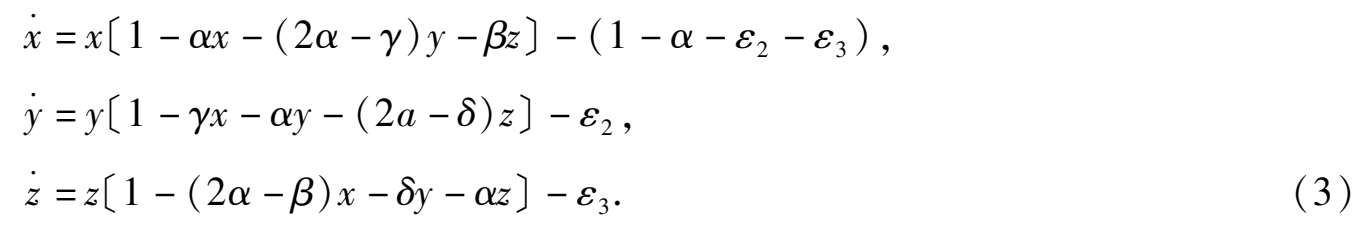
因为
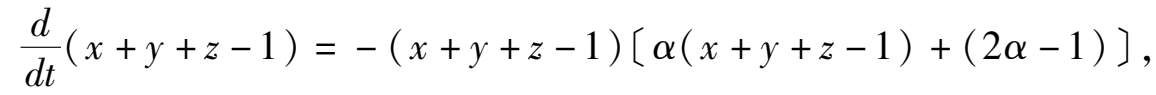
系统(3)有初积分为:
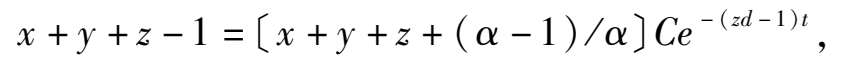
其中 C 是任意常数.
引理
1 系统(3)在第一卦限
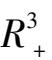 是有界系统.
是有界系统.
证
因
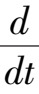 (
x
+
y
+
z
-
N
) =-(
x
+
y
+
z
-1)〔
α
(
x
+
y
+
z
-1)+ (2
α
-1)〕,
(
x
+
y
+
z
-
N
) =-(
x
+
y
+
z
-1)〔
α
(
x
+
y
+
z
-1)+ (2
α
-1)〕,
所以
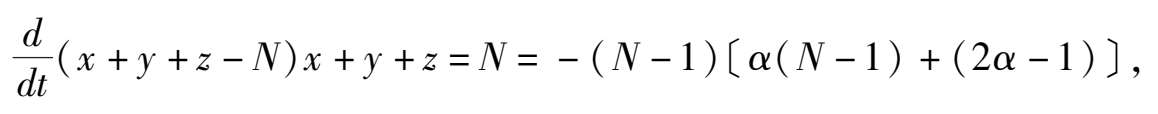
当
N
充分大时
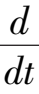 (
x
+
y
+
z
-
N
)
x
+
y
+
z
=
N
< 0,证毕.
(
x
+
y
+
z
-
N
)
x
+
y
+
z
=
N
< 0,证毕.
引理 2 系统(3)
当0 <
α
<
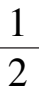 时,
时,
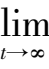 (
x
+
y
+
z
) =-
(
x
+
y
+
z
) =-
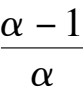 ,
,
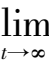 (
x
+
y
+
z
) = 1,
(
x
+
y
+
z
) = 1,
当
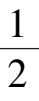 ≤
α
< 1 时,
≤
α
< 1 时,
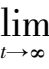 (
x
+
y
+
z
) = 1,
(
x
+
y
+
z
) = 1,
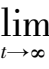 (
x
+
y
+
z
) =-
(
x
+
y
+
z
) =-
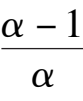 ,
,
当
α
> 1 时,
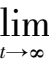 (
x
+
y
+
z
) = 1.
(
x
+
y
+
z
) = 1.
证明略.
引理 2 说明系统(3)有两个平行面解,即平面解Ⅰ:
x
+
y
+
z
= 1,和平面解Ⅱ:
x
+
y
+
z
+
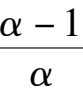 = 0,当0 <
α
<
= 0,当0 <
α
<
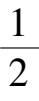 时,Ⅰ是负向不变集;Ⅱ是正向不变集,当
时,Ⅰ是负向不变集;Ⅱ是正向不变集,当
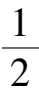 <
α
<1时,则反之.当
α
> 1时Ⅰ是正向不变集.当
α
=
<
α
<1时,则反之.当
α
> 1时Ⅰ是正向不变集.当
α
=
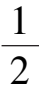 时,Ⅰ与Ⅱ重合,这时面向原点的一侧属负向不变集,背向原点的一侧属正向不变集.
时,Ⅰ与Ⅱ重合,这时面向原点的一侧属负向不变集,背向原点的一侧属正向不变集.
对系统(3)设 x = 1- y - x 得
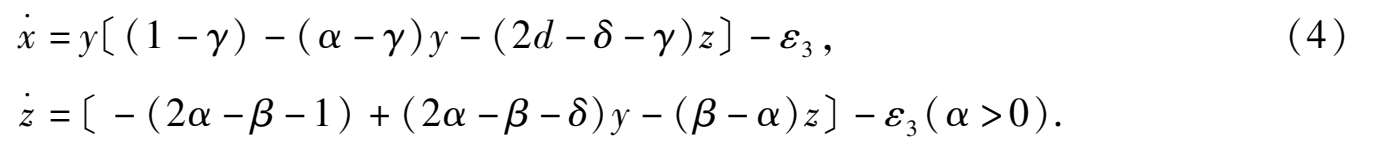
这是关于
y
,
z
均具有常收获或常投放的Volterra系统.如对系统(3)作变换
x
=-
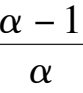 -
y
-
z
得
-
y
-
z
得
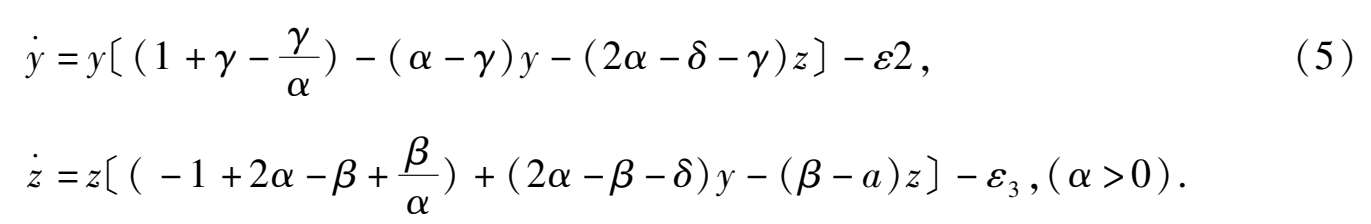
这也是关于 y , z 均具常收获或常投放的Volterra系统.
如果我们能得出系统(4)和(5)在平面(
y
,
z
)上第一象限内的相图,那么根据引理 2,我们就不难得知系统(3)在
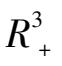 内轨线分布和走向状况.二维系统(4)和(5)是可以存在极限环的,从而可知三维系统(3)也是可以存在极限环的.但是仅靠定性的方法要对一般的系统(4)和(5)给出它们丰在极限环的精确条件,难度是极大的,如果要进一步研究系统(4)和(5)的在第一象限内各种可能的轨线的拓朴结构,难度更大.由于我们现在不想纠缠在对一般二维系统(4)与(5)的冗长的讨论上,所以本文只想举一些具体的数字系统的例子来说明三维系统(3)在
内轨线分布和走向状况.二维系统(4)和(5)是可以存在极限环的,从而可知三维系统(3)也是可以存在极限环的.但是仅靠定性的方法要对一般的系统(4)和(5)给出它们丰在极限环的精确条件,难度是极大的,如果要进一步研究系统(4)和(5)的在第一象限内各种可能的轨线的拓朴结构,难度更大.由于我们现在不想纠缠在对一般二维系统(4)与(5)的冗长的讨论上,所以本文只想举一些具体的数字系统的例子来说明三维系统(3)在
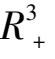 内可能出现的轨线分布和走向.这对进一步揭示系统(3)的轨线结构是有益的.
内可能出现的轨线分布和走向.这对进一步揭示系统(3)的轨线结构是有益的.
例
1令
α
= 2,
β
= 2,
δ
=-1,
γ
=-6,
ε
1
=
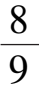 ε
3
= 0,
这时系统(3)形为
ε
3
= 0,
这时系统(3)形为

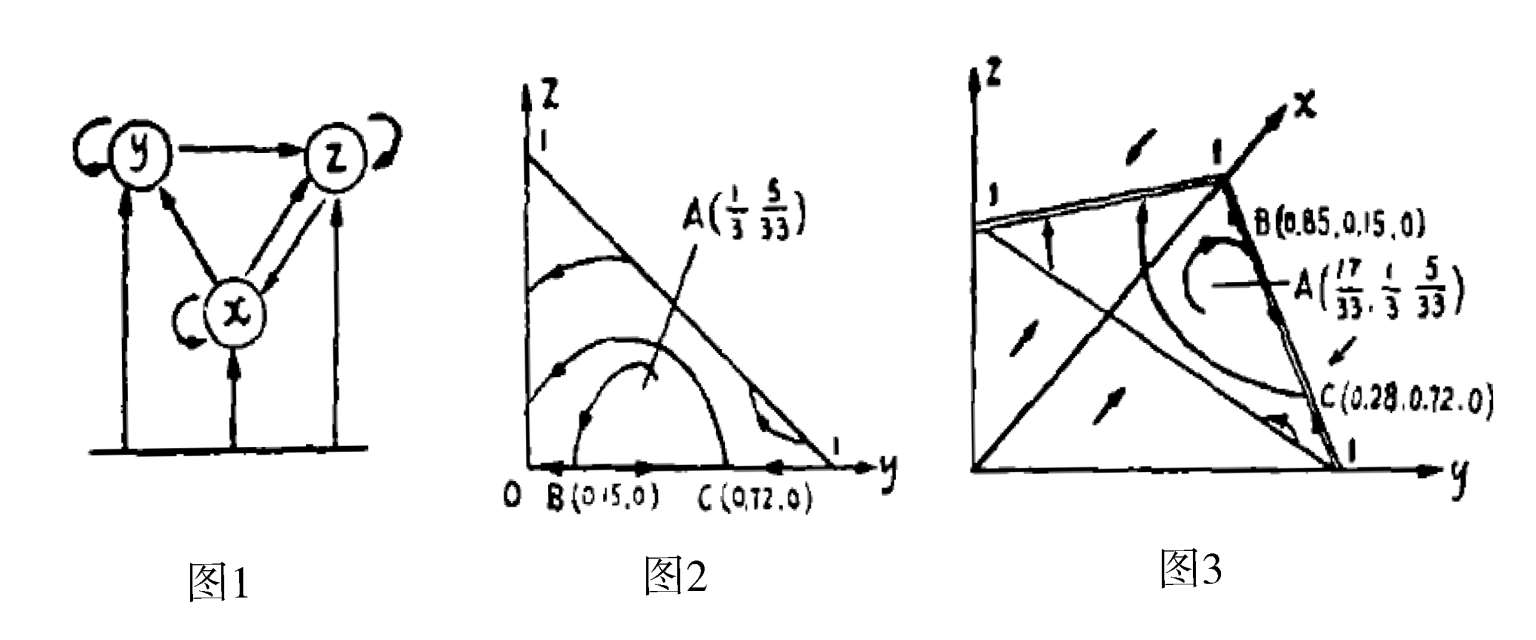
系统(6)中的种群 x , y , z 之间的关系如图 1 所示,其中对 x 有常投放,对 y 有常收获.系统(6)通过变换 x = 1- y - z 得二维系统(4)形如

系统(7)在第一象限有唯一奇点
A
(
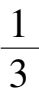 ,
,
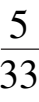 ),它位于区域
D
:{(
y
,
z
) |
y
> 0,
z
>0,
y
+
z
< 1}内.且易验知
A
为系统(7)的一阶不稳定细焦点.系统(7)在第一象限内的相图如图2 所示.因
α
> 1,从引理2 知系统(6)在
),它位于区域
D
:{(
y
,
z
) |
y
> 0,
z
>0,
y
+
z
< 1}内.且易验知
A
为系统(7)的一阶不稳定细焦点.系统(7)在第一象限内的相图如图2 所示.因
α
> 1,从引理2 知系统(6)在
 的轨线当
t
→∞时均趋向于平面解
x
+
y
+
z
-1 = 0,所以系统(6)在
的轨线当
t
→∞时均趋向于平面解
x
+
y
+
z
-1 = 0,所以系统(6)在
 内轨线的分布和走向大致如图 3所示.
内轨线的分布和走向大致如图 3所示.
如在系统(6)的基础上令
ε
2
减小,即令
α
= 2,
β
= 2,
δ
=-1,
γ
=-6,
ε
2
=
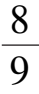 -
Δε
2
(0 <
Δε
2
< 1)则系统(6)和系统(7)分别变成
-
Δε
2
(0 <
Δε
2
< 1)则系统(6)和系统(7)分别变成
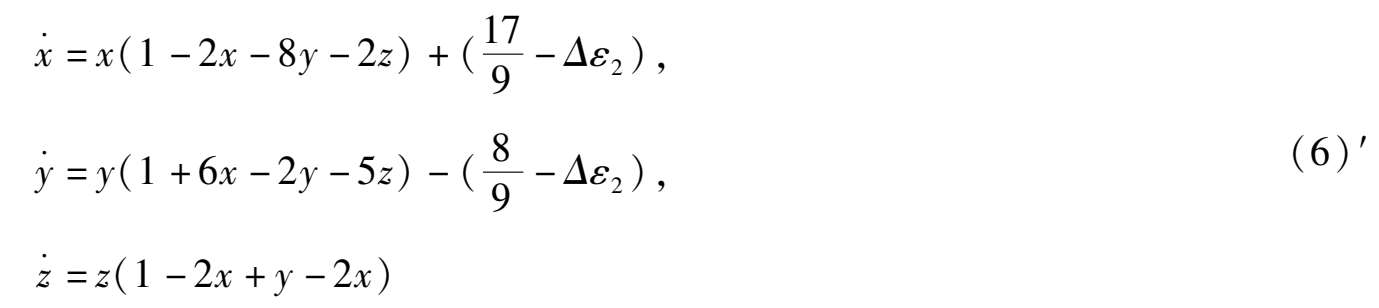
和
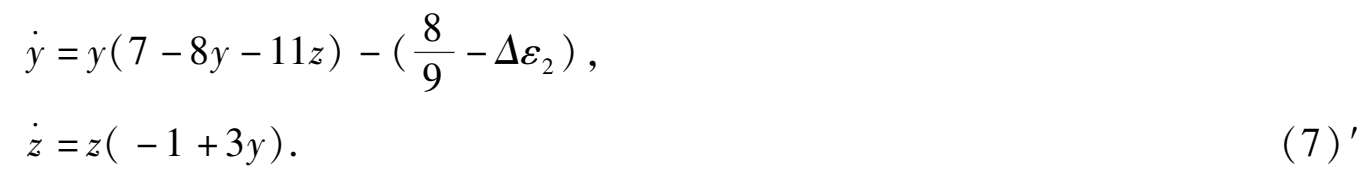
由于这时系统(7)′在第一象限的唯一奇点
A
(
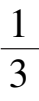 ,
,
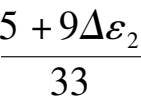 )变成稳定粗焦点,所以
A
外围出现了一个不稳定极限环.其相图变成图 4 所示.从而系统(6)′在
)变成稳定粗焦点,所以
A
外围出现了一个不稳定极限环.其相图变成图 4 所示.从而系统(6)′在
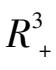 也出现了唯一不稳定极限环,它位于平面解
x
+
y
+
z
-1 = 0 上.如图 5 所示.
也出现了唯一不稳定极限环,它位于平面解
x
+
y
+
z
-1 = 0 上.如图 5 所示.
注
1 在系统(7)′和(6)′中,当 0 <
Δε
2
< 1 时极限环存在(唯一),不必一定限制
Δε
2
为充分小,实际上当
Δε
2
增大到
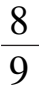 时,系统(7)′在第一象限将全局稳定于点
A
(
时,系统(7)′在第一象限将全局稳定于点
A
(
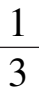 ,
,
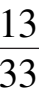 ).所以在间向0<
Δε
2
<
).所以在间向0<
Δε
2
<
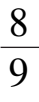 必存在使得系统(7)′在
A
外围存在弓形分界线环的值.由于系统(7)′对
Δε
2
不构成旋转向量场,所以这个值不是唯一的.如设其中最小的值为
Δε
2
,则当 0 <
Δε
2
<
Δε
2
时,系统(7)′必存在(唯一)不稳定极限环,从而系统(6)′也存在(唯一)不稳定极限环.
必存在使得系统(7)′在
A
外围存在弓形分界线环的值.由于系统(7)′对
Δε
2
不构成旋转向量场,所以这个值不是唯一的.如设其中最小的值为
Δε
2
,则当 0 <
Δε
2
<
Δε
2
时,系统(7)′必存在(唯一)不稳定极限环,从而系统(6)′也存在(唯一)不稳定极限环.
注 2 系统(6)′当 0 < Δε 2 < Δε 2 时的不稳定极限环位于平面 x + y + z -1 = 0 上完全有可能与图 5 中的线段 RQ 相交,也即沿某一轨线,当 t 到达某一有限时刻,种群 x 就灭绝了,但后又复生了,这不足为奇,因为 x 具有常投放率.
注
3 系统(6)′当
Δε
2
减小时,种群
x
,
y
,
z
不能共存,当
t
到达某有限时刻,
y
必灭绝,只剩下
x
和
z
,而当
Δε
2
增大时,
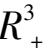 内将出现稳定区域,即出现
x
,
y
,
z
共存的区域.当
Δε
2
增大到
内将出现稳定区域,即出现
x
,
y
,
z
共存的区域.当
Δε
2
增大到
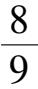 时,
时,
 内全局稳定于点
内全局稳定于点
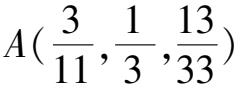 .
.
例
2令
α
=
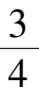 ,
δ
=
,
δ
=
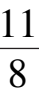 ,
β
=
,
β
=
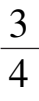 ,
γ
=-8,
ε
2
=
,
γ
=-8,
ε
2
=
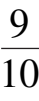 ,
ε
2
= 0,这时系统(3)形为
,
ε
2
= 0,这时系统(3)形为
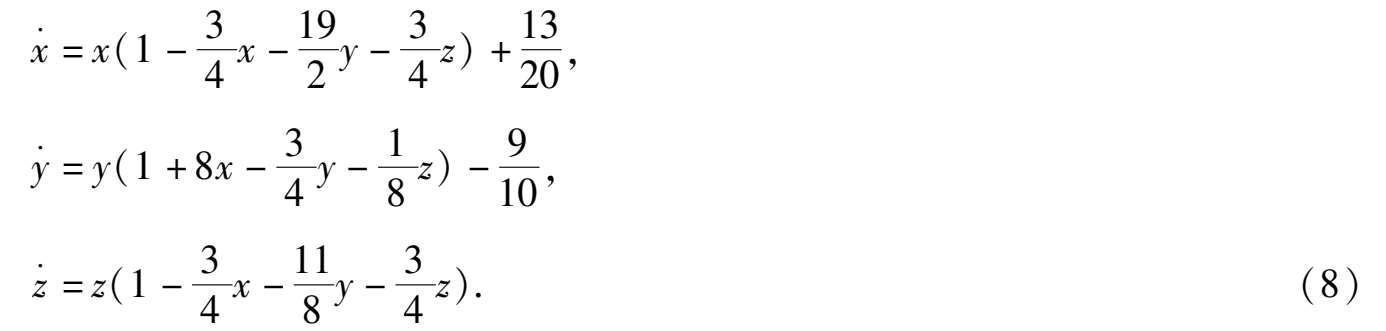
系统(8)中的种群 x , y , z 之间的关系如图 6 所示,对 x 有常设放,对 y 有常收获.系统(8)通过变换 x = 1- y - z 所得系统(4)形为

系统(9)在第一象限有唯一奇点
A
(
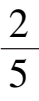 ,
,
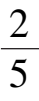 ),它位于区域
D
:{(
y
,
z
) |
y
> 0,
z
>0
y
+
z
< 1}内,
y
轴上有奇点
B
(
),它位于区域
D
:{(
y
,
z
) |
y
> 0,
z
>0
y
+
z
< 1}内,
y
轴上有奇点
B
(
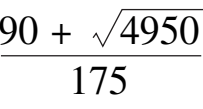 ,0)=
B
(0.916,0)和
C
(
,0)=
B
(0.916,0)和
C
(
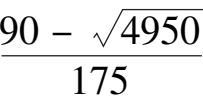 ,0)=
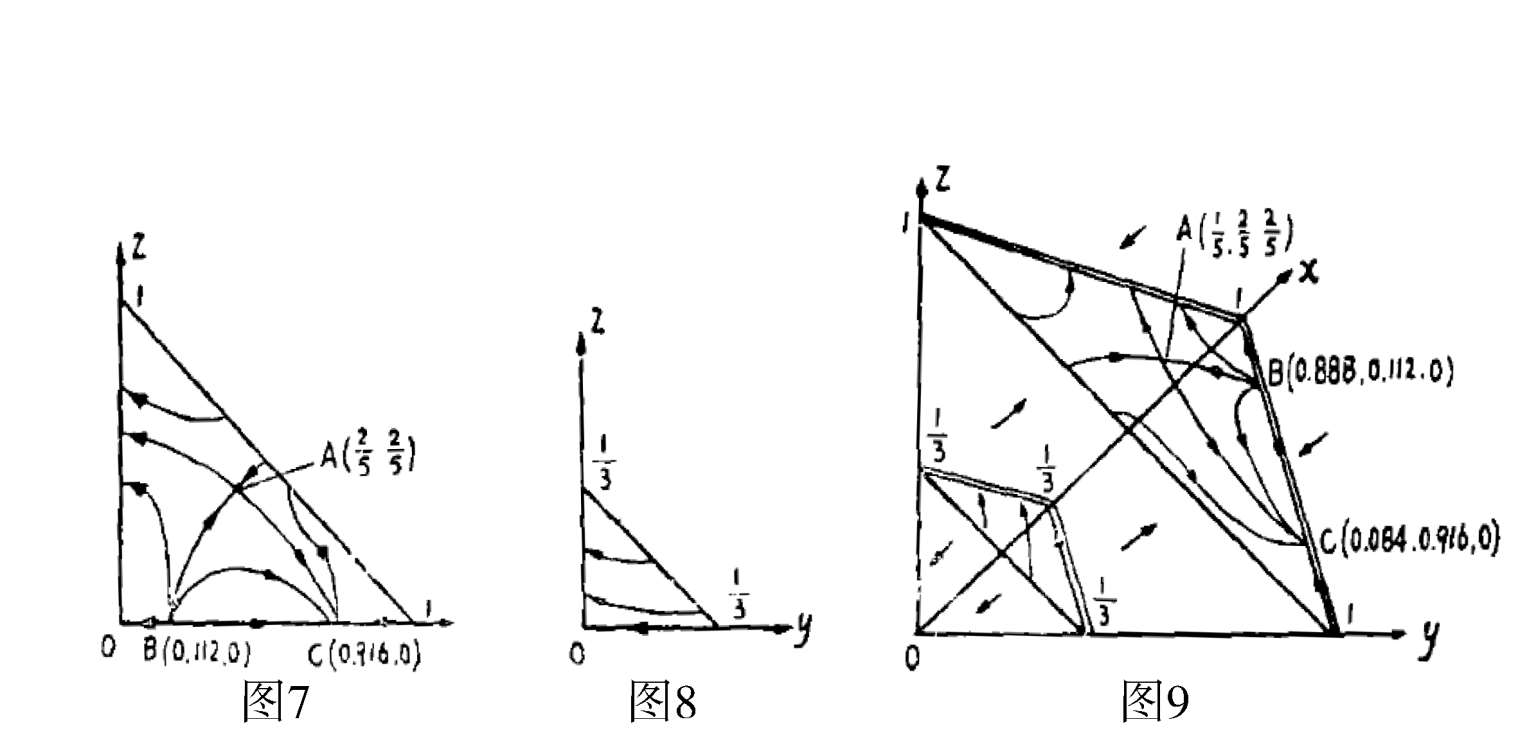
C
(0,112,0)
A
为鞍点,
B
为稳定结点,
C
为不稳定结点.系统(9)在第一象限的相图如图 7 所示.
,0)=
C
(0,112,0)
A
为鞍点,
B
为稳定结点,
C
为不稳定结点.系统(9)在第一象限的相图如图 7 所示.
系统(8)通过变换
x
=
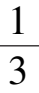 -
y
-
z
所得系统(5)形为
-
y
-
z
所得系统(5)形为
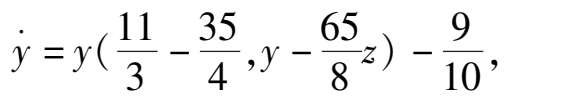

系统(10)全平面只有唯一奇点
A
(
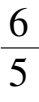 ,-
,-
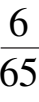 ),在第一象限相图如图 8 所示.
),在第一象限相图如图 8 所示.
因
a
=
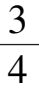 < 1,所以由引理 1 可知系统(8)的平面
x
+
y
+
z
-1 = 0 是正向不变集,平面
x
+
y
+
z
-
< 1,所以由引理 1 可知系统(8)的平面
x
+
y
+
z
-1 = 0 是正向不变集,平面
x
+
y
+
z
-
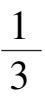 = 0是负向不变集.所以系统(8)在
= 0是负向不变集.所以系统(8)在
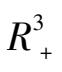 的相图如图 9 所示.在
的相图如图 9 所示.在
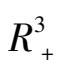 内,平面I:
x
+
y
+
z
= 1 上侧轨线均走向平面I;在平面I和Ⅱ:
x
+
y
+
z
=
内,平面I:
x
+
y
+
z
= 1 上侧轨线均走向平面I;在平面I和Ⅱ:
x
+
y
+
z
=
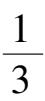 之间,轨线均远离Ⅱ而走向Ⅰ;在平面Ⅱ下侧轨线均远离Ⅱ.
之间,轨线均远离Ⅱ而走向Ⅰ;在平面Ⅱ下侧轨线均远离Ⅱ.
注 4 系统(8)中种群 x , y , z 不能共存,根据初始点( x 0 , y 0 , z 0 )所在的位置,有以下几种不同的结果:
1)如初始点(
x
0
,
y
0
,
z
0
)位于平面Ⅱ的上侧时有两种可能性:一种是当
t
→ + ∞时,
z
灭绝,而
x
和
y
的数量稳定在(0.084,0.916);另一种是当
t
到达有限时刻
y
将灭绝而
x
,
z
仍存在着.例如当0 <
δ
≪1时初始点取在(
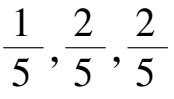 +
δ
)时,
y
必当
t
于有限时刻就灭绝,
x
,
z
存在;初始点取在(
+
δ
)时,
y
必当
t
于有限时刻就灭绝,
x
,
z
存在;初始点取在(
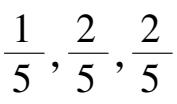 -
δ
)时,当
t
→∞时,
z
灭绝,而
x
,
y
稳定在(0.084,0.916),初始点位置差以毫厘,后果却不大一样.
-
δ
)时,当
t
→∞时,
z
灭绝,而
x
,
y
稳定在(0.084,0.916),初始点位置差以毫厘,后果却不大一样.
2)如初始点( x 0 , y 0 , z 0 )位于平面Ⅰ的下侧.则当 t 到达有限时刻时 y 必灭绝,而 x , z 继续存在.
以上我们只举了两个例子,如果对于系统(3)任意给定
α
,
β
,
γ
,
δ
,
ε
2
,
ε
3
的一组数,我们都可以描绘出所对应的系统(3)在
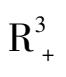 内的轨线分布图.至于对系统(3)的一般性讨论,有待进一步研究.
内的轨线分布图.至于对系统(3)的一般性讨论,有待进一步研究.
参考文献
[1]Lo Sheag Dai,Noncoustant periodic solution in predatorprey systems with continuous time delay,Math,Biosci,53,1981,109-157.
[2]Gopalsamy,K. Aggarwala B. D. ,Limit cycles in two species competition with time delays,J. Aust Math Soc. Ser. B. 1980,21,148-160.
[3]Bowads J. M. and Cushing J. M. ,On the behavior of sofutions of predator- prey equations with bereditary term,Math,Biosci,1975,29,41-54.
[4]陈兰荪,数学生态模型与研究方法,科学出版社,北京,1988,310-321,205-232.
[5] Grusman W,Periodic solutions of autonomous differential equations in higher dimeasion spaces Rocky Mountain J. Math. 1977,7(3):457-466.
[6]陈兰荪,数学生态模型与研究方法,科学出版社,北京,1988,310-321,205-232.
Abstract :This paper presents the analysis of the phase portrait of three species Volterra model with the rates of constant harvest and constant invest braic curved surface solution in R 3 +It also offers some practical examples.
Keywords :Three species Volterra model,Harvest rate,Invest rate,Phase portrait.
应用数学学报
1994,17(4):592-596