




针对式(3.2.1)和式(3.2.2)描述的系统,基于假设3.2.1~假设3.2.4,设计如下形式的滤波器:
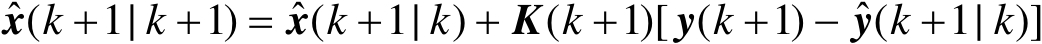
(3.3.1)
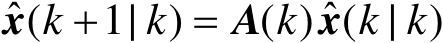
(3.3.2)
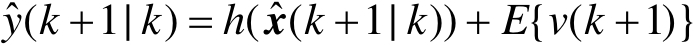
(3.3.3)
其中, K ( k +1)∈ R n ×1 为一个待设计的特征函数滤波器增益向量, K ( k +1) 的获取是整个滤波器设计的核心与关键。
基于式(3.2.8)对估计误差的定义,由式(3.3.1)及状态 x ( k +1) 的估计误差定义,可得状态 x ( k +1) 估计误差的传播方程为
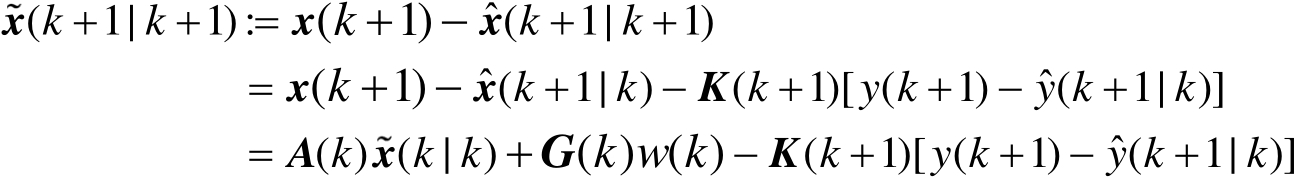
(3.3.4)
Guo和Wang在文献[17]中指出,当
A
(
k
)、
G
(
k
)、
y
(
k
+1)、
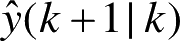 及
K
(
k
+1) 给定时,
及
K
(
k
+1) 给定时,
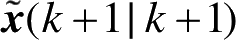 就可以用
就可以用
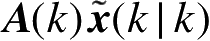 与
G
(
k
)
w
(
k
) 这两个独立的向量,以及一个测量误差项
与
G
(
k
)
w
(
k
) 这两个独立的向量,以及一个测量误差项
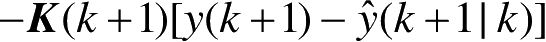 来表示。所以,在已知
A
(
k
)、
G
(
k
)、
y
(
k
+1)、
来表示。所以,在已知
A
(
k
)、
G
(
k
)、
y
(
k
+1)、
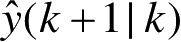 及
K
(
k
+1) 的情况下,
及
K
(
k
+1) 的情况下,
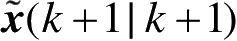 的概率密度函数就是基于
的概率密度函数就是基于
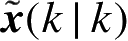 与
w
(
k
) 的概率密度函数的综合概率密度函数。
与
w
(
k
) 的概率密度函数的综合概率密度函数。