




定义2.5
时标
 是实数集
是实数集
 的一个非空闭子集,它遗传了
的一个非空闭子集,它遗传了
 上的拓扑和序结构。
上的拓扑和序结构。
定义2.6
前跃算子
σ
:
 →
→
 定义为:
定义为:
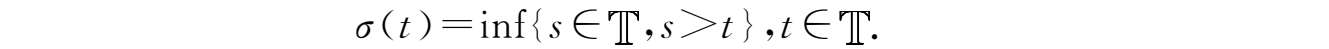
后跃算子
ρ
:
 →
→
 定义为:
定义为:
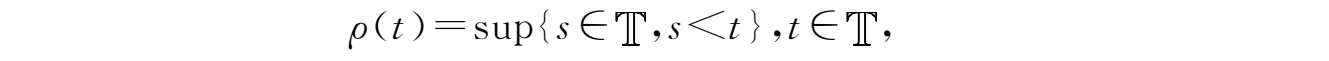
规定inf∅=sup
 ,sup∅=inf
,sup∅=inf
 。
。
定义2.7
粗细度函数
μ
:
 →[0,∞)定义为:
→[0,∞)定义为:
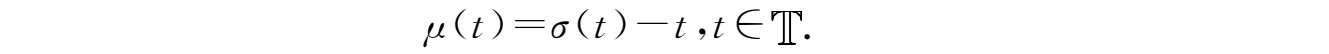
称满足
t
>inf
 且
ρ
(
t
)=
t
的点
t
∈
且
ρ
(
t
)=
t
的点
t
∈
 是左稠的;称满足
ρ
(
t
)<
t
的点
t
∈
是左稠的;称满足
ρ
(
t
)<
t
的点
t
∈
 为左离散的;称满足
t
<sup
为左离散的;称满足
t
<sup
 且
σ
(
t
)=
t
的点
t
∈
且
σ
(
t
)=
t
的点
t
∈
 是右稠的;称满足
ρ
(
t
)>
t
的点
t
∈
是右稠的;称满足
ρ
(
t
)>
t
的点
t
∈
 为右离散的。
为右离散的。
定义2.8
若
 有一个左离散的最大值
m
,则
有一个左离散的最大值
m
,则
 k
=
k
=
 \{
m
},否则
\{
m
},否则
 k
=
k
=
 ;若
;若
 有一个右离散的最小值
m
,则
有一个右离散的最小值
m
,则
 k
=
k
=
 \{
m
},否则
\{
m
},否则
 k
=
k
=
 。
。
定义2.9
若对函数
f
:
 →
→
 ,
t
∈
,
t
∈
 k
,
f
Δ
(
t
)满足以下条件:对任意
ε
>0,存在
t
的邻域
U
,使得
k
,
f
Δ
(
t
)满足以下条件:对任意
ε
>0,存在
t
的邻域
U
,使得
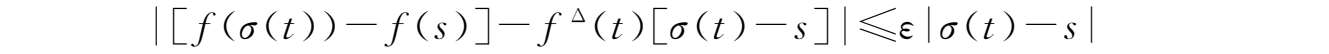
对所有 s ∈ U 成立,则称 f Δ ( t )为 f ( t )的Delta导数。
定义2.10
设函数
z=
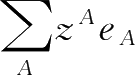 :
:
 →
→
 ,其中
z
A
:
,其中
z
A
:
 →
→
 ,若对任意的
A
∈
Λ
,(
z
A
)
Δ
(
t
)存在,则称
z
Δ
(
t
)
=
,若对任意的
A
∈
Λ
,(
z
A
)
Δ
(
t
)存在,则称
z
Δ
(
t
)
=
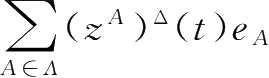 为Clifford数
z
的Delta导数。
为Clifford数
z
的Delta导数。
定
义
2.11设函数
z=
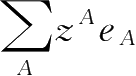 :
:
 →
→
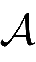 ,其中
z
A
:
,其中
z
A
:
 →
→
 ,若对任意的
A
∈
Λ
,
z
A
是右稠连续的,则称
,若对任意的
A
∈
Λ
,
z
A
是右稠连续的,则称
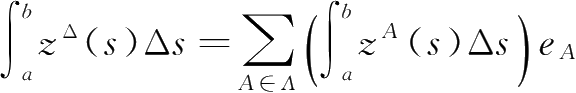 为Clifford数
z
从
a
到
b
的Delta积分。
为Clifford数
z
从
a
到
b
的Delta积分。
引理2.1
若
f
:
 →
→
 ,且
t
∈
,且
t
∈
 k
.则
k
.则
①若 f 连续,则 f 右稠连续。若 f 在 t 处可微,则 f 在 t 处连续;
②若 f 在 t 处连续且 t 是右离散的,则 f 在 t 处可微,且
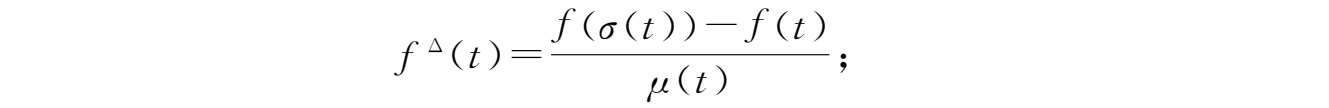
③若
t
是右稠密的,则
f
在
t
处可微当且仅当极限
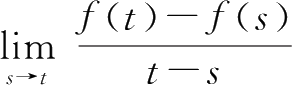 存在。即
存在。即
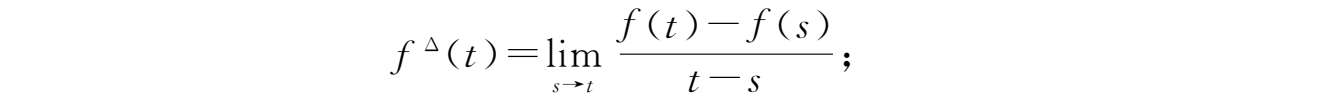
④若 f 在 t 处可微,则 f ( σ ( t ))= f ( t )+ μ ( t ) f Δ ( t )。
引理2.2
若
f
,
g
:
 →
→
 在
t
∈
在
t
∈
 k
处可微,则有下列结论成立:
k
处可微,则有下列结论成立:
①对任意常数
α
,
β
,(
αf
+
βg
):
 →
→
 ,在
t
处可微且(
αf
+
βg
)
Δ
(
t
)=
αf
Δ
(
t
)+
βg
Δ
(
t
);
,在
t
处可微且(
αf
+
βg
)
Δ
(
t
)=
αf
Δ
(
t
)+
βg
Δ
(
t
);
②积
fg
:
 →
→
 在
t
处可微且
在
t
处可微且
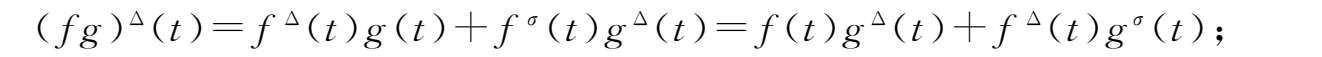
③若
g
(
t
)
g
σ
(
t
)≠0,则
 :
:
 →
→
 在
t
处可微且
在
t
处可微且
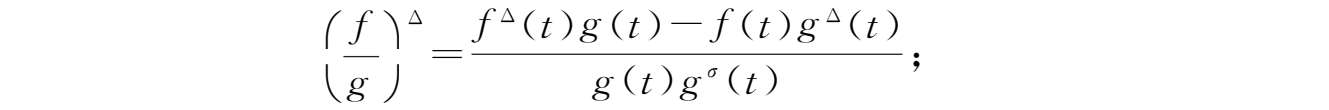
④若
f
和
f
Δ
连续,则
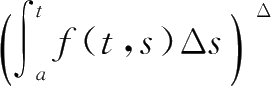 =f
(
σ
(
t
),
t
)
+
=f
(
σ
(
t
),
t
)
+
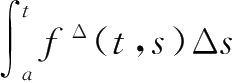
定义2.12
若函数
f
:
 →
→
 在
在
 中的右稠点的右极限存在且左稠点的左极限存在,则称其为正则的。
中的右稠点的右极限存在且左稠点的左极限存在,则称其为正则的。
定义2.13
若函数
f
:
 →
→
 在
在
 中的右稠点处连续且在左稠点的左极限存在,则称其为右稠连续的。记
C
rd
(
中的右稠点处连续且在左稠点的左极限存在,则称其为右稠连续的。记
C
rd
(
 ,
,
 ):={
f
|
f
:
):={
f
|
f
:
 →
→
 右稠连续},简记为
C
rd
(
右稠连续},简记为
C
rd
(
 )或
C
rd
.
)或
C
rd
.
定义2.14
设
f
为右稠连续的,若
F
Δ
(
t
)=
f
(
t
),则(1)若对任意
a
,
t
∈
 ,有
,有
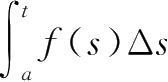 =F
(
t
)
-F
(
a
)成立,则称
=F
(
t
)
-F
(
a
)成立,则称
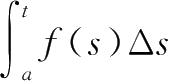 为
f
的
Δ
积分;(2)若对任意
为
f
的
Δ
积分;(2)若对任意
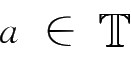 ,
,
 ,
ρ
(
t
)≥
a
,有
,
ρ
(
t
)≥
a
,有
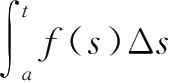 =F
(
ρ
(
t
))
-F
(
a
)成立,则称
=F
(
ρ
(
t
))
-F
(
a
)成立,则称
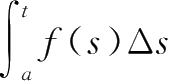 为
f
的
Δ
积分;(3)若对任意
为
f
的
Δ
积分;(3)若对任意
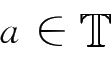 ,
t
∉
,
t
∉
 ,
σ
(
t
)≤
a
,有
,
σ
(
t
)≤
a
,有
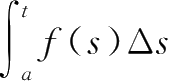 =
F
(
σ
(
t
))
-F
(
a
)成立,则称
=
F
(
σ
(
t
))
-F
(
a
)成立,则称
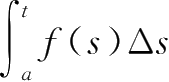 为
f
的
Δ
积分。
为
f
的
Δ
积分。
引理2.3
若
f
∈
C
rd
且
t
∈
 k
,则
k
,则
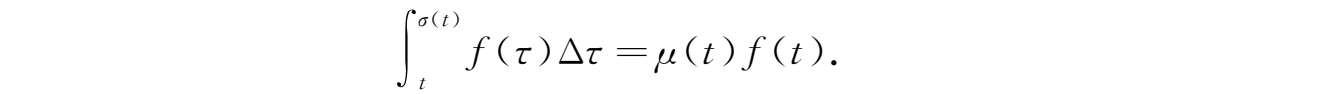
引理2.4
若
a
,
b
,
c
∈
 ,
α
∈
,
α
∈
 和
f
,
g
∈
C
rd
(
和
f
,
g
∈
C
rd
(
 ),则有下列结论成立:
),则有下列结论成立:
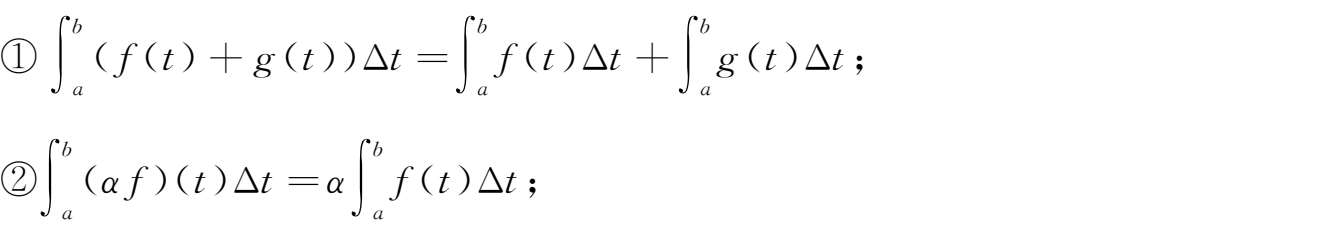
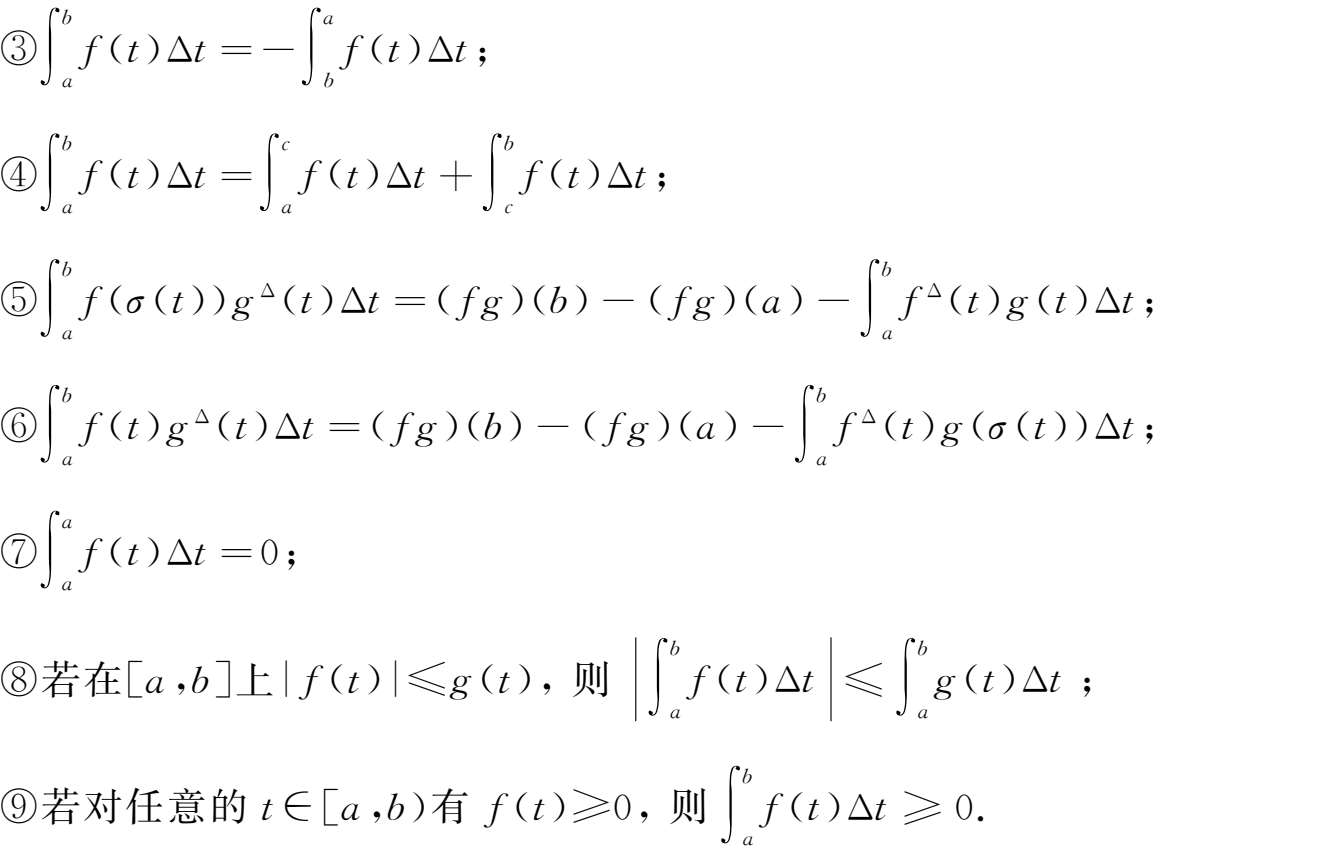
定义2.15
若函数
r
:
 →
→
 满足1+
μ
(
t
)
r
(
t
)≠0对所有
t
∈
满足1+
μ
(
t
)
r
(
t
)≠0对所有
t
∈
 k
成立,则称
r
为回归的。所有回归且右稠连续的函数
r
:
k
成立,则称
r
为回归的。所有回归且右稠连续的函数
r
:
 →
→
 的集合记为
的集合记为
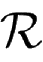 =
=
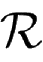 (
(
 )=
)=
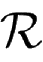 (
(
 ,
,
 ),定义正回归集合为
),定义正回归集合为
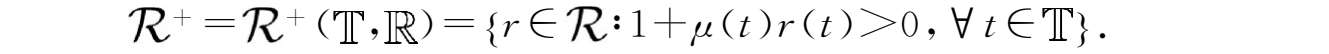
定义2.16
设
p
,
q
∈
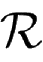 ,若对任意
t
∈
,若对任意
t
∈
 k
,则
k
,则

引理2.5
设
f
,
g
∈
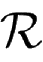 ,则
,则
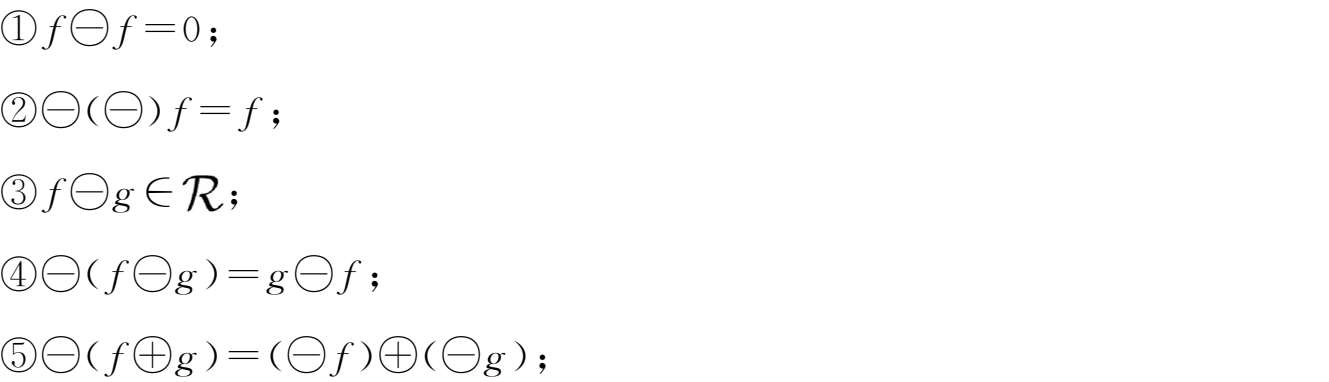

定义2.17 若 r 是回归函数,如果 e r 满足如下表达式
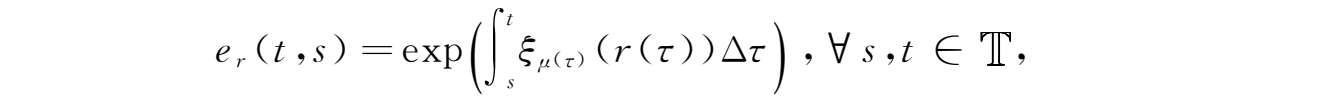
其中
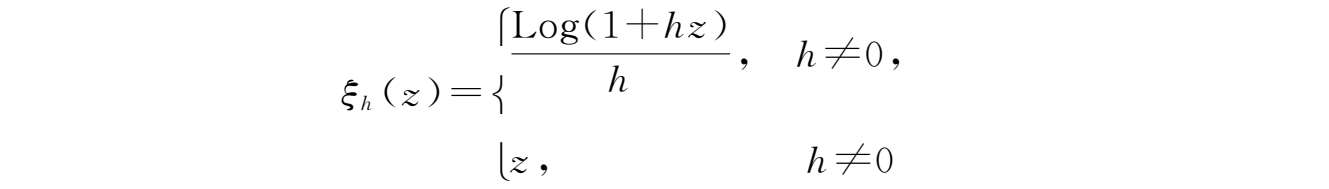
为柱变换,则称 e r 为广义指数函数。
引理2.6
设
f
∈
 和
t
0
∈
和
t
0
∈
 ,则
,则
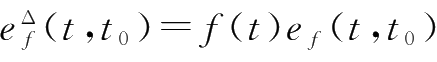 。
。
引理2.7
若
p
,
q
:
 →
→
 是回归函数,则
是回归函数,则
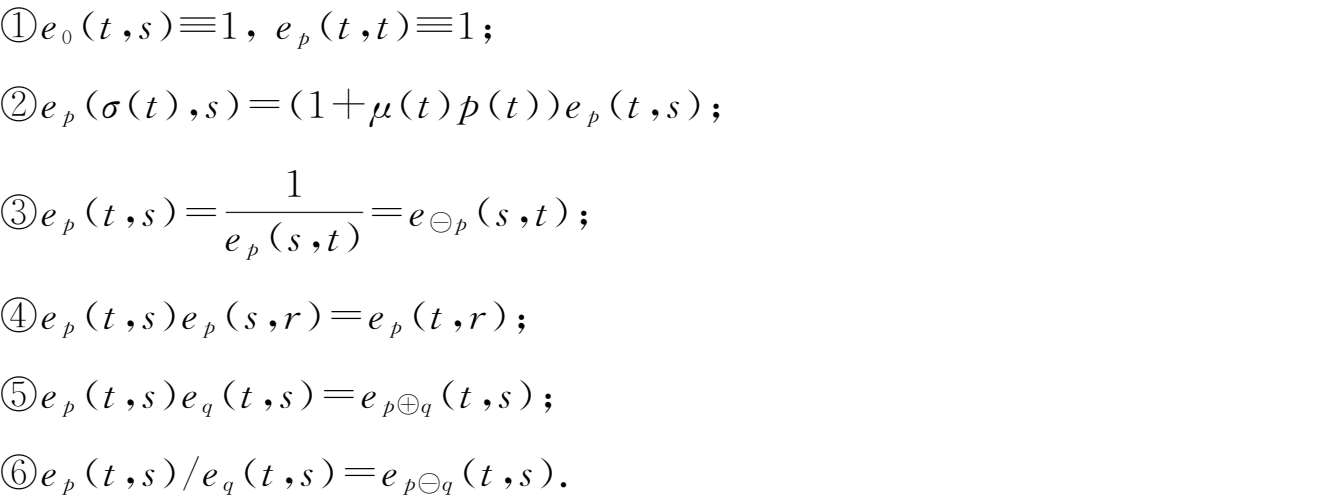
证明 ①由柱变换定义,可得
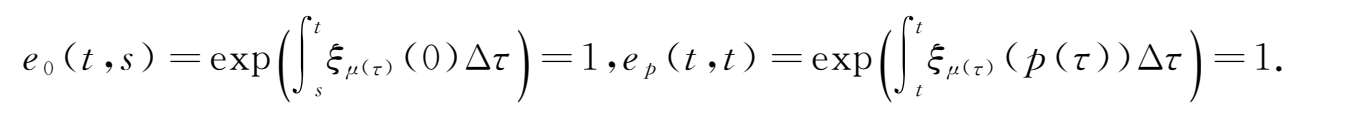
②根据引理2.4,有
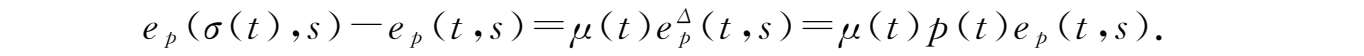
③由柱变换定义,可得
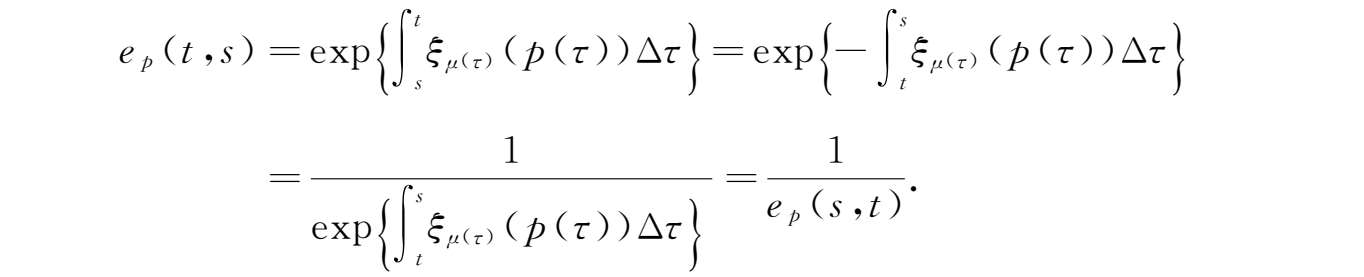
另一方面,
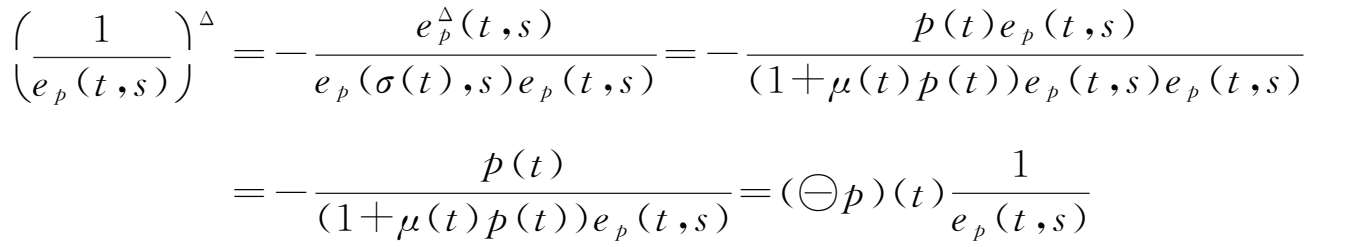
因此,
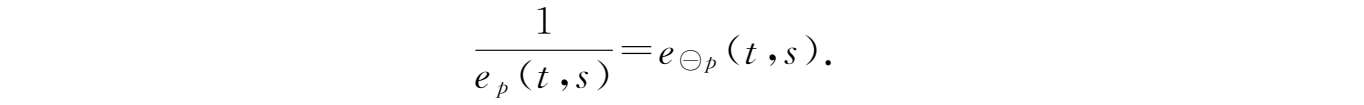
④由柱变换定义,可得
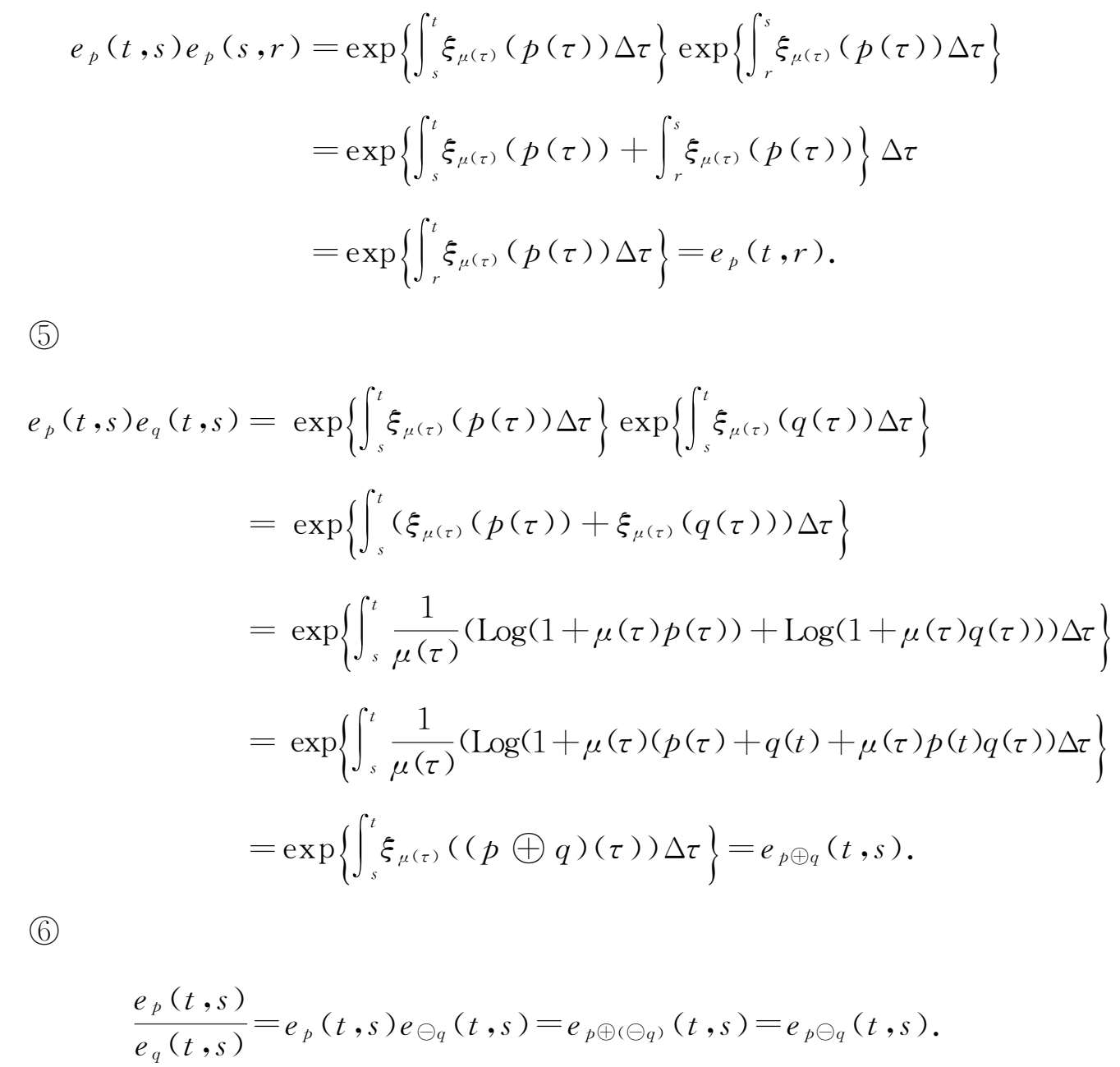
引理2.8 若 p ( t )≥0,则 e p ( t , s )>1,其中∀ t ≥ s .
引理2.9
若
p
∈
 +
,则有
+
,则有
①
e
p
(
t
,
s
)>0,∀
t
,
s
∈
 ;
;
②∀
t
,
s
∈
 ,若
p
(
t
)≤
q
(
t
),则
e
p
(
t
,
s
)≤
e
q
(
t
,
s
),∀
t
≥
s
.
,若
p
(
t
)≤
q
(
t
),则
e
p
(
t
,
s
)≤
e
q
(
t
,
s
),∀
t
≥
s
.
引理2.10
令
p
∈
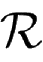 +
,若任意
a
,
b
,
c
∈
+
,若任意
a
,
b
,
c
∈
 ,则有[
e
p
(
c
,·)]
Δ
=-p
(
t
)[
e
p
(
c
,·)]
σ
,
,则有[
e
p
(
c
,·)]
Δ
=-p
(
t
)[
e
p
(
c
,·)]
σ
,
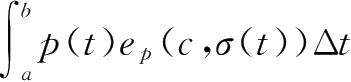 =e
p
(
c
,
a
)
-e
p
(
c
,
b
)
=e
p
(
c
,
a
)
-e
p
(
c
,
b
)
引理2.11
令
t
0
∈
 ,若在
,若在
 k
上
a
∈
k
上
a
∈
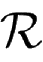 +
,则
e
a
(
t
,
t
0
)>0对所有
t
∈
+
,则
e
a
(
t
,
t
0
)>0对所有
t
∈
 都成立。
都成立。
引理2.12
令
t
0
∈
 ,若在
,若在
 k
上
a
∈
k
上
a
∈
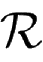 +
,则
e
a
(
t
,
t
0
)>0对所有
t
∈
+
,则
e
a
(
t
,
t
0
)>0对所有
t
∈
 都成立。
都成立。
引理2.13
(常数变异公式)设
p
∈
 ,
f
∈
C
rd
,对任意的
t
0
∈
,
f
∈
C
rd
,对任意的
t
0
∈
 ,
x
0
∈
,
x
0
∈
 。初值问题
。初值问题
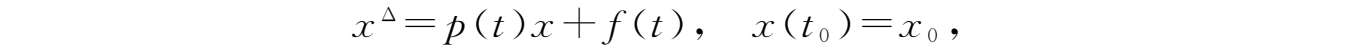
的唯一解可表示为
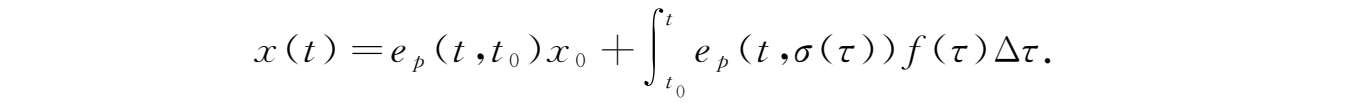
引理2.14
设
f
(
t
)是一个右稠密连续函数,而
c
(
t
)是一个正的右稠密连续函数且满足-
c
(
t
)∈
 +
。令
+
。令
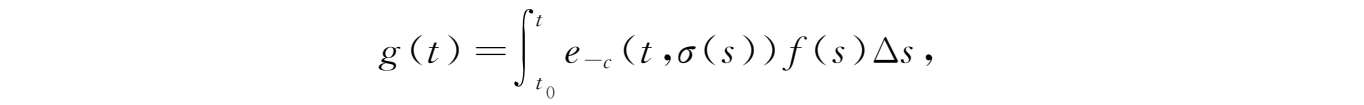
其中
t
0
∈
 ,则
,则
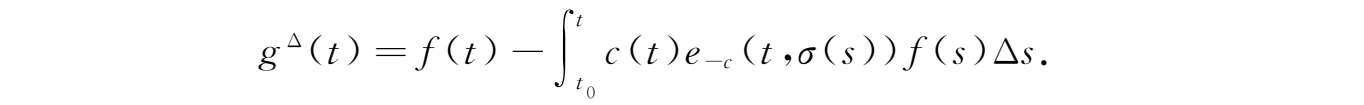
定义2.18
设
 为时标,定义后跃粗细度函数
ν
:
为时标,定义后跃粗细度函数
ν
:
 k
→[0,¥)如下:
k
→[0,¥)如下:
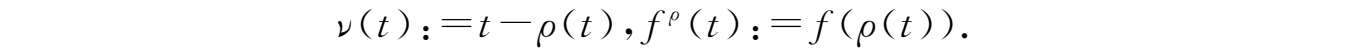
若
 有一个右离散的最小值
m
,则
有一个右离散的最小值
m
,则
 k
=
k
=
 -{
m
},否则
-{
m
},否则
 k
=
k
=
 。
。
定义2.19
设函数
f
:
 →
→
 且
t
∈
且
t
∈
 k
.定义
f
▽
(
t
)(若存在)为满足以下条件的数:对任意
ε
>0,存在
t
的邻域
U
(即对
δ
>0,
U
=(
t
-
δ
,
t
+
δ
)∩
k
.定义
f
▽
(
t
)(若存在)为满足以下条件的数:对任意
ε
>0,存在
t
的邻域
U
(即对
δ
>0,
U
=(
t
-
δ
,
t
+
δ
)∩
 ),使得
),使得
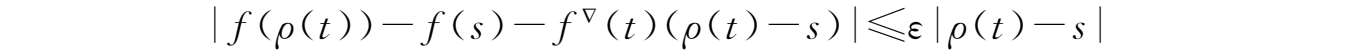
对所有 s ∈ U 成立,称 f ▽ ( t )为 f 在 t 处的Nabla导数。
引理2.15
若
f
:
 →
→
 且
t
∈
且
t
∈
 k
.则有:
k
.则有:
①若 f 在 t 点Nabla可微,则 f 在 t 点连续。
②若 f 在 t 点连续且 t 是左离散的,则 f 在 t 点Nabla可微,且
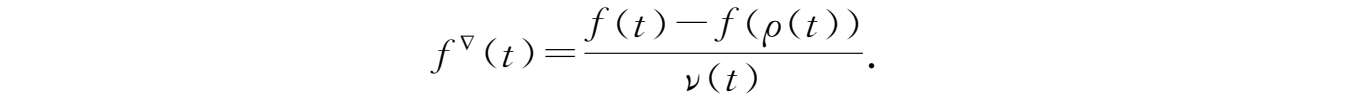
③若
t
是左稠密的,则
f
在
t
点Nabla可微当且仅当极限
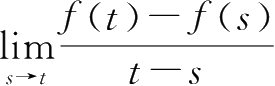 存在。即
存在。即
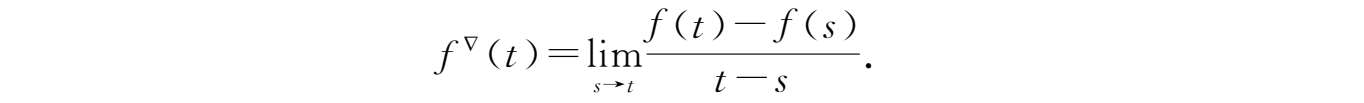
④若 f 在 t 点Nabla可微,则 f ( ρ ( t ))= f ( t )- ν ( t ) f ▽ ( t )。
引理2.16
若
f
,
g
:
 →
→
 在
t
∈
在
t
∈
 k
处Nabla可微。则:
k
处Nabla可微。则:
①和
f
+
g
:
 →
→
 在
t
点Nabla可微且
在
t
点Nabla可微且
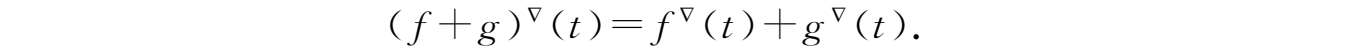
②对任意常数
α
,
αf
:
 →
→
 在
t
点Nabla可微且
在
t
点Nabla可微且
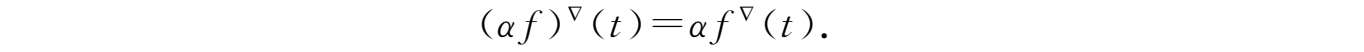
③积
f
,
g
:
 →
→
 在
t
点Nabla可微且
在
t
点Nabla可微且
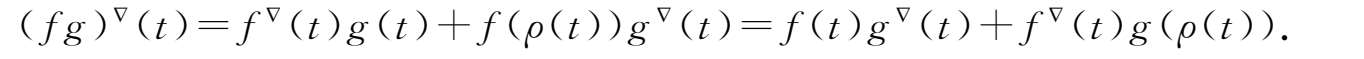
④若
f
(
t
)
f
(
ρ
(
t
))≠0,则
 在
t
点Nabla可微且
在
t
点Nabla可微且
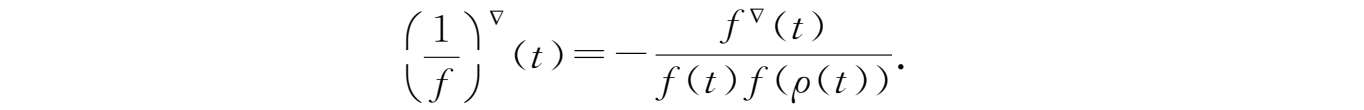
⑤若
g
(
t
)
g
(
ρ
(
t
))≠0,则
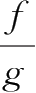 在
t
点Nabla可微且
在
t
点Nabla可微且
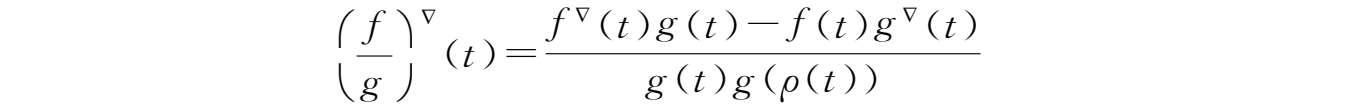
定义2.20
若函数
f
:
 →
→
 在
在
 中的左稠点处连续且在右稠点的右极限存在,则称其为左稠连续的。所有左稠连续的函数
f
:
中的左稠点处连续且在右稠点的右极限存在,则称其为左稠连续的。所有左稠连续的函数
f
:
 →
→
 的集合记为
的集合记为
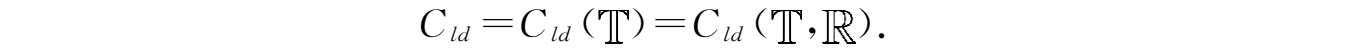
定义2.21
设函数
f
:
 →
→
 ,如果存在一个函数
F
:
,如果存在一个函数
F
:
 →
→
 ,使得对所有的
t
∈
,使得对所有的
t
∈
 k
,都有
F
▽
(
t
)=
f
(
t
),那么就称
F
(
t
)是
f
(
t
)的一个原函数。定义
f
(
t
)从
a
到
b
的Cauchy积分或定积分为
k
,都有
F
▽
(
t
)=
f
(
t
),那么就称
F
(
t
)是
f
(
t
)的一个原函数。定义
f
(
t
)从
a
到
b
的Cauchy积分或定积分为
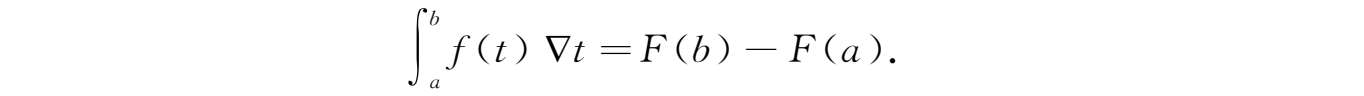
引理2.17
若
f
∈
C
ld
且
t
∈
 k
,则
k
,则
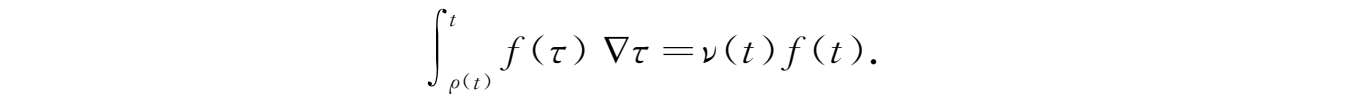
引理2.18
若
a
,
b
,
c
∈
 ,
α
∈
,
α
∈
 且
f
,
g
∈
C
ld
,则:
且
f
,
g
∈
C
ld
,则:
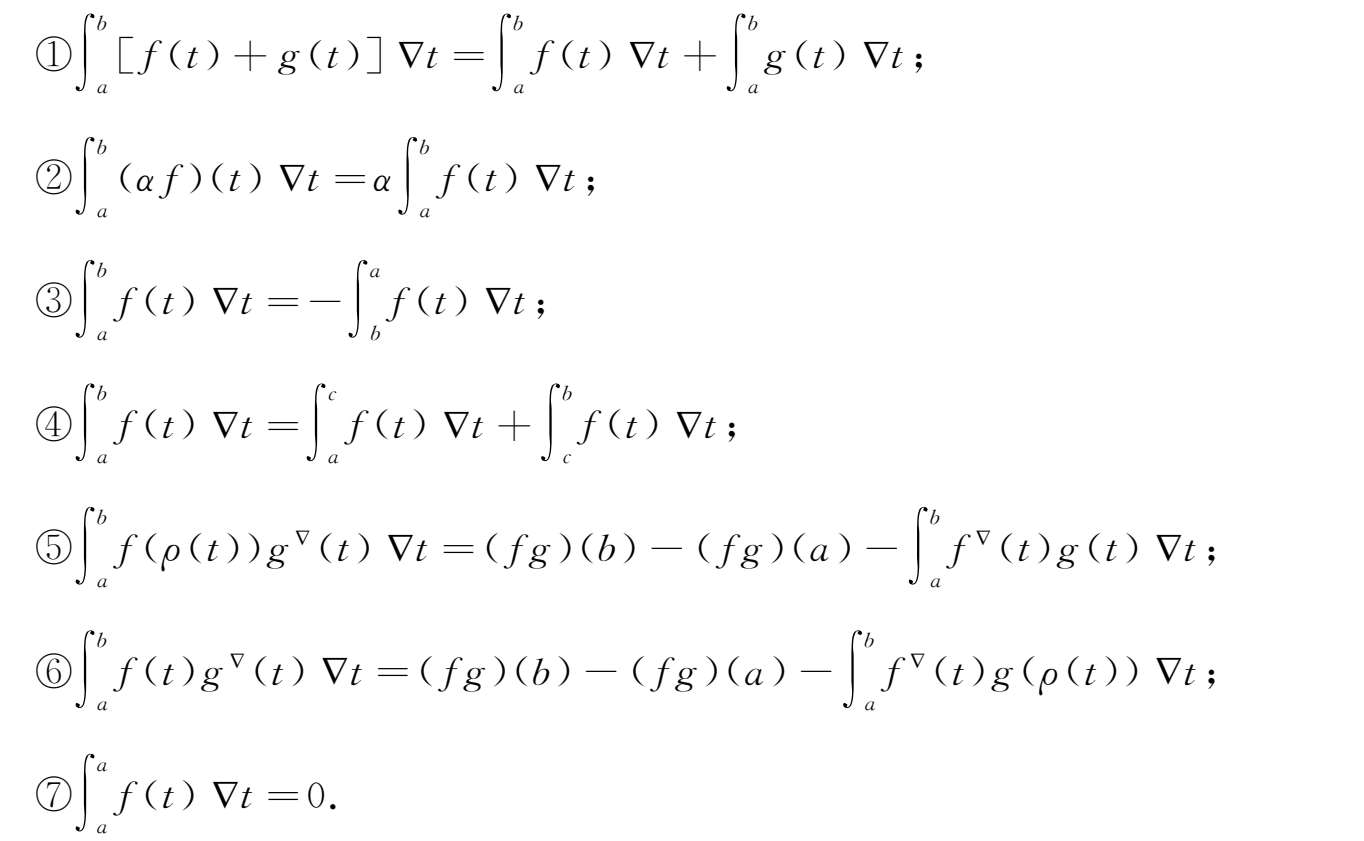
定义2.22
函数
p
:
 →
→
 称为
ν
-回归的,若1-
ν
(
t
)
p
(
t
)≠0对所有
t
∈
称为
ν
-回归的,若1-
ν
(
t
)
p
(
t
)≠0对所有
t
∈
 成立。所有
ν
-回归且左稠连续的函数
p
:
成立。所有
ν
-回归且左稠连续的函数
p
:
 →
→
 的集合记为
的集合记为
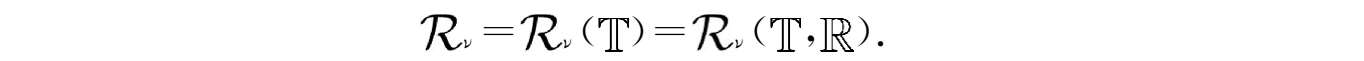
定义2.23
我们定义
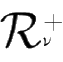 为正回归,
为正回归,
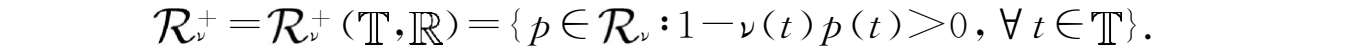
定义2.24
设
p
,
q
∈
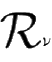 ,对所有
t
∈
,对所有
t
∈
 k
,我们定义“圈加”和“圈减”运算为
k
,我们定义“圈加”和“圈减”运算为
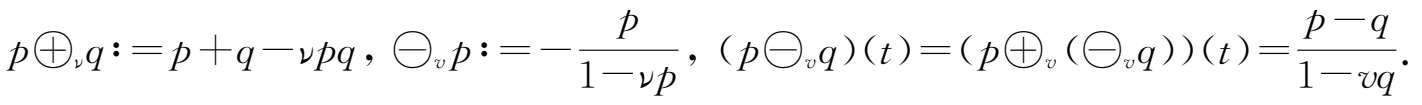
引理2.19
设
f
,
g
∈
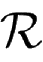 ν
,则
ν
,则
定义2.25
若
p
∈
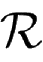 ν
,则我们定义Nabla指数函数为
ν
,则我们定义Nabla指数函数为
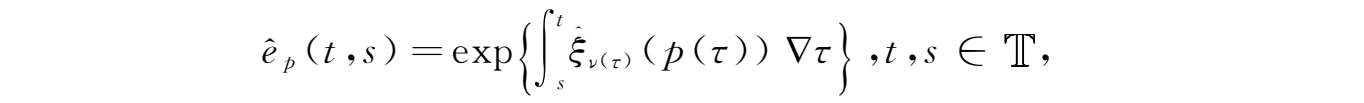
其中 ν -柱变换为
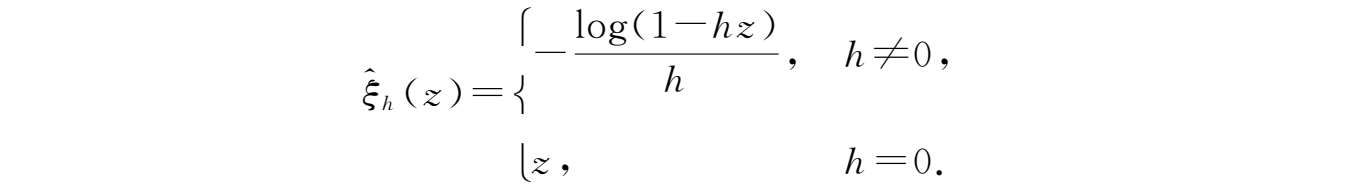
引理2.20
若
p
,
q
∈
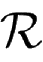 ν
,且
s
,
t
,
r
∈
ν
,且
s
,
t
,
r
∈
 ,则
,则

引理2.21
假设
p
∈
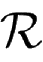 ν
且
t
0
∈
ν
且
t
0
∈
 ,若1-
ν
(
t
)
p
(
t
)>0对
t
∈
,若1-
ν
(
t
)
p
(
t
)>0对
t
∈
 k
成立,则
k
成立,则
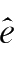 p
(
t
,
t
0
)>0对所有
t
∈
p
(
t
,
t
0
)>0对所有
t
∈
 都成立。
都成立。
引理2.22
设
f
(
t
)是一个左稠密连续函数,而
c
(
t
)是一个正的左稠密连续函数且满足
c
(
t
)∈
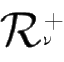 。令
。令
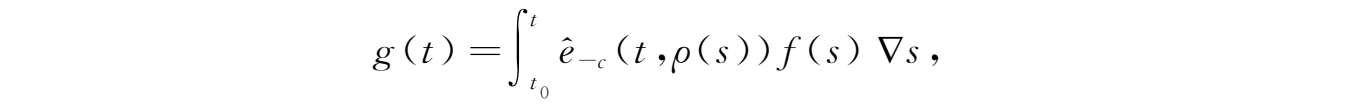
其中
t
0
∈
 ,则
,则
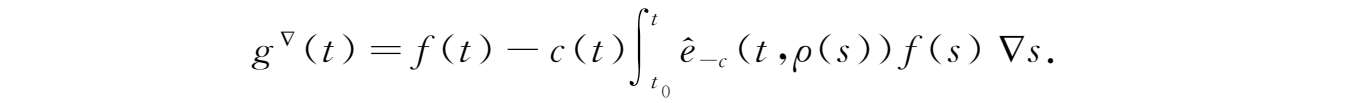
关于时标的更多知识,可参见文献[39,40]。