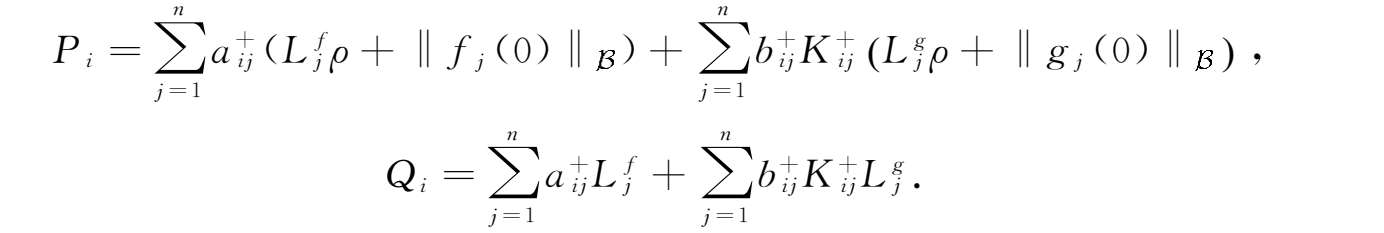对任意
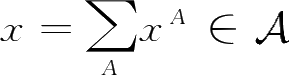 ,其范数定义为
,其范数定义为
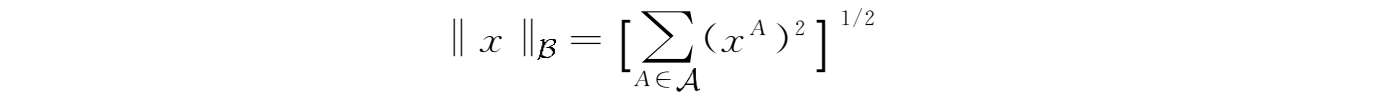
以及定义
x
=(
x
1
,
x
2
,…,
x
n
)
T
∈
 n
的范数为‖
x
‖
n
的范数为‖
x
‖
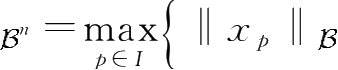 },其中
I
∶={1,2,…,
n
}。
},其中
I
∶={1,2,…,
n
}。
函数空间
PAP
0
(
 ,
,
 n
)定义为:
n
)定义为:
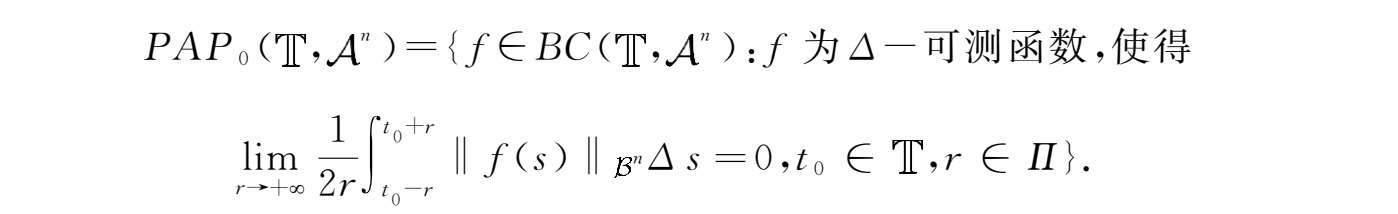
定义4.1
[82]
令
f
∈
BC
(
 ,
,
 n
),若
f
可以表示为
f
=
g
+
h
,其中
g
∈
AP
(
n
),若
f
可以表示为
f
=
g
+
h
,其中
g
∈
AP
(
 ,
,
 n
),
h
∈
PAP
0
(
n
),
h
∈
PAP
0
(
 ,
,
 n
)。则称
f
为伪概周期函数。
n
)。则称
f
为伪概周期函数。
记由所有此类函数所组成的集合为
PAP
(
 ,
,
 n
)。
n
)。
引理4.1
[82]
若
α
∈
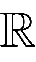 ,
f
,
g
∈
PAP
(
,
f
,
g
∈
PAP
(
 ,
,
 n
),则
αf
,
f
+
g
,
fg
∈
PAP
(
n
),则
αf
,
f
+
g
,
fg
∈
PAP
(
 ,
,
 n)。
n)。
引理4.2
[82]
若函数
f
∈
C
(
 ,
,
 n
)满足李普希茨条件,
x
∈
PAP
(
n
)满足李普希茨条件,
x
∈
PAP
(
 ,
,
 ),
τ
∈
C
),
τ
∈
C
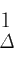 (
(
 ,
,
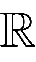 +
)∩
AP
(
+
)∩
AP
(
 ,
Π
)满足
,
Π
)满足
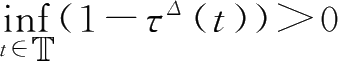 ,则
f
(
x
(·-
τ
(·)))∈
PAP
(
,则
f
(
x
(·-
τ
(·)))∈
PAP
(
 ,
,
 n
)。
n
)。
引理4.3
若函数
g
:
 →
→
 满足李普希茨条件,
K
:
满足李普希茨条件,
K
:
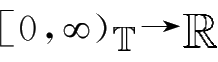 是连续右稠可积函数且
0
≤
是连续右稠可积函数且
0
≤
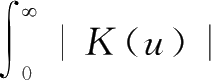 Δ
u
≤
K
+
(其中
K
+
是一个正常数),
φ
∈
PAP
(
Δ
u
≤
K
+
(其中
K
+
是一个正常数),
φ
∈
PAP
(
 ,
,
 ),则
Γ
:
t
→(
),则
Γ
:
t
→(
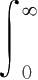 K
(
s
)
g
(
φ
(
t-s
))Δ
s
)属于
PAP
(
K
(
s
)
g
(
φ
(
t-s
))Δ
s
)属于
PAP
(
 ,
,
 )。
)。
证明
因为
φ
∈
PAP
(
 ,
,
 ),所以存在
φ
1
∈
AP
(
),所以存在
φ
1
∈
AP
(
 ,
,
 ),
φ
2
∈
PAP
0
(
),
φ
2
∈
PAP
0
(
 ,
,
 )使得
φ
=
φ
1
+
φ
2
.令
)使得
φ
=
φ
1
+
φ
2
.令
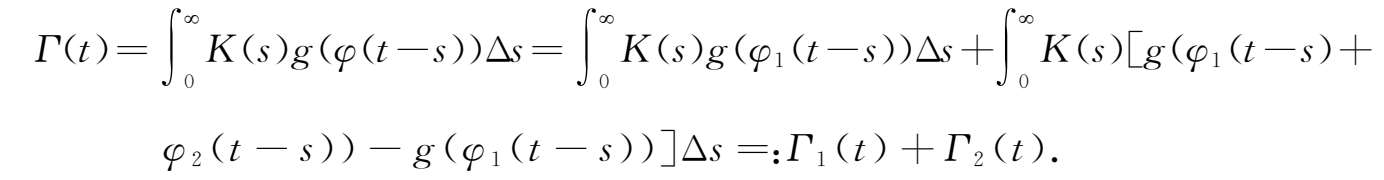
首先证明
Γ
1
∈
AP
(
 ,
,
 )。因为
g
满足李普希茨条件,所以存在一个正常数
L
,使得‖
g
(
u
1
)-
g
(
u
2
)‖
)。因为
g
满足李普希茨条件,所以存在一个正常数
L
,使得‖
g
(
u
1
)-
g
(
u
2
)‖
 对于所有的
u
1
,
u
2
∈
对于所有的
u
1
,
u
2
∈
 都成立。对于任给的
ε
>0,因为
φ
1
∈
AP
(
都成立。对于任给的
ε
>0,因为
φ
1
∈
AP
(
 ,
,
 ),所以可以找到一个实常数
l
=
l
(
ε
)>0,使得在每一个长度为
l
(
ε
)的区间内都至少存在一点
τ
=
τ
(
ε
)∈
Π
满足‖
φ
1
(
t
+
τ
)-
φ
1
(
t
)‖
),所以可以找到一个实常数
l
=
l
(
ε
)>0,使得在每一个长度为
l
(
ε
)的区间内都至少存在一点
τ
=
τ
(
ε
)∈
Π
满足‖
φ
1
(
t
+
τ
)-
φ
1
(
t
)‖
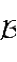 <
ε
对于∀
t
∈
<
ε
对于∀
t
∈
 ,然后
,然后
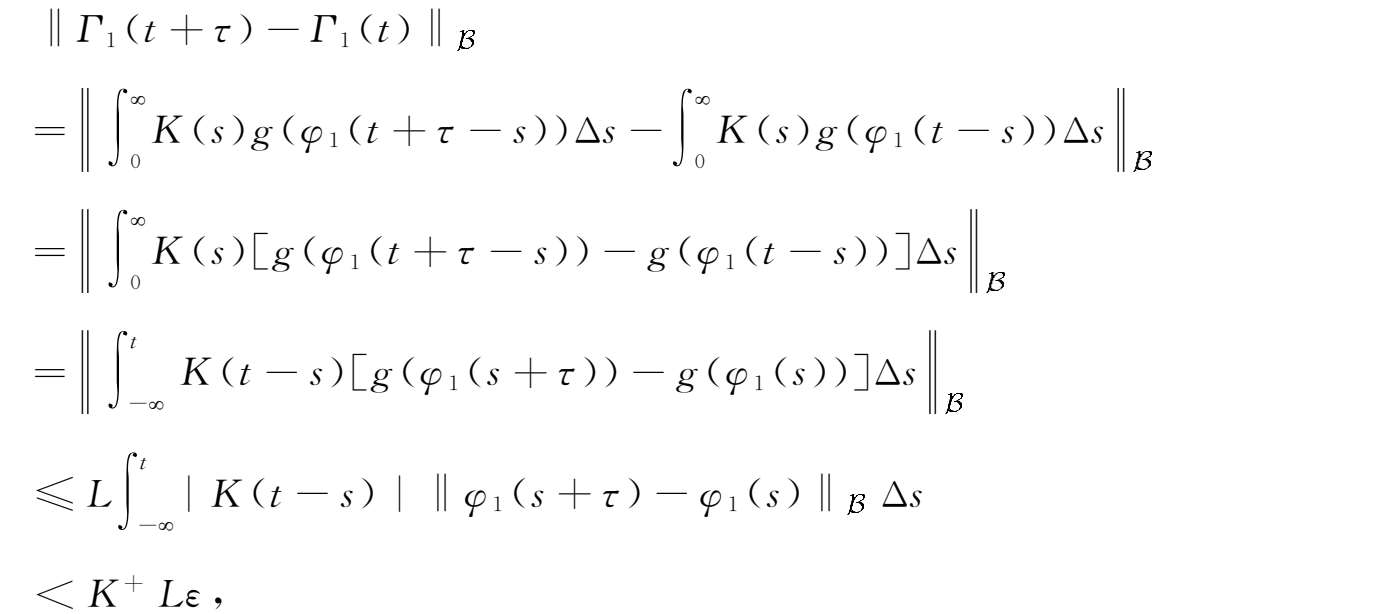
由此可得
Γ
1
∈
AP
(
 ,
,
 )。
)。
接下来证明
Γ
2
∈
PAP
0
(
 ,
,
 )。由
φ
2
∈
PAP
0
(
)。由
φ
2
∈
PAP
0
(
 ,
,
 )和勒贝格控制收敛定理,可得
)和勒贝格控制收敛定理,可得
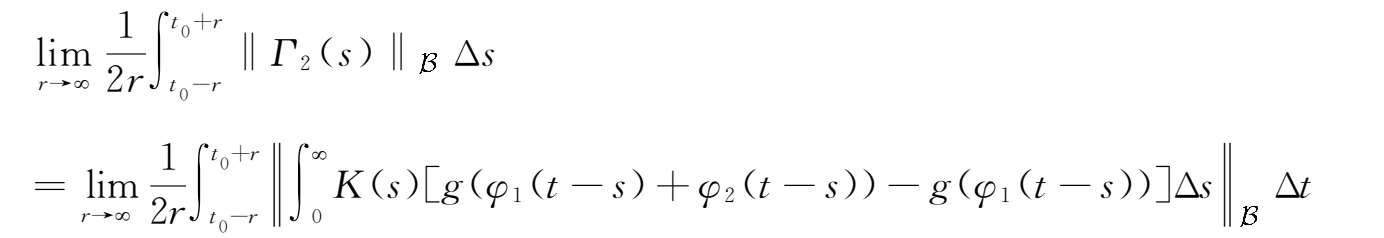
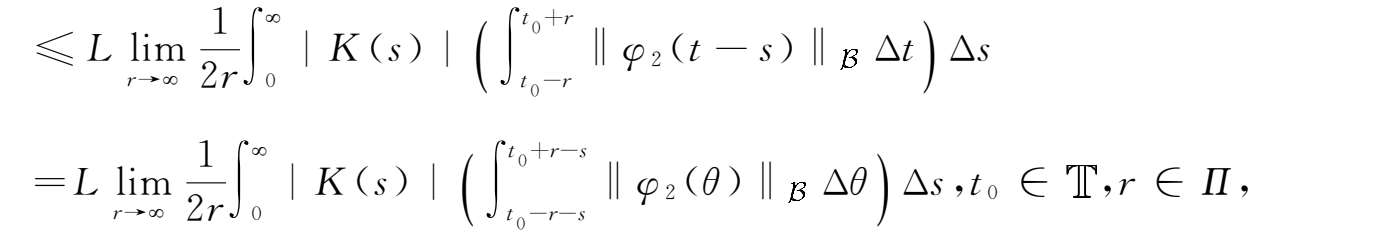
由此可得
Γ
2
∈
PAP
0
(
 ,
,
 )。因此,
Γ
∈
PAP
(
)。因此,
Γ
∈
PAP
(
 ,
,
 )。证毕。
)。证毕。
本章主要考虑了以下时标上具离散时滞和分布时滞的Clifford值细胞神经网络:
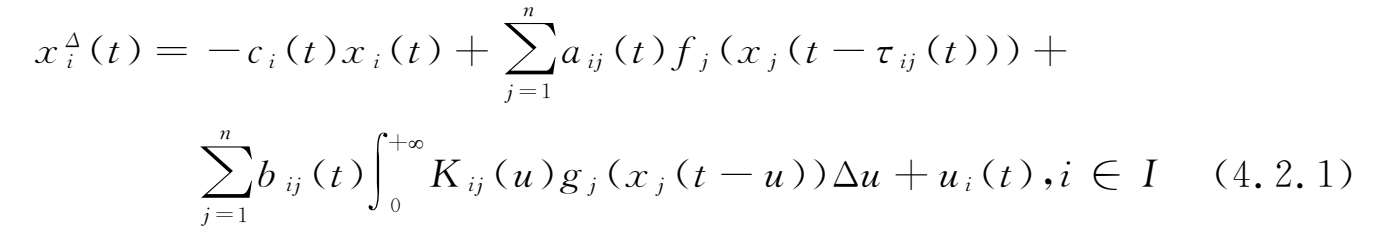
其中
 为概周期时标;
n
表示神经网络中神经元的条数;
x
i
(
t
)∈
为概周期时标;
n
表示神经网络中神经元的条数;
x
i
(
t
)∈
 表示第
i
条神经元在
t
时刻的状态变量;
c
i
(
t
)>0表示在时刻
t
,当断开神经网络与外部输入时,第
i
条神经元可能会出现重置而导致静止孤立状态的速率;
a
ij
(
t
)、
b
ij
(
t
)∈
表示第
i
条神经元在
t
时刻的状态变量;
c
i
(
t
)>0表示在时刻
t
,当断开神经网络与外部输入时,第
i
条神经元可能会出现重置而导致静止孤立状态的速率;
a
ij
(
t
)、
b
ij
(
t
)∈
 表示神经网络连接权重函数;
K
ij
(
t
)表示分布时滞核函数;
u
i
(
t
)∈
表示神经网络连接权重函数;
K
ij
(
t
)表示分布时滞核函数;
u
i
(
t
)∈
 表示在
t
时刻的第
i
条神经元外部输入;
f
j
,
g
j
:
表示在
t
时刻的第
i
条神经元外部输入;
f
j
,
g
j
:
 →
→
 表示信号传输过程中的作用函数。
表示信号传输过程中的作用函数。
为方便读者,现先引入以下记号:
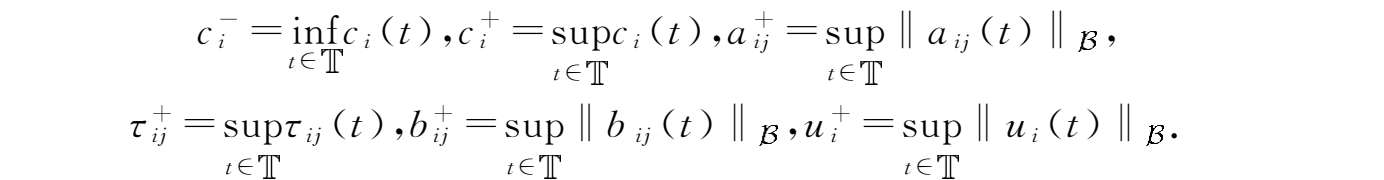
系统(4.2.1)具有以下形式的初始条件:
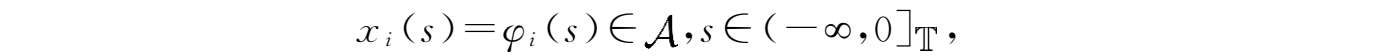
其中
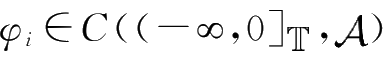 ,
i
∈
I
.
,
i
∈
I
.
注
4.1若
t
∈
 ,
u
∈
,
u
∈
 满足
t
-
u
∈
满足
t
-
u
∈
 ,则
,则
 =
=
 或
或
 =
=
 。
。
在本章中,先假设以下条件成立:
(
H
1
)
c
i
∈
AP
(
 ,
,
 +
)满足-
c
i
∈
+
)满足-
c
i
∈
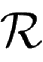 +
,
a
ij
,
b
ij
,
u
i
∈
PAP
(
+
,
a
ij
,
b
ij
,
u
i
∈
PAP
(
 ,
,
 ),
τ
ij
∈
C
),
τ
ij
∈
C
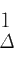 (
(
 ,
,
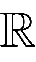 +
)∩
AP
(
+
)∩
AP
(
 ,
Π
)满足
,
Π
)满足
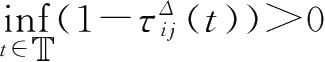 ,
i
,
j
∈
I
.
,
i
,
j
∈
I
.
(
H
2
)对于
i
,
j
∈
I
核函数
K
ij
:
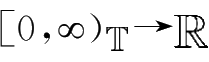 是连续右稠可积的,且满足0≤
是连续右稠可积的,且满足0≤
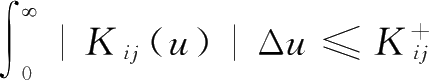 。
。
(
H
3
)存在正常数
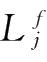 ,
,
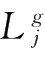 ,使得对一切的
u
,
v
∈
,使得对一切的
u
,
v
∈
 ,函数
f
j
,
g
j
∈
C
(
,函数
f
j
,
g
j
∈
C
(
 ,
,
 )满足
)满足
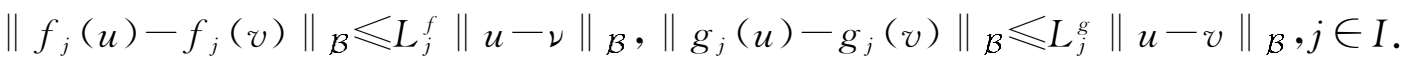
( H 4 )存在一个正常数 ρ ,使得
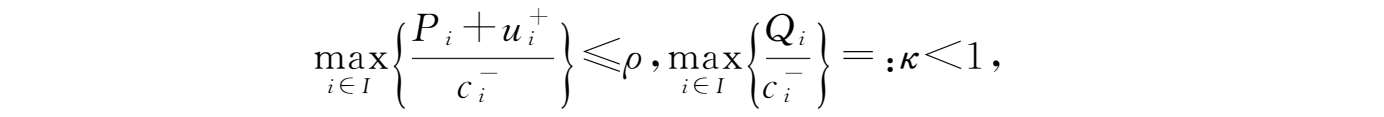
其中