




对任意
 定义其范数为
定义其范数为
 ;对任意
x
=(
x
1
,
x
2
,…,
x
n
)
T
∈
;对任意
x
=(
x
1
,
x
2
,…,
x
n
)
T
∈
 n
定义其范数为
n
定义其范数为
 ,其中
I
∶={1,2,…,
n
}。
,其中
I
∶={1,2,…,
n
}。
定义3.1
[88]
若对时标
 ,有下式成立
,有下式成立

则称时标
 为概周期时标。
为概周期时标。
在下文中,我们令
 为概周期时标。
为概周期时标。
注
3.1若
 是一个概周期时标,则对于
t
∈
是一个概周期时标,则对于
t
∈
 ,
τ
∈
Π
有
σ
(
t
+
τ
)=
σ
(
t
)+
τ
。
,
τ
∈
Π
有
σ
(
t
+
τ
)=
σ
(
t
)+
τ
。
定义3.2
[87]
令
 为概周期时标,
f
∈
C
(
为概周期时标,
f
∈
C
(
 ,
,
 )。若对任意
ε
>0,
f
的
ε
移位数集
)。若对任意
ε
>0,
f
的
ε
移位数集

是相对稠密的。即对任意给定 ε >0,存在常数 l ( ε )>0使得每个长度为 l ( ε )的区间内总有 τ ( ε )∈ E { ε , f }⊂ Π 满足

其中
τ
称为
f
的
ε
移位数,
l
(
ε
)称为
E
{
ε
,
f
}的包含长度。则称
f
是
 上的概周期函数。
上的概周期函数。
记由所有此类函数所组成的集合为
AP
(
 ,
,
 n
)。
n
)。
引理3.1
[87]
若
α
∈
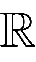 ,
f
,
g
∈
AP
(
,
f
,
g
∈
AP
(
 ,
,
 n
),则
αf
,
f
+
g
,
fg
∈
AP
(
n
),则
αf
,
f
+
g
,
fg
∈
AP
(
 ,
,
 n
)。
n
)。
引理3.2
[87]
若
x
∈
AP
(
 ,
,
 )且
τ
∈
AP
(
)且
τ
∈
AP
(
 ,
Π
),则
x
[·-
τ
(·)]∈
AP
(
,
Π
),则
x
[·-
τ
(·)]∈
AP
(
 ,
,
 )。
)。
引理3.3
[87]
若函数
f
∈
C
(
 ,
,
 n
)满足李普希茨条件,
ϕ
∈
AP
(
n
)满足李普希茨条件,
ϕ
∈
AP
(
 ,
,
 ),则
f
(
ϕ
(·))∈
AP
(
),则
f
(
ϕ
(·))∈
AP
(
 ,
,
 n
)。
n
)。
引理3.4
[84]
设
f
i
∈
AP
(
 ,
X
i
),其中
X
i
是一个Banach空间,
i
∈
I
.则对任给的
ε
>0,所有的函数
f
1
,
f
2
,…,
f
n
存在一个公共的
ε
-概周期集。
,
X
i
),其中
X
i
是一个Banach空间,
i
∈
I
.则对任给的
ε
>0,所有的函数
f
1
,
f
2
,…,
f
n
存在一个公共的
ε
-概周期集。
引理3.5
若
a
∈
AP
(
 ,
,
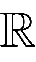 +
)满足-
a
∈
+
)满足-
a
∈
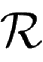 +
和
+
和
 ,
f
∈
AP
(
,
f
∈
AP
(
 ,
,
 ),则
),则

属于
AP
(
 ,
,
 )。
)。
证明
因为
a
∈
AP
(
 ,
,
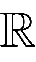 +
),
f
∈
AP
(
+
),
f
∈
AP
(
 ,
,
 ),所以根据引理3.4,对于任意的
ε
>0,存在一个
τ
∈
Π
使得
),所以根据引理3.4,对于任意的
ε
>0,存在一个
τ
∈
Π
使得

因此


即

根据引理2.9,用
e
-a(
σ
(
s
),
σ
(
t
))同时乘以等式(3.2.2)两边并在
 上积分,可得
上积分,可得

因此,由 σ ( s + τ )= σ ( s )+ τ ,有

然后,用 e - a ( t , σ ( s ))同时乘以等式(3.2.3)两边,可得


因此,可得

由不等式(3.2.1)和等式(3.2.5),易得

证毕。
本章,主要考虑了以下时标上具有时变时滞的Clifford值高阶Hopfield神经网络:

其中
 为概周期时标,
i
∈
I
;
n
表示神经网络中神经元的条数;
x
i
(
t
)∈
为概周期时标,
i
∈
I
;
n
表示神经网络中神经元的条数;
x
i
(
t
)∈
 表示第
i
条神经元在
t
时刻的状态变量;
a
i
(
t
)>0表示在
t
时刻,当断开神经网络和外部输入时,第
i
条神经元可能会出现重置而导致静止孤立状态的比例;
b
ij
(
t
)∈
表示第
i
条神经元在
t
时刻的状态变量;
a
i
(
t
)>0表示在
t
时刻,当断开神经网络和外部输入时,第
i
条神经元可能会出现重置而导致静止孤立状态的比例;
b
ij
(
t
)∈
 与
c
ijl
(
t
)∈
与
c
ijl
(
t
)∈
 分别表示神经网络的一阶与二阶连接权重函数;
τ
ij
(
t
),
δ
ijl
(
t
)和
v
ijl
(
t
)为
t
∈
分别表示神经网络的一阶与二阶连接权重函数;
τ
ij
(
t
),
δ
ijl
(
t
)和
v
ijl
(
t
)为
t
∈
 满足
t
-
τ
ij
(
t
),
t
-
δ
ijl
(
t
)和
t
-
v
ijl
(
t
)∈
满足
t
-
τ
ij
(
t
),
t
-
δ
ijl
(
t
)和
t
-
v
ijl
(
t
)∈
 的传输时滞;
I
i
(
t
)∈
的传输时滞;
I
i
(
t
)∈
 表示第
i
条神经元在
t
时刻的外部输入;
f
j
,
g
j
∶
表示第
i
条神经元在
t
时刻的外部输入;
f
j
,
g
j
∶
 →
→
 表示信号传输的激活函数。
表示信号传输的激活函数。
本章中,引入以下记号:

系统(3.2.6)具有以下形式的初始条件:

其中
 。
。
在本章中,假设以下条件成立:
(
S
1
)对于
i
,
j
,
l
∈
I
,
a
i
∈
AP
(
 ,
,
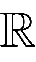 +
)满足-
a
i
∈
+
)满足-
a
i
∈
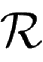 +
,
I
i
,
b
ij
,
c
ijl
∈
AP
(
+
,
I
i
,
b
ij
,
c
ijl
∈
AP
(
 ,
,
 )且
τ
ij
,
δ
ijl
,
ν
ijl
∈
C
(
)且
τ
ij
,
δ
ijl
,
ν
ijl
∈
C
(
 ,
,
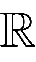 +
)∩
AP
(
+
)∩
AP
(
 ,
Π
)。
,
Π
)。
(
S
2
)存在正常数
 ,
,
 且对所有的
u
,
ν
∈
且对所有的
u
,
ν
∈
 ,函数
f
j
,
g
j
∈
C
(
,函数
f
j
,
g
j
∈
C
(
 ,
,
 )满足‖
f
j
(
u
)-
f
j
(
v
)‖
)满足‖
f
j
(
u
)-
f
j
(
v
)‖
 ‖
u
-
v
‖
u
-
v
 g
j
(
u
)-
g
j
(
v
)‖
g
j
(
u
)-
g
j
(
v
)‖
 ‖
u
-
v
‖
u
-
v
 且
f
j
(0)=
g
j
(0)=0,其中
j
∈
I
.
且
f
j
(0)=
g
j
(0)=0,其中
j
∈
I
.
( S 3 )存在一个正常数 r ,使得

其中
