




本章研究基坑地基内部的竖向自由位移场,是为下一章中分析基坑开挖对下卧已建地铁隧道的影响所展开的第一步必要的理论工作,因此,本节将重点分析坑底面下方既有隧道轴线位置处的土体竖向自由位移。首先假设隧道不存在的情况下,建立了如图 2.1 所示的分析模型:以基坑中心对应的地表面为原点建立三维笛卡尔坐标系,基坑横向(x轴向)开挖宽度B,纵向(y轴向)开挖长度L,竖向(z轴向)开挖深度H;下卧既有隧道轴线平行于y轴,轴线上任一点的坐标为( x
0
,y,z
0
)。基坑开挖后会形成 5 个卸载面(1 个坑底面+4 个侧壁面),其中坑底面编号为
 ,侧壁面编号分别为①、②、③和④。
,侧壁面编号分别为①、②、③和④。
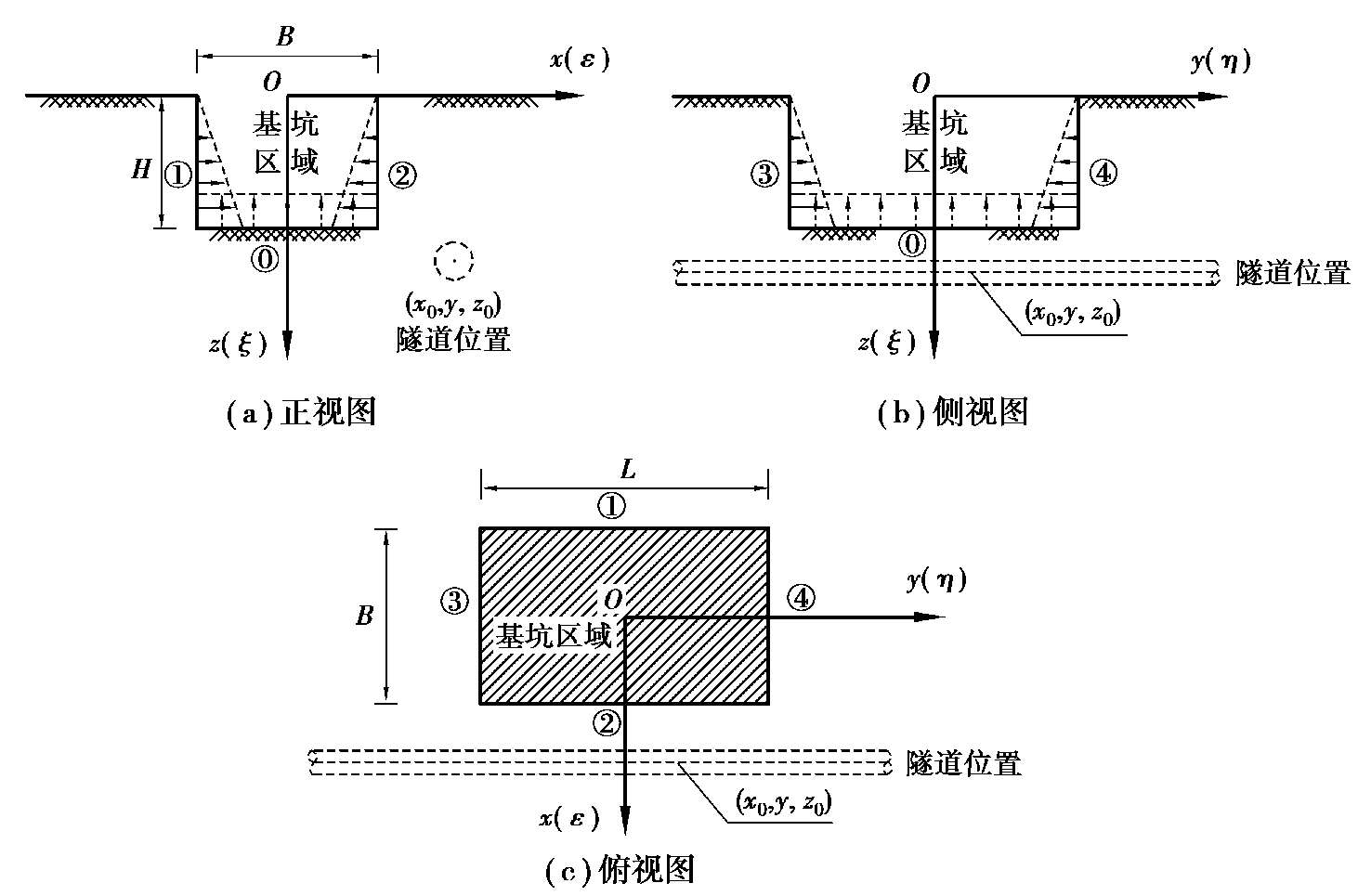
图 2.1 基坑开挖对邻近隧道影响的理论分析模型
目前,关于基坑开挖对周围土体及邻近隧道影响的理论成果基本都是建立在弹性均质半空间地基模型之上。实际上,天然地基在沉积过程中会造成竖直向力学性质的不同,而水平面内却往往是各向同性的,形成了以水平面为同性面的所谓横观各向同性地基。艾智勇等 [98,99] 提出了一种基于降阶法的三维分层地基状态空间解来分析荷载作用下弹性地基的附加应力和变形;张治国等 [100] 根据艾智勇的成果建立了一种多层地基中基坑开挖卸载对邻近隧道影响的连续弹性分析方法,改变了过去理论分析中只能在均质地基上求解此类工程问题的现状。但是上述方法均需要将各物理量在三维坐标系下进行Laplace积分变换,同时利用矩阵传递技术来实现各地层力场和位移场的应力求解,这种级数解法的推导和求解过程十分复杂,而且随着土体层数的增多容易发生计算溢出,其复杂而烦琐的计算不符合理论解简单、直接的使用要求,从而大大限制了该方法在实际工程中的推广运用。
为了简化计算,同时又能体现地基分层特性给土体变形性能带来的影响,本研究采用一种近似的简化弹性理论分析方法,其采用的弹性半空间层状地层分析模型如图 2.2 所示:假定基坑地基变形影响深度(H d )范围之内的土体是由n层有限厚度的弹性水平层构成,第i层土体底面的深度为h i ,并具有基本参数E i 、υ i 和γ i 。这里的地基变形影响深度H d ,是指该深度以下土层因开挖引起的附加变形可以忽略不计。关于H d 的下限值,本研究参照国家《建筑地基基础设计规范》(GB 50007—2011) [9] ,取开挖引起的地基竖向附加应力σ z ( y)不大于土体有效自重应力的 10%。
假设无隧道的情况下,基坑卸载引起的隧道位置处土体自由位移的计算如图 2.3 所示,隧道轴线位置上任一点的坐标为(x 0 ,y,z 0 ),则该点正下方所对应的第j层土体中任一点N的坐标为(x 0 ,y,z)。假设基坑施工在N点引起的土体三向附加应力分别为σ xj (z)、σ yj (z)和σ zj (z),根据胡克定律,N点处的竖向应变ε zj (z)为,
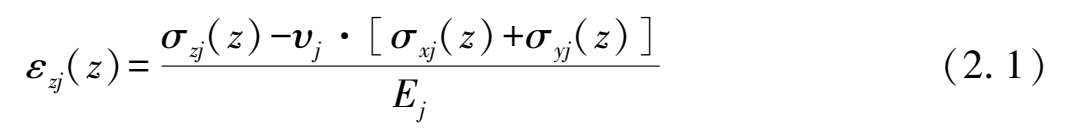
式中 E j ,υ j ——第j层土体的弹性模量和泊松比。
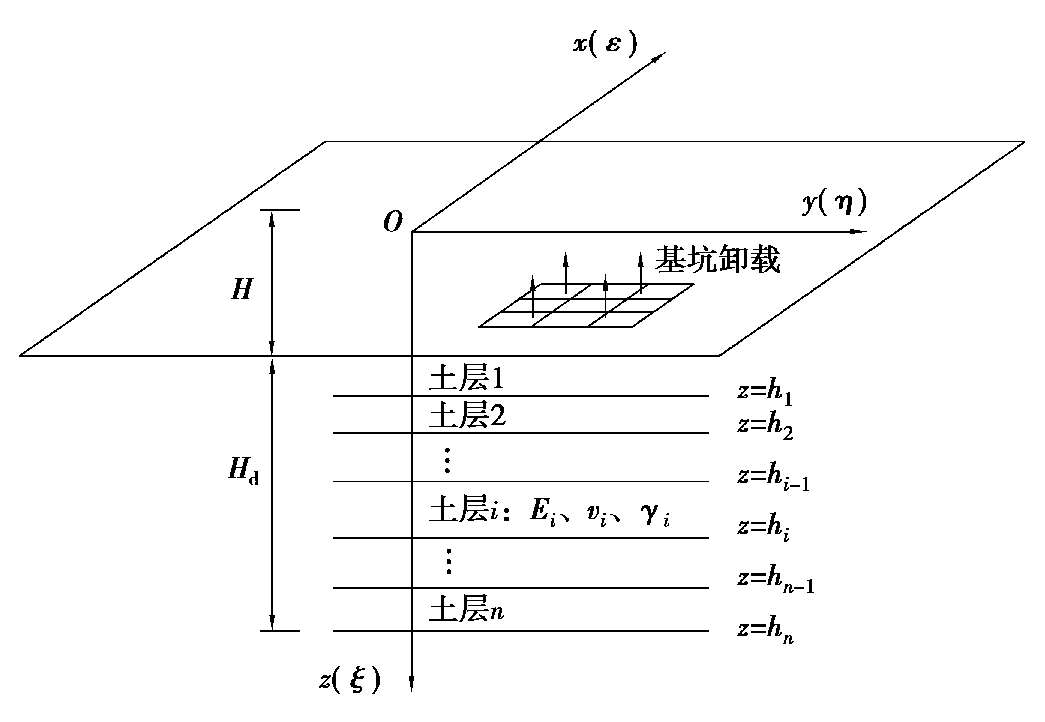
图 2.2 弹性半空间层状地基分析模型
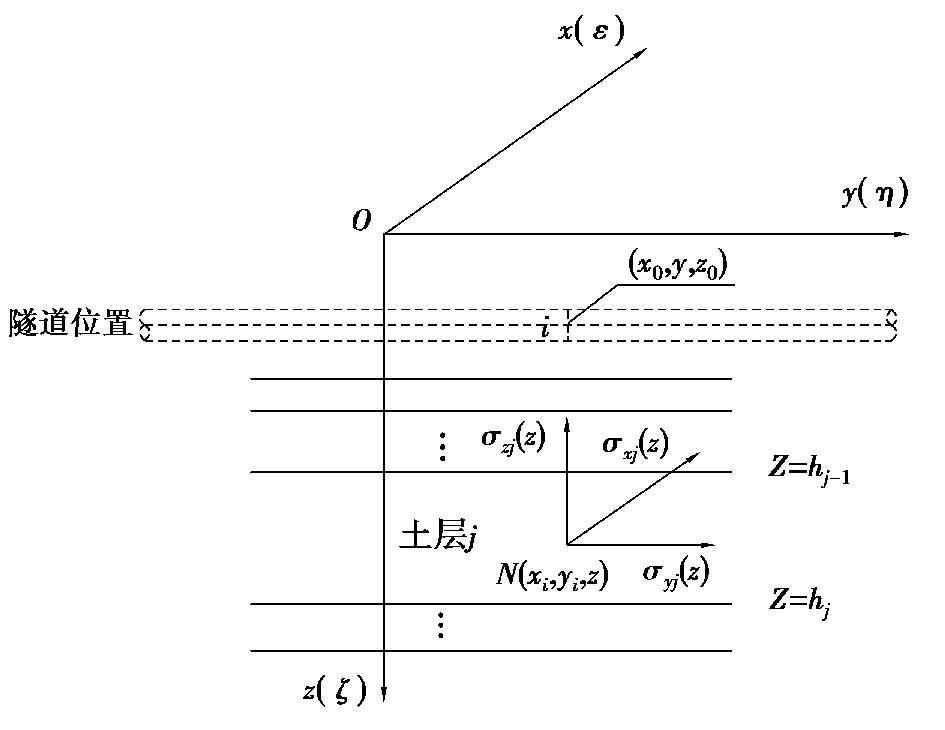
图 2.3 隧道轴线位置处土体竖向自由位移
采用积分的方法对第j层土体应变按地层厚度进行积分,即可得到该层土体的位移增量,再根据分层总和法的思路,将每一分层土体的位移增量进行叠加,即可得出隧道轴线位置任一点(x 0 ,y,z 0 )处的土体竖向自由位移w s (y)为,
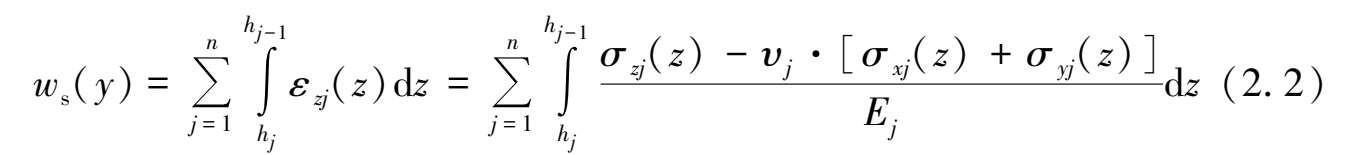
可见,只需要求解出基坑施工在下方地层j中任一点处引起的土体三向附加应力σ xj (z)、σ yj (z)和σ zj (z)之后,然后再代入式(2.2)中即可求解出基坑开挖在下卧隧道轴线位置上引起的土体自由场位移解w 1 (y)。