




在地下水丰富的城市,基坑施工容易受到地下水的影响,为防止发生渗透破坏,开挖前通常会采取一定的降水措施,将地下水位降低到坑底面以下一定位置。一方面,工程降水会使土骨架有效应力增大;另一方面,由于基坑内外存在的水头差会使土体产生渗流动水压力。这两种应力的作用都会使土体固结压密,并产生附加应力 [101] 。如果把土体开挖对邻近隧道的影响视为卸载行为,那么工程降水则相当于是一种加载行为。
根据Terzaghi有效应力理论可知,土的自重应力是土体有效自重引起的应力,地下水位下降使得土的有效自重应力增大。降水前后土体自重应力改变如图 2.5 所示,图中左侧阴影部分为降水引起的土体附加自重应力。由土体有效自重应力增大而引起的下方地层j中任一点处的土体竖向附加应力
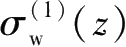 为,
为,

式中 h w1 ——降水前的地下水位;
h w2 ——降水后的地下水位;
γ w ——地下水重度,取 9.8 kN/ m 3 。
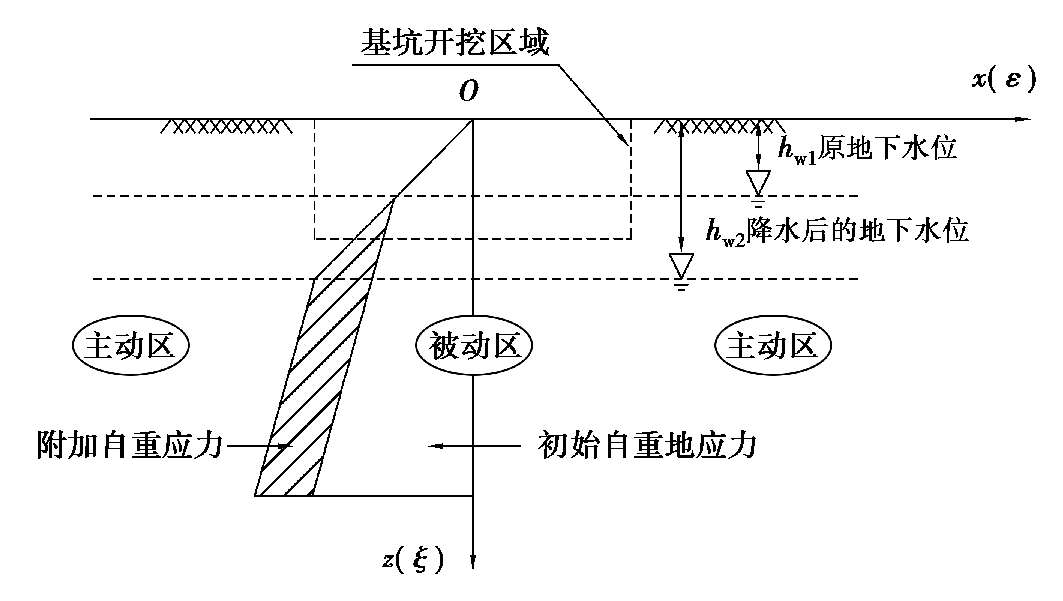
图 2.5 工程降水引起的土体附加应力
根据土体渗流理论可知,工程降水造成的基坑内外水头差会引起周围土体发生地下水流动,并给渗流区域内的土体颗粒施加动水压力,即渗透力,使得土体的附加应力发生变化(增大或减小)。在一维渗流场条件下,主动区的地下水渗流方向向下,引起土体有效应力增加;被动区的地下水渗流方向向上,引起土体有效应力减小。因此,由于地下水渗流而引起的下方地层j中任一点处的土体竖向附加应力
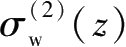 为,
为,

式中 i——水力坡降,i = (h 2 -h 1 )/ L w ,其中L w 为渗流路径长度。
当基坑由上而下分层开挖至第N s 时,基坑底面的土体竖向卸载效应相当于在开挖前的坑底面位置上施加一个大小为P 0 ,方向竖直向上的矩形分布荷载,P 0 大小为,

式中 γ i ,d i ——第i层开挖土体的有效重度和厚度。
由于城市地区实际地层的泊松比υ的变化范围并不大,一般为 0.25 ~ 0.4,则各土层变形量值大小主要取决于弹性模量E [102] 。黄栩 [31] 等通过分析开挖卸荷对邻近隧道的影响时也发现:地基弹性模量与厚度是较敏感的参数,而一定取值范围内泊松比的变化对计算结果影响却非常小以至可以忽略。考虑到半弹性空间中Mindlin应力基本解只包含了泊松比υ,与弹性模量E无关。因此,本研究采用均质半无限弹性体的Mindlin应力解来近似计算开挖卸载引起的下卧地层中任一点处产生的三向附加应力分量,应力计算中的泊松比近似取各地层泊松比的加权平均值υ。
整个坑底面卸载的影响相当于无数个单位面积上卸载影响的叠加之和,根据Mindlin应力解,采用积分的方法可得到编号为
 的坑底面土体竖向卸载在下方地层j中任一点处引起的附加应力分量
的坑底面土体竖向卸载在下方地层j中任一点处引起的附加应力分量
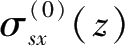 、
、
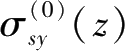 和
和
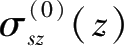 分别为,
分别为,
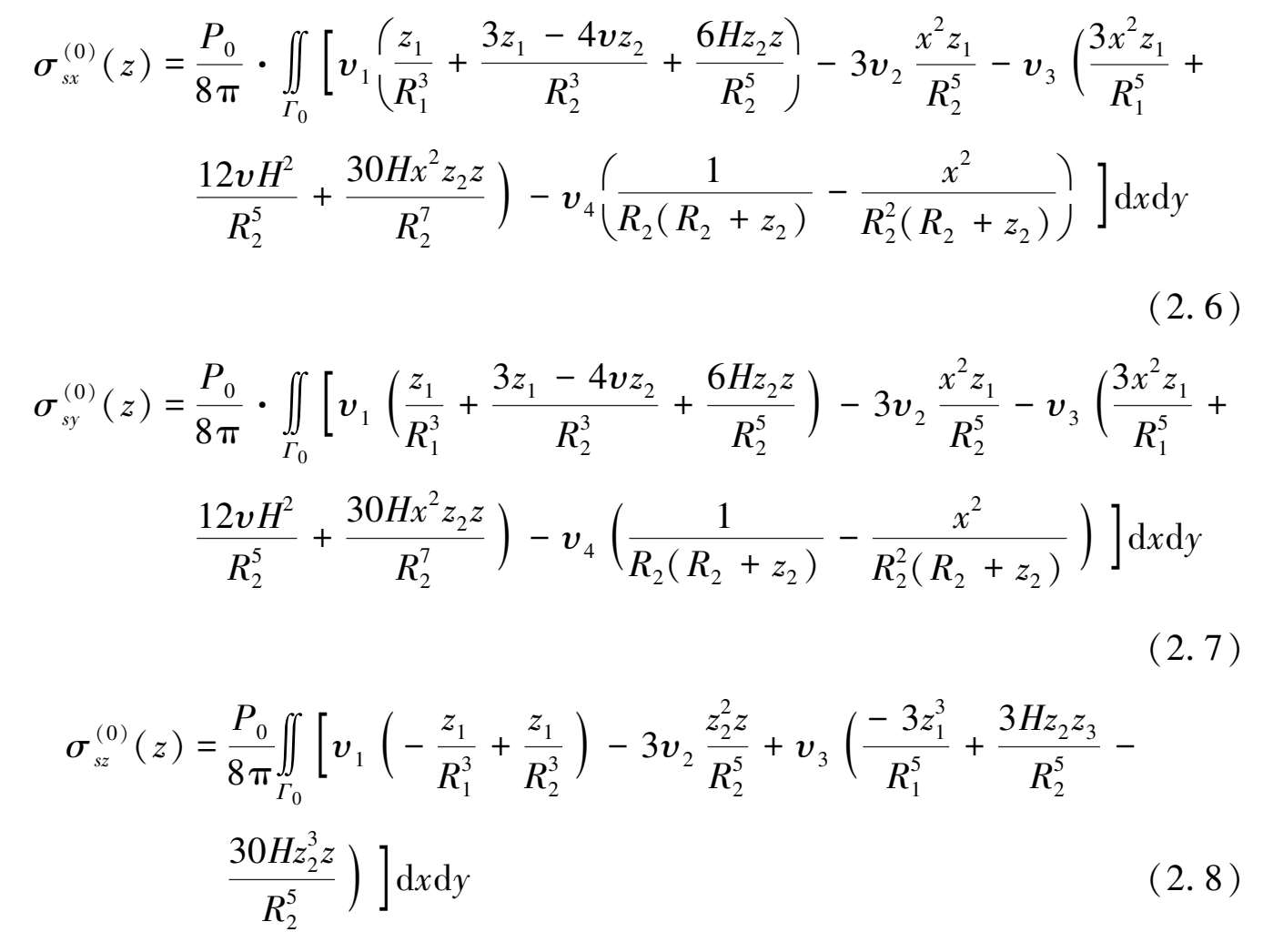
式(2.6)—式(2.8)中,泊松比相关常量υ
1
= (1-2
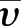 )/(1-
)/(1-
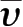 )、υ
2
= (3-4
)、υ
2
= (3-4
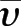 )/(1-
)/(1-
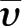 )、υ
3
= 1 /(1-
)、υ
3
= 1 /(1-
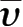 );积分区域Γ
0
为基坑底面对应的坐标范围,即:-B /2≤ε≤B /2,- L /2 ≤ η ≤ L /2,ξ = H;变量z
1
= z - H, z
2
= z+H, z
1
= 5z - H;变量R
1
=
);积分区域Γ
0
为基坑底面对应的坐标范围,即:-B /2≤ε≤B /2,- L /2 ≤ η ≤ L /2,ξ = H;变量z
1
= z - H, z
2
= z+H, z
1
= 5z - H;变量R
1
=
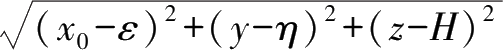 , R
2
=
, R
2
=
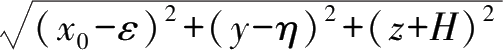 。
。
基坑开挖后,侧壁面内侧土体挖除消失,外侧主动区土体在围护墙体和支撑结构的约束下向内侧发生一定的水平位移,并产生水平卸载。因此,侧壁面上土体水平卸载作用的大小是主动区土体、围护墙体和支撑结构三者共同作用的结果。由弹性力学可知,该水平卸载效应同样会在下方地层中任一点处产生三向附加应力。本节以增量法理论 [103,104] 为基础来分析基坑侧壁面上土体水平卸载所引起的隧道竖向附加应力。
以基坑每向下分层开挖一次计为一个工况,图 2.6 是开始第 1 步开挖后的增量法计算原理示意图。图 2.6(a)为第 1 步开挖前作用于墙体的初始应力状态,此时墙体无位移,基坑四周侧壁面内、外侧均作用有静止土压力p 0 ,大小为,

式中 γ i ,z i ——本次工况开挖土层的平均重度和厚度;
K 0 ——静止土压力系数,取值可通过原位静止侧压力试验确定,在缺乏试验资料时也可通过以下经验公式估算:

式中
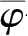 ——开挖土层有效内摩擦角的加权平均值;
——开挖土层有效内摩擦角的加权平均值;
OCR——土体超固结比。
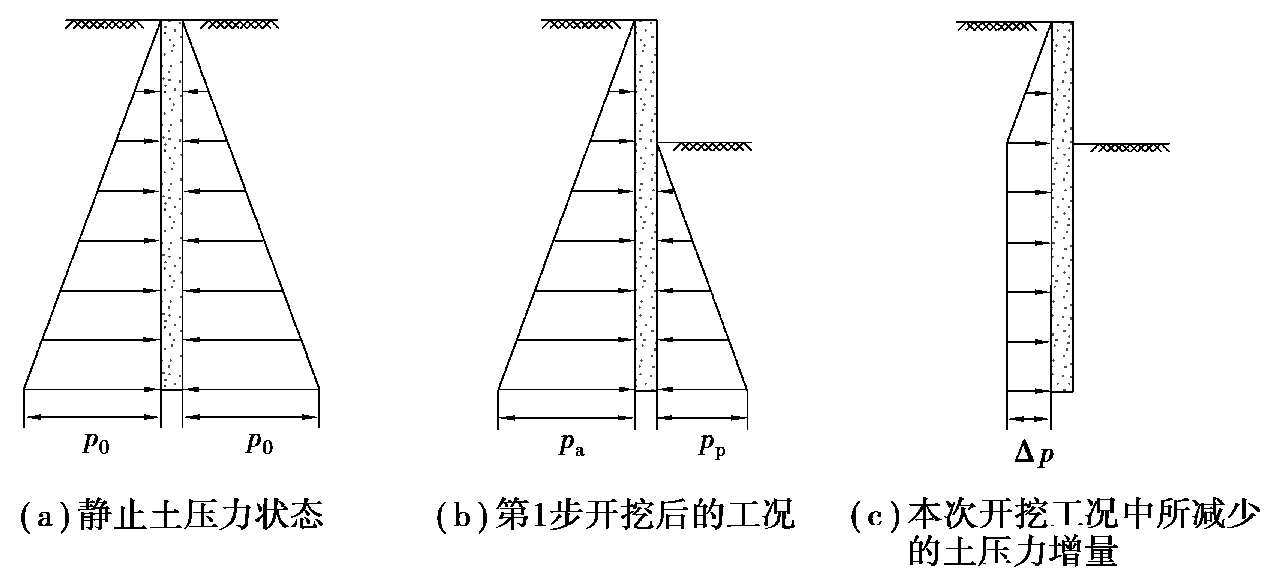
图 2.6 增量法计算原理
本次工况下作用在墙体上的土压力是上一工况开挖完成后到当前位置时的土压力增量,从另外一个角度上理解,该土压力增量正是基坑侧壁面开挖侧土体水平卸荷所产生的不平衡力,故可称为土体水平卸荷量。图 2.6(b)为第 1步开挖后的工况,假设此时墙体不动,侧壁面墙体内侧被动土压力为p p 、外侧主动土压力为p a ,其差值为Δp = p a -p p , 即为本次开挖工况中所减少的土压力增量,如图2.6(c)所示。但是,本次开挖工况所产生的荷载增量不仅仅限于土压力增量Δp,还包括挖去土体的土反力、围护墙压力和施加支撑预应力的荷载增量。
通过上述原理可知,增量法计算的关键是确定基坑在开挖过程中引起体系内力改变的每一个荷载增量 [104] ,由于传统的增量法假设墙体不动,没有考虑墙体增量位移对增量土压力的影响,而基坑土压力实测研究发现 [103] ,墙体位移与土压力密切相关。鉴于此,本研究采用迭代计算法来对增量土压力进行修正,假定墙体增量位移与增量荷载之间有如下线性迭代关系,
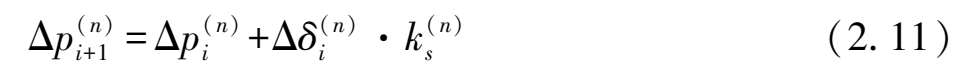
式中 上标n——第n次工况,以下编号同;
下标i——第i次迭代计算,以下编号同;
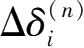 ——墙体上该点第i次迭代的增量位移;
——墙体上该点第i次迭代的增量位移;
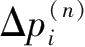 ——该点第i次迭代的增量荷载;
——该点第i次迭代的增量荷载;
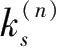 ——该点第n次工况的土弹簧刚度。
——该点第n次工况的土弹簧刚度。
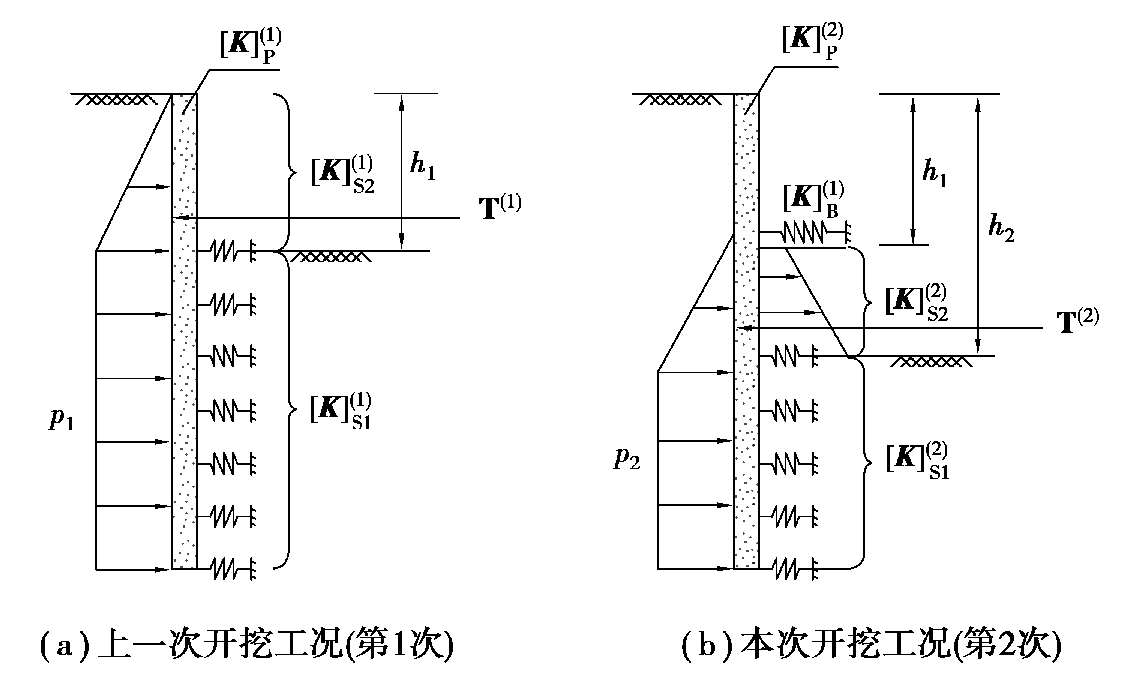
图 2.7 迭代增量法计算过程简图
图 2.7 给出了迭代增量法计算过程简图,每次开挖工况的增量荷载包含以下 3 部分:
①开挖侧土体的开挖卸载,即基坑侧壁面内侧被动区土压力减小所产生的土压力增量荷载,也可以认为是侧壁面外侧主动区土压力的增加所致。初始土压力增量荷载
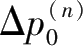 为
为
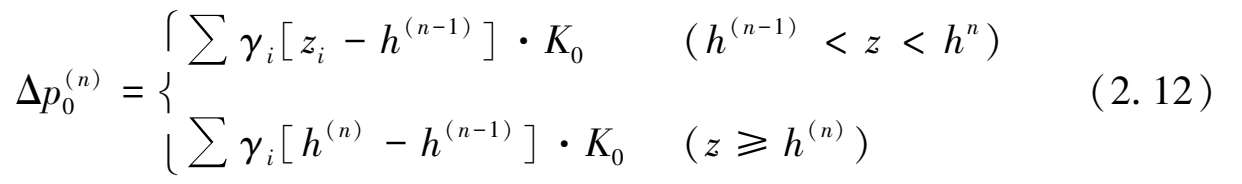
式中 h (n-1) ——上一工况的基坑开挖深度;
h
(n)
——本次工况的开挖深度;采用杆系有限单元法可以将初始土压力增量荷载
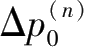 转换成等效节点荷载向量
转换成等效节点荷载向量
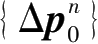 。
。
②开挖侧土弹簧消除所产生的增量荷载,本次工况开挖消除的土弹簧刚度矩阵为
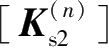 ,上一工况围护墙体位移向量为{Δδ
(n-1)
}。因此,本次工况开挖消除的土弹簧力所对应的增量荷载向量{f
(n)
}为
,上一工况围护墙体位移向量为{Δδ
(n-1)
}。因此,本次工况开挖消除的土弹簧力所对应的增量荷载向量{f
(n)
}为
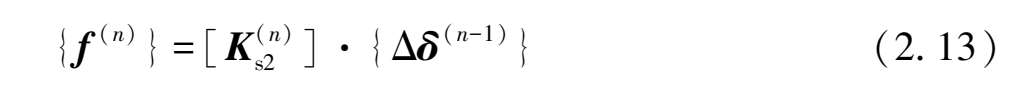
式 2.13 中,
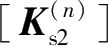 的下标s表示土弹簧,下标 2 表示开挖掉的土弹簧,下标若是1 则表示开挖后剩余的土弹簧,以下编号同。
的下标s表示土弹簧,下标 2 表示开挖掉的土弹簧,下标若是1 则表示开挖后剩余的土弹簧,以下编号同。
③本工况施加的支撑预应力所产生的增量荷载向量{T (n) }。对于预应力钢管支撑,{T (n) }取设计施加的预应力大小;对于混凝土支撑,由于无预应力,则取{T (n) }= 0。
将以上 3 部分增量荷载相加即得到本次开挖工况所产生的总初始增量荷载向量
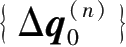 为
为
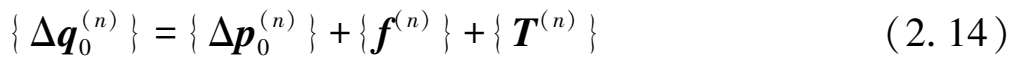
本次开挖工况所产生的总初始增量荷载向量
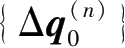 将由围护墙体、开挖侧剩余土弹簧、支撑结构这 3 部分体系来共同承担。因此,通过对围护墙体、开挖侧土体和支撑结构进行离散,梁单元尽量划分均匀,并且在地层变化面处、开挖面处和支撑设置处做节点处理,然后再分别求其刚度矩阵,如下:
将由围护墙体、开挖侧剩余土弹簧、支撑结构这 3 部分体系来共同承担。因此,通过对围护墙体、开挖侧土体和支撑结构进行离散,梁单元尽量划分均匀,并且在地层变化面处、开挖面处和支撑设置处做节点处理,然后再分别求其刚度矩阵,如下:
①计算围护墙体单元刚度矩阵
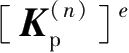 ,并由单元刚度矩阵转换成围护墙体整体刚度矩阵
,并由单元刚度矩阵转换成围护墙体整体刚度矩阵
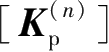 。此处,
。此处,
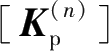 的下标p表示围护墙体,以下编号同。
的下标p表示围护墙体,以下编号同。
②计算本次工况开挖后,基坑侧壁面内侧剩余土弹簧的单元刚度矩阵
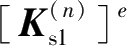 和由开挖消除的土弹簧单元刚度矩阵
和由开挖消除的土弹簧单元刚度矩阵
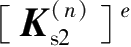 ,并分别将其转换成整体单元刚度矩阵
,并分别将其转换成整体单元刚度矩阵
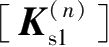 、
、
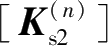 。
。
③考虑到本次工况施加的支撑并没有立即发挥作用,计算取上一次工况施加支撑的单元刚度矩阵
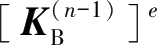 ,将其转换成整体刚度矩阵
,将其转换成整体刚度矩阵
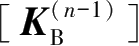 。此处,
。此处,
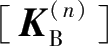 的下标B表示支撑结构,以下编号同。
的下标B表示支撑结构,以下编号同。
故本次开挖工况对应的结构总刚度矩阵为,
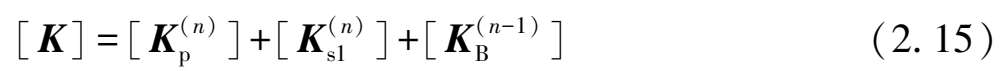
本次开挖工况所对应的初始有限元平衡方程为,
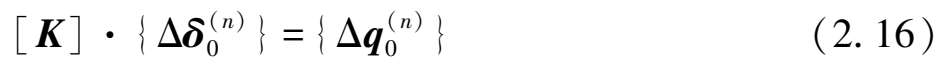
采用杆系有限单元法联合式(2.12)—式(2.16)即可计算出本次工况增量荷载引起的初始围护墙体增量位移
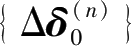 和增量土压力
和增量土压力
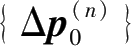 ,然后将
,然后将
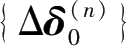 和
和
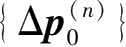 代入迭代关系式(2.11)中对增量土压力进行修正,再以修正后的荷载代入式(2.16)中进行计算,如此反复迭代,直至前后两次增量土压力
代入迭代关系式(2.11)中对增量土压力进行修正,再以修正后的荷载代入式(2.16)中进行计算,如此反复迭代,直至前后两次增量土压力
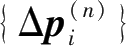 、
、
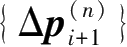 之间的差异可以忽略不计为止。此时,对应的
之间的差异可以忽略不计为止。此时,对应的
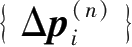 和
和
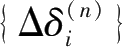 即为本次工况(第n次工况)下围护墙体最终增量土压力{Δp
(n)
}和最终增量位移{Δδ
(n)
}。
即为本次工况(第n次工况)下围护墙体最终增量土压力{Δp
(n)
}和最终增量位移{Δδ
(n)
}。
基坑四周侧壁面上的土体水平卸载量等于围护墙体的增量土压力,侧壁面上的土体水平位移等于围护墙体的水平位移。因此,当基坑开挖由上而下分层开挖至第N s 层时,分别将之前每次开挖工况迭代计算所得出围护墙体增量土压力{Δp (n) }和增量位移累{Δδ (n) }计求和,即可得基坑侧壁面土体总水平卸荷量向量{P s }和围护墙体总水平位移向量{w s },如下,
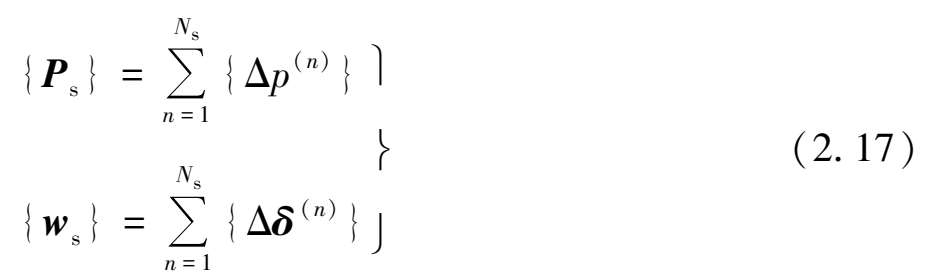
求出编号为①的基坑侧壁面上的土体总水平卸荷向量{P s }后,采用插值法拟合出其对应的连续函数P s 。整个侧壁面卸载的影响相当于无数个单位面积上卸载影响的叠加之和,根据Mindlin应力解,采用积分的方法可得到编号为①的基坑侧壁面上土体水平卸载在下方地层j中任一点处引起的附加应力分量
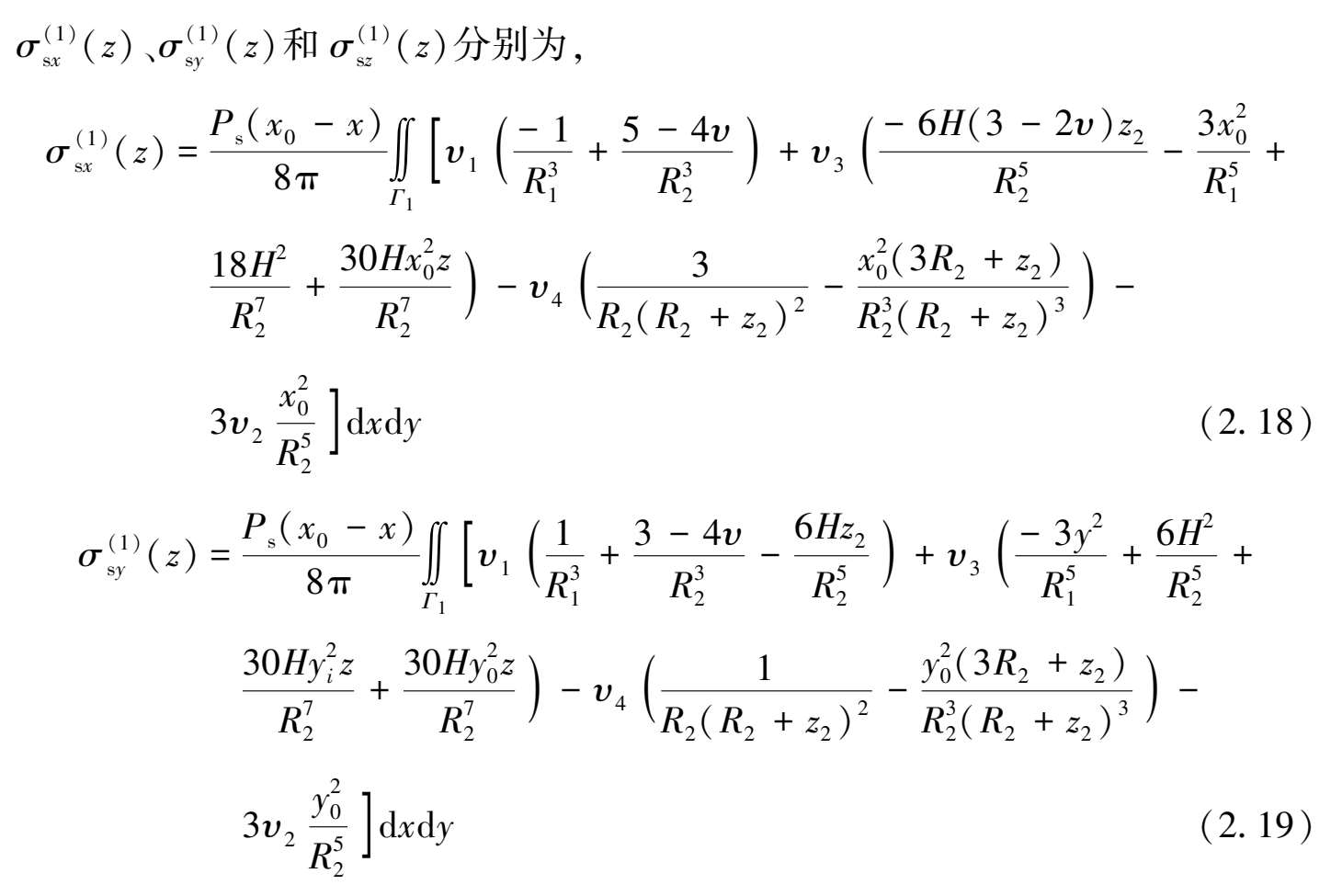
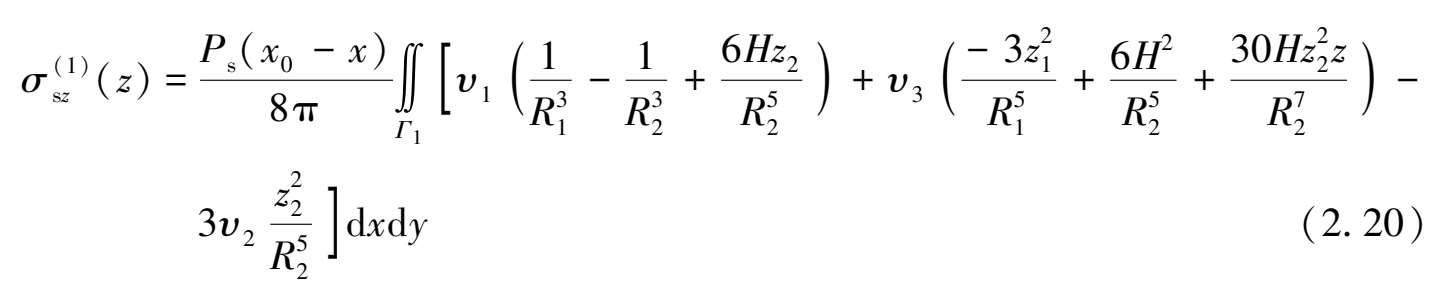
式(2.18)—式(2.20)中,积分区域Γ 1 为编号为①的基坑侧壁面对应的坐标范围,即:ε =B /2,-L /2≤η≤L /2,-H/ 2≤η≤H/ 2。
类似于
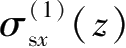 、
、
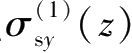 和
和
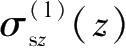 的推导,可以分别求出编号为②、③和④的基坑侧壁面上土体水平卸载在下方地层中任一点处引起的三向附加应力,即编号为②的侧壁面水平卸荷产生的
的推导,可以分别求出编号为②、③和④的基坑侧壁面上土体水平卸载在下方地层中任一点处引起的三向附加应力,即编号为②的侧壁面水平卸荷产生的
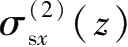 、
、
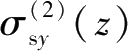 、
、
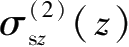 ;编号为③的侧壁面水平卸荷产生的
;编号为③的侧壁面水平卸荷产生的
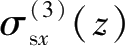 、
、
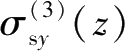 、
、
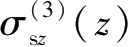 ;以及编号为④的侧壁面水平卸荷产生的
;以及编号为④的侧壁面水平卸荷产生的
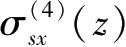 、
、
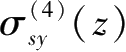 、
、
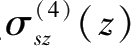 。具体过程及公式不再赘述。
。具体过程及公式不再赘述。
根据 2.3.3 小节中采用迭代增量法所计算出某个基坑侧壁面上围护墙体总水平位移向量{w s }之后,则可进一步得到该面围护墙对侧壁面土体的水平作用力为,

求出{P
p
}之后,采用差值法拟合出其对应的连续函数P
p
,类似于 2.3.2 节中
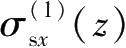 、
、
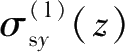 和
和
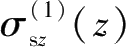 的推导,可以分别求解出 4 个侧壁面上围护墙的水平作用在下方地层j中任一点处引起的三向附加应力,分别为编号为①的侧壁面围护墙产生的
的推导,可以分别求解出 4 个侧壁面上围护墙的水平作用在下方地层j中任一点处引起的三向附加应力,分别为编号为①的侧壁面围护墙产生的
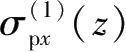 、
、
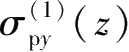 和
和
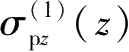 ;编号为②的侧壁面围护墙产生的
;编号为②的侧壁面围护墙产生的
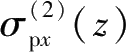 、
、
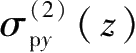 和
和
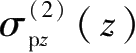 ;编号为③的侧壁面围护墙产生的
;编号为③的侧壁面围护墙产生的
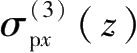 、
、
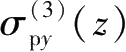 和
和
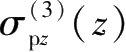 ;以及编号为④的侧壁面围护墙产生的
;以及编号为④的侧壁面围护墙产生的
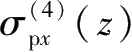 、
、
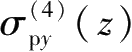 和
和
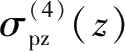 。具体过程及公式不再赘述。
。具体过程及公式不再赘述。
根据基坑侧壁面上围护墙体总水平位移向量{w s },可以得到该侧壁面上第i道支撑作用节点的位移分量δ i ,则可进一步得到该道支撑对侧壁面上土体的水平作用力为,

式中 (EI) B ——第i道支撑的轴向抗压刚度。
同理,将P
B
i
代入Mindlin应力解,即可得到第i层支撑结构的水平作用在下方地层下方j中处任一点处引起的附加应力分量
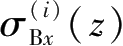 、
、
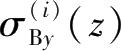 和
和
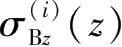 ,具体过程不再详述。
,具体过程不再详述。
当基坑分层开挖至第N s 层时,根据叠加原理,分别将工程降水、基坑底面土体竖向卸载、侧壁面土体水平卸载、围护墙体和支撑结构水平作用等因素所引起的下方地层j中任一点处引起的三向附加应力进行叠加,即可得到基坑施工在下方地层j中任一点处引起的三向总附加应力分别为,
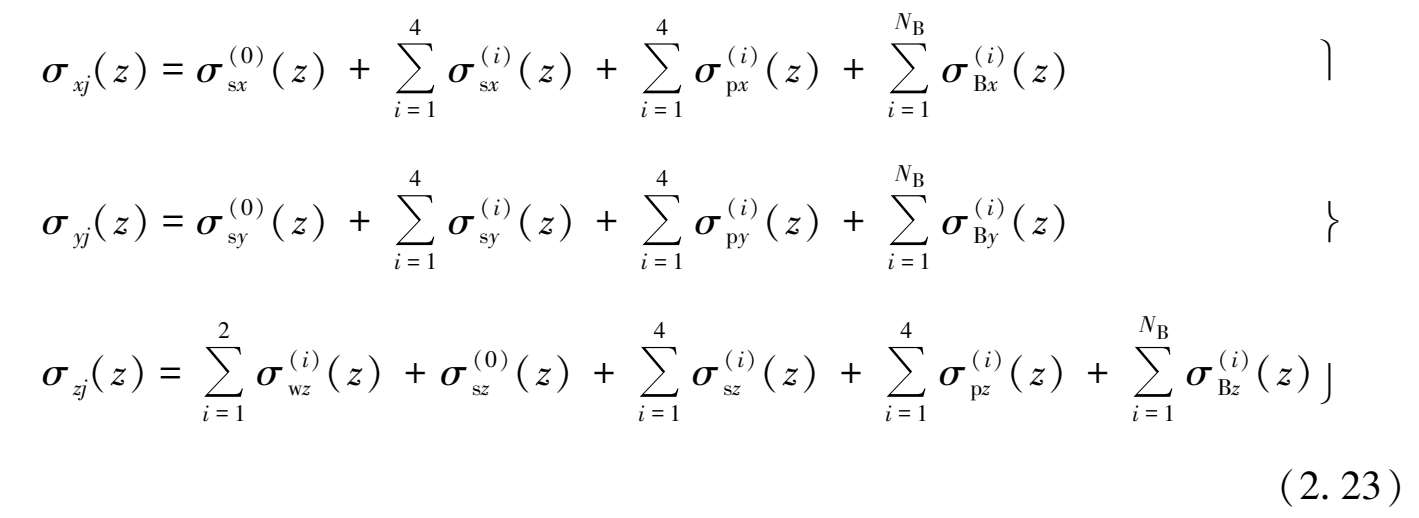
根据上述计算原理,求解出土体附加应力分量σ xj (z)、σ yj (z)和σ zj (z)之后,将应力分量代入式(2.2)中,即可求解出基坑施工引起的下卧隧道位置处土体自由位移解。
本研究采用Mindlin解作为层状地层的近似解,根据本节中对层状地层泊松比的近似处理可知,应力计算中的泊松比近似取各地层泊松比的加权平均值
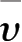 ,因此,该方法仅适用于层状土体之间泊松比变化范围不大的情况,对于土层之间参数差异较大的情况,如软弱土体与硬质基岩接触的层状地层情况下,则不推荐采用本研究方法。
,因此,该方法仅适用于层状土体之间泊松比变化范围不大的情况,对于土层之间参数差异较大的情况,如软弱土体与硬质基岩接触的层状地层情况下,则不推荐采用本研究方法。