




任何一个弹性体都是一个空间物体,任何一个实际的弹性力学问题都是空间问题。如果研究的弹性体具有某种特殊形状,并且所受的外力满足一定的条件,就可以把空间问题简化成平面问题。这样处理,分析和计算的工作量将大大减少,而所得的结果仍能满足工程精度要求。
几何特征:一个方向尺寸比另外两个方向尺寸小得多,即 t << a , t << b 。
受力特征:假设有很薄的等厚平板,在板边上受有平行于板面且不沿厚度变化的面力,同时体力也平行于板面且不沿厚度变化,此类问题就是平面应力问题。
设薄板厚度为 t ,以薄板的中面(平分板厚的平面)为 xy 面, z 轴垂直于中面,如图1-5所示,因为板面上不受力,所以有
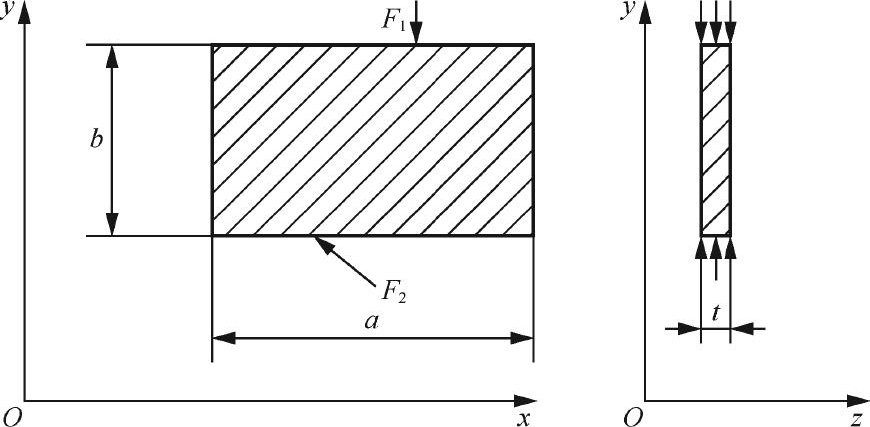
图1-5 平面应力问题
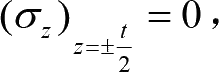
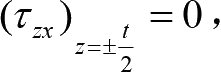
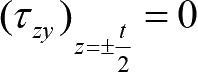
因为板很薄,外力不沿厚度变化,故可以认为整个薄板的所有点都有
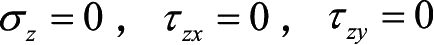
由切应力互等关系得
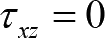 ,
,
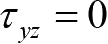 。这样只剩下平行于
xy
面的3个应力分量
。这样只剩下平行于
xy
面的3个应力分量
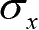 、
、
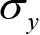 、
、
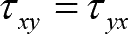 非零,所以称为平面应力问题。
非零,所以称为平面应力问题。
因为板很薄,3个应力分量、3个应变分量和两个位移分量都可以认为不沿厚度变化,即它们只是 x 和 y 的函数,与 z 无关。
几何特征:一个方向尺寸比另外两个方向尺寸大得多,且沿该方向截面尺寸和形状不变。
受力特征:设有很长的柱形体,在柱侧面上受有平行于横截面且不沿长度变化的面力,同时体力也平行于横截面且不沿长度变化,此类问题就是平面应变问题。
假想该柱体无限长,以任意一横截面为 xy 面, z 轴垂直于 xy 面,如图1-6所示,则所有应力分量、应变分量和位移分量都不沿 z 方向变化,它们只是 x 和 y 的函数。此外,在这一情况下,由于柱体无限长,任意一横截面都可看作对称面,所有点都只会沿 x 和 y 方向移动,而不会有 z 方向位移,即 w =0, ε z = γ zx = γ zy =0,不为零的应变分量只有 ε x 、 ε y 、 γ xy ,所以称为平面应变问题。
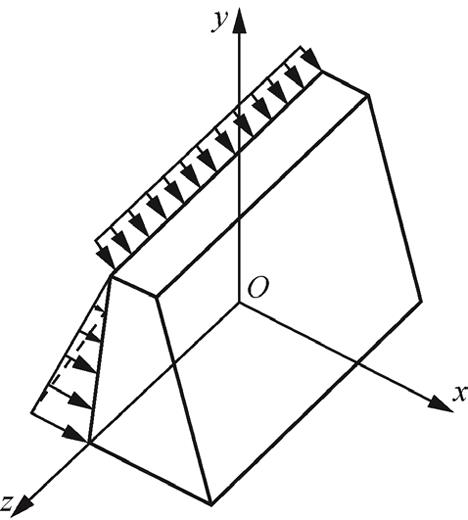
图1-6 平面应变问题
平面应力问题和平面应变问题都只有8个独立的未知量 σ x 、 σ y 、 τ xy 、 ε x 、 ε y 、 γ xy 、 u 、 v ,它们只是 x 和 y 的函数,因此统称平面问题。
平面问题的平衡微分方程为
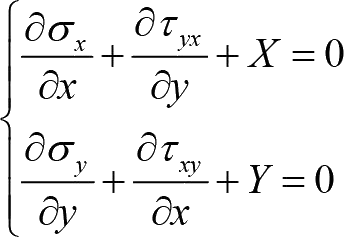 (1-14)
(1-14)
平面问题中的几何方程为
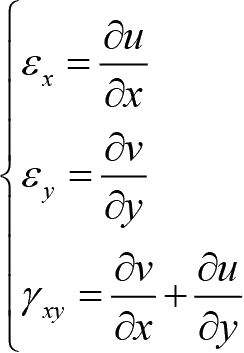 (1-15)
(1-15)
平面应力问题中的物理方程为
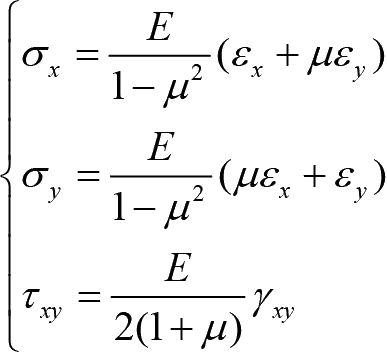 (1-16)
(1-16)
写成矩阵形式为
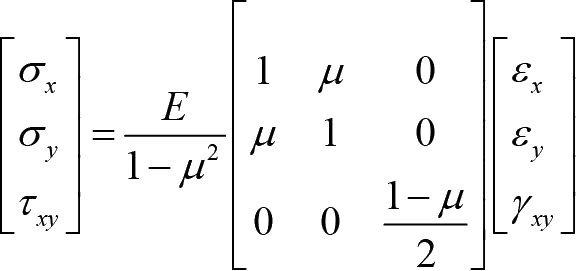 (1-17)
(1-17)
记作 σ = Dε 。其中, D 为弹性矩阵。
平面应变问题中的物理方程为
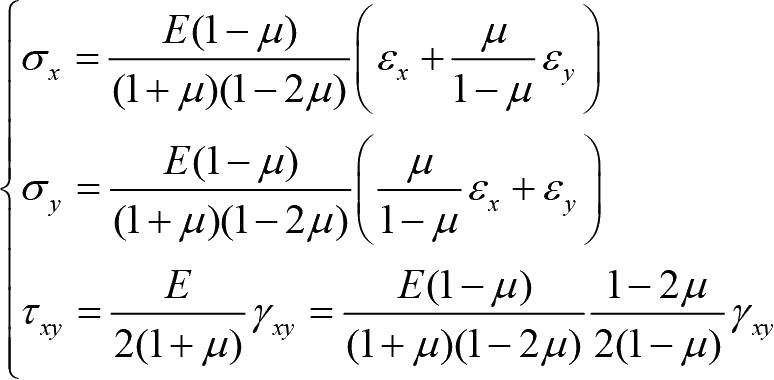 (1-18)
(1-18)
写成矩阵形式为
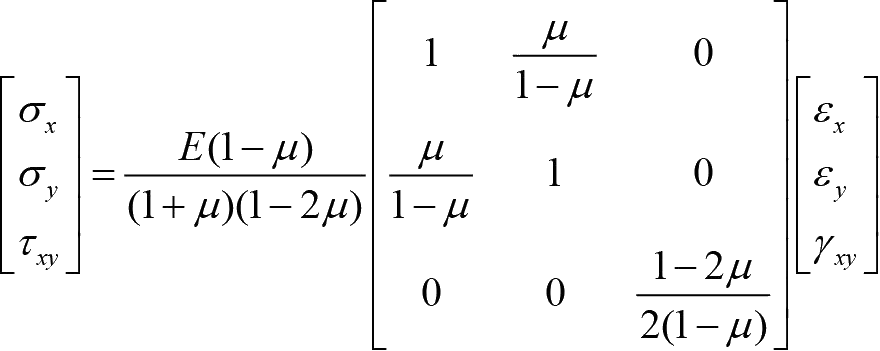 (1-19)
(1-19)
同样记作 σ = Dε 。其中, D 为弹性矩阵。
平面问题的位移边界条件为
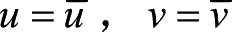 (1-20)
(1-20)
平面问题的应力边界条件为
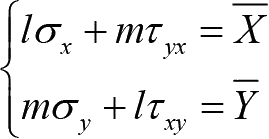 (1-21)
(1-21)