




弹性力学研究弹性体受外力作用或由于温度变化等原因而发生的应力、应变和位移。弹性体占有三维空间,描述弹性体受力和变形的应力、应变、位移等物理量都是三维坐标的函数。
弹性力学基本方程的导出可从三方面分析:静力学方面,建立应力、体力和面力之间的关系;几何学方面,建立应变、位移和边界位移之间的关系;物理学方面,建立应变与应力之间的关系。通过分析分别得到平衡微分方程、几何方程和物理方程,统称为弹性力学基本方程。
围绕物体内任意一点,取如图1-1所示的一个微小平行六面体,它的3组面平行于3个坐标面,各边长度都是微量d x 、 d y 、 d z 。外力作用下物体处于静力平衡状态,物体内任意一点也处于静力平衡状态,单元体各面上所受应力及单元体受到的体力满足平衡方程。3个力的平衡方程为
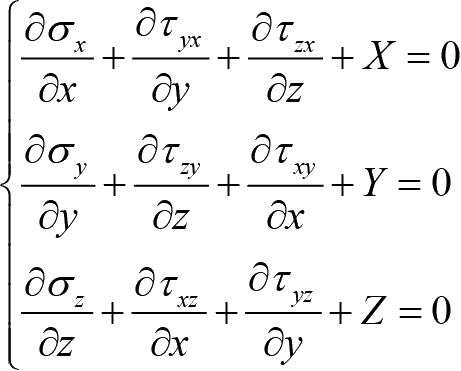 (1-8)
(1-8)
如图1-3所示,可以列出平面问题中的几何方程:
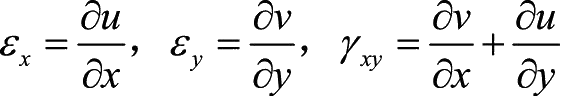 (1-9)
(1-9)
同理可得空间问题的几何方程:
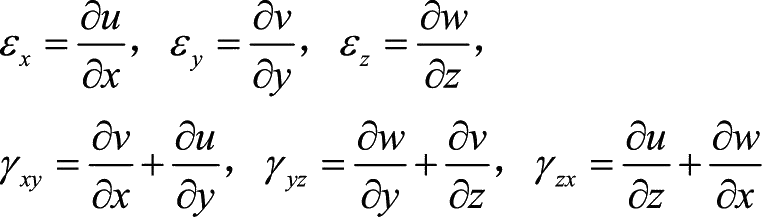 (1-10)
(1-10)
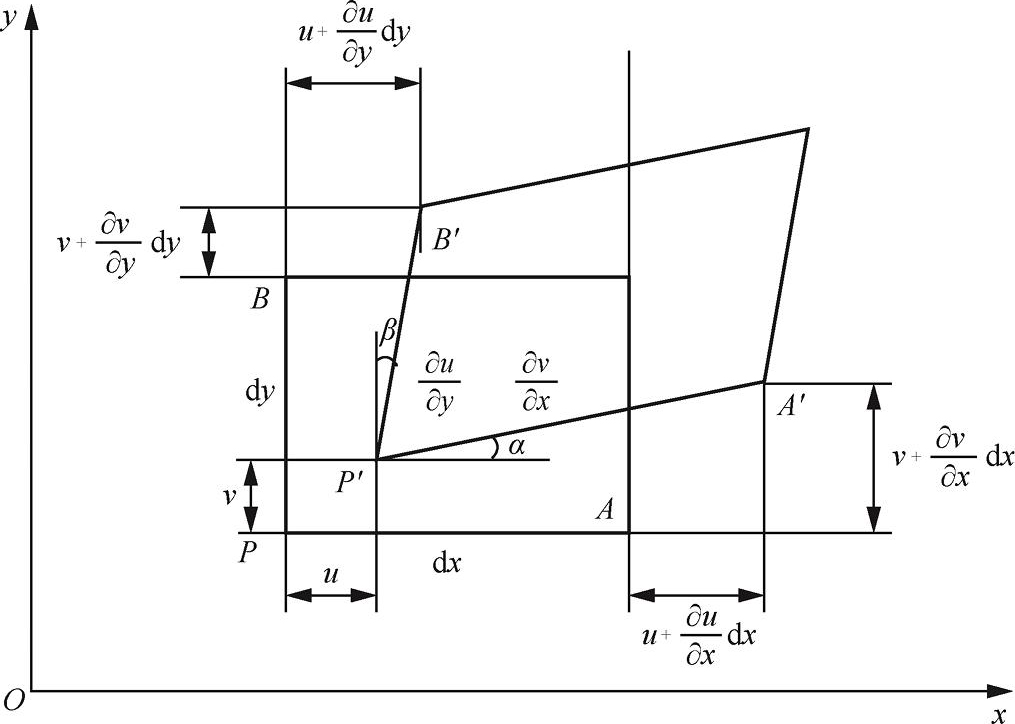
图1-3 平面应变与位移
物理方程体现了应力与应变的关系,也称为本构方程,即
 (1-11)
(1-11)
其中,
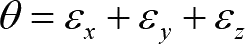 为体积应变。
为体积应变。
上述各方程均可用矩阵方程表示,如式(1-11)可用矩阵方程表示为
 (1-12)
(1-12)
简写成 σ = Dε 。其中, D 称为弹性矩阵,它完全由弹性常数 E 和泊松比 μ 决定。
弹性力学基本方程共15个,由于平衡方程和几何方程都是微分方程,求解定解还需要边界条件。根据边界条件的不同,弹性力学问题分为位移边界问题、应力边界问题和混合边界问题。
在位移边界问题中,物体在全部边界上的位移是已知的,即
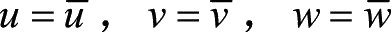
其中,
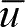 、
、
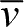 、
、
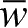 在边界上是坐标的已知函数,这就是位移边界条件。
在边界上是坐标的已知函数,这就是位移边界条件。
在应力边界问题中,物体在全部边界上的面力分量是已知的。根据面力分量和应力分量之间的关系,可以把面力已知的条件转换成应力方面的已知条件,这就是所谓的应力边界条件,即
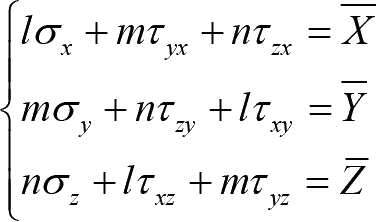 (1-13)
(1-13)
其中,面力分量
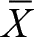 、
、
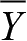 、
、
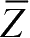 在边界上是坐标的已知函数,
l
、
m
、
n
为边界面外法线方向的方向余弦。
在边界上是坐标的已知函数,
l
、
m
、
n
为边界面外法线方向的方向余弦。
在混合边界问题中,物体的一部分边界具有已知位移,即具有位移边界条件,另一部分边界则具有已知面力,即具有应力边界条件。例如,图1-4(a)所示的固定铰支和可动铰支处为位移边界条件, DC 边界上分布面力大小为 q ,其他边界上应力为零,为面力边界条件,整个问题为混合边界问题。图1-4(b)中同一边界存在两种边界条件: x 方向位移 u | x = a =0; y 方向切应力 τ xy | x = a =0。
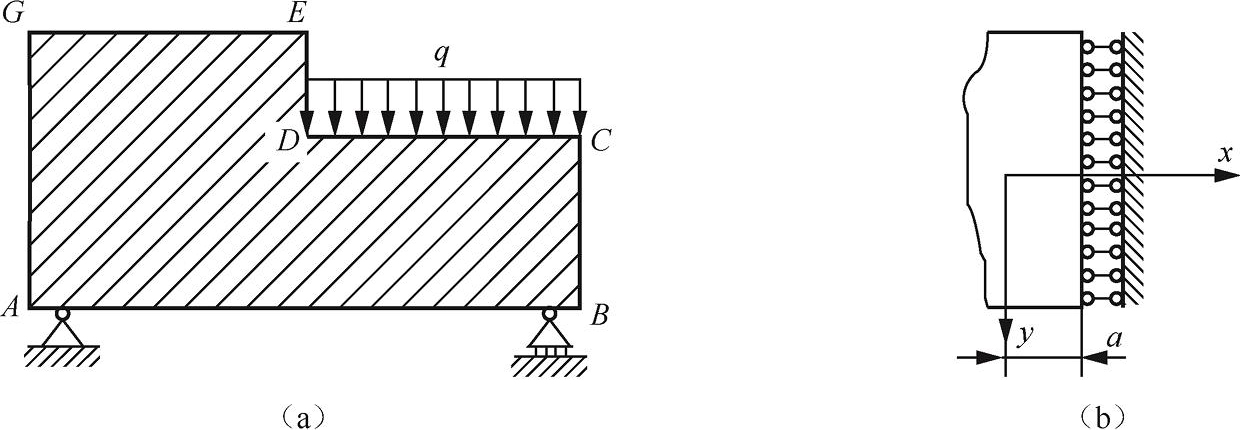
图1-4 混合边界问题