下载掌阅APP，畅读海量书库
立即打开
在本节中，我们主要介绍弹性力学中的基本概念，包括体力、面力、应力、应变、位移、主应力、相当应力和主应变。
体力是一种外载荷，是随体积分布的力，如重力和惯性力。当材料具有磁性或者分布有非自由电荷，这时磁力和静电力也是体力。体力的单位为N/m
3
。体力在三个坐标轴上的投影为
X
、
Y
、
Z
，它们的总体可用体力列阵表示：
。
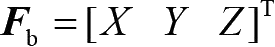面力也是一种外载荷，是作用在物体表面的力，如接触力和流体压力，其单位为N/m
2
。面力在三个坐标轴上的投影为
、
、
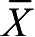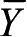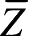，它们的总体可用面力列阵表示：
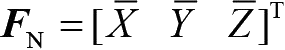。集中力也是一种面力，它作用在物体表面，忽略其作用面积，认定只作用在一点，单位为N。
应力是单位截面面积的内力（或内力的分布集度），是表示物体内某位置、沿某截面分布内力的大小和方向的物理量。物体由于外力或湿度、温度改变，其内部将产生内力。
在物体内的同一点，不同方向截面上的应力是不同的。过某点，各截面上应力的大小和方向的总和称为该点的应力状态。为了研究某点的应力状态，围绕该点取一个微小单元体，通常用与坐标面平行的平面截出微小的平行六面体，如图1-1所示，单元体三个方向上的尺寸都是非常小的，分别是d
x
、d
y
、d
z
。单元体每个面上的应力分解为一个正应力、两个切应力，分别与坐标轴平行。正应力的作用面用下标表示，如法线平行于
x
轴的面上正应力记作
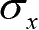；切应力有两个下标，第一个下标为作用面，第二个下标为切应力方向，如
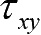表示其作用面垂直于
x
轴，方向平行于
y
轴。正应力与切应力正负号规定如下：正面上与坐标轴正方向一致为正，相反为负；负面上与坐标轴正方向一致为负，相反为正。正应力也简单记作拉为正、压为负。图1-1的单元体上，各面上的应力分量均为正。根据切应力互等定理，6个切应力有3组互等关系，即
，
，
。
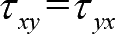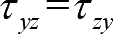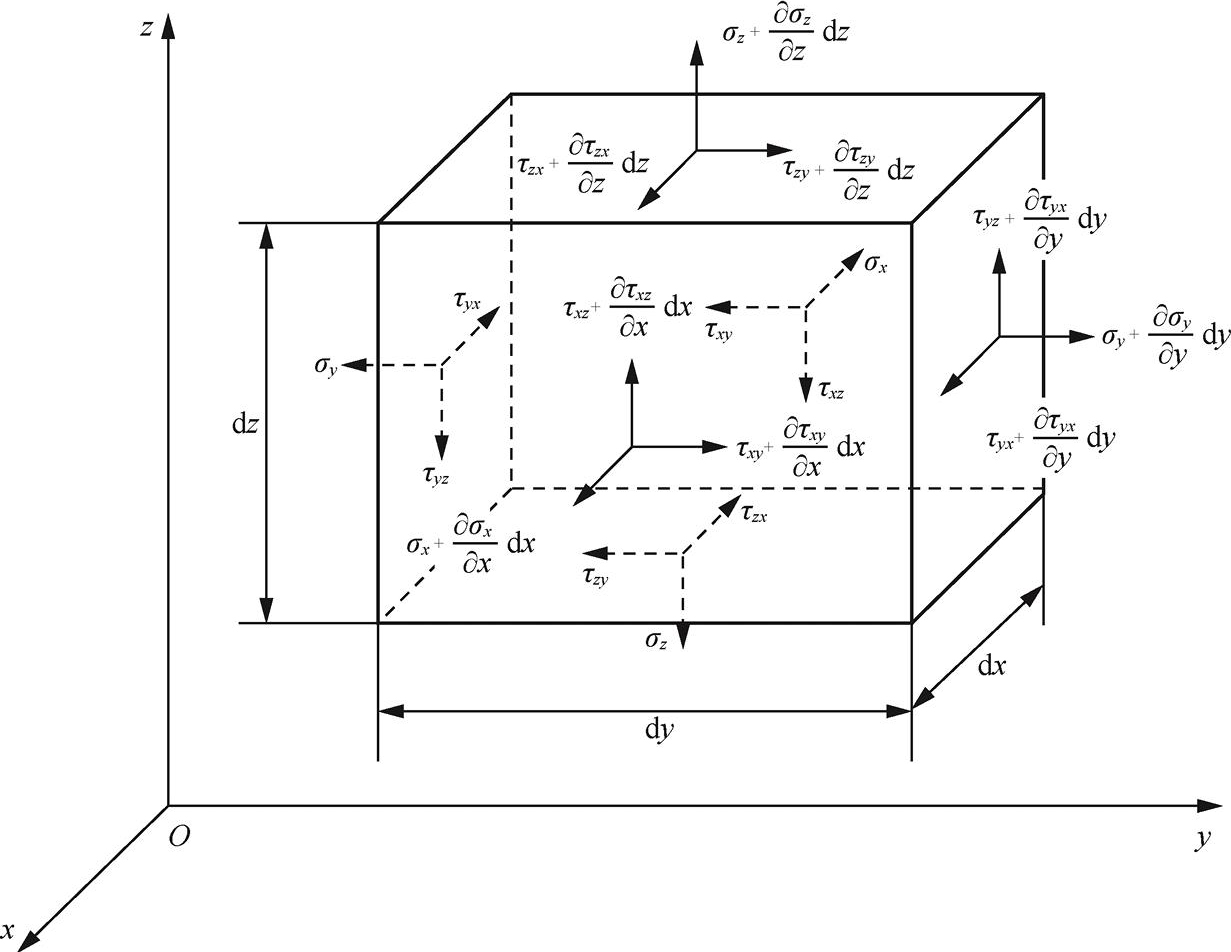
图1-1 单元体及其各面上的应力分量
物体中某点的应力状态完全可以由
、
、
、
、
、
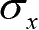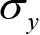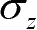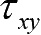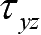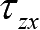6个应力分量确定，用应力阵列表示为
。
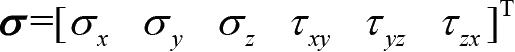应变反映弹性体在外力作用下，其内部各部分发生变形的程度。变形可以归结为长度的改变与角度的改变，故有线应变与角应变。各线段单位长度的伸缩称为正应变或线应变；各线段之间直角的改变，用弧度表示，称为切应变或剪应变。正应变用
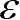表示，切应变用
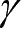表示，用下标表示应变方向，如
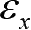表示
x
方向上的线应变，
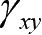表示
x
、
y
两方向的线段之间的直角改变量。正应变以伸长为正，缩短为负；切应变以直角变小为正，变大为负。正应变与切应变都是无量纲的量。由切应力互等和胡克定律，得到切应变也是两两互等的，即
，
，
。
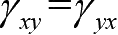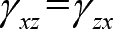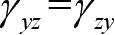物体中某点的变形状态可用
、
、
、
、
、
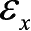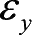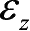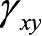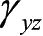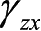这6个应变分量确定，用应变列阵表示为
。
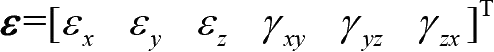位移是指物体受力过程中，物体上各点位置的变化量（位置的移动）。物体内一点（微元体）的位移由刚性位移和弹性位移两部分组成，刚性位移是由其他点的形变引起的位移，弹性位移是本身弹性变形产生的位移，与应变有着确定的几何关系。位移是一个矢量，用
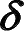表示，它在空间直角坐标系中，三个坐标方向的位移分量用
u
、
v
、
w
表示。位移分量以沿坐标轴正方向为正，沿坐标轴负方向为负。位移及其分量的单位为m，用一个位移列阵表示为
。
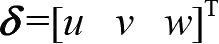主应力指的是物体内某一点的微面积元上剪应力为零时的法向应力。这时，法向量 n = ( n 1 ， n 2 ， n 3 )的方向称为这一点的应力主方向。
弹性体在外力作用下是否会破坏要通过应力来判断，有限元计算的直接应力结果是各点的6个应力分量，其中3个主应力是判断该点材料是否破坏的主要参数。对于不同的失效形式，适用不同的强度理论。根据这些强度理论求得某点的相当应力，用以判断该点强度是否足够。下面介绍几种常用的强度理论及其相当应力。
（1）第一强度理论（最大拉应力理论）。当材料发生断裂且受力弹性体内的某点有拉应力存在，即 σ 1 大于零时，可以按照该点最大拉应力 σ 1 是否小于许用应力来判断该点强度是否足够。第一强度理论的相当应力为
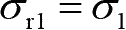（1-1）
（2）第二强度理论（最大拉应变理论）。当材料发生断裂且受力弹性体内的某点没有拉应力存在，即 σ 1 小于零时，可以按照该点最大拉应变是否小于许用值来判断该点强度是否足够。经过变换得到用主应力表示的第二强度理论的相当应力为
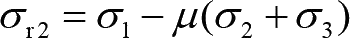（1-2）
（3）第三强度理论（最大切应力理论）。当材料发生屈服，受力弹性体内的某点最大切应力大于某一定值时，根据第三强度理论，经过变换得到用主应力表示的相当应力为
（1-3）
（4）第四强度理论（最大形状改变比能理论）。当材料发生屈服，受力弹性体内的某点形状改变比能大于某一定值时，根据第四强度理论，经过变换得到用主应力表示的相当应力为
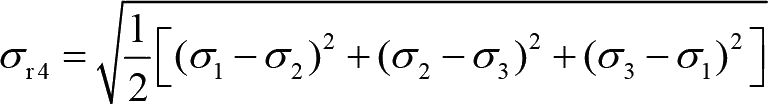（1-4）
（5）莫尔强度理论。对于一些材料，如铸铁、混凝土等，它们的抗拉能力和抗压能力不同，当它们受到剪切作用、发生剪切破坏时，不仅与切应力大小有关，还与剪切面上的正应力有关，遵从莫尔强度理论，其相当应力为
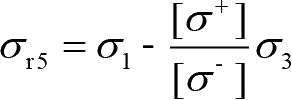（1-5）
根据这些强度理论，只要判断某点的相当应力是否小于相应材料的许用应力即可判断该点强度是否足够。
由单元体6个应变分量 ε x 、 ε y 、 ε z 、 γ xy 、 γ yz 、 γ zx ，可以求出过该点任意方向的线应变和任意两线段之间角度的改变，表达式如下。
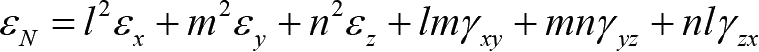（1-6）
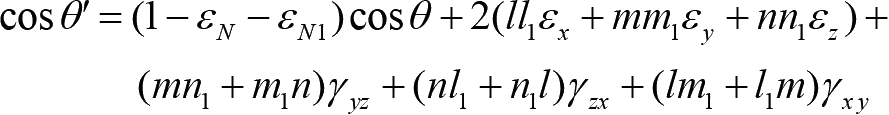（1-7）
其中， l 、 m 、 n 为过物体内某点 P 的线段 PN 的方向余弦， l 1 、 m 1 、 n 1 为过 P 点与 PN 成 θ 角的线段 PN 1 的方向余弦， θ' 为物体受力变形后线段 PN 与 PN 1 的夹角，如图1-2所示。
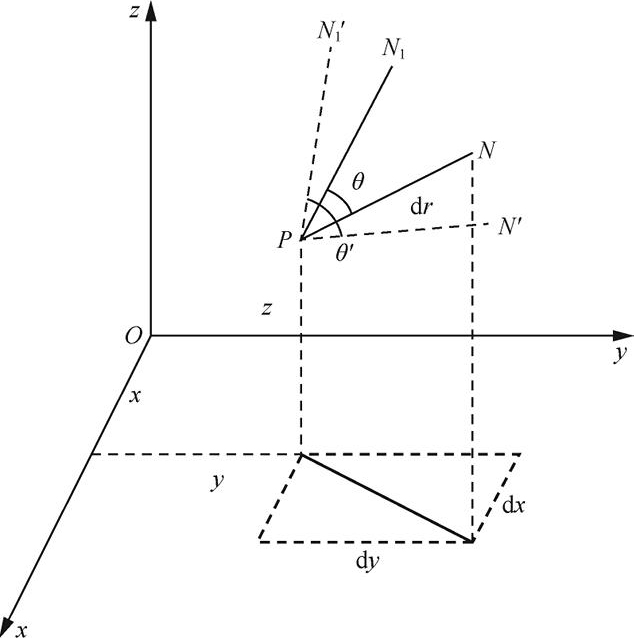
图1-2 过物体内某点 P 的线段 PN 和 PN 1
进一步分析还可知，物体内任意一点，一定存在3个相互垂直的应变主向，这3个方向的应变称为主应变。3个主应变中最大的一个就是该点的最大线应变，3个主应变中最小的一个就是该点的最小线应变。3个应变主方向与3个应力主方向是重合的，在线弹性范围内，主应力、主应变服从胡克定律（见后续的物理方程）。