




弹性力学中的三大类变量为位移、应变和应力,三大类方程是平衡方程、几何方程和物理方程。一般求解弹性力学问题的方法包括以位移为基本未知量的位移法,以应力为基本未知量,通过假设应力函数进行求解的逆解法和半逆解法。一般来说,能够直接进行解析求解的弹性力学问题相当少,而绝大多数弹性力学问题的求解需要借助于数值解法。有限元法为偏微分方程(组)提供了有效的数值近似求解手段,是数值求解弹性力学问题的重要途径。目前,大多数商业有限元软件在对弹性力学问题的分析中采用了按位移求解的方法。
有限元分析的基本步骤主要包括前处理、求解和后处理三个阶段。前处理阶段是将问题的求解域离散成有限个结点和单元,以结点的某些物理量作为基本未知量(在弹性力学问题中,一般是结点的位移),对单元进行分析,构造描述单元物理属性的形函数,描述每个单元的解答并建立起单元刚度矩阵,组装单元,形成总体刚度矩阵,并施加载荷、边界条件和初值条件;求解阶段一般是求解大型稀疏线性方程组,得到各个结点的位移值;后处理阶段是在得到结点的位移值后,进一步计算应力、应变、主应力、相当应力等,例如考虑屈服的强度问题中所需的von Mises应力等。下面通过一个简单的实例向读者逐步说明有限元求解的各个具体步骤。
假设有一个如图1-7所示的变截面直杆,其一端承受10kN集中力,上端的横截面积为100mm 2 ,下端的横截面积为50 mm 2 ,杆的长度为1m,弹性模量为 E =200GPa,利用有限元法分析沿杆长度方向上不同点变形的大小及其轴向应力(忽略杆件的自重)。
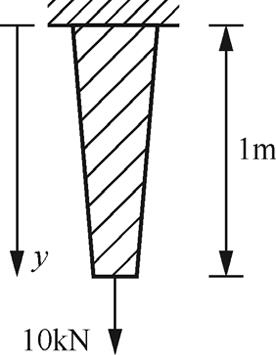
图1-7 变截面直杆
(1)单元离散。离散化为有限个结点和单元,简单起见,我们将变截面杆离散化为4个单元、5个结点,如图1-8(a)所示(说明:理论上离散的结点和单元数越多,结果可能越精确,但带来的计算量也随之增大)。
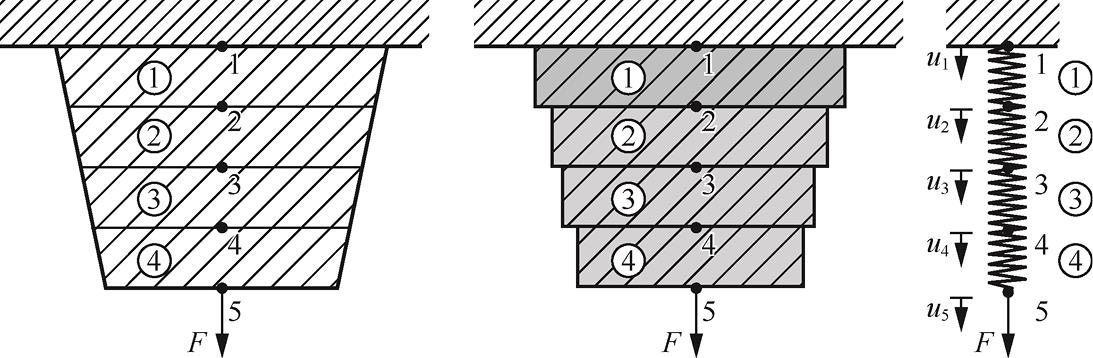
(a) (b) (c)
图1-8 将杆离散化成单元
(2)材料力学描述。假定一个近似描述单元特性的解。对于横截面积为 A ,长度为 l ,弹性模量为 E 的等截面直杆,在受到轴向力 F 的作用下且材料处于线弹性阶段时,由材料力学可知:
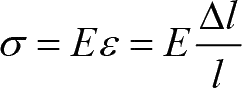 (1-28)
(1-28)
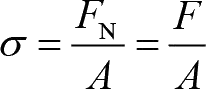 (1-29)
(1-29)
其中,
σ
是杆件横截面的正应力,
ε
是杆件横截面的正应变,
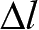 是杆件的伸长量,
F
N
是横截面上的轴向内力。
是杆件的伸长量,
F
N
是横截面上的轴向内力。
类比线性弹簧的控制方程 F = kx ,将方程式(1-28)和式(1-29)合并为
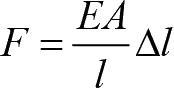 (1-30)
(1-30)
取等效刚度
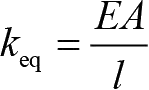 。由于直杆在
y
方向上横截面积是有变化的,作为近似,可以将该杆件看作一系列受到轴向载荷作用的具有不同横截面积的阶梯杆,如图1-8(b)所示,亦可以看作由4根具有不同等效刚度的弹簧串联而成的模型,如图1-8(c)所示。
。由于直杆在
y
方向上横截面积是有变化的,作为近似,可以将该杆件看作一系列受到轴向载荷作用的具有不同横截面积的阶梯杆,如图1-8(b)所示,亦可以看作由4根具有不同等效刚度的弹簧串联而成的模型,如图1-8(c)所示。
设第 i 个结点的位移是 u ,结点1的约束力为 F R ,对各个结点进行受力分析,如图1-9所示。建立平衡方程如下:
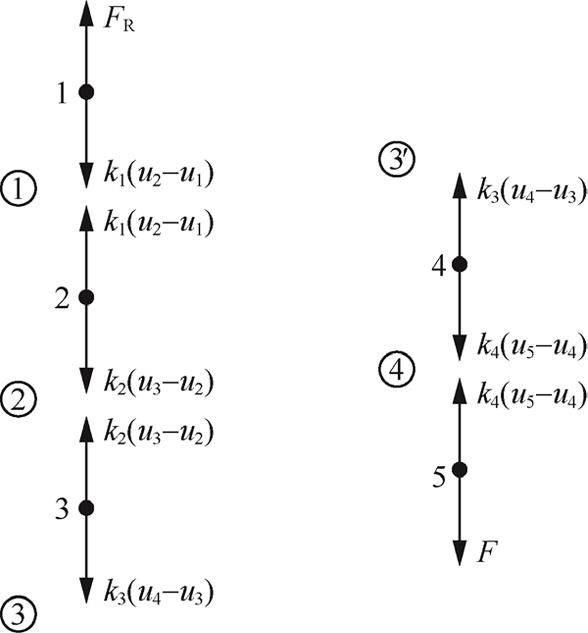
图1-9 结点受力分析
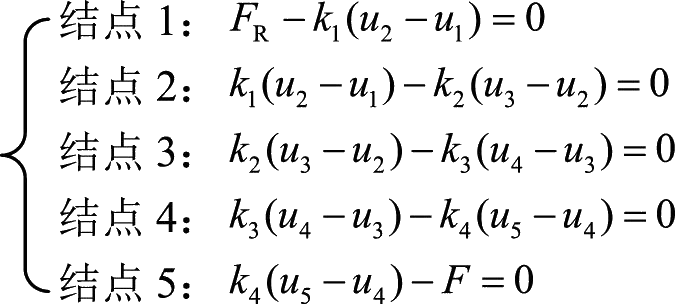 (1-31)
(1-31)
其中, k 1 、 k 2 、 k 3 、 k 4 分别表示4个单元的等效刚度。
将式(1-31)重组,并改写成矩阵形式,分离出载荷和约束力,则有
 (1-32)
(1-32)
为了不同时考虑未知的约束力和位移,我们将已知结点1的零位移,即用 u 1 =0取代方程式(1-32)的第一行,将式(1-32)改写为
 (1-33)
(1-33)
式(1-33)也可表示为
KU = F (1-34)
其中, K 是系统的整体刚度矩阵, U 是结点位移矩阵, F 是载荷矩阵。式(1-33)中的5个方程包含5个未知量,可以求出全部的结点位移,然后可以利用式(1-32)求出约束力。
(3)单元刚度矩阵。前述方法直接求出了系统的整体刚度矩阵,若分析其中的一个单元,则会发现这种单元只有轴向力的作用,对任一结点只有一个轴向位移。考虑弹簧单元内力和位移的关系,根据图1-10所示第 i 个结点和第 i +1个结点的单元内力 f i 和 f i +1 ,有
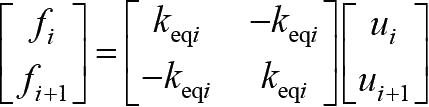 (1-35)
(1-35)
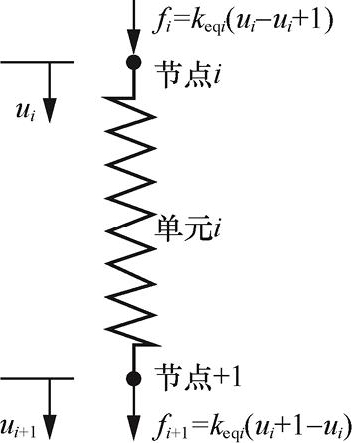
图1-10 弹簧单元
列向量
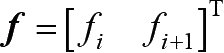 称为单元的结点力向量,矩阵
称为单元的结点力向量,矩阵
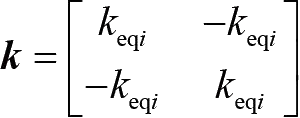 称为单元刚度矩阵,列向量
称为单元刚度矩阵,列向量
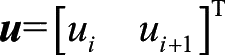 称为单元的结点位移列阵。这三者亦有如下关系:
称为单元的结点位移列阵。这三者亦有如下关系:
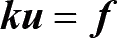 (1-36)
(1-36)
(4)单元组装。将式(1-35)所描述的单元刚度方程应用到所有单元,并将它们组合成整体刚度矩阵
K
。以单元②为例,该单元连接结点2和结点3,因此
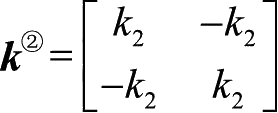 。用
k
(2
G
)
表示单元②进行扩展后的矩阵,用以进行单元刚度矩阵的组装,也能够清晰地看出单元②在整体刚度矩阵中的位置:
。用
k
(2
G
)
表示单元②进行扩展后的矩阵,用以进行单元刚度矩阵的组装,也能够清晰地看出单元②在整体刚度矩阵中的位置:
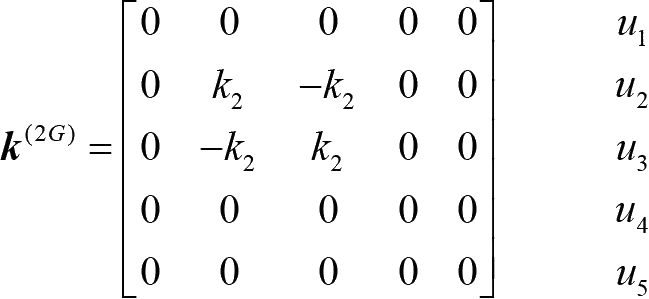
通过在单元刚度矩阵的右边列上结点位移,可以帮助观察该结点对临近单元的影响。同样可以写出单元③扩展后的矩阵:
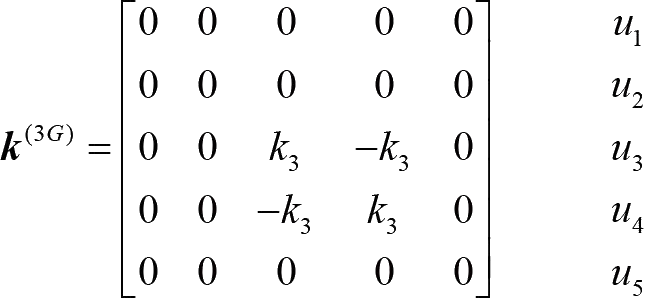
将各个单元在整体刚度矩阵中的位置进行组合,即对扩展后的矩阵相加,得到最后的整体刚度矩阵 K :
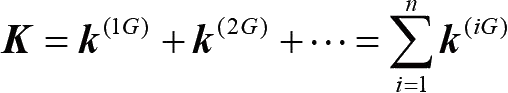 (1-37)
(1-37)
其中, n 表示单元的总数,这里 n =4。
因此,整体刚度矩阵可显式地写为
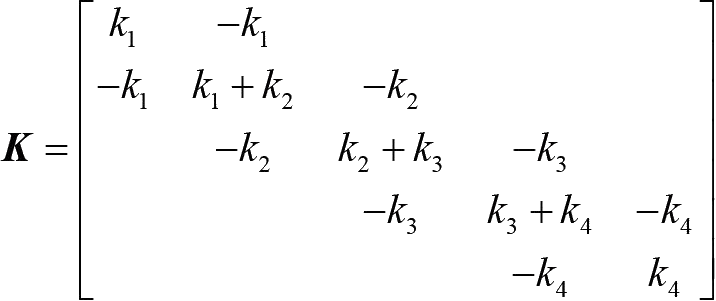 (1-38)
(1-38)
此式与式(1-32)的刚度矩阵一样。有了整体刚度矩阵以后,我们就可以施加边界条件,并进一步根据式(1-34)进行求解。
假定各单元的长度相等,并以单元的平均横截面积作为单元的计算截面面积,计算等效刚度
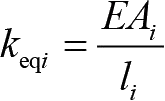 。各单元属性见表1-1。
。各单元属性见表1-1。
表1-1 单元属性
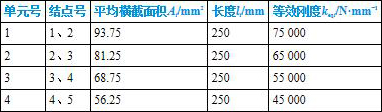
根据式(1-38)算出整体刚度矩阵,有
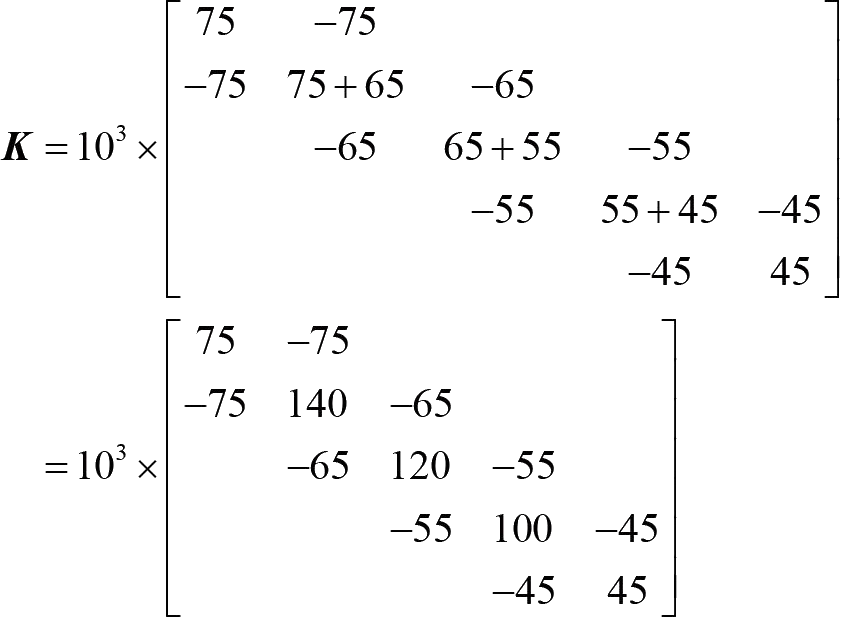
引入边界条件 u 1 =0, F =10×10 3 N,根据式(1-33),有

划去第一行和第一列,只需要求解4×4的矩阵方程:

解得: u 2 =0.133 333 mm, u 3 =0.287 179 mm, u 4 =0.468 998 mm, u 5 =0.691 220 mm。
每个单元的平均应力可按式(1-39)计算:
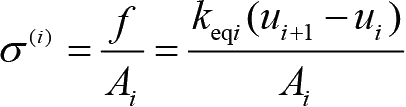 (1-39)
(1-39)
代入位移计算结果后,求得
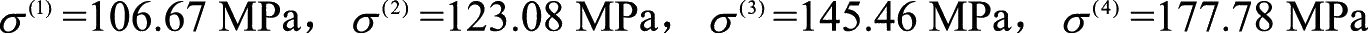
无论在何处截断杆件,截面的内力都是
F
N
=10 000 N,因此对于每个单元,可以利用已知材料力学公式
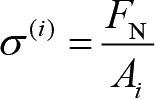 进行验证。结果表明,通过位移信息计算得到的单元应力和采用材料力学公式计算得到的单元应力完全相同,因此就本问题而言,位移计算是正确的。同样也可将结果代入式(1-32),求出约束力
F
R
=10 000 N=10kN,显然该结果与整体平衡条件相符。
进行验证。结果表明,通过位移信息计算得到的单元应力和采用材料力学公式计算得到的单元应力完全相同,因此就本问题而言,位移计算是正确的。同样也可将结果代入式(1-32),求出约束力
F
R
=10 000 N=10kN,显然该结果与整体平衡条件相符。
说明:这里计算的应力是单元的平均应力,并不是指结点的应力,在有限元法中,经常把与结点相关联的单元的应力进行平均作为结点的应力值。