




在第一章已经表明,人口老龄化程度是用老年人口比重这一变量体现的,用老龄化率
α
R
表示。而劳动力的赡养负担是用老年供养比这一指标表示的,老年供养比即老年人口数量与劳动年龄人口数量之比。根据第一章的式(1-14)和式(1-15),若
N
L
为劳动年龄人口数、
N
R
为老年人口数,则
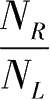 为老年赡养比。
为老年赡养比。
人口老龄化程度上升同增加劳动力的赡养负担是正向关系的。对此可进行下面的数学式变换而清晰地展现:
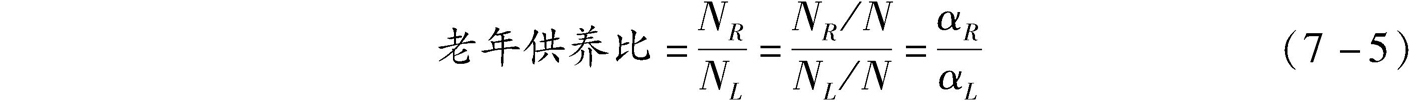
在式(7-5)中, α R 表示老年人口占总人口的比重,即老龄化率。可见,当 α L 既定时,即劳动年龄人口既定时,老年供养比和老龄化率 α R 呈正向关系。因此,老龄化率 α R 上升即导致老年供养比上升,意味着劳动力的赡养负担加重。劳动力的赡养负担加重也不利于劳动投入增加。例如,当一个家庭中有需要人照护的老年人时,家庭中劳动力的负担加重,有可能减少外面劳动的时间,而不得不花费相对更多的时间来照护家庭中的老年人。而这种微观效应的宏观结果,就是减少总体的劳动投入。
当一个国家或地区的法定退休年龄一经确定,则该社会的劳动年龄人口数量在法定方面便是被确定的。但是,一旦退休年龄被确定,劳动年龄人口数量的变动便是由生育率的情况决定的。虽然老年人口是在劳动年龄人口之前的人,理论上并不影响劳动年龄人口的数量,但是从人口结构的相对角度看,即相对于老年人口而言,与人口老龄化对应的是劳动年龄人口比重是相对下降的。同时,人口老龄化对应老年供养比的提高,即加重劳动力的赡养负担,因此相对甚至绝对影响劳动者的工作时间,因而对劳动投入产生影响。
但是,如果劳动者个人有对预期寿命不断延长的预期,则此人在从业工作期间增加工作时间,以获取更多收入而进行养老储蓄。这便是人口老龄化也导致劳动投入增加的内在机制。而这种内在机制,不是通过增加劳动者的人数实现的,而是通过增加劳动者的劳动工作时间来实现的。现假设 β 是经济中的劳动参与率,即经济中的实际劳动力数量由下面关系式决定:
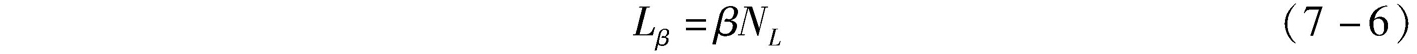
式(7-6)中, L β 表示劳动参与率为 β 情况下的实际劳动力数量(实际从业人员数量)。如果假定这些劳动力是同质的,那么 L β 也体现劳动时间的总和,即劳动投入。如果假定了每个劳动力每小时的劳动效果是一致的,那么劳动投入的多少就取决于劳动者数量的多少。
现假定 γ 表示劳动投入时间系数。 γ =1表示劳动力的劳动时间是相同的情况,并设定这是标准的情况。假定 γ >1时表示劳动力的劳动时间超过了标准情况。如假设标准情况是劳动力每天工作8小时,实际劳动时间为每天9小时,则 γ =9/8=1.125。如果实际劳动时间为每天7小时,则 γ =7/8=0.875。因此,考虑到实际劳动时间因素的劳动投入表达式为:
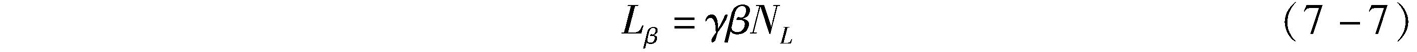
人口老龄化的微观效应是个人预期寿命延长。如果个人预期其寿命是延长的,那么可能产生激励劳动力在从业期间增加工作时间,以获取更多收入而进行养老储蓄。则对此行为对应的结果是 γ >1的情况出现,这时意味着由式(7-7)决定的劳动投入是增加的。可见,人口老龄化可以产生劳动力对寿命延长的预期而增加劳动投入的效应。
注意,上述结论是在其他条件不变的情况下得出的结论。如果劳动年龄人口是减少的,则对劳动投入是增加还是减少,取决于 γ 增加和 N L 减少二者相抵后的结果的情况。
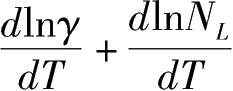
对式(7-7)两边取对数,并求关于时间 T 的导数,得到下面的表达式:
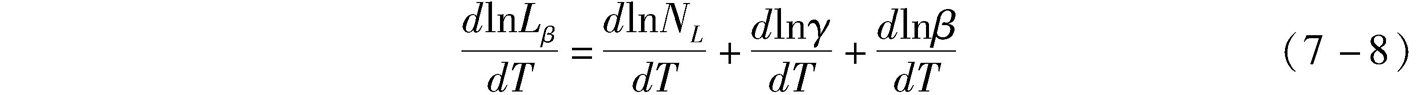
显而易见,式(7-8)中
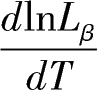 为劳动投入增长率。式(7-8)表明,劳动投入的增长率同三个因素有关,一是劳动年龄人口数量增长率
为劳动投入增长率。式(7-8)表明,劳动投入的增长率同三个因素有关,一是劳动年龄人口数量增长率
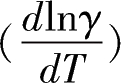 ,二是劳动投入时间系数增长率
,二是劳动投入时间系数增长率
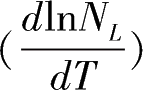 ,三是劳动参与率增长率
,三是劳动参与率增长率
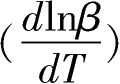 。
。
因此,如果假设劳动参与率
β
不变,则
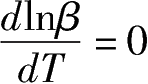 。于是,在此情况下,劳动投入增长率
。于是,在此情况下,劳动投入增长率
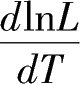 是正值还是负值,取决于
是正值还是负值,取决于
 是大于零还是小于零。例如,如果每个劳动者的劳动时间从每天8小时提高到9小时,则劳动时间系数增长率为12.5%。因此,如果
是大于零还是小于零。例如,如果每个劳动者的劳动时间从每天8小时提高到9小时,则劳动时间系数增长率为12.5%。因此,如果
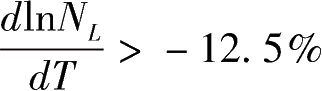 ,即劳动年龄人口增长率不低于-12.5%时,劳动者延长劳动时间的结果会导致总劳动投入增加。可见,如果劳动者每天从工作8小时提高到9小时,即每天增加1个小时的劳动时间的效应是较大的。
,即劳动年龄人口增长率不低于-12.5%时,劳动者延长劳动时间的结果会导致总劳动投入增加。可见,如果劳动者每天从工作8小时提高到9小时,即每天增加1个小时的劳动时间的效应是较大的。
生育率下降也是导致出现人口老龄化的重要原因。在实现经济中,老龄年龄人口决定不了劳动年龄人口,但是未成年人口是决定劳动年龄人口的变量。由于未成年人是成年人的前期基础,因此生育率下降意味着在未来一定时期内劳动年龄人口的增加是减缓的。这是因为生育率下降,会导致新出生人口减少,意味着在一定时期后进入劳动年龄人口的数量将减少。总的来看,如果人口老龄化伴随着生育率下降,最终导致经济中的劳动年龄人口减少,从而对应劳动投入减少是符合逻辑关系的。