




这不是一根管子。(Ceci n’est pas une pipe.)
——劳伦特·陶丁根据福柯《这不是一支烟斗》( This Is Not a Pip e )中勒内·马格里特(René Magritte)的画作《图像的反叛》( The Treachery of Images )绘制的图画
外部表征是一种思想工具,它在物质世界和想象世界之间进行调解,也创造了自己的现实。
 在本章中,我将考虑知识史上的四个重要例子,用它们来说明外部表征对于知识系统转型的关键作用。
在本章中,我将考虑知识史上的四个重要例子,用它们来说明外部表征对于知识系统转型的关键作用。
 这些例子还将用于说明外部表征的不同类型,从符号系统到图表(diagram)。前两个例子涉及古代美索不达米亚文化中算术和文字的出现。第三个例子涉及化学式的发明。第四个例子则说明了在对变化过程进行量化时,图表在塑造概念系统中的作用。在所有这四个例子中,每种外部表征带来的转型都对知识史产生了持久影响。即使在今天,在我们书写,计算,描述化学反应,或理解变化过程的方式中,也可以发现它们的影响。
这些例子还将用于说明外部表征的不同类型,从符号系统到图表(diagram)。前两个例子涉及古代美索不达米亚文化中算术和文字的出现。第三个例子涉及化学式的发明。第四个例子则说明了在对变化过程进行量化时,图表在塑造概念系统中的作用。在所有这四个例子中,每种外部表征带来的转型都对知识史产生了持久影响。即使在今天,在我们书写,计算,描述化学反应,或理解变化过程的方式中,也可以发现它们的影响。
戴培德与他的同事对古代美索不达米亚地区文字和算术的出现进行了研究,他们的研究成果对于理解外部表征在抽象概念历史起源中的作用具有典范性。
 因此,我对历史案例的研究从算术和文字的出现开始。我打算说明外部表征在抽象数字概念的产生中的作用,以及在从早期情境依赖的会计和管理形式演变到适合代表口语的文字系统中的作用。
因此,我对历史案例的研究从算术和文字的出现开始。我打算说明外部表征在抽象数字概念的产生中的作用,以及在从早期情境依赖的会计和管理形式演变到适合代表口语的文字系统中的作用。
实际上,当文字和算术在公元前4千纪的城市革命期间出现时,并没有立即产生抽象的数字或通用的文字系统,而是产生了适合特定情境和管理活动的心智模型的技术。这些心智模型的出现与符号系统的发展紧密相关,而符号系统被用于协调复杂社会中的人类集体行动。正如我们将要看到的,数字抽象概念和通用文字系统的出现遵循着我们在上一章已经熟稔的顺序:变革的诱因(在本例中是管理型经济的扩张)、对现有外部表征可能性的探索,以及对最初只是以会计实践为核心的知识系统的重组。

因此,让我们利用前面两章介绍过的理论工具箱,更细致地思考这个重要例子。用名称、符号或筹码来标识具体对象就创建了该对象的一阶表征。然后,这些表征就可以按照与对象本身几乎相同的方式来处理,例如,它们可以连接或分离,也可以按顺序排列。从历史上看,最早的算术活动形式是使用具体物体或符号的标准系列作为对象的一阶表征,这些一阶表征与对象是一一对应的关系。然后可以通过筹码的重复来代表一组对象的数量。当按时间顺序将标准化的词语序列分配给特定集合中顺序固定的元素时,计数序列就出现了。它代表特定集合的所谓“序数”结构。
在这种可以被描述为“原算术”(protoarithmetical)的初始思维水平上,并没有对应于算术运算(如加法或乘法)的符号性转换。符号性转换仅被用于对象本身的表征,而不是更高阶认知结构的表征,后者体现了更抽象的数字概念。在许多留存下来的无文字文化中都发现了原算术的思维形式。在历史上,它们更难证明,但或许可以追溯到定居农业种植和畜牧业的开始。
但在美索不达米亚平原和波斯高地上,已经发现了可以追溯到公元前8千纪初的黏土代币。可以想象,这些形状各异的黏土代币可能已被用作对象的一阶表征,并在原算术计数和核算的背景下用于代表和控制对象的数量。

早期文字大事年表

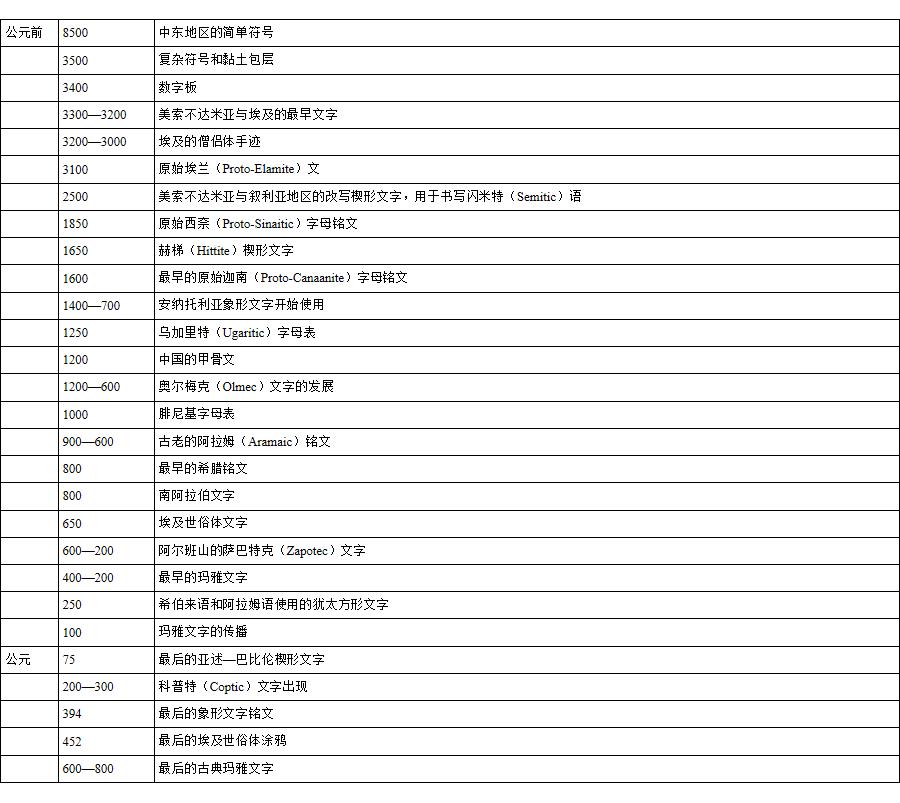
数字概念与算术思想大事年表 [1]
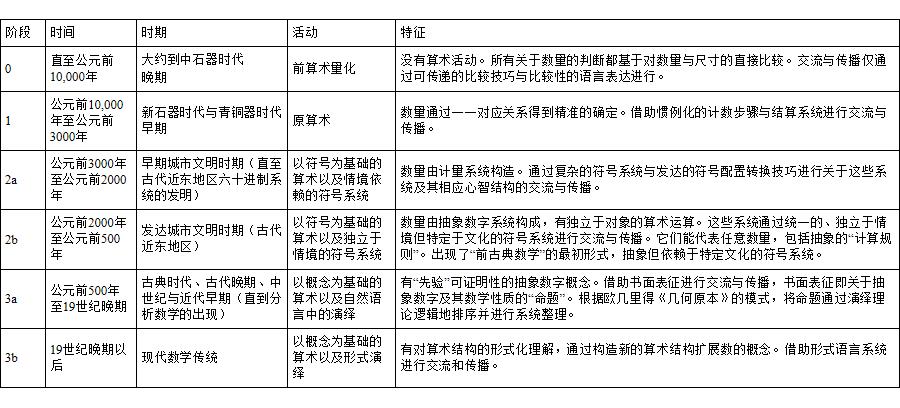

图5.1 空心黏土球的样子,其中包含用于计数的小代币。其历史可以追溯到大约公元前3500年至公元前3300年。德国考古博物馆藏,伊姆加德·瓦格纳(Irmgard Wagner)拍摄
在公元前4千纪后半叶,旧的外部表征形式得到改造和重新利用。在美索不达米亚平原的农村经济背景下发展起来的适度结算技术,在新兴城邦的管理中得到了广泛利用。可证实的最早筹码包含捆绑在一起的高阶单位(6、10、60),它们本身就表明了对一物一代币关系的解放。传统结算技术中出现了代表某些行政行为的印章,例如记录工人的劳动量或为他们提供的食物。在经济增长的背景下,对这些管理知识的外部表征的探索最终导致了传统符号文化的转变。符号表征工具的潜力已被开发到了极限——这是之前讨论过的知识演化的特征。这一点在结算实践的剧增中尤其明显,结算实践在农村社区中原本只起到很小的作用。
此前,用于结算的符号基本上仍然是关于数量和管理或经济实践的一阶表征。但是,它们现在成了发达符号系统的一部分,并被用于更复杂的管理目的。它们不代表抽象数值;相反,它们的含义和数值取决于语境,即它们所计数的内容。同时,符号性转换并不代表真实行为;它们仅用于说明符号系统生产与结算环境相关知识的潜力。
当传统结算技术的两个主要要素——用于记录管理对象数量的筹码和记录相关行政行为的印章印记——被某种单一媒介所代表时,历史就来到了一个关键的转折点。特别是印章,它们带有决定其含义的行政和社会背景信息。它们为财产、法律行为或社会上的正确行为作证。最初,这两种要素以密封的空心黏土球(“大泡”,bullae)形式整合在一起,它们传达出黏土筹码的某些组合。有时,内部代币的组合由“大泡”表面的标记表示。原则上,密封的黏土板具有相同的功能,但它们比“大泡”更易拿取。无论如何,两种最初分开的结算技术(筹码和印章)因此被整合到一种新的外部表征形式中,其巨大的潜力可以(并确实)在此后得到探索。

图5.2 乌鲁克城邦的原始楔形文字板(约公元前3000年),它展示了对生产干谷物制品和啤酒所需成分的量的计算(见下页作者手绘图)。见Nissen, Damerow, and Englund (1993, 42–43)。楔形文字数字图书馆供图
这些密封的黏土板代表着原文字和原算术的早期阶段,成为探索古代美索不达米亚社会信息存储和处理新形式的起点。例如,我在这里关注美索不达米亚历史而不是埃及算术和文字,原因之一确实是,这个最终导致了抽象数字概念和成熟文字系统的中间发展步骤拥有丰富的证据。
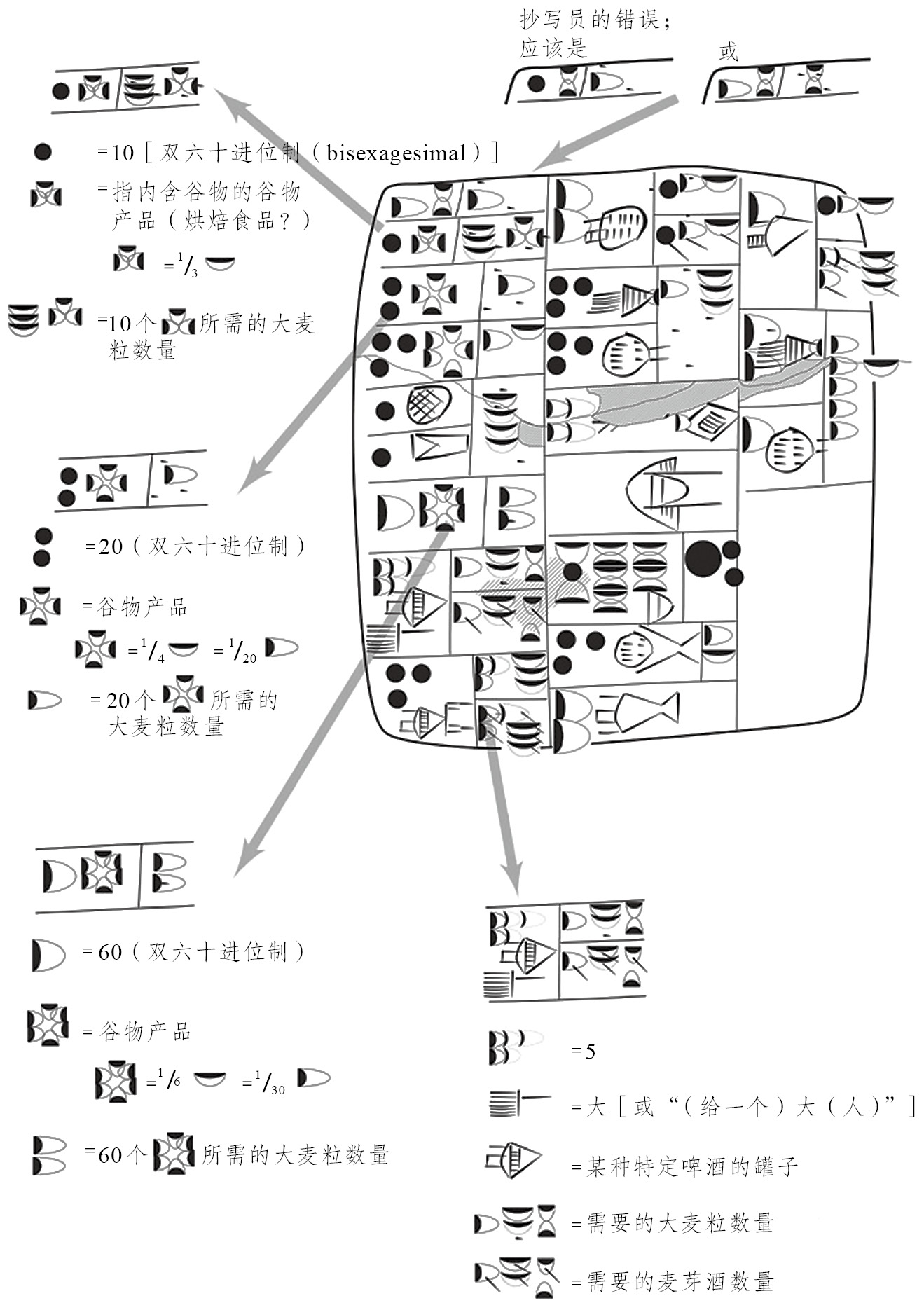
与早期管理技术相比,黏土板可以容纳更多信息,并且可以更加灵活和高效地构造信息。例如,很容易发明出表示新语义类别的新符号。反过来说,现有的经济和管理活动也被这些新的表征技术所塑造。这种发展的结果是,所谓的原始楔形文字管理文本成为行政官员积累和分配资源以及产品的心智模型的外部表征。这种心智模型又是通过反思该行政管理的具体实践而产生的。
通过反思这些原算术心智模型及其符号表征,数量和算术活动的二阶表征得以产生。尽管这些数量和算术活动最初可能保留了情境依赖性,但它们的含义不再主要由对具体对象的处理决定,而是由其一阶外部表征执行的行动确定。因此,二阶表征的特点是定义明确的数字符号系统和针对其应用的符号规则。这些形式规则直接适用于符号。形式规则可能是隐含的,也可能是明确表述的。无论如何,其应用都比较严格,也不再取决于具体世界中的偶然条件。在美索不达米亚的这个例子中有一个这样的明显阶段(对应于约公元前3200年到最晚公元前2000年的时期,即从首次出现文字到乌尔第三王朝时期末发明六十进制系统),在此期间,基于符号的算术二阶表征及其含义随情境而变化。
 在这段时期内,仍然缺乏一种标准化且能够涵盖所有领域的通用符号系统。
在这段时期内,仍然缺乏一种标准化且能够涵盖所有领域的通用符号系统。
在随后的阶段中,这种标准化确实发生了,由此产生出一种记号,所有特定于情境的表征都可以转换为这种记号。这种通用表征允许进行形式操作,而无须指向任何特定应用。在美索不达米亚的例子中,这一阶段是随着六十进制的发明(大约在公元前2050年)达到的,该系统统一了先前所有对离散对象进行计数的、情境依赖的符号系统。这在乌尔第三王朝帝国统一城邦的过程中发生,相应时期也出现了中央行政机构。由于建立了六十进制,算术也得到了统一。在这种新情况下,对算术运算的反思产生了技术术语、问题类型和解决策略,这些都成为后来被称为巴比伦数学的内容的核心。
总之,算术作为处理外部表征的一种规则系统而出现。不必假设抽象的数字概念作为其历史发展的起点。类似的发展也发生在其他文化中。在中国、埃及、印度、中美洲(Central American)和美索不达米亚等不同的文化中都出现了基于符号的算术。
 例如,中国的《九章算术》可以追溯到公元前1千纪。
例如,中国的《九章算术》可以追溯到公元前1千纪。
 这部著作提到在算板上用算筹进行计数操作。
这部著作提到在算板上用算筹进行计数操作。

这种算板成了算术运算中特定心智模型的物质模型,算筹数模拟了真实物体集合的组成和分解。在埃及算术中,这一功能由书面的象形数量符号来完成。

希腊哲学家倾向于抑制抽象知识的实践根源。柏拉图在他的《理想国》中写到了理论数学与实践数学之间的关系,他贬低后者:
因此,格劳孔,算学这个学问看来有资格被用法律规定下来;我们应当劝说那些将来要在城邦里身居要津的人学习算术,而且要他们不是马马虎虎地学,是深入下去学,直到用自己的纯粹理性看到了数的本质,要他们学习算术不是为了做买卖,仿佛在准备做商人或小贩似的,而是为了用于战争以及便于将灵魂从变化世界转向真理和实在……因所有这些缘故,我们一定不要疏忽了这门学问,要用它来教育我们的那些天赋最高的公民。 [1]
在讨论早期国家社会的大型行政机构中文字和算术的根源时,我们也不应该忘记这些行政机构帮助维持的权力机构所带来的剥削和痛苦。
 乌尔第三王朝时期(约公元前2100年至公元前2000年)的国家是集权形式的,对其所有资源进行严格控制,包括大量的国有工人。一旦长到可被剥削的年纪,儿童便被迫进入劳作过程;老年工人不得停止工作,直到丧失劳动能力。不从事国家劳作的方式要么是逃往不知所终的所在,要么是死亡。复杂的行政机构带来了许多对后来的人类历史非常重要的创新,最大限度地利用了这些劳动力。举例来说,想想在小黏土板上记录日常活动——这一做法在很多方面都预示着现代企业的时间卡和信用凭证——然后再巧妙地将收集到的信息汇总到更大的经济控制结构中去。
乌尔第三王朝时期(约公元前2100年至公元前2000年)的国家是集权形式的,对其所有资源进行严格控制,包括大量的国有工人。一旦长到可被剥削的年纪,儿童便被迫进入劳作过程;老年工人不得停止工作,直到丧失劳动能力。不从事国家劳作的方式要么是逃往不知所终的所在,要么是死亡。复杂的行政机构带来了许多对后来的人类历史非常重要的创新,最大限度地利用了这些劳动力。举例来说,想想在小黏土板上记录日常活动——这一做法在很多方面都预示着现代企业的时间卡和信用凭证——然后再巧妙地将收集到的信息汇总到更大的经济控制结构中去。
在巴比伦,文字的发展与算术的发展非常相似。
 上面提到的原始楔形文字系统的使用,最开始完全受制于它在美索不达米亚行政机构内部的功能和它的日益复杂性。但是,这种复杂性也创造出一种背景,在这种背景下,该系统的新应用能够出现,被从新的角度看待,并与主要应用范围维持一定的距离。教育就是这样一种背景。这种重新情境化是知识演化的另一普遍特征,我在前面已经将其称为“解放性逆转”。系统日益增加的复杂性需要制度支持来实现代际传递。但是,学校教育意味着将行政管理的认知手段与其直接的应用环境分开。因此,它开辟出一种视角,即这些认知手段的潜力可以不依赖于其在具体行政管理问题上应用的限制,独立地得到探索。
上面提到的原始楔形文字系统的使用,最开始完全受制于它在美索不达米亚行政机构内部的功能和它的日益复杂性。但是,这种复杂性也创造出一种背景,在这种背景下,该系统的新应用能够出现,被从新的角度看待,并与主要应用范围维持一定的距离。教育就是这样一种背景。这种重新情境化是知识演化的另一普遍特征,我在前面已经将其称为“解放性逆转”。系统日益增加的复杂性需要制度支持来实现代际传递。但是,学校教育意味着将行政管理的认知手段与其直接的应用环境分开。因此,它开辟出一种视角,即这些认知手段的潜力可以不依赖于其在具体行政管理问题上应用的限制,独立地得到探索。
因此,文字发展的下一步由在第三章中所强调的外部表征基本特性决定:外部表征的可能应用范围要比最初引入它们的特定目标更大。实际上,原始楔形文字文本代表心智结构的潜力远远超出了美索不达米亚行政管理应用的有限领域。在它最发达的形式——在约公元前2600年达到——中,它可能已经具有表征口语的可能性。

书面语反过来又成为许多其他形式知识的重要外部表征。我将在第十章讨论早期文字社会的知识经济时回到这个问题。现在,我将自己限制在一个与数学的进一步发展有关的特定例子:文字可用于对算术运算的反思结果进行编码,从而产生,例如,关于数字概念之本质的明确语言陈述,正如我们在柏拉图等古希腊哲学家的著作中发现的。对数学运算的语言编码导向了更普遍的数学命题系统,可以用线性和层级的方式在所谓的演绎结构内进行排列。
一个例子是关于偶数和奇数性质的定义和命题,这是源于古希腊且最早可以追溯到公元前5世纪的毕达哥拉斯的学说,后来又被整合到欧几里得的《几何原本》(
Elements
)中。
 通过用代表偶数和奇数的符号对运算进行语言表征,这些概念相对于符号算术特定属性的独立性大大增加。偶数和奇数的概念含义不再由最初产生这些概念的算术技术直接构成,而是由语言学技术的应用构成。这种技术的一个例子是借助定义来确定含义,例如,针对某些算术运算的可能性或不可能性来定义质数这一概念。
通过用代表偶数和奇数的符号对运算进行语言表征,这些概念相对于符号算术特定属性的独立性大大增加。偶数和奇数的概念含义不再由最初产生这些概念的算术技术直接构成,而是由语言学技术的应用构成。这种技术的一个例子是借助定义来确定含义,例如,针对某些算术运算的可能性或不可能性来定义质数这一概念。
自从知识传播可以依靠作为外部表征的文字以来,文字就包含了特定知识领域固有的术语、问题、秘诀和命题,以及对这些因素的结构化并常常是系统化的整理。在美索不达米亚地区,文字广泛传播之后,新形式的书面知识涌现出来,例如语法文本、占卜文本、各种主题列表、史学研究文本、治疗文本、天文文本等。后来,这些知识中的一些逐渐传播到古希腊,成为新的书面表征形式的主题。这些新形式又反过来成为表征知识——包括关于哲学问题和科学问题的详尽论述——的具有影响力的模型。古代知识以书面形式进行编码,这促进了复杂知识系统向其他文化传播,如叙利亚、波斯和阿拉姆世界,以及使用拉丁语的欧洲西部地区,从而刺激了新知识的产生和对这些模式的进一步阐释。

此后,文字作为语言表征的一种手段,成为大多数社会的基本特征。文字的发明表明,历史过程的偶然结果或多或少会成为社会运作和社会稳定不可或缺的前提条件,尤其是对社会的进一步发展来说。知识的演化是高度依赖路径的过程,其中每一个特定阶段的动态,不仅取决于前一阶段的结果,也取决于某些初始生物条件和生态条件的整个演化轨迹。
另一个引人注目的案例是瑞典化学家永斯·雅各布·贝采利乌斯(Jöns Jacob Berzelius,1779—1848)在19世纪初发明的化学式,这个案例由厄休拉·克莱因分析,其中,对外部表征的反思引发出新的知识结构。
 贝采利乌斯引入了化学式,如代表水的H
2
O,它们可以同时表示无机化学领域的系统化基本实验知识,以及有机化学物质的组成和行为理论模型。正如我们将看到的,与我们在算术的出现中所观察到的类似,这些理论模型部分源于对使用这些化学式作为“书面工具”进行符号操作的反思。这种书面工具的作用是编纂知识,从而在更广泛的书面外部表征背景下保存和传递知识的某些方面,使其不只局限于书面语言。
贝采利乌斯引入了化学式,如代表水的H
2
O,它们可以同时表示无机化学领域的系统化基本实验知识,以及有机化学物质的组成和行为理论模型。正如我们将看到的,与我们在算术的出现中所观察到的类似,这些理论模型部分源于对使用这些化学式作为“书面工具”进行符号操作的反思。这种书面工具的作用是编纂知识,从而在更广泛的书面外部表征背景下保存和传递知识的某些方面,使其不只局限于书面语言。
当时研究的一个核心问题是贝采利乌斯所说的“化学比例定律”。
 基于约瑟夫—路易·普鲁斯特(Joseph-Louis Proust,1754—1826)和约翰·道尔顿(John Dalton,1766—1844)的早期工作,
基于约瑟夫—路易·普鲁斯特(Joseph-Louis Proust,1754—1826)和约翰·道尔顿(John Dalton,1766—1844)的早期工作,
 显然,无机化合物中的元素总是以相同的比例存在,而且如果两种元素可以形成不止一种化合物,那么一种元素与固定质量的另一种元素结合后,其质量比总是较小的整数比。尽管这些见解促进了化学原子论的发展,但仍然很难将在无机化学领域获得的经验性见解与有机化学中以及当时的物理学中关于原子本质的思想联系起来。后来,花费了一个多世纪的时间,科学家们才在现代量子理论中找到使化学原子论和物理原子论相协调的可靠基础。在此期间,化学知识的进一步发展是由与化学实验的实际情况更紧密相关的符号系统所塑造的,如贝采利乌斯的化学式。
显然,无机化合物中的元素总是以相同的比例存在,而且如果两种元素可以形成不止一种化合物,那么一种元素与固定质量的另一种元素结合后,其质量比总是较小的整数比。尽管这些见解促进了化学原子论的发展,但仍然很难将在无机化学领域获得的经验性见解与有机化学中以及当时的物理学中关于原子本质的思想联系起来。后来,花费了一个多世纪的时间,科学家们才在现代量子理论中找到使化学原子论和物理原子论相协调的可靠基础。在此期间,化学知识的进一步发展是由与化学实验的实际情况更紧密相关的符号系统所塑造的,如贝采利乌斯的化学式。
化学比例理论中的关键实体实际上并不是原子,而是化学物质中与尺度无关的成分比例。
 化学物质被研究的内容是它们的化学性质和行为,与其机械性质如形状、方向或大小无关。因此,在数量上,重要的是这些物质中与尺度无关的成分比例,这正是贝采利乌斯的化学式所代表的含义。这种表征同时塑造了这种成分比的含义并使之稳定下来,因此有助于向有机化学扩展,而无涉于同时代的原子论概念。
化学物质被研究的内容是它们的化学性质和行为,与其机械性质如形状、方向或大小无关。因此,在数量上,重要的是这些物质中与尺度无关的成分比例,这正是贝采利乌斯的化学式所代表的含义。这种表征同时塑造了这种成分比的含义并使之稳定下来,因此有助于向有机化学扩展,而无涉于同时代的原子论概念。
虽然这些化学式被用作某些化学操作的一阶外部表征,涉及离散的、与尺度无关的成分比例,但它们也是反思用日常语言以及道尔顿的原子和分子来代表化学成分的有限性带来的结果。而且,它们被嵌入一个更广泛的语义网络中,该网络包括化学元素和化合物的概念,以及这些成分元素之间的可测量关系。它们被用于有机化学,并在建立有机化学构成和反应的心智模型方面发挥了建设性作用。化学式成为发达的符号系统的一部分,并服务于建构理论的更复杂目的。现在可以使用化学式进行符号转换,这些符号转换不再代表真实的行动,而是代表可以引发预测的行动和结构模型。在这个例子中,化学式既充当语义关系的符号,又充当图示(icons)。实际上,贝采利乌斯化学式的图示性质——例如,可能会将代表化学元素的字母用加号连接——以镜像形式反映了所表征的心智模型的某些方面,比如,化合物是由一些更基本的成分搭建起来的。
将图表作为书面工具可以确保连续性与创新性,一个引人注目的例子来自借助图表表示质性变化的中世纪传统。近代早期科学对这一传统进行了复兴和探索,为借助无穷小量微积分学理解经典物理学中的运动及运动的概念化奠定了基础。

该方法可以追溯到14世纪的学者尼古拉·奥里斯姆(Nicolas Oresme,1323—1382),他介绍了用图形方式表示有关质的数量变化的学术思想。
 质可以是感觉上的,如白、热或运动,也可以是道德上的,如美德或上帝的恩典。这些质可能会在一定的时间间隔或空间间隔内发生变化。一个例子是热量沿铁棒长度发生变化。另一个例子是速度随时间变化的运动。空间和时间都被认为是质的广延(extension)。在铁棒的例子中,广延是其长度。在运动速度随时间变化的例子中,广延则是时间。
质可以是感觉上的,如白、热或运动,也可以是道德上的,如美德或上帝的恩典。这些质可能会在一定的时间间隔或空间间隔内发生变化。一个例子是热量沿铁棒长度发生变化。另一个例子是速度随时间变化的运动。空间和时间都被认为是质的广延(extension)。在铁棒的例子中,广延是其长度。在运动速度随时间变化的例子中,广延则是时间。
不断变化的质的强度由直线表示,这些直线在其广延的每个点上都是正交垂直的。垂直线的长度代表质在其广延上的“程度”(degree),这是此传统的共同特征。连接所有强度线的上端点将获得一条顶点线。把广延线、顶点线,以及变化的质的第一个和最后一个程度连起来看,我们就得到了一个表示变化的二维图形。其面积代表“质的量”。该图形现在可用于描述质的变化。例如,对于一定时间间隔内的匀速运动,人们获得的是代表“均匀的质”的矩形。三角形则代表“均匀变化的质”,其强度在其广延范围内均匀变化。

在中世纪的背景下,这种图形表征是关于变化的复杂哲学论述的一部分。使用它的目的是分析诡辩、澄清神学问题或讨论一些虚构的情况——比如当苏格拉底不断加快自己的步伐时会发生什么。该方法的图形方面与现代表征形式中借助二维坐标图表示积分有些相似。比如说,考虑将速度作为时间函数描述的运动。在一定的时间间隔内保持匀速运动的例子中,此函数随时间的积分将给出给定时间间隔内,此运动所经过的距离。该积分由矩形的面积表示,而面积由时间间隔和代表匀速的水平线决定。从中世纪的角度来看,我们得到了一种均匀的质。在匀加速运动的例子中,从时间零点的静止状态开始,速度函数将由穿过原点的直线给出;相应的面将是三角形。从中世纪角度来看,我们得到的是均匀变化的质。
但是,从概念上讲,中世纪方法与现代微积分或经典力学非常不同。它既不涉及函数概念也不涉及积分概念,而中世纪的广延、强度和质的程度等概念也与现代框架无关。然而,在近代早期,伽利略、笛卡尔、以撒·贝克曼(Isaac Beeckman,1588—1637)或托马斯·哈里奥特(Thomas Harriot,1560—1621)等前经典科学的主要人物都依靠这种表征质的中世纪传统来解决同样的挑战性问题,这些问题在后来的经典力学中被归给了微积分。
 落体定律的推导就是其中一个例子,即从匀加速的假设出发,下落物体所经过的距离随时间的增加而呈二次方增长。该如何解释运动的现代概念(涉及瞬时速度和平均速度等其他概念)的出现,而中世纪传统对于其出现的作用又是什么呢?
落体定律的推导就是其中一个例子,即从匀加速的假设出发,下落物体所经过的距离随时间的增加而呈二次方增长。该如何解释运动的现代概念(涉及瞬时速度和平均速度等其他概念)的出现,而中世纪传统对于其出现的作用又是什么呢?
答案是由前面讨论过的原理提供的,即外部表征作为思维工具,具有比最初引入时更广阔的适用范围。近代早期的科学家们重新利用了已有的外部表征,以应对新环境下出现的挑战。如前一章所述,这种情况的特点是,越来越多的实践知识和理论知识纠缠在一起,为处理诸如抛体运动、摆的运动或机械效果等当时技术的挑战性对象而被调动起来。在此,我们遇到了中世纪的外部表征,它们充当了从一种概念体系通往另一种概念体系的通道,而它们自身在此过程中也得到了重新解释。
通过近代早期科学倡导者们的新应用,中世纪时期对变化的概念化确实为经典力学和现代微积分的出现奠定了基础。这两个概念体系之间连续性的要素之一是中世纪图表的图示性质。用查尔斯·桑德斯·皮尔士的话来说,图表“在构成其对象的过程中,主要是一种对于关系形式的图示,很容易看出它对于表征必要推论的适当性”。
 比如说,表示匀加速运动的图表无论嵌入何种概念环境,都能通过其几何安排,准确把握这种运动的基本特征。由于我之前提到过的外部表征的生成性歧义,此类图表在近代早期的扩展应用,在新背景和新目的下,促进了新概念关系的出现。
比如说,表示匀加速运动的图表无论嵌入何种概念环境,都能通过其几何安排,准确把握这种运动的基本特征。由于我之前提到过的外部表征的生成性歧义,此类图表在近代早期的扩展应用,在新背景和新目的下,促进了新概念关系的出现。
对运动的研究确实是近代早期科学的中心,在实际实验和思想实验中,人们都考虑了不同的安排。例如,可以将一个加速的下落运动向水平方向偏转,使其转化为匀速运动,这样运动就可以沿着水平面继续下去。该水平运动将继续以一个恒定的速度进行,这个速度在中世纪框架中被称为加速运动的“最终程度”。这样,模糊的中世纪概念“程度”,就可以通过匀速运动中明确定义的恒定速度来解释。于是,它得到了一个直接的操作性含义,类似于经典物理学的瞬时速度,可以用来描述在无限短时间内的运动的特征。
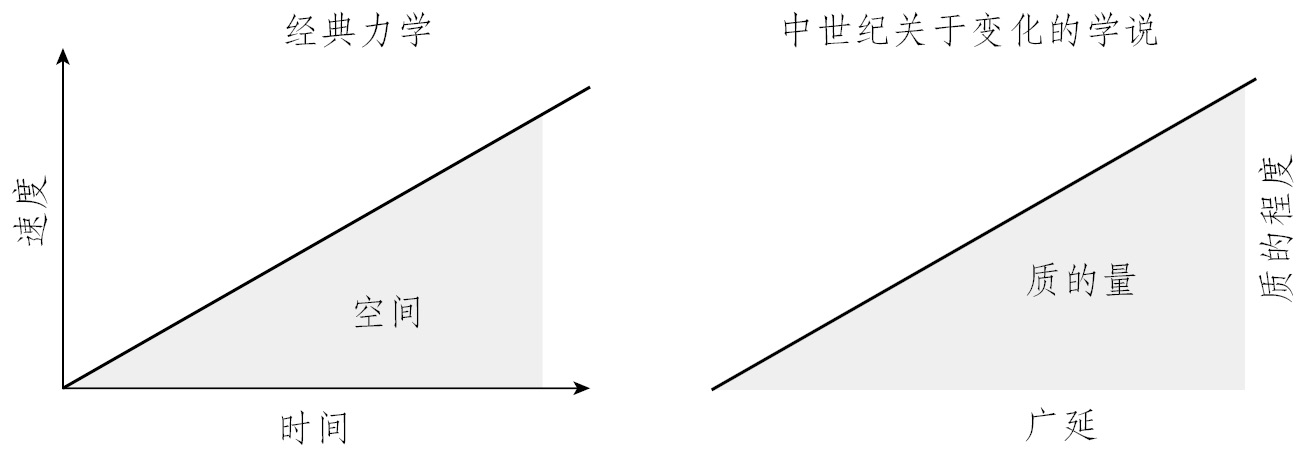
图5.3 变化的不同表征方式。在经典力学中 (左图) ,速度在匀加速落体运动中的增加,可以通过将速度表示为时间线性函数的坐标图表示,并以经过空间的面积作为该函数的积分。在中世纪关于变化的质的学说中 (右图) ,速度可以通过其广延(时间)及其变化程度来表示为“均匀变化形状”或“三角形”的质。尽管这两种概念化大不相同,但图表相似,因此图形表征可以充当它们之间的桥梁。马普科学史研究所图书馆提供
这只是当时所进行的更丰富探索中的一个例子而已,在这些探索中,已有外部表征方式的各种解释都得到了研究,或者被验证,或者被排除。在这一探索过程中,中世纪框架被新经验所丰富,经过扩展、修改,最终被重新解释,并被转化为无穷小微积分以及经典物理学处理运动所需的概念环境的一部分。
这一插曲属于力学知识的长期历史,对其进行研究有助于确定前述知识系统发展过程的许多普遍特征。因此,接下来,我将用这段历史和一些具体示例来阐释其中的一些特征。
[1] Plato (1997b, 1142–1143) [ Republic 7, 525b–526c].(中译引自[古希腊]柏拉图:《理想国》,第291—293页。——译注)