




尽管需求预测本身困难重重,但管理人员仍需在正确的供应链管理中很好地利用预测。目前有许多不同的预测工具和方法,大体可以分为以下四大类:
(1)涉及专家意见收集的判断方法。
(2)涉及消费者行为的市场研究方法。
(3)通过过去的结果预测未来结果的数学方法,即时间序列方法。
(4)基于大量系统变量进行计算的数学方法,即因果方法。
值得提出的是,在对需求进行预测之前,供应链管理者应该做好充分的“课前准备”,对可能影响市场需求的因素进行广泛的收集。
以下这些影响因素应该被充分收集:
(1)宏观经济数据。
(2)市场需求风向。
(3)所涉及的未来时间跨度。
(4)可获得的历史需求数据。
(5)竞争者的当前和未来动向。
(6)可供支持预测的市场调研或试验资金。
当影响未来需求的因素都被考虑之后,接下来就是选择合适的需求预测方法。
定性预测法也称经验判断法,主要是利用市场调查得到的各种信息,根据预测者个人的知识、经验和主观判断,对市场的未来发展趋势做出估计和判断。这种方法的优点是时间短,费用省,简单易行,能综合多种因素;缺点是主观随意性较大,预测结果不够准确,尤其是缺乏对需求变化的精确描述。当企业对预测对象的数据资料掌握不充分或缺乏历史数据(如新产品开发之前的需求预测)、预测影响因素复杂且难于进行定量预测时,这种方法可以优先采用。定性预测法主要包括专家预测法、部门主管讨论法、销售人员意见法等方法。
专家预测法,就是运用专家的知识和经验,考虑预测对象的社会环境,直接分析研究和寻求其特征规律,并推测需求的一种预测方法,又称专家调查法。
这一方法认为通过沟通和公开地分享信息,专家们能够达成一个较好的预测。这些专家可以是外来的专家,也可以是企业内部各职能领域的专家。专家预测法主要包括专家会议法和德尔菲法两种方法。
1.专家会议法
在进行需求预测时,为了达成多数人的一致,可以考虑使用专家座谈。专家会议法,也称专家座谈法,是指由有较丰富知识和经验的人员组成专家小组对预测对象进行座谈讨论,互相启发、集思广益,最终形成需求预测结果的方法。
采用专家会议法进行需求预测应注意三个问题:首先,选择的专家要合适,即专家应该具有代表性,人数要适当;其次,预测的组织工作要合理,会议组织者最好是需求预测方面的专家,应该提前向与会专家提供有关的资料和调查提纲,精心挑选会议主持人,使每一位专家都能够充分发表意见;最后,要注意记录和整理各位专家的意见,进行科学的归纳和总结,进而得出科学的结论。
A公司采用专家会议法,请3位部门经理对下个月的产品需求量进行预测,其结果如表3-1所示。
表3-1 A公司产品需求量预测值
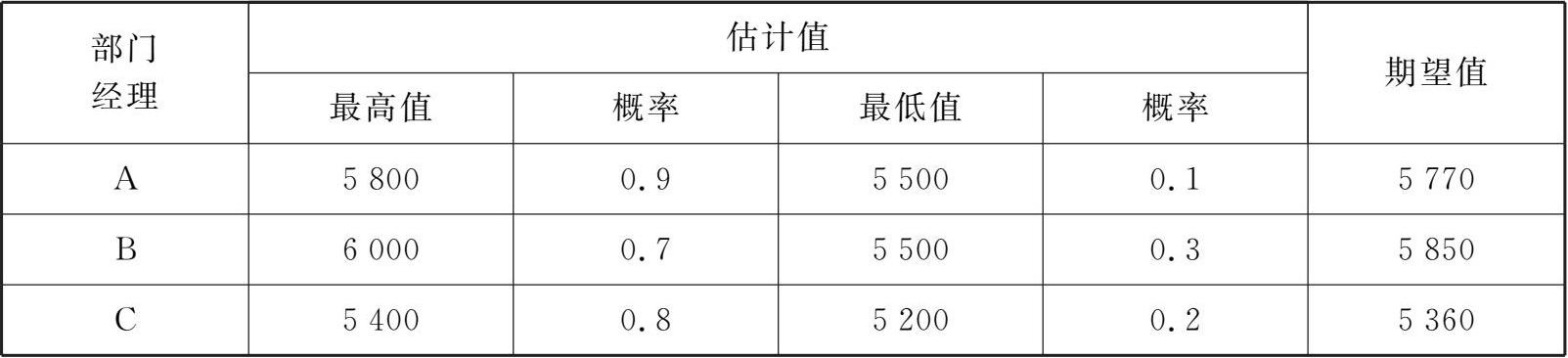
考虑3位部门经理在企业的地位、作用、工作经验和权威性的不同,在实际预测时可以酌情赋予不同权重,比如A经理赋权1.5,B和C经理赋权都为1,此时
综合预测值=
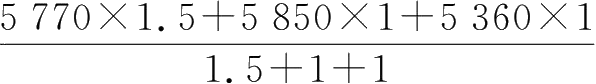 =5 676(元)
=5 676(元)
2.德尔菲法
德尔菲法是另一种专家预测法,它是一种结构化技术,能使一组专家达成一致,却不需要召集这些专家到一起。这种方法可以避免专家组中个别有很强影响力的人主导整个决策过程(专家会议法中常见)。在德尔菲法中,对专家组的每个成员进行书面形式的意见调查。调查结果被汇总并整理,然后每个成员在看到整理后的调查结果后可以调整自己的意见。这个过程通过反复进行几次,最终达成一致。德尔菲法主要有三个特点:匿名性、反馈性与收敛性。
实施德尔菲法一般包括以下五个步骤:
(1)成立预测课题组,确定预测目标;
(2)选择和邀请专家;
(3)设计意见征询表;
(4)逐轮咨询和信息反馈;
(5)采用统计分析方法对预测结果进行定量评价。
美国著名的兰德咨询公司在20世纪50年代接受美国空军委托的课题“如果苏联对美国发动核袭击,其袭击目标会在什么地点及后果如何?”(因为是军方的绝密课题,故以古希腊阿波罗圣殿所在地“德尔菲”来命名)时,发现通过建立数学模型进行定量预测,很难准确地预测出结果,于是决定改为专家估计(背靠背)的方法,依靠其独创的行为集结法成功地综合了众多专家的智慧和直觉判断。从此以后,该方法就被冠以“德尔菲法”而广泛应用于复杂问题的预测与决策中。
这种方法是将企业中与需求预测有关的各级主管(如营销部经理、市场部经理等)召集起来,让他们对未来需求及其变化趋势或特定目标市场的需求进行预测。在此基础之上,将各级主管预测的意见汇总、研究、分析处理,得出最终预测结果。
由于销售人员、经销商更接近市场,他们通常对预期的销售有更准确的感觉。销售人员意见法就是把每个销售人员根据合理的方法做出的销售预期综合在一起。
B公司采用销售人员意见法来预测市场需求。具体做法是先让每个销售员对某产品下一年度的最高销量、最可能销量、最低销量及其概率P分别进行预测,并提出书面意见,再由预测管理部门取其算术平均值作为最终需求预测值。B公司的需求预测计算过程如表3-2所示。
表3-2 B公司的需求预测计算表
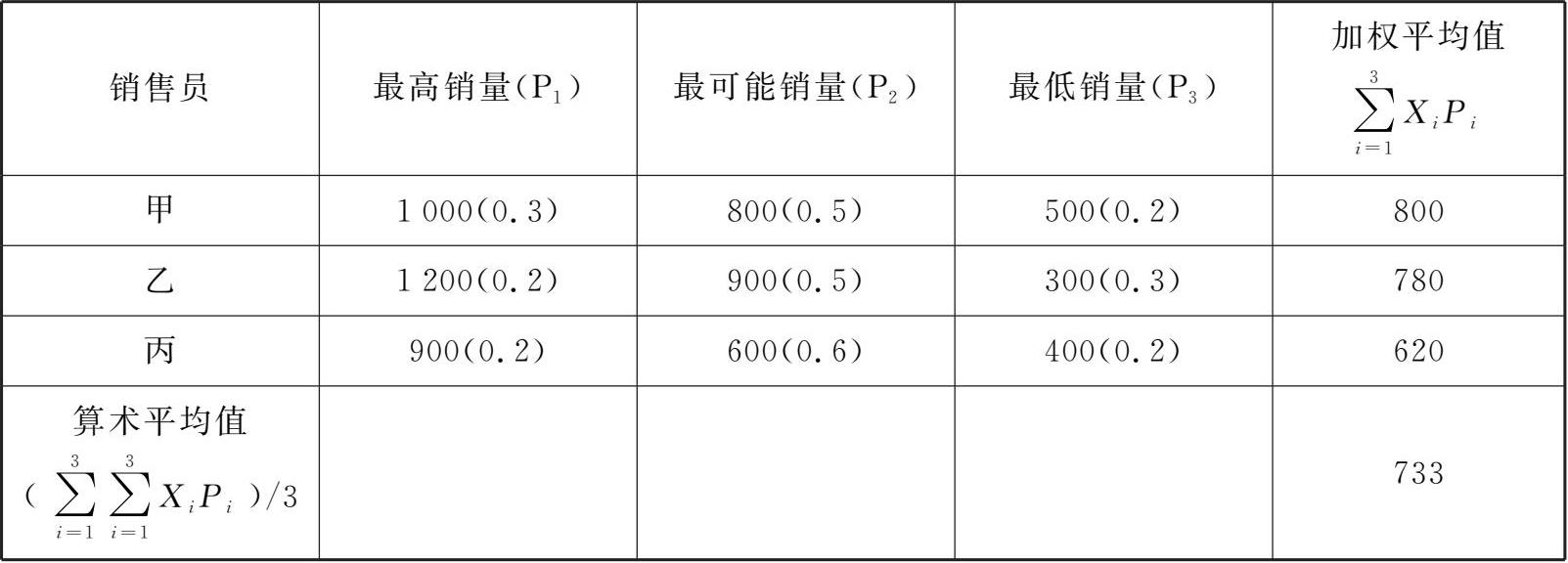
该方法简单明了,易于操作。由于预测值来源于市场第一线的销售人员,可靠性比较大,能较真实地反映公司下一年度的产品需求。实践证明,采用销售人员意见法进行需求预测一般是比较可靠的。尽管销售人员的预测值存在偏差,但通过取其算术平均值后,预测偏差可以在一定程度上相互抵消,结果仍然比较理想。如果能够预先识别并纠正某些预测偏差,则需求预测的准确性将进一步得到提高。
定量预测法是根据以往比较完整的历史统计资料,运用各种数学模型对统计数据进行科学的分析、处理,找出预测目标与有关变量之间的规律性,用于预测未来需求的一种预测方法。其主要特点是需要充分利用统计资料并建立数学模型来进行需求预测。定量预测法着重于对未来需求的量化分析、描述和判断,更多地依据历史统计资料来预测需求,较少受预测者主观因素的影响,因此预测结果相对比较客观。定量预测法主要包括时间序列分析法和因果关系分析法。
时间序列法使用大量过去的数据以估计未来的需求。当需求模式不变、市场条件稳定、历史数据真实可靠时,运用时间序列法预测需求比较有效。常用的时间序列法有许多种,每种方法都有不同的优点和缺点。
1.移动平均法
每个需求预测值是在此之前一定数量实际需求的平均值。这种方法的关键是选择多少个需求点进行处理,从而最小化不规则效应。
例题 3 . 1 某商场2012—2022年的年销售额如表3-3所示,试用移动平均法预测2023年该商场的年销售额。(假设移动时期数为5年)
表3-3 商场年销售额的移动平均计算表
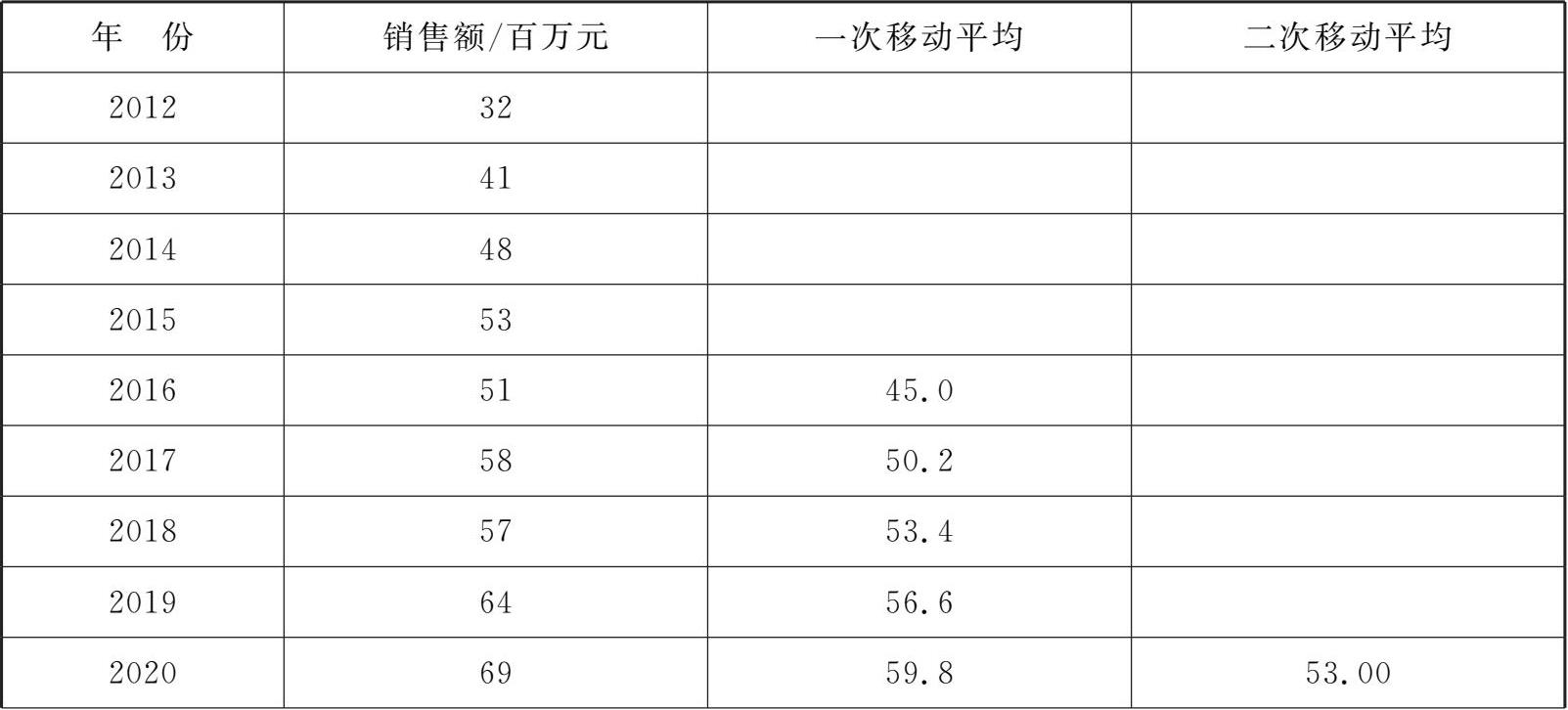
续表

2.加权移动平均法
移动平均法对历史数据赋予相同的权重,但实际情况却是,历史各期物流需求的数据信息对预测未来期需求量的作用是不一样的。越是近期的数据,对预测的参考价值越高,权重应该更大,而对于那些存在季节性变化的需求来说,季节性数据的权重也应该给的高一些。由于加权移动平均法能区别对待历史数据,通常能够更为贴近实际地利用历史数据进行需求预测。经验法和试算法是选择权重的最简单方法。
加权移动平均法的计算公式如下:
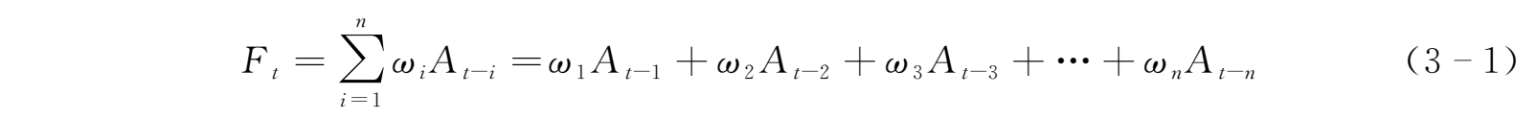
式中, F t ——当期的需求预测值;
A t - i ——第 i 期的需求观测值;
ω i ——第 i 期数据的权重;
ω 1 + ω 2 + …+ ω n = 1;
n ——预测的时期数。
例题 3 . 2 一家超市经理发现,在过去四个月的时间内,某商品的最佳预测结果由当月该商品实际销量的40%、倒数第二个月销量的30%、倒数第三个月销量的20%和倒数第四个月销量的10%组成。这四个月(由远到近)的销量分别是100件、90件、105件和95件。试预测第五个月的需求预测值。
解
:
F
5
=
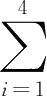 ω
i
A
t-i
=
0.4
×
95
+
0.3
×
105
+
0.2
×
90
+
0.1
×
100≈98(件)
ω
i
A
t-i
=
0.4
×
95
+
0.3
×
105
+
0.2
×
90
+
0.1
×
100≈98(件)
3.指数平滑法
(1)简单指数平滑法。
移动平均法下需要大量连续的历史数据才能进行需求预测。有时,我们仅仅只能根据上一期的历史数据预测当期的需求,此时,可以采用指数平滑法来进行预测,其每个预测值是前一预测值和前一实际需求的加权平均。因此,该方法和移动平均较为类似,不同之处在于其需要对过去的数据乘以权重,越是近期的数据权重越大。该方法无须大量连续历史数据,模型简单,计算过程简单,预测的准确度比较高,但其预测的误差有传递性。
计算公式如下:
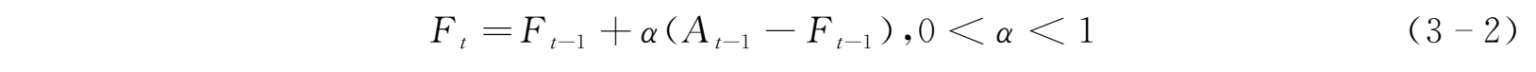
式中, F t ——当期的需求预测值;
F t-1 ——上一期的需求预测值;
A t-1 ——上一期的需求观察值;
α ——平滑系数。
例题 3 . 3 某产品的长期需求比较稳定,平滑系数 α= 0.05,假设上个月的预测值为2 050件,上个月的实际需求量为2 000件。试预测本月的需求量。
解 : F t =F t-1 +α ( A t -1- F t -1) = 2 050 + 0.05 × (2 000-2 050)≈2 048(件)
即本月该产品的需求预测值为2 048件。
指数平滑法的关键一步是要选择合理的平滑系数 α 。 α 将直接影响过去各期观察值的作用。当 α 取值较大时,对时间序列的修匀程度较小,平滑后的序列能够反映原序列的变化情况,适用于变化较大的时间序列。当 α 取值较小时,对时间序列的修匀程度较大,平滑后的序列对原序列的变化反应较迟钝,适用于变化较小,较平滑的时间序列。在实际预测过程中, α 值需要经过比较才能确定。从理论上来讲, α 值取0~1的任意值都可以,其原则是保证预测的误差最小。根据经验,一般可以选择不同的 α 值进行试算,然后分别计算其均方差MSE,选择MSE最小的 α 值。
误差的均方差计算公式为:
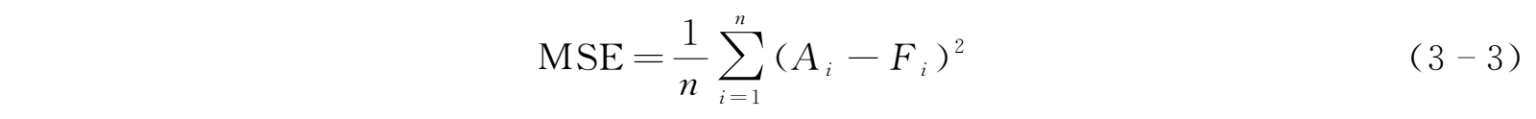
式中, F i —— i 期的需求预测值;
A i —— i 期的需求观察值;
n ——期数。
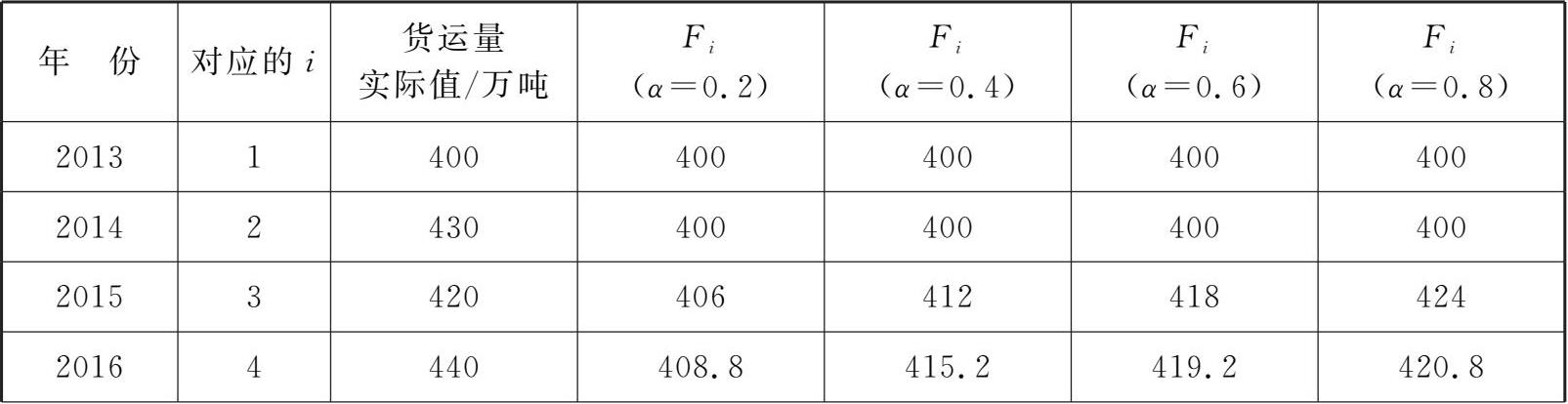
例题 3 . 4 某地区进行物流规划,需要预测未来的货运量数据,统计收集到的2013—2022年的历史数据如表3.4所示。试利用指数平滑法预测其2023年的货运量数据。
解 :由表3-4数据可知,当 α= 0.2时, F 2 =F 1 =A 1 = 400,则 F 3 =F 2 +α ( A 2 - F 2 ) = 400 + 0.2 × (430-400) = 406; F 4 = F 3 +α ( A 3 - F 3 ) = 406 + 0.2 × (420-406) = 408.8。
以此类推,我们可以得到 α= 0.2, α= 0.4, α= 0.6, α= 0.8时的预测试算值(详见表3-4)。
表3-4 不同 α 值下的预测试算值
续表
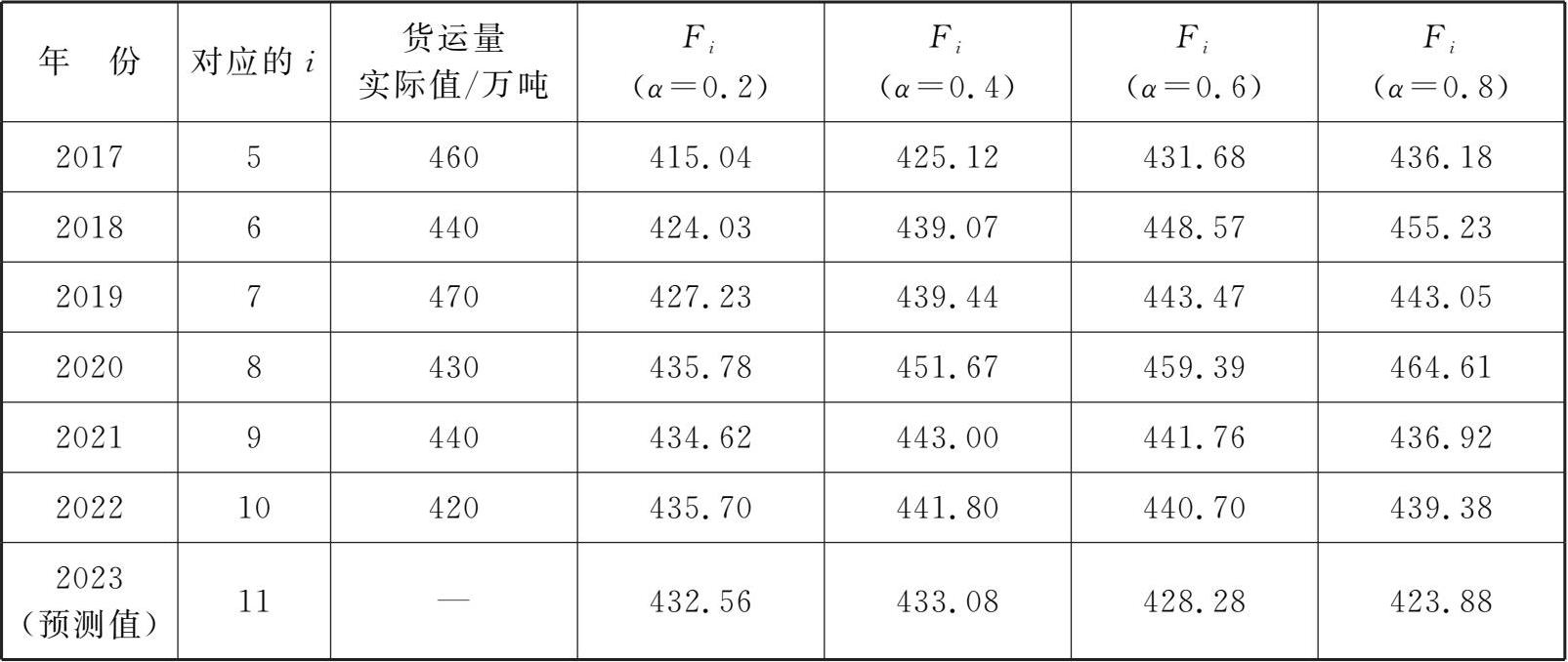
从试算结果中可以看出,不同 α 值下的2023年的预测值存在一定的差异,我们可以利用误差均方差MSE计算方法来选择合理的 α 值,选择过程如表3-5所示。
表3-5 不同 α 值下的MSE值
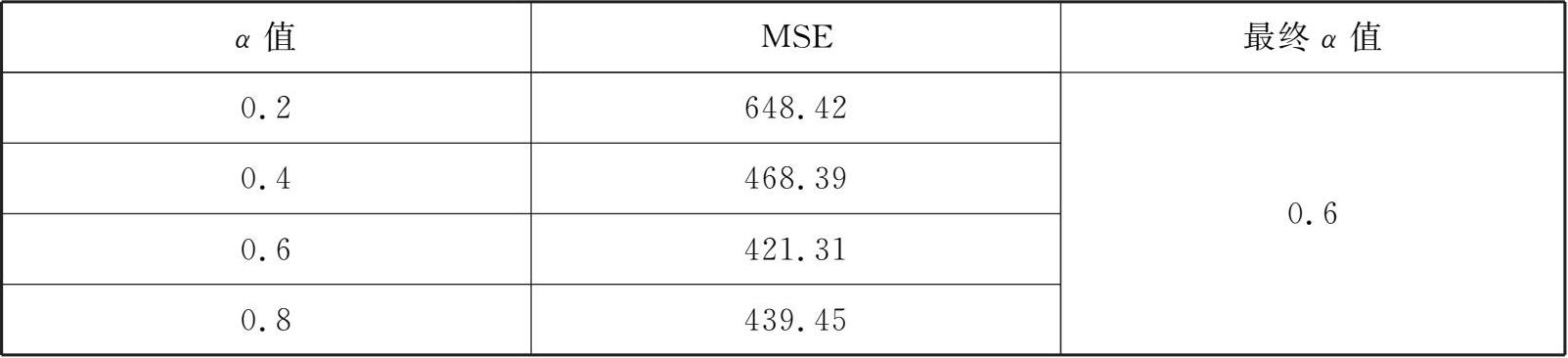
因此,2023年的预测值最终选择428.28万吨。
(2)Holt's模型(趋势调整的指数平滑法)。
在需求系统成分中仅包括需求水平和需求趋势,而没有季节系数的情况下,使用Holt's模型(趋势调整的指数平滑法)最合适。这种情况下:
需求的系统成分=需求水平+需求趋势
Holt's模型由Holt于1957年提出。它与一般的指数平滑模型不同的是它对趋势数据直接进行平滑,并对时间序列进行预测,需要考虑的是两个平滑参数以及初值的选取问题,也被称为Holt双参数线性指数平滑模型。利用该模型预测,需要两个基本平滑公式和一个预测公式。两个平滑公式分别对时间数列的两种因素进行,它们是:
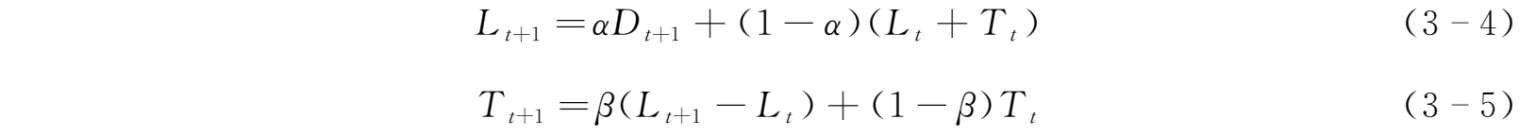
以及一个预测公式:
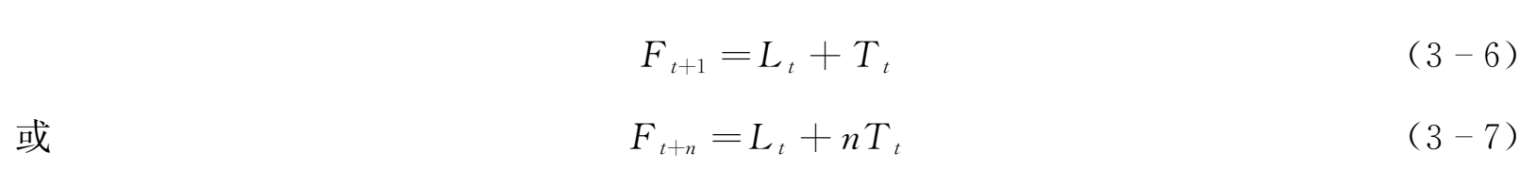
式中, α 为需求水平的平滑指数,0< α <1; β 为需求趋势的平滑指数0< β <1; D t 代表 t 期实际观察值; F t+1 代表预测值; L t 代表平均需求水平; T t 代表需求增长趋势。我们可以观察到,不管是需求水平修正还是需求趋势修正,修正后的预测值(需求水平或需求趋势)都是实际观测值和以前预测值的加权平均。
例题 3 . 5 一家手机制造商观察到过去6个月中,它的最新款手机的需求一直保持增长,观测到的实际需求值(单位为百个)分别为 D 1 = 8 415, D 2 = 8 732, D 3 = 9 014, D 4 = 9 808, D 5 = 10 413和 D 6 = 11 961,请用趋势调整的指数平滑法预测其第7期的需求量。其中α = 0.1,β = 0.2。
解 :我们可以运用线性回归法求出需求水平和需求趋势的初始预测值。首先,我们对需求和时间进行线性回归(利用Excel的数据工具|数据分析|回归),根据手机的实际销售数据可得: L 0 = 7 367和 T 0 = 673。
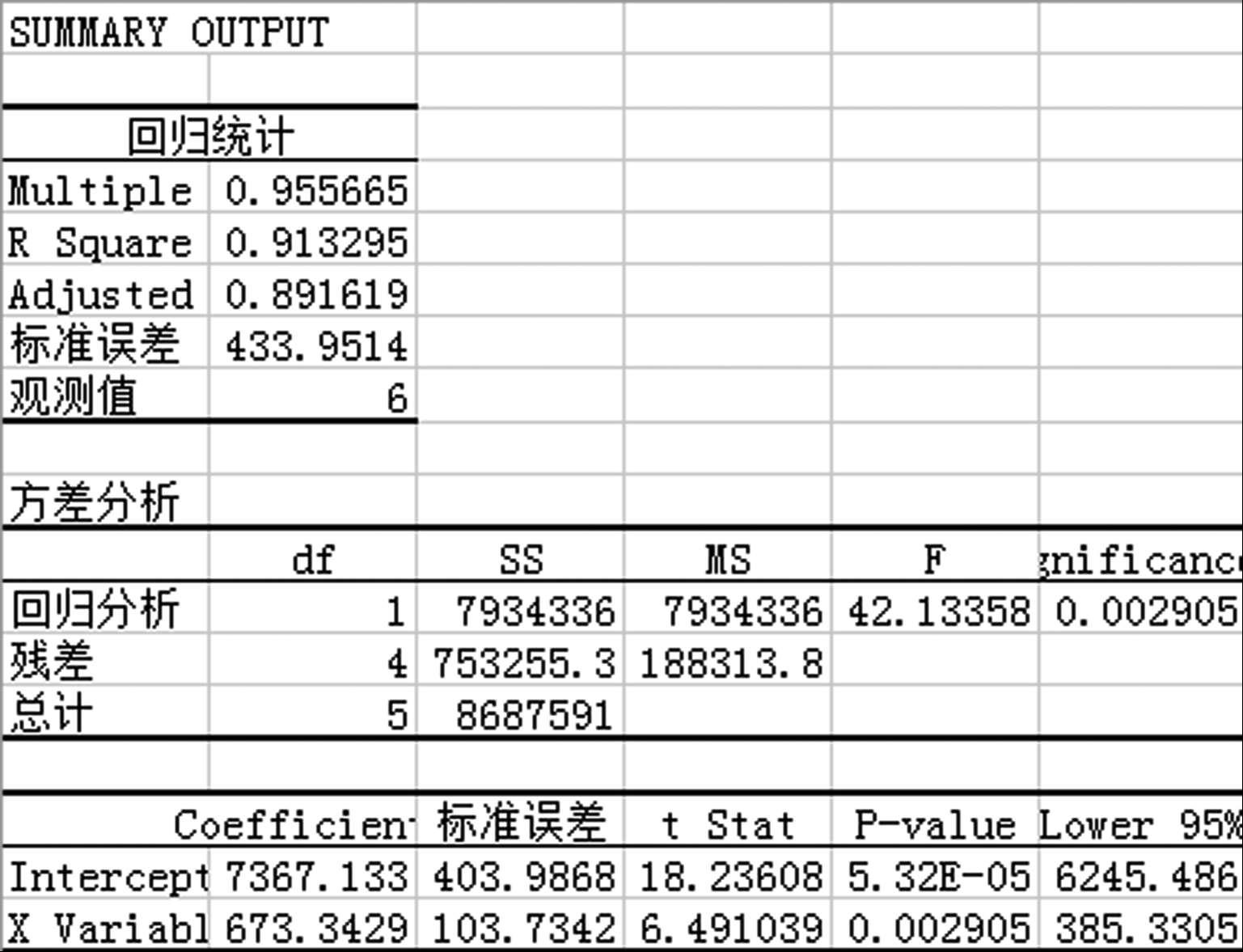
由公式可知第1期的预测值为:
F 1 = L 0 + T 0 =7 367+673=8 040
第1期的需求实际观测值为 D 1 = 8 415,那么第一期的预测误差如下:
E 1 = F 1 - D 1 =8 040-8 415=-375
当 α =0.1, β =0.2时,利用基本平滑公式,可对第1期需求水平和需求趋势的预测值进行修正,得到:
L 1 = αD 1 + (1- α )( L 0 + T 0 )=0.1×8 415+0.9×8 040=8 078
T 1 = β ( L 1 - L 0 )+ (1- β ) T 0 =0.2× (8 078-7 367)+0.8×673=681
由于第1期需求的初始预测值过低,所以,修正过程中把第1期的需求水平预测值从8 040提高到8 078,需求趋势预测值从673提高到681,于是我们可以继续求得第2期的预测值:
F 2 = L 1 + T 1 =8 078+681=8 759
同理可得:
L 2 =8 755, T 2 =680, L 3 =9 393, T 3 =672, L 4 =10 039, T 4 =666,
L 5 =10 676, T 5 =661, L 6 =11 399, T 6 =673
从而得到第7期的预测值为:
F 7 = L 6 + T 6 =11 399+673=12 072
(3)Winter模型(趋势和季节调整的指数平滑法)。
当需求的系统成分包括需求水平、需求趋势和季节系数时,Winter模型最为适用。此时:
需求的系统成分 = (需求水平 + 需求趋势) × 季节系数
假定每次季节性循环包含的期数为 p 。首先,我们需要对需求的初始水平( L 0 )、需求的初始趋势( T 0 )和季节系数( S 1 ,…, S p )进行预测。
在第 t 期,事先给定需求水平为 L t 、需求趋势为 T t 和季节系数为 S t ,…, S t + p-1 ,那么未来时期的预测值计算如下:
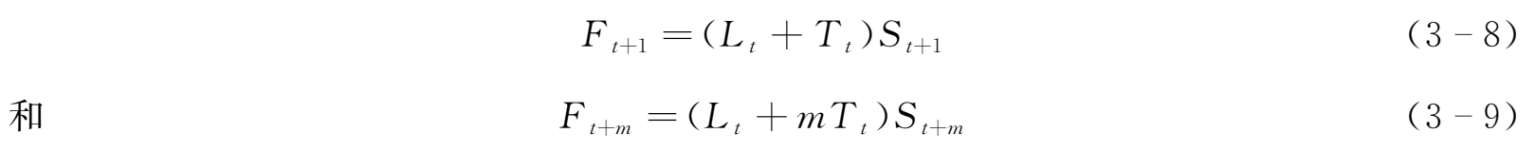
观测到第 t +1期的需求后,我们对需求水平、需求趋势和季节系数的预测值进行修正:
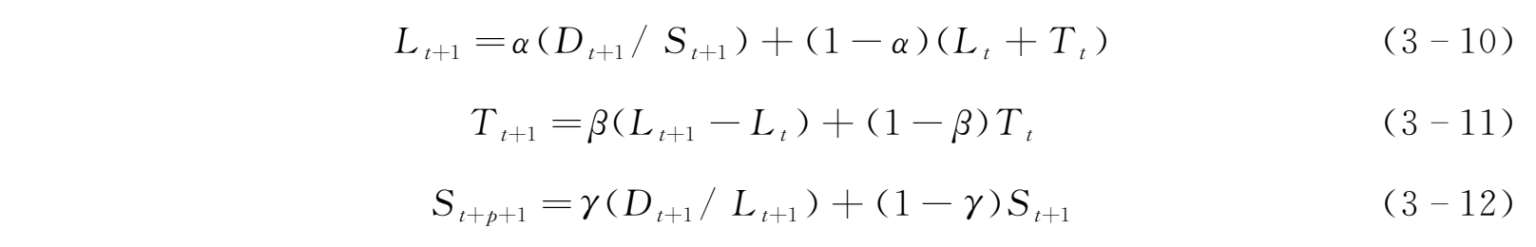
式中, α 为需求水平的平滑指数,0< α <1; β 为需求趋势的平滑指数,0< β <1; γ 为季节系数的平滑指数,0< γ <1; D t 代表 t 期实际观察值; F t+1 代表预测值。从以上公式中,我们可以知道,不管是需求水平修正还是需求趋势修正、季节系数修正,修正后的预测值(需求水平、需求趋势和季节系数)都是实际观测值和以前预测值的加权平均。
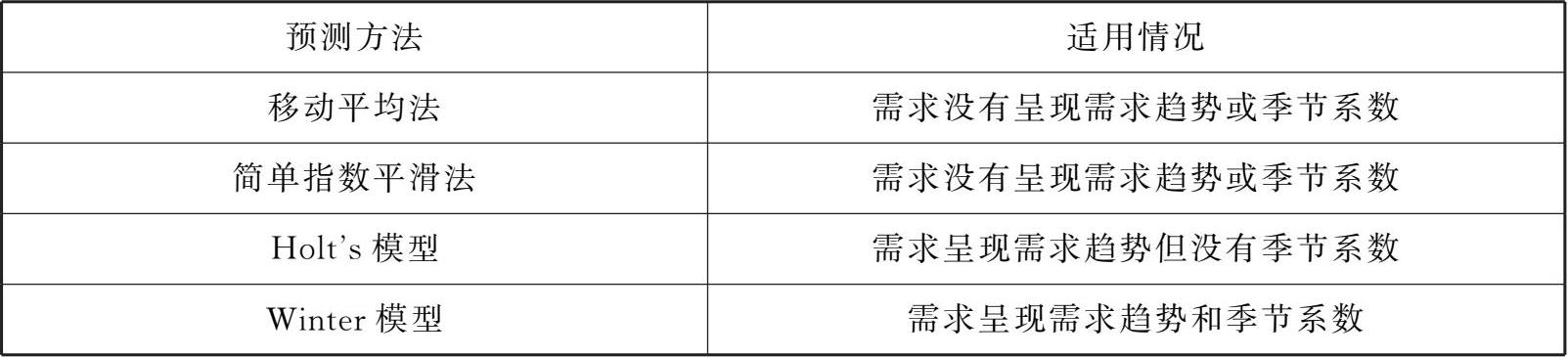
我们将前面讨论的几种预测方法和它们的适用环境进行总结,如表3-6所示。
表3-6 不同预测方法的适用性
因果关系分析法是利用引起需求变化的变量来推测需求变化趋势的一种预测方法。当某种产品(或服务)的需求量与自变量(如价格、消费偏好等)之间存在因果关系时,可以使用因果关系分析法来预测需求。它是利用实际数据而不是预测数据来进行预测的。这些变量包括通货膨胀率、GNP、失业率、天气状况、其他产品的销售情况等。这些变量与需求变化之间或具有确定性关系(或称函数关系),或具有不确定性关系(或称相关关系)。我们可以找出这些因果关系,并据此预测出需求的变化趋势。常见的因果关系分析法包括回归分析法和经济计量法。
1.回归分析法
回归分析法是指在掌握大量观察数据的基础上,利用数理统计方法建立因变量与自变量之间的回归关系函数,通过回归方程来描述因变量与自变量之间数量平均变化关系的预测方法。
回归分析法有多种分类方法。若按照自变量的个数,可将其划分为一元回归分析和多元回归分析。当研究的因果关系只涉及因变量和一个自变量时,称为一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,称为多元回归分析。此外,根据自变量与因变量之间因果关系的函数关系是线性还是非线性,可将其划分为线性回归分析和非线性回归分析。其中,线性回归分析是最基本的回归分析方法,也是一种重要的需求预测方法。
例题 3 . 6 某地区搜集到新房屋销售价格 y 和房屋面积 x 的数据,如表3-7所示。
表3-7 房屋销售价格表

(1)求线性回归方程。
(2)利用(1)的结果预测房屋面积为150平方米时的销售价格。
解 :(1)由已知数据可计算得到:
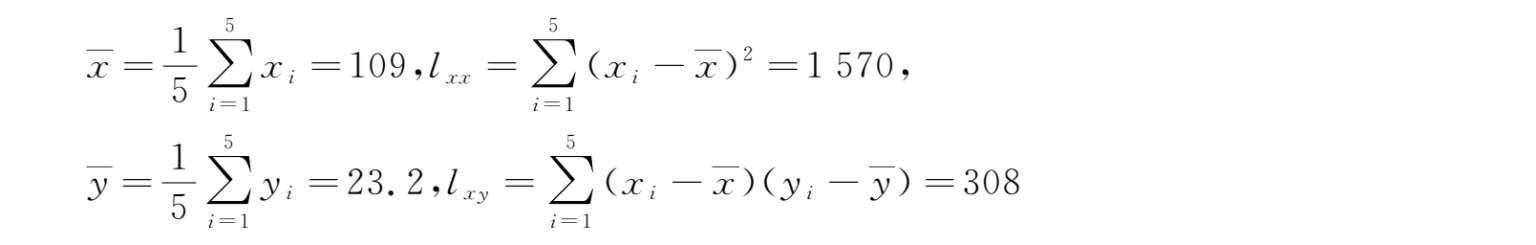
设所求线性回归方程为:
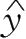 =a+bx
=a+bx
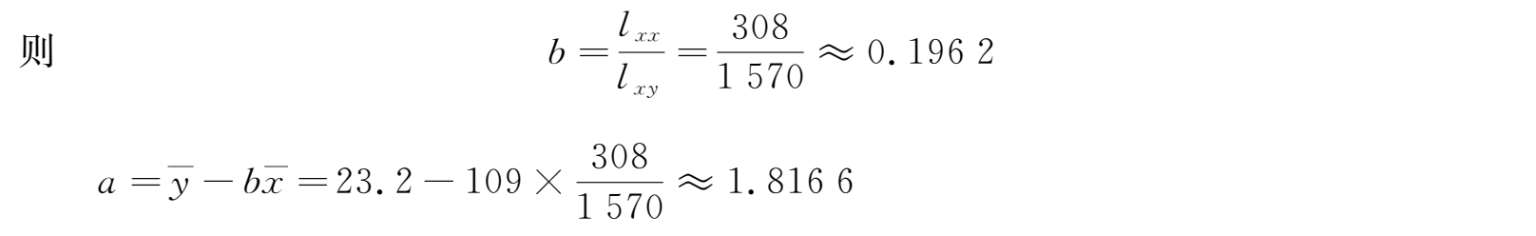
故所求线性回归直线方程为:
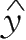 =
0.196 2
x+
1.816 6。
=
0.196 2
x+
1.816 6。
(2)根据(1)的结果,当 x= 150平方米时,销售价格的预测值为:
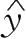 =
0.196 2
×
150
+
1.816 6
=
31.246 6(万元)
=
0.196 2
×
150
+
1.816 6
=
31.246 6(万元)
2.经济计量法
经济计量法是揭示市场变量之间复杂因果关系数量变化的方法。这种方法是以经济理论和事实为依据,在定性分析的基础上,利用数理统计方法建立一组联立方程式,通过经济计量模型来描述预测目标与相关变量之间经济行为结构的动态变化关系的预测方法。
需求预测的方法很多,如何选择,需要结合实际问题的特点和预测技术的能力来决定。下面介绍一些选择的标准:
(1)考虑预测的目的,明确进行预测的目的是想进行大致的预测还是精确的预测。
(2)考虑预测对象的系统动态性,即预测对象的系统对经济数据的变化是否反应灵敏,是否具有季节性或趋势性。
(3)考虑历史数据对预测未来需求的重要程度。如果历史数据很重要,时间序列方法就有意义;如果系统变化太显著而使得过去的数据作用下降,则判断或市场调查方法更有效。
(4)对于处于不同生命周期的产品采用不同的预测方法,其效果可能会更好。对于处于引入期的产品,应该采用市场调查法和判断法;对于成长期的产品,采用时间序列法较好;对于成熟期的产品,最好采用时间预测法和因果法。
最后,结合使用上面介绍的不同方法,预测的质量通常会得到改善,因为在给定的情形下,一般很难直接从几种可用预测方法中挑出最有效的方法。