阅读材料

数学思维方法的启示——极限

极限是现代数学分析奠基的基本概念，函数的连续性、导数、积分以及无穷级数的和等都是用极限来定义的.

直观的极限思想起源很早。公元前5 世纪，希腊数学家安提丰(Antiphon,公元前426年—公元前373年）在研究化圆为方问题时创立了割圆术，即从一个简单的圆内接正多边形(如正方形或正六边形）出发，把每条边所对的圆弧二等分，连接分点，得到一个边数加倍的圆内接正多边形，当重复这一步骤足够多次时，所得圆内接正多边形的面积与圆的面积之差将小于任何给定的限度。实际上，安提丰认为圆内接正多边形与圆最终将会重合。稍后，另一位希腊数学家布里松(Bryson)考虑了用圆的外切正多边形逼近圆的类似步骤。这种以直线形逼近曲边形的过程表明，当时的希腊数学家已经产生了初步的极限思想。公元前4世纪，欧多克索斯(Eudoxus,公元前400年—公元前347年）将上述过程发展为处理面积、体积等问题的一般方法，称为穷竭法.

中国古代成书于春秋末年的《庄子 · 天下篇》中记载了这样一个命题：“一尺之棰，日取其半，万世不竭。”是说一尺长的一根木棒，每天截取其一半，则这个过程一万年也不会完结。成书于春秋末至战国时期的《墨经》对上述过程另有一种观点。《墨经 · 经下》：“非半弗新则不动，说在端.”《墨经 · 经说下》：“非, 半；进前取也，前则中无为半，犹端也；前后取，则端中也. 必半，毋与非半，不可 也。”大意是，对一条有限长的线段进行无限多次截取其半的操作，最终将得到一个不可再分的点，这个点在原8线段上的位置是由截割的方式确定的。公元263年，魏晋间杰出数学家刘徽创立割圆术以推求圆面积和弓形面积，使用极限方法计算了开平方、开立方中的不尽根数以及棱锥的体积.

应该指出,17世纪中叶以前，原始的极限思想与方法曾在世界上一些不同地区和不同时代多次出现，特别是在17世纪早期，一些杰出的数学家从极限观念出发，发展了各种高超的技巧，解决了许多关于求瞬时速度、加速度、切线、极值、复杂的面积与体积等方面的问题。然而，所有这些工作都是直接依赖直观的、不严密的，与今天所说的极限有很大差别.

最早试图明确定义和严格处理极限概念的数学家是牛顿(I.Newton,1643—1727).他在《论曲线的求积》中使用了“初始比和终极比”方法，它实际上就是极限方法。他还指出，用当时流行的，他本人也经常使用的不可分量或无穷小量来进行论证，只不过是以终极比(极限）作为严格数学证明的一种方便的简写法，并不是取代这种严格的证明.

1687年,牛顿的名著《自然哲学的数学原理》出版,书中充满无穷小思想和极限论证,因而有时被看作是牛顿最早发表的微积分论著.在第一节的评注中,牛顿特别说明:“所谓两个垂逝量(即趋于零的量)的终极比,并非指这两个量消逝前或消逝后的比,而是指它们消逝时的比……两个量消逝时的这种终极比,并非真的是两个终极量的比,而是两个量之比在这两个量无限变小时所收敛的极限.这些比无限接近这个极限,与其相差小于任何给定的差别,但绝不在这两个量无限变小以前超过或真的取得这个极限值.”这本书第一编引理Ⅰ实际上是牛顿想给极限下个定义:“两个量或量之比,如果在有限时间内不断趋于相等,且在这一时间终止前互相靠近,使得其差小于任意给定的差别,则最终就成为相等.”用现代记号来写,就是说,若给定 ε >0,而在 t 足够接近 a 时, f ( t )与 g ( t )之差小于 ε ,则

在18世纪，牛顿的上述思想被进一步明确和完善.1735年，英国数学家罗宾斯(B.Robins,1707—1751)写道：“当一个变量能以任意接近程度逼近一个最终的量(虽然永远不能绝对等于它），我们定义这个最终的量为极限.”1750年，法国著名数学家达朗贝尔(J.L.R.D'Alembert,1717—1783)在为法国科学院出版的《百科全书》第四版所写的条目“微分”中指出：“牛顿……从未认为微分学是研究无穷小量，而认为只是求最初比和最终比，即求出这些比的极限的一种方法。”他对极限的描述是：“一个变量趋于一个固定量，趋近程度小于任何给定量，且变量永远达不到固定量.”

虽然到18世纪中叶极限已成了微分学的基本概念，但在19世纪以前，它仍缺乏精确的表达形式。极限概念和理论的真正严格化是由柯西开始，而由魏尔斯特拉斯完成的.

1821年,法国数学家柯西(A.L.Cauchy,1789—1857)在《分析教程第一编 · 代数分析》中写道:“当一个变量相继取的值无限接近于一个固定值,最终与此固定值之差要多小就有多小时,该值就称为所有其他值的极限.”“当同一变量相继取的数值无限减小,以至降到低于任何给定的数,这个变量就成为人们所称的无穷小或无穷小量.这类变量以零为其极限.”“当同一变量相继取的数值越来越增加以至升到高于每个给定的数,如果它是正变量,则称它以正无穷为其极限,记作+∞;如果是负变量,则称它以负无穷为其极限,记作-∞.”柯西没有使用 ε-δ 型的极限,他的以零为极限的变量也不可能适应这个框架.虽然如此,在某些场合他还是给出了一种 ε-δ 式的证明.

1860—1861年,德国数学家魏尔斯特拉斯对极限概念给出了纯粹算术的表述.以往极限概念总是具有连续运动的含义——如果当 x 趋向于 a 时 f ( x )趋向于 L ,则称 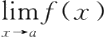= L .魏尔斯特拉斯反对用这种“动态”方式来描述极限概念,而代之以仅仅涉及实数而不依靠运动或几何思想的“静态”描述:

如果对于给定的 ε >0,存在数 δ >0,使得当0<| x - a |< δ 时,| f ( x )- L |< ε 成立，则 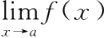= L .

用这种方式把微积分中出现的各种类型的极限重新表述，分析学的算术化即告完成，从而使得微积分明确地达到了20世纪中所阐释的形式. MFOUcICK7JfEKyTn9YUDLgyxFcvkQyGGnMCK030vqnqPpCyYOZcvwl6knHyGV8c1