




1.1节,介绍了合成孔径雷达和逆合成孔径雷达成像方方面面的情况,详细情况将在本书的各章里讨论。雷达成像有别于一般雷达的最主要点是用合成孔径技术(也可用多普勒效应来解释)得到高的横向分辨率。为了使读者在阅读后面的各章时,能集中精力去掌握各种具体情况下的特殊方法,先在这里对雷达成像的基本概念和基本原理进行简单介绍。
为了便于理解,先从介绍逆合成孔径技术开始。
逆合成孔径的一般情况是雷达不动,而目标(如飞机)运动。为简化分析,暂假设雷达和目标位于一个平面,且目标做匀速直线飞行。
可以将目标的运动分解成平动和转动两个分量。设目标上有一个参考点,目标平动是指该参考点沿目标运动轨迹移动,而目标相对于雷达射线的姿态(可用目标轴向与雷达射线的夹角表示)保持不变;转动分量是指目标围绕该参考点转动。不难看出,当目标以散射点模型表示时,若目标处于雷达的远场,雷达电磁波可用平面波表示,在只有平动分量的情况下,目标上各散射点回波的多普勒值完全相同,对雷达成像没有贡献。设法将平动分量补偿掉(如何补偿后面会详细讨论),则相当于把目标上的参考点移到转台轴上,而成为对转台目标成像[图1.4(a)所示]。
转台目标成像的原理是容易理解的。为了成像,必须有高的二维分辨率。在平面波照射下,纵向分辨率主要依靠信号的宽频带(Δ f r ),在对回波作匹配滤波的条件下,纵向分辨率
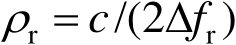
(1.1)
式(1.1)中, c 为光速。
如信号频带
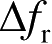 为400MHz,则
ρ
r
为0.375m,考虑到脉压过程中为了降低距离副瓣而做的加权,
ρ
r
会展宽到约为0.5m。
为400MHz,则
ρ
r
为0.375m,考虑到脉压过程中为了降低距离副瓣而做的加权,
ρ
r
会展宽到约为0.5m。
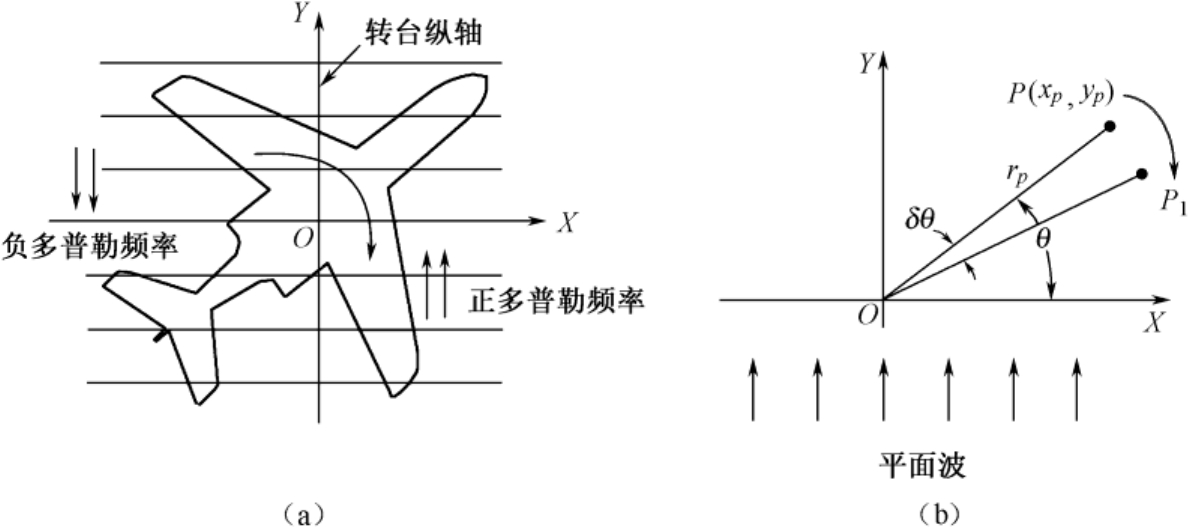
图1.4 转台目标成像的示意图
高的横向分辨率主要靠多普勒效应,如图1.4(a)所示,当目标以顺时针方向转动时,目标上各散射点的多普勒频率是不同的。位于轴线(轴心至雷达的连线)上的散射点没有相对于雷达的径向运动,其子回波的多普勒频率为零,而在其右或左侧的多普勒频率分别为正或负,且离轴线越远,多普勒的值也越大。于是,将各个距离单元的回波序列分别通过傅里叶变换到多普勒域,只要多普勒分辨率足够高,就能将各单元的横向分布表示出来。
如图1.4(b)所示,设在相邻两次观测中目标对于雷达视线转过了一个很小的角度 δ θ ,它上面的某一散射点则从 P 点移到了 P 1 点,其纵向位移为
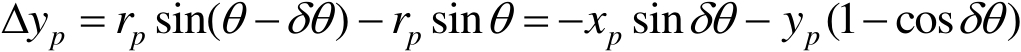
(1.2)
式(1.2)中,
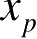 ,
,
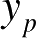 为散射点
P
相对于转台轴心的坐标,且
为散射点
P
相对于转台轴心的坐标,且
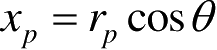 ,
,
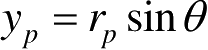 。纵向位移
。纵向位移
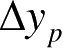 引起子回波的相位变化为
引起子回波的相位变化为
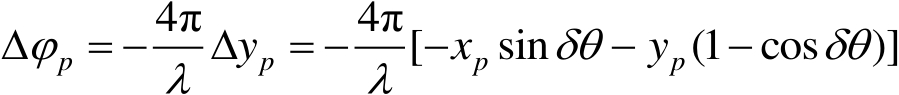
(1.3)
若 δ θ 很小,则式(1.3)可近似写成
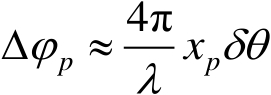
(1.4)
式(1.4)表明,两次回波的相位差正比于横距
x
p
。该散射点相邻两个周期的回波相差一个相位旋转因子
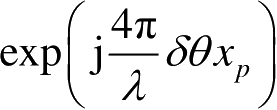 ,当转台连续转动时,子回波的相位变化表现为多普勒频率,
x
p
越大,则该散射点子回波的多普勒频率也越高。
,当转台连续转动时,子回波的相位变化表现为多普勒频率,
x
p
越大,则该散射点子回波的多普勒频率也越高。
目标均匀转动,并在观测过程中接收到 M 次回波,即总转角Δ θ = M δ θ ,当两散射点的横向距离差为Δ x 时,两散射点子回波总的相位差为
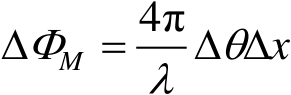
(1.5)
用傅里叶变换做多普勒分析时,只要
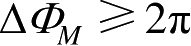 ,两点即可分辨,这时的横距分辨率
ρ
a
为
,两点即可分辨,这时的横距分辨率
ρ
a
为
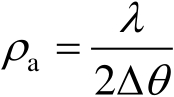
(1.6)
上面是以某瞬间的散射点位置与子回波多普勒频率的关系来说明横向高分辨率的,但是多普勒分辨率越高,所需的相干积累时间就越长,散射点是否会移动而改变位置了呢?移动肯定存在,但在一般情况下影响不大,可以举一个数字例子。若
λ
为3cm,
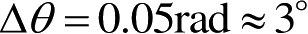 ,则
ρ
a
=0.3 m。可见对于厘米波雷达,为得到零点几米的横向分辨率,所需的总的转角是很小的,一般为3°~5°。
,则
ρ
a
=0.3 m。可见对于厘米波雷达,为得到零点几米的横向分辨率,所需的总的转角是很小的,一般为3°~5°。
虽然很小的转角就能实现转台目标成像,但在转动过程中,散射点还是要有纵向移动的,偏离轴线越远,则移动也越大。设目标横向尺寸为10m,当总转角为0.05rad时,两侧散射点的相对纵向移动为0.5m;若横向尺寸为40m,则相对纵向移动为2m。这已经超过了一般逆合成孔径雷达距离分辨单元的长度,即在此期间产生了越距离单元徙动。
前面提到过,在一般的成像算法中,是按距离单元将许多周期的数据序列做多普勒分析得到高分辨率的,若在此期间产生了越距离单元徙动,则该散射点的子回波序列将分段分布在两个或更多个距离单元里,且在每个距离单元的驻留时间要缩短。
实际上,由于受到系统分辨率的限制,从雷达回波数据重建图像的形状和原物体是有区别的,以理想的点目标为例,重建图像的纵向分布由于信号有一定的频带(Δ f r )而时间展宽为1/Δ f r ,其横向(多普勒)分布由于相干积累时间 T 的限制,而多普勒展宽为1/ T 。还可以在距离-多普勒平面画出上述重建图像的形状,该图像的数学表示式称为点散布函数,信号频带越宽、相干时间越长,则点散布函数就越集中,表明该系统具有越高的分辨率。当散射点产生了越距离单元徙动时,点散布函数会在纵向展宽,同时由于在一个距离单元里的驻留时间缩短,其横向(多普勒向)也会展宽,其结果是使转台目标的重建图像具有不同的点散布函数:离转轴越远,点散布函数就越差。不过,在实际应用中,上述现象通常可以容忍。但也有方法来消除越距离单元徙动产生的不良影响,这将在后面介绍。
上面是将运动目标通过平动补偿成为匀速转动的平面转台目标,当飞机做直线平稳飞行时,一般满足或近似满足上述条件。如果飞机做加速或减速的直线飞行,仍可补偿成平面转台目标,只是转速是非均匀的。更有甚者,如果飞机做变向机动飞行,则平动补偿后的转台目标是三维转动的。这些问题也将在后面讨论。
前面提到,当用飞机平台上的雷达观测固定的地面场景时,可以用多普勒效应来说明其高的横向分辨率,如图1.5(a)所示与飞机航线平行的一条地面线上,在某一时刻,线上各点到雷达天线相位中心连线与运动平台速度向量的夹角是不同的,因而具有不同的瞬时多普勒频率。但是,为了得到高的多普勒分辨率,必须有长的相干积累时间,也就是说飞机要飞一段距离,它对某一点目标的视角是不断变化的。图1.5(b)的上图用直角坐标表示飞行过程中目标 P 的雷达回波相位变化图,当 P 点位于飞机的正侧方时,目标 P 到雷达的距离最近,设以这时回波相位为基准(假设为0),而在此前后的相应距离要长一些,即回波相位要加大。而如图1.5(b)的上图所示,不难从距离变化计算出相位变化的表示式,它近似为抛物线。上述相位变化的时间导数即多普勒频率(要除以2π),如图1.5(b)的下图所示,这时的多普勒频率近似为线性变化,图中画出了与航线平行的线上多个点目标回波的多普勒频率变化图,它们均近似为线性调频信号,只是时间上有平移。
在多普勒频率为常数的情况下,可以用傅里叶变换做相干积累,也就是脉冲压缩。现在是线性调频信号,只要调频率已知,对它做脉冲压缩是不困难的。
从图1.5(b)也可以看出,在与飞行航线平行线上的点目标具有相同的冲激响应,而当该平行线与航线的垂直距离不同时,冲激响应也不相同,主要是调频率发生了变化。冲激响应的空变性,给图像重建的计算带来一定的复杂性。
在上面的讨论中,还只是考虑了目标到天线相位中心距离变化引起的相位变化。如果上述距离变化是波长级的,只考虑相位变化就可以了;若距离变化与径向距离分辨单元的长度可以相比拟,甚至长达多个距离单元,这时就要考虑越距离单元徙动的问题,这在1.2.1节讨论逆合成孔径成像技术时已经提到过,不过合成孔径雷达观测的场景通常比逆合成孔径雷达的目标大得多,只要分辨率高一些,越距离单元徙动就可能发生。有关问题将在后面详细讨论。
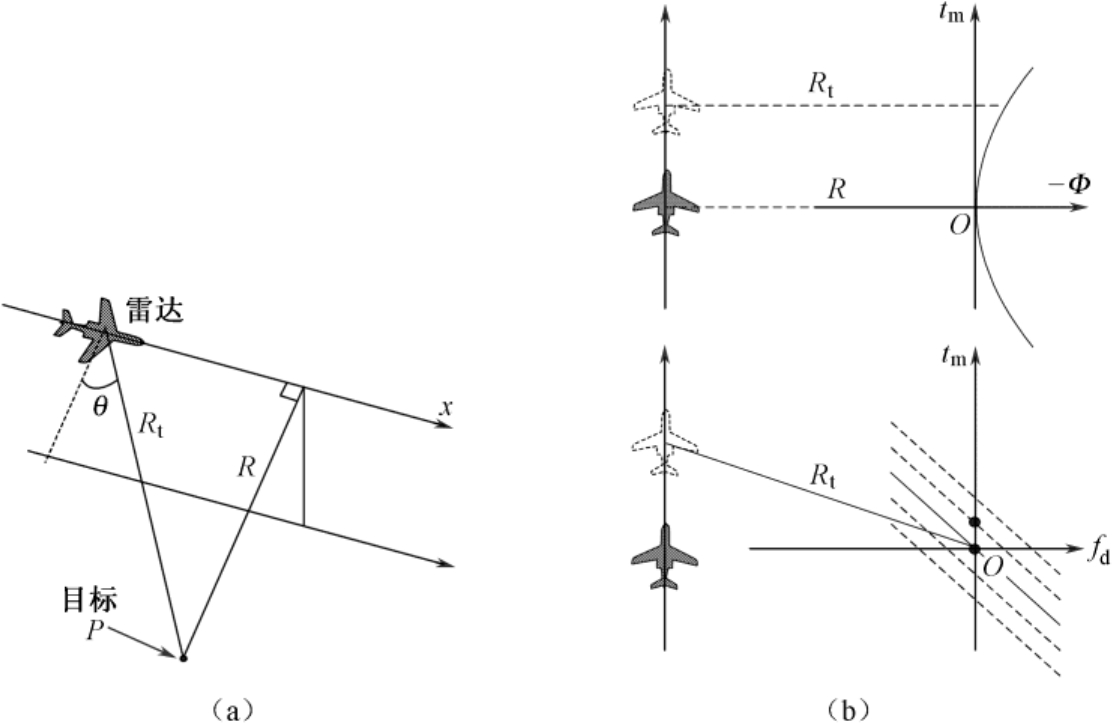
图1.5 SAR成像几何关系以及SAR信号的相位和多普勒频率图
上面是用多普勒效应对合成孔径技术的高的横向分辨率问题做了说明。用合成孔径的概念同样也可做出解释,这里不再重复。下面用合成孔径来说明聚焦和非聚焦问题,由此可以得到更清晰的概念。
在图1.6里画出了飞行航线和场景里的点目标 P ,合成孔径沿航线排列。如果合成孔径较长,应考虑目标 P 回波的波前为球面波。从该图中可见,若波前为平面波,则合成孔径阵列上各阵元的相位相同,将它们直接相加就可重建目标 P 的形状(横向)。但实际波前为球面波,从而造成不同阵元上的信号有不同的相差,只有补偿相差后相加才能正确重建,这相当于光学系统里的聚焦。实际上,这里的聚焦相差补偿也就是多普勒调频率补偿,只是解释方法不同而已。
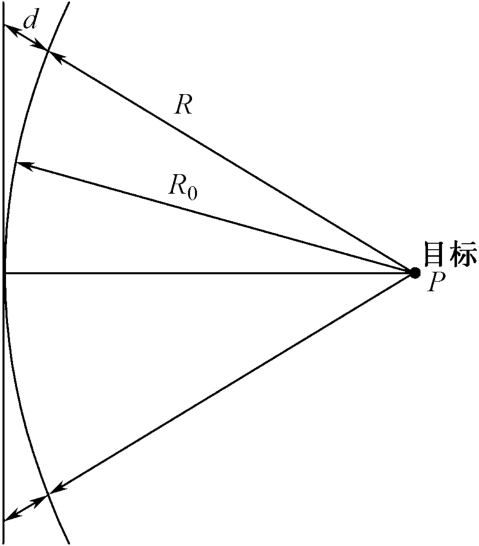
图1.6 合成孔径排列
如果合成孔径长度不长,可用图1.6中与球面波相切的一小段直线近似球面波的弧线,这时可用平面波时各阵元的信号直接相加来近似重建目标,这称为非聚焦方法。
上面提到非聚焦方法的合成孔径只能用“一小段直线”,这“一小段”直线允许多长呢?下面做一些说明:设阵列以
A
为中点,前后对称排列,若波前为平面波,则所有阵元上的信号相位均相同,而在球面波情况下,直线上阵元的信号会有相位差,若仍以
A
点为基准,则偏离
A
点越远,相位差就越大,当相位差大到
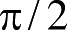 (考虑到收、发双程,即该阵元与球面波前的距离差为
λ
/8)时,再加大孔径而得到的积累增益已经很小,因此通常以到球面波前的距离差为
λ
/8 来确定有效孔径长度。通过简单的几何运算,即可得到非聚焦时的有效孔径长度
(考虑到收、发双程,即该阵元与球面波前的距离差为
λ
/8)时,再加大孔径而得到的积累增益已经很小,因此通常以到球面波前的距离差为
λ
/8 来确定有效孔径长度。通过简单的几何运算,即可得到非聚焦时的有效孔径长度
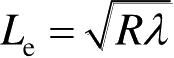 ,
R
为目标距离;并可计算得到这时的横向(方位)分辨率
,
R
为目标距离;并可计算得到这时的横向(方位)分辨率
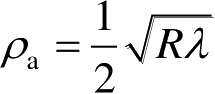 。举一个数字例子,若波长
λ
=3 cm,距离
R
=30 km。这时非聚焦的有效孔径长度
L
e
=30 m,而横向分辨率
ρ
a
=15 m。由于
ρ
a
与
。举一个数字例子,若波长
λ
=3 cm,距离
R
=30 km。这时非聚焦的有效孔径长度
L
e
=30 m,而横向分辨率
ρ
a
=15 m。由于
ρ
a
与
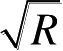 成正比,若距离加长,横向分辨率还要下降。
成正比,若距离加长,横向分辨率还要下降。