




各类飞机目标的RCS显著地依赖于被观察飞机的类型、照射频率和姿态角,同时也与照射波极化有关,因此需要一种规范性的描述。
1. 典型飞机RCS 统计平均值
下面给出3种典型飞机在不同频段上的RCS随方位角的变化曲线,分别如图3.1、图3.2和图3.3所示。
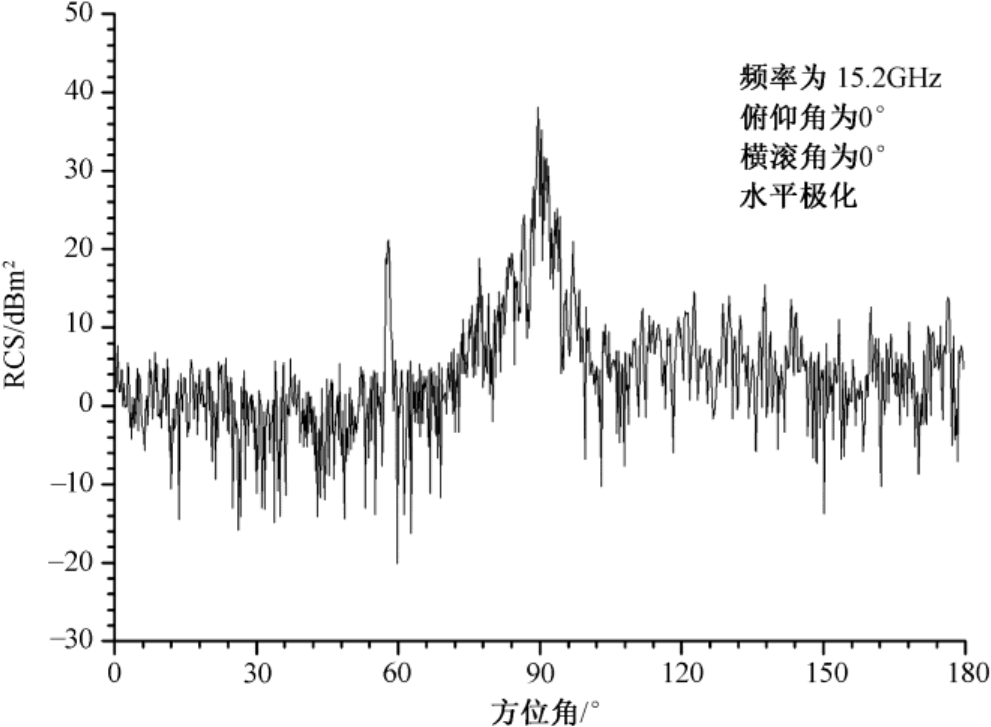
图3.1 某飞机在15.2GHz时的RCS随方位角的变化曲线
图3.1中横坐标方位角0°表示飞机鼻锥方向对准雷达来波,纵坐标RCS的单位为分贝平方米(dBm 2 ),即相对于1m 2 的分贝数。例如,0dBm 2 表示RCS为1m 2 ,10dBm 2 为10m 2 ,20dBm 2 为100m 2 。由图3.1、图3.2和图3.3所示的3条曲线可以得到如下规律性结论:
(1)频率越高,RCS对姿态角越为敏感。经计算,
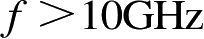 时自相关姿态角小于1°;
f
>1GHz时,计算雷达检测概率时可以认为飞机属快起伏目标;在200~800MHz内,典型飞机处于目标谐振区高端,具有谐振现象,并起伏缓慢。
时自相关姿态角小于1°;
f
>1GHz时,计算雷达检测概率时可以认为飞机属快起伏目标;在200~800MHz内,典型飞机处于目标谐振区高端,具有谐振现象,并起伏缓慢。
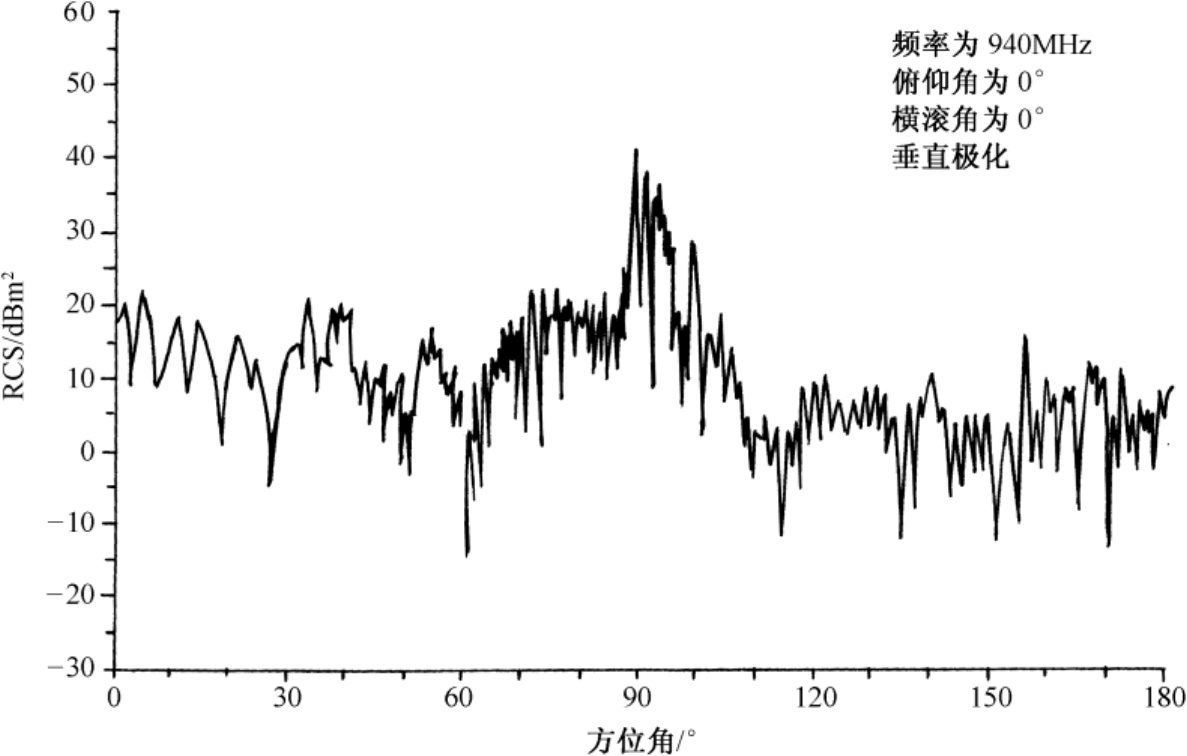
图3.2 波音727-100C飞机在940MHz时的RCS随方位角的变化曲线 [1]
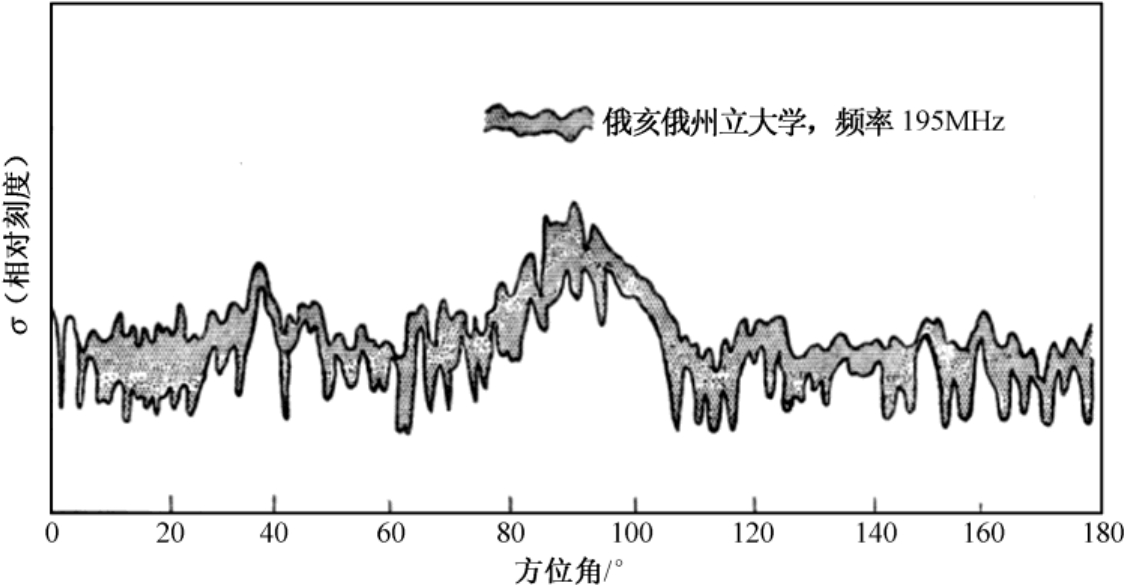
图3.3 B-47飞机在195MHz时的RCS随方位角的变化曲线 [2]
(2)RCS随方位角有规律地变化,通常最小值在5°~20°内(非0°时最小);方位角处于飞机后掠翼前缘法线方向时RCS曲线呈现突增,被称为“突增线”(如图3.1在方位60°处),可用于对飞机翼后掠角的识别;通常在正侧向(方位角90°)RCS最大,可达几百平方米,因此一个飞机目标的RCS起伏动态范围可达40dB。
(3)为规范性描述飞机的RCS,通常以飞机水平状态时,鼻锥方向方位角在0°~45°内统计平均值作为典型RCS值给出。
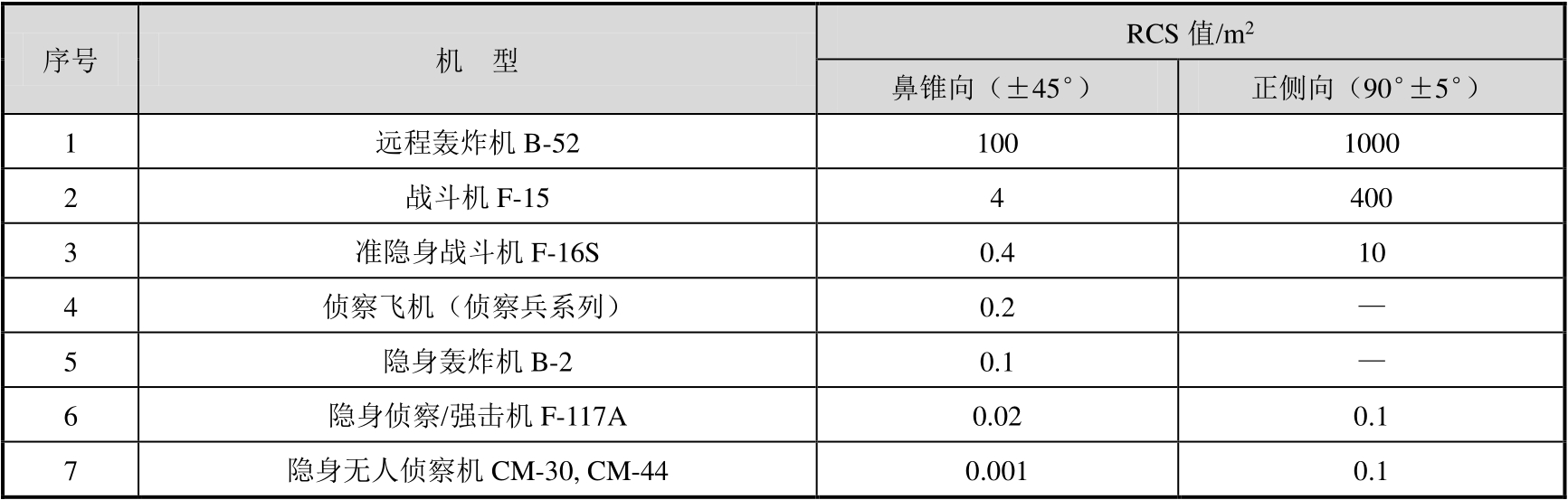
表3.1给出了工作波长 λ = 5cm时各类飞机RCS的典型统计平均值。20世纪50年代开始,各国在设计防空雷达时,其雷达实际作用距离一般按典型飞机目标RCS为4m 2 来确定。随着隐身飞机的工程化和实用化,从20世纪80年代开始,防空雷达设计时的典型飞机目标的RCS一般定为0.4m 2 (相当于准隐身战斗机)。
表3.1 各类飞机RCS的典型统计平均值( λ =5cm时)
2. 飞机RCS 的频率响应
标准散射体与锥球体等目标的RCS明显依赖于频率,可参考图2.6和表2.3。而飞机属于复杂结构形状目标,后向散射较为复杂。由于飞机的低可见度设计一般针对常用的微波频段,因此飞机RCS的频率响应通常两端高,中间低。图3.4所示为一架典型隐身强击/侦察机(类似F-117A型)RCS的频率响应趋势曲线。如图3.4所示,当频率低于200MHz时,RCS有迅速增大的趋势。而在高端,高于16GHz后,RCS也有增大的趋势。
表3.2给出了两种典型飞机RCS统计平均值(鼻锥向±45°)与波段的关系。该表中数值以C波段RCS为准,并参考图3.4的实测曲线经理论估算和验证而得。用该表与表3.1一起可查到其他各类飞机RCS的频率响应变化范围的估值。
表3.2 两种典型飞机RCS统计平均值(鼻锥向±45°)与波段的关系 单位:m 2

值得注意的是,在频率50~400MHz内,飞机目标有可能产生RCS谐振现象,谐振产生的RCS振幅可达10dB左右,但其谐振频率点则随飞机大小与形状而不同。因此有人建议,雷达可采取频率搜索方式探测低可见度飞机目标,一旦探测到,频率搜索停止。图3.5为苏联作者发表的鼻锥向飞行的小型喷气式飞机RCS随频率变化的谐振曲线(对原图坐标单位做了修改) [3] 。对特征尺度大于10m的飞机,其RCS谐振特性发生在小于100MHz的地方。
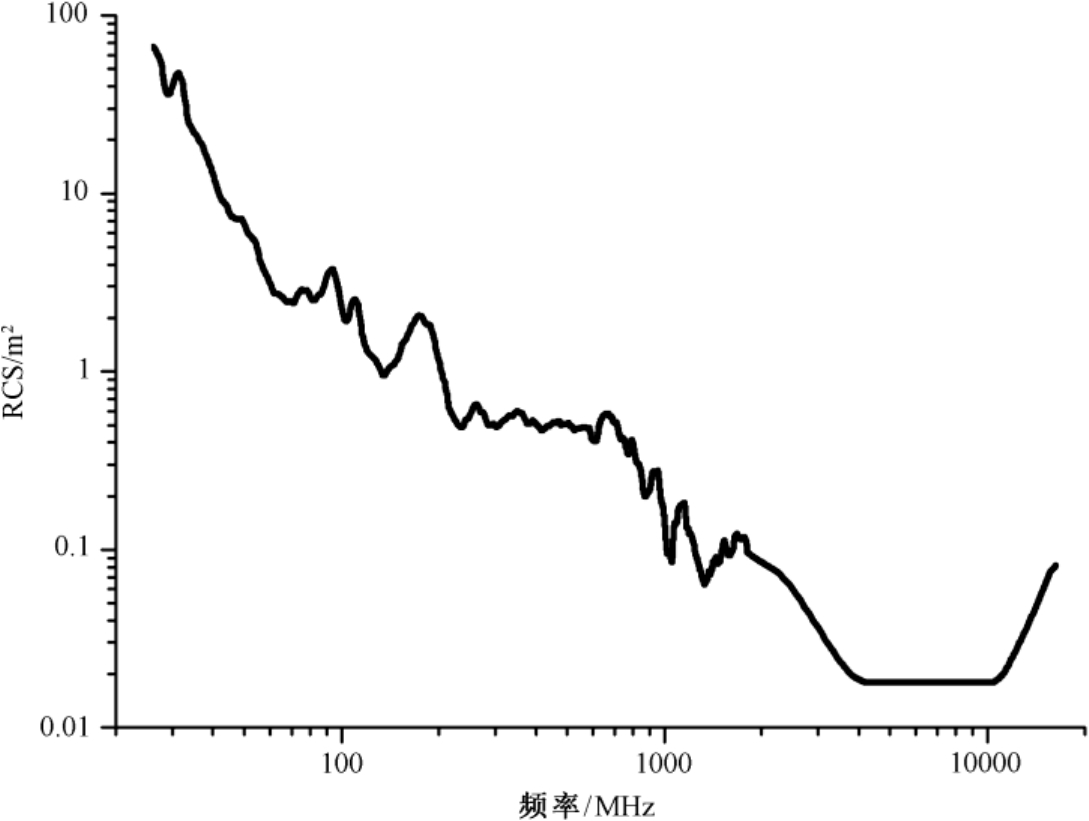
图3.4 一架典型隐身强击/侦察机RCS的频率响应趋势曲线
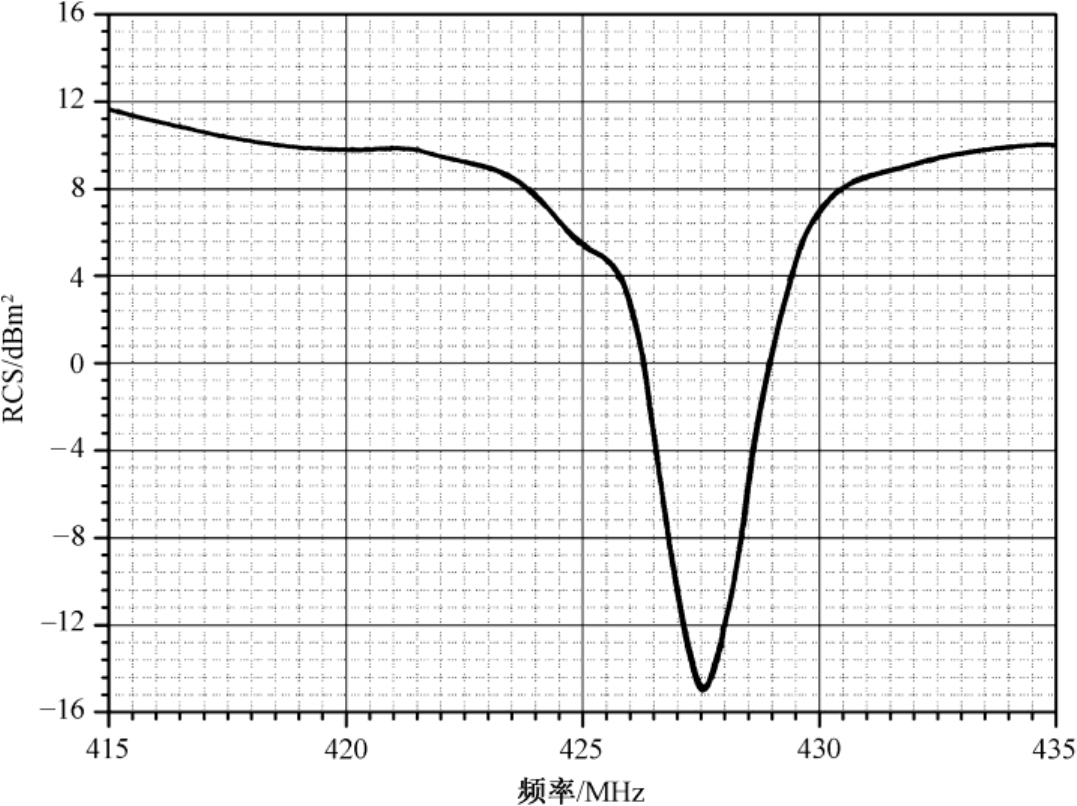
图3.5 小型喷气式飞机RCS随频率变化的谐振曲线
3 . 飞机RCS 的俯仰姿态角响应
由于隐身飞机的低可见度设计不可能在两个欧拉角内均达到隐身,尤其在俯仰平面内有可能观察到大RCS值,因此对于弹载导引头和机载雷达来说,选择俯视观察目标有可能取得良好的反隐身效果。图3.6为一架典型隐身强击/侦察机(类似F-117A型)的RCS测量值随俯仰姿态角的变化曲线。该图中,横坐标俯仰角0°表示飞机鼻锥正视雷达方向。当俯仰角达到52°时,RCS将增大240倍(相对于俯仰角0°)。
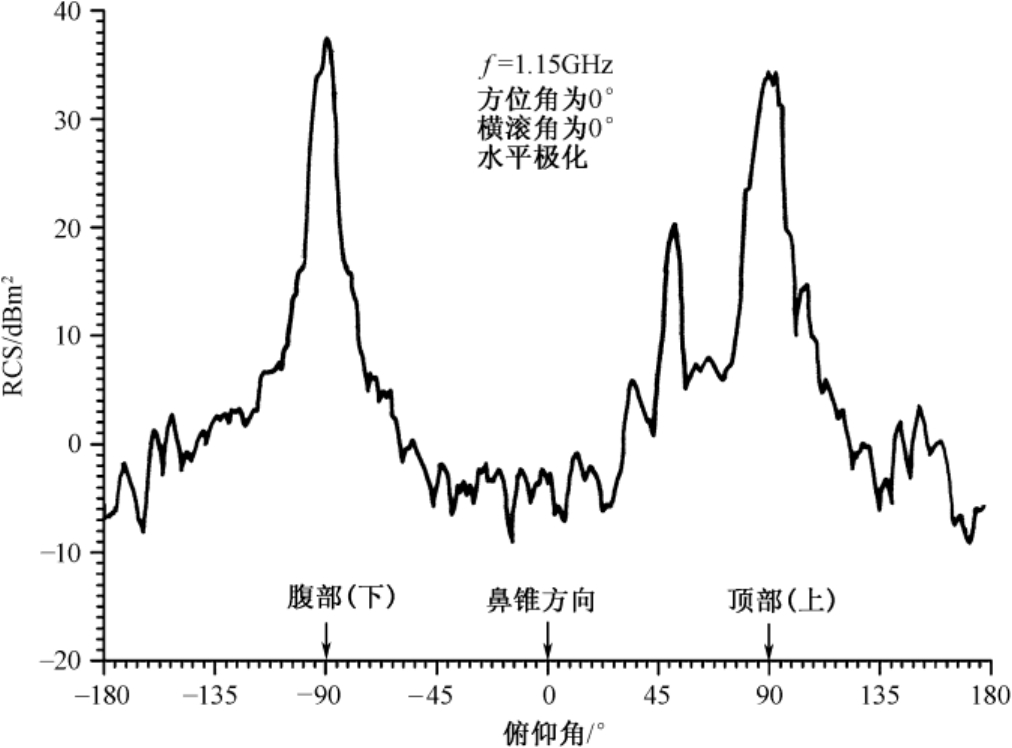
图3.6 一架典型隐身强击/侦察机的RCS测量值随俯仰角的变化曲线
4. 飞机RCS 的双基地特性
对低可见度飞机目标探测时,有时要采取大双基地角来反隐身。图3.7所示为一架典型隐身强击/侦察机(类似F-117A型)双基地RCS随双基地角变化的计算曲线。由该图可见,当双基地角大于120°后,双基地RCS值显著地增大,这是由于产生前向散射机理的缘故。该图表示,一架单基地RCS为0.9m
2
的隐身飞机,在双基地角
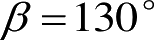 时,其双基地RCS可达14.7m
2
。
时,其双基地RCS可达14.7m
2
。
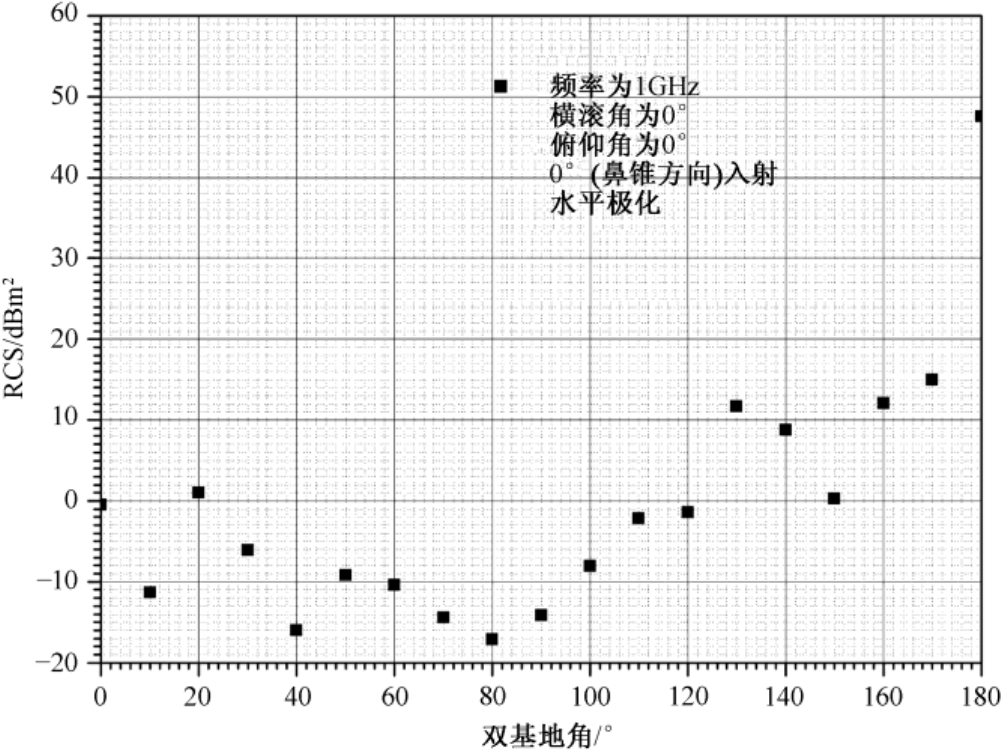
图3.7 一架典型隐身强击/侦察机双基地RCS随双基地角变化的计算曲线
图3.8以曲线方式给出了在C、Ku和X波段,对俯仰角为0°时测量的“哈姆”反辐射导弹模型的两种极化RCS随方位角变化的情况。注意 ϕ =180° 代表鼻锥方向。数据经过4°窗口和1°步长的平滑。图3.9所示为该导弹模型的三视图。
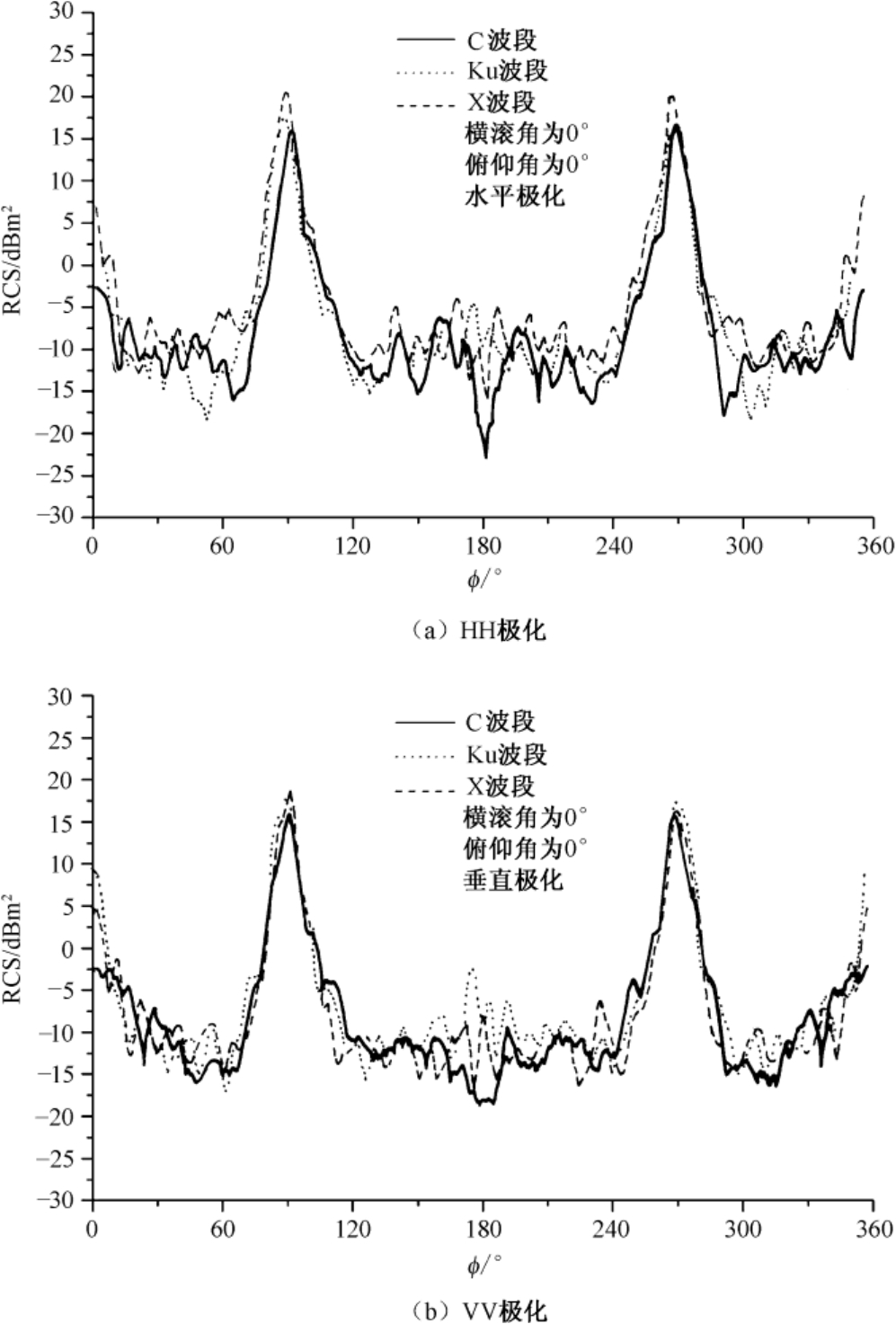
图3.8“哈姆”反辐射导弹模型的两种极化RCS随方位角变化的情况
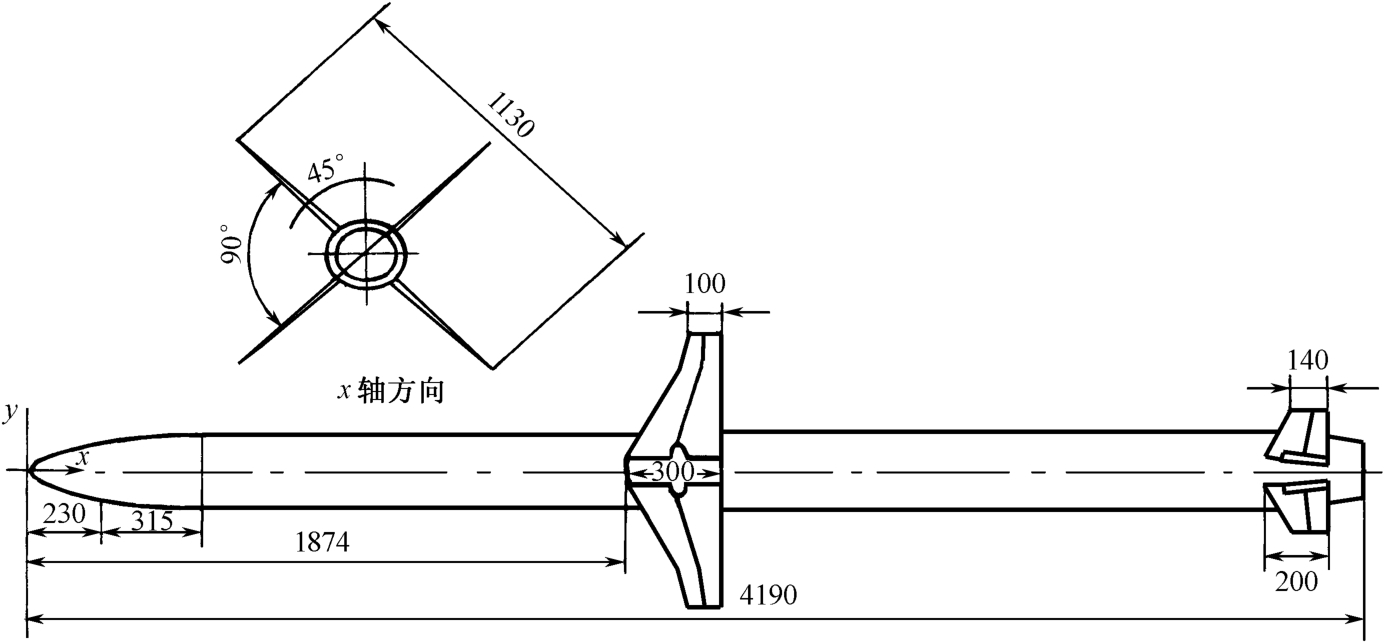
图3.9“哈姆”反辐射导弹模型的三视图(尺寸单位为mm)
图3.10和图3.11以曲线方式分别给出了在C、S和Ku及X波段上,对俯仰角为0°时测量的“幼畜”空地导弹模型的两种极化RCS随方位角变化的情况。方位角 ϕ =180° 代表鼻锥方向。数据经过4°窗口和1°步长的平滑。图3.12所示为该导弹模型的三视图。
为了便于利用,表3.3给出了由图3.8、图3.10和图3.11归纳的俯仰角为0°时“哈姆”反辐射导弹和“幼畜”空地导弹头部(
ϕ
=180°)和正侧部
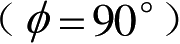 RCS(±45°平均)的参考值。
RCS(±45°平均)的参考值。
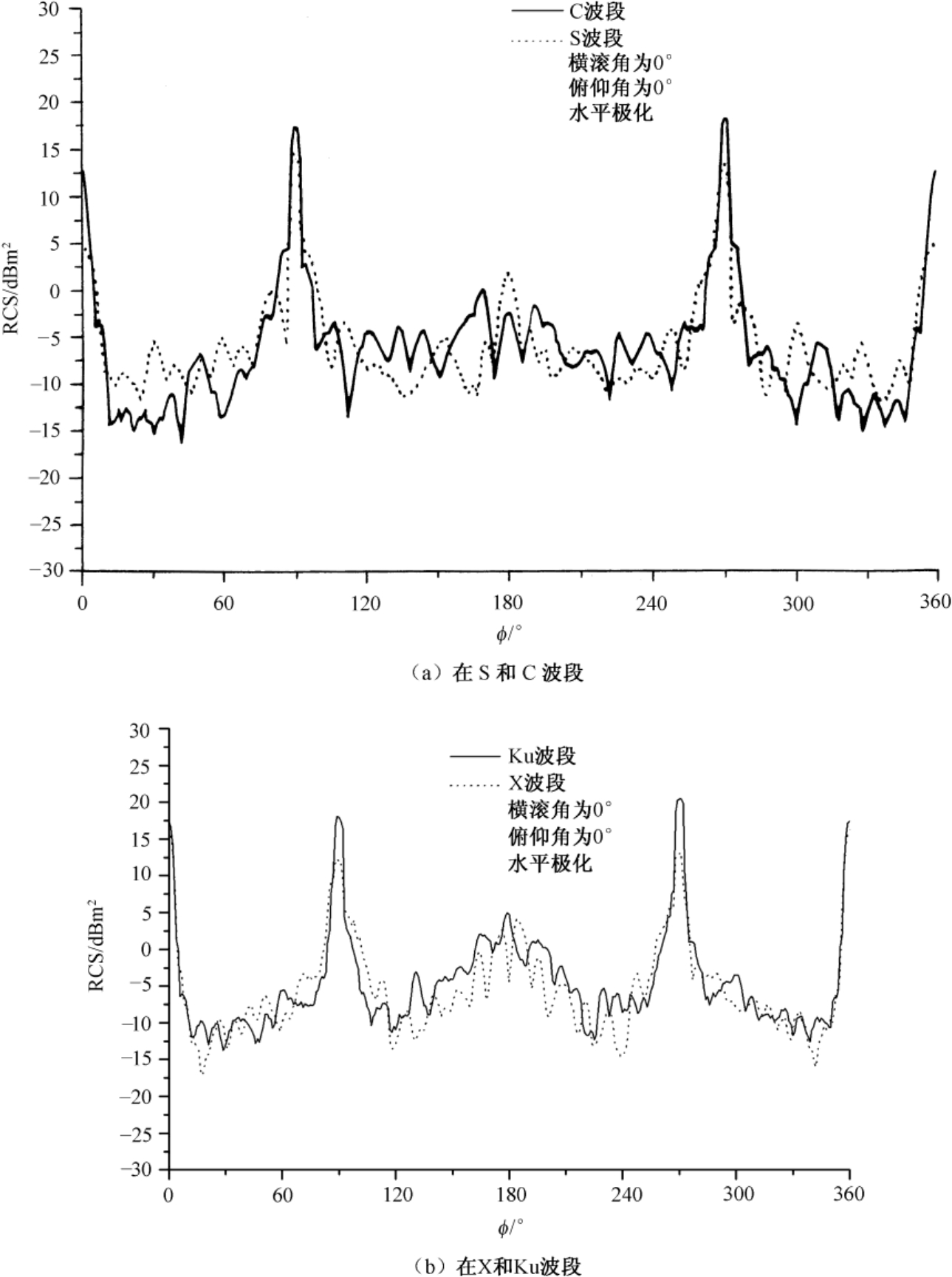
图3.10“幼畜”空地导弹模型的HH极化RCS随方位角变化的情况
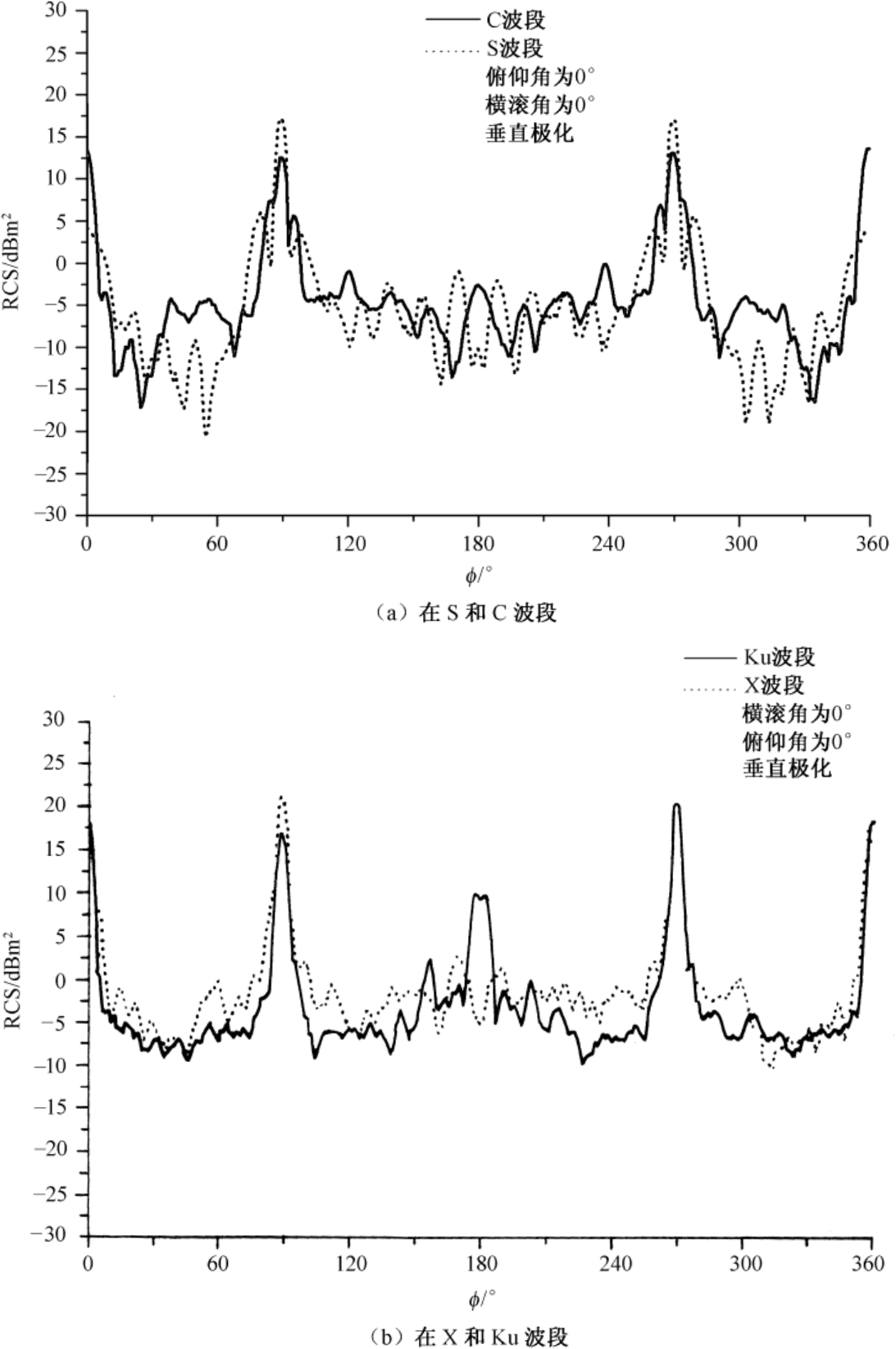
图3.11“幼畜”空地导弹模型的VV极化RCS随方位角的变化
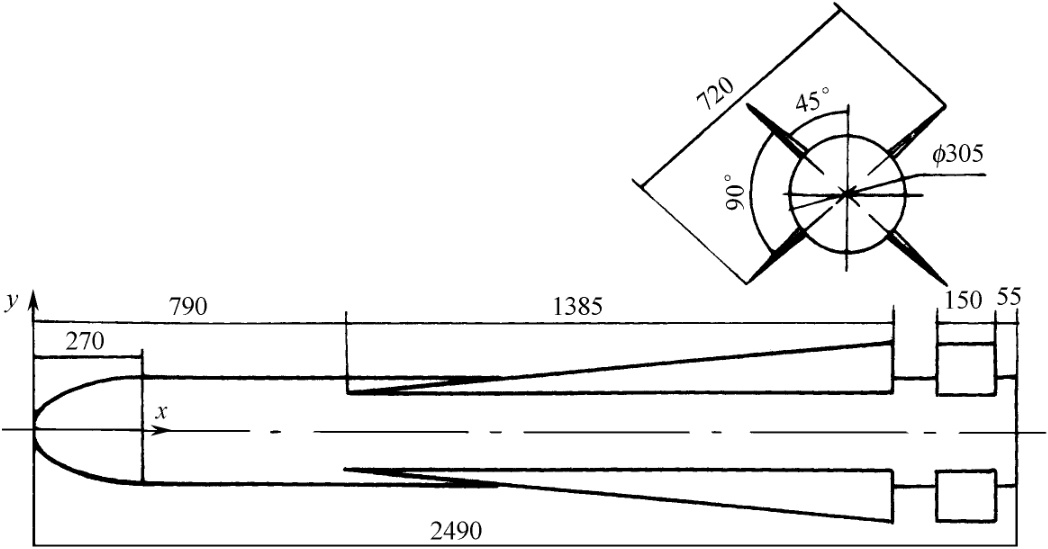
图3.12“幼畜”空地导弹模型的三视图(尺寸单位为mm)
表3.3“哈姆”反辐射导弹和“幼畜”空地导弹头部/正侧部RCS的参考值
单位:m
2
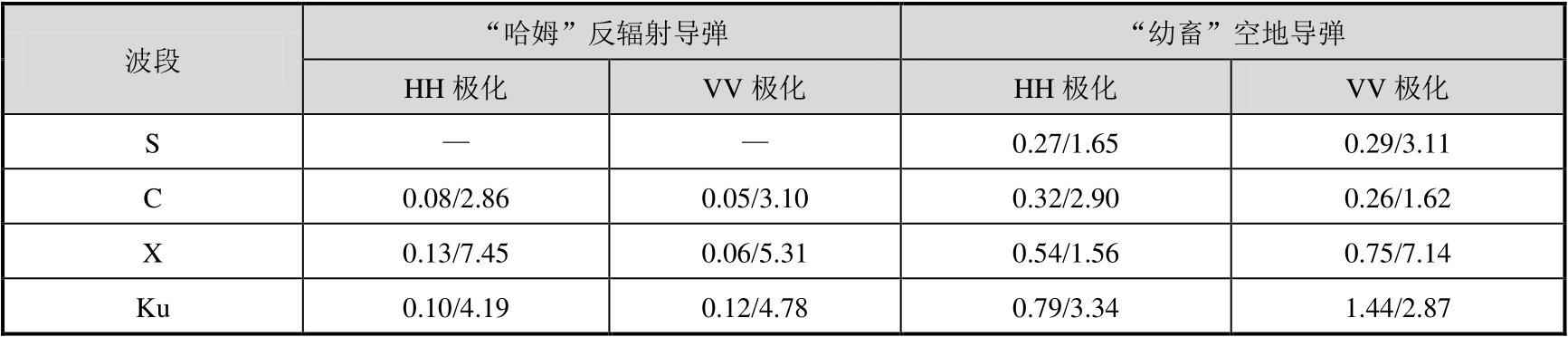
由表3.3可见,对于受攻击的雷达(处于头部),空地导弹目标RCS在主要微波波段范围内应按0.1m 2 设计,侧向观察可按2~4m 2 设计。
图3.13以曲线方式给出了在C、S、Ku和X波段上对俯仰角为0°时,测量的“战斧”巡航导弹模型的两种极化RCS随方位角变化的情况,其数据经过4°窗口和1°步长的平滑。表3.4给出了归纳的“战斧”巡航导弹头部( ϕ =180°)和正侧部( ϕ =90°)RCS(±45°平均)的参考值。请注意,由于模型是完纯导体,所以该表中的结果应该认为是没有隐身吸波涂层贡献的结果。吸波涂层可能使RCS再降低5~8dB。因此,对于受攻击的雷达,巡航导弹RCS在主要微波波段范围内应按0.1m 2 设计,侧向观察按2m 2 设计。
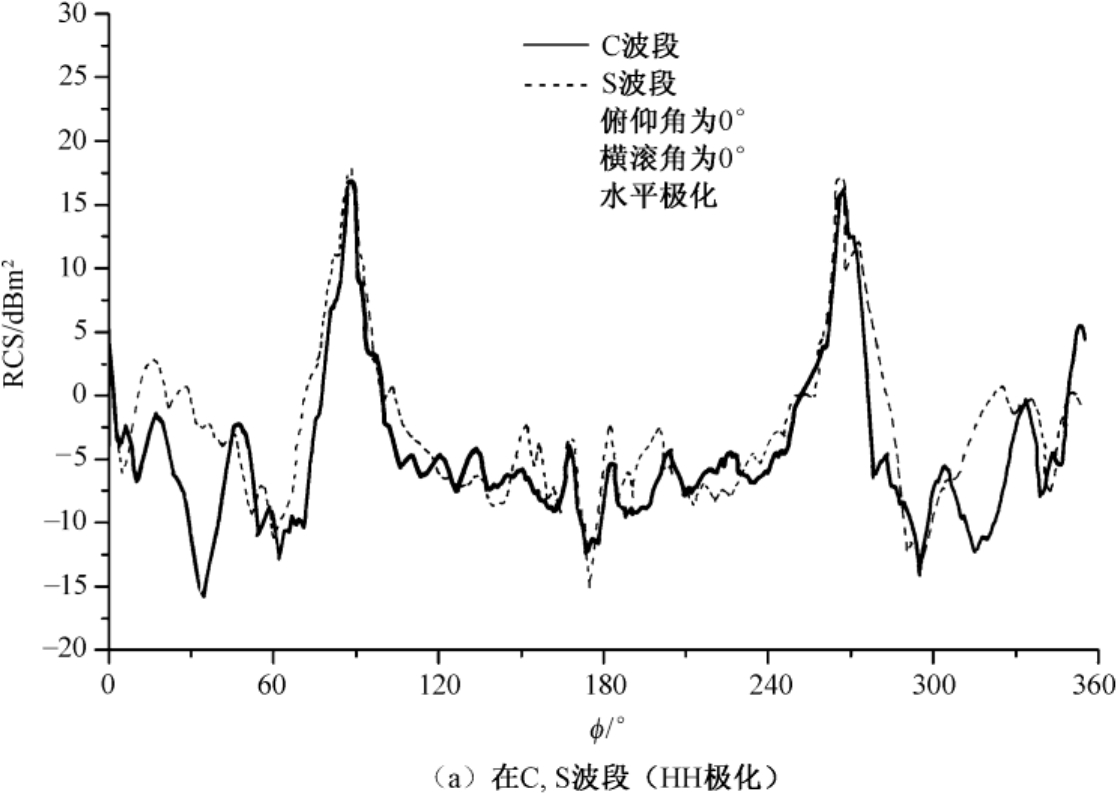
图3.13“战斧”巡航导弹模型的两种极化RCS随方位角变化的情况
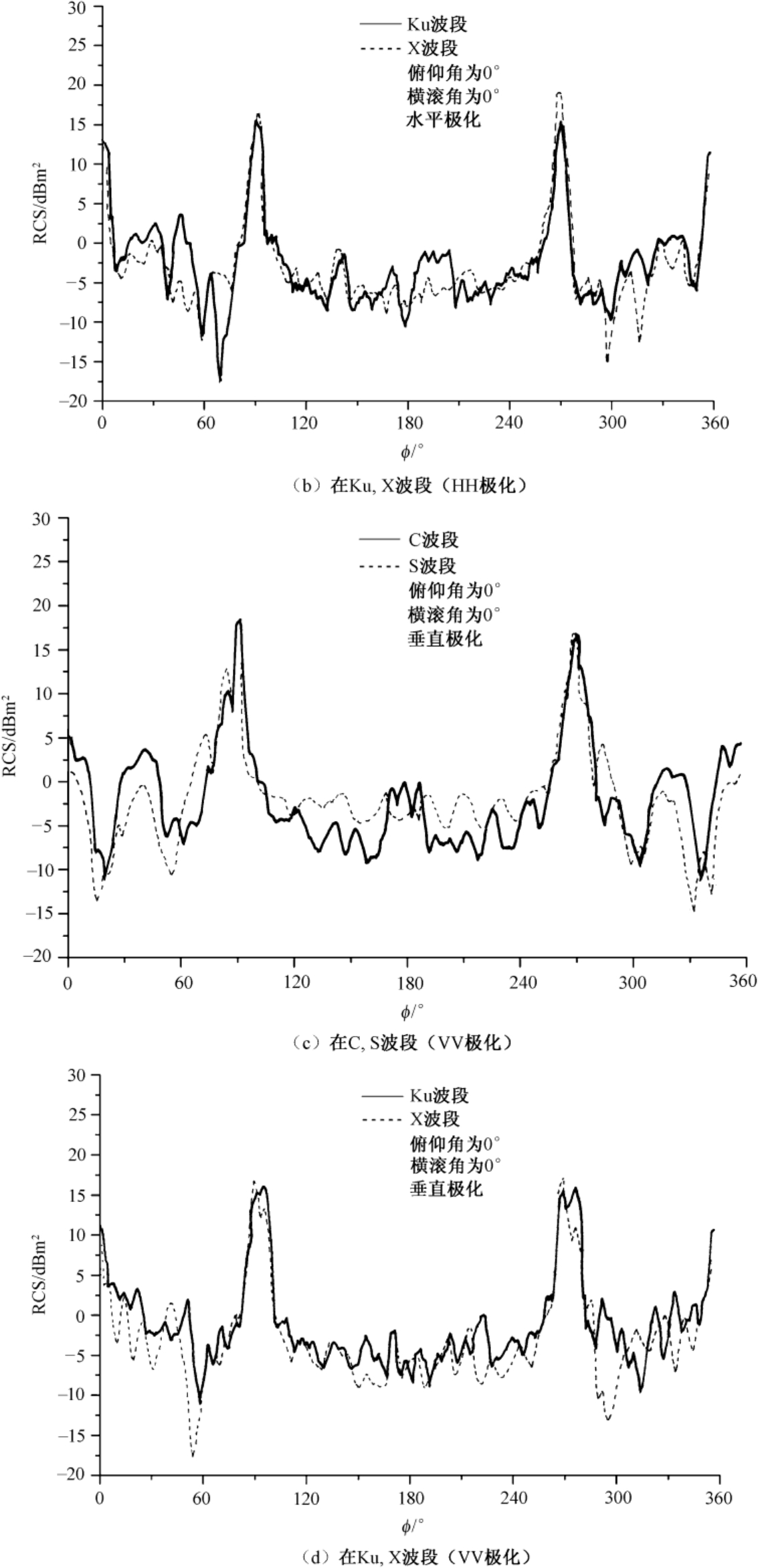
图3.13“战斧”巡航导弹模型的两种极化RCS随方位角变化的情况(续)
表3.4“战斧”巡航导弹头部/正侧部RCS(±45º平均)的参考值单位:m 2

注:该数据不包括隐身吸波涂层的贡献。
对地基和空基雷达来说,地球表面相当于一种杂波源。因此,必须(至少是粗略地)知道沙漠、耕地、户外树林、有树林的小山等的雷达回波的量级。表3.5所示为不同地形类型散射截面的每平方米平均RCS的测量值(以1m 2 为参考值,单位为dBm 2 ) [4] 。
表3.5 不同地形类型的每平方米平均RCS的测量值 单位:dBm 2
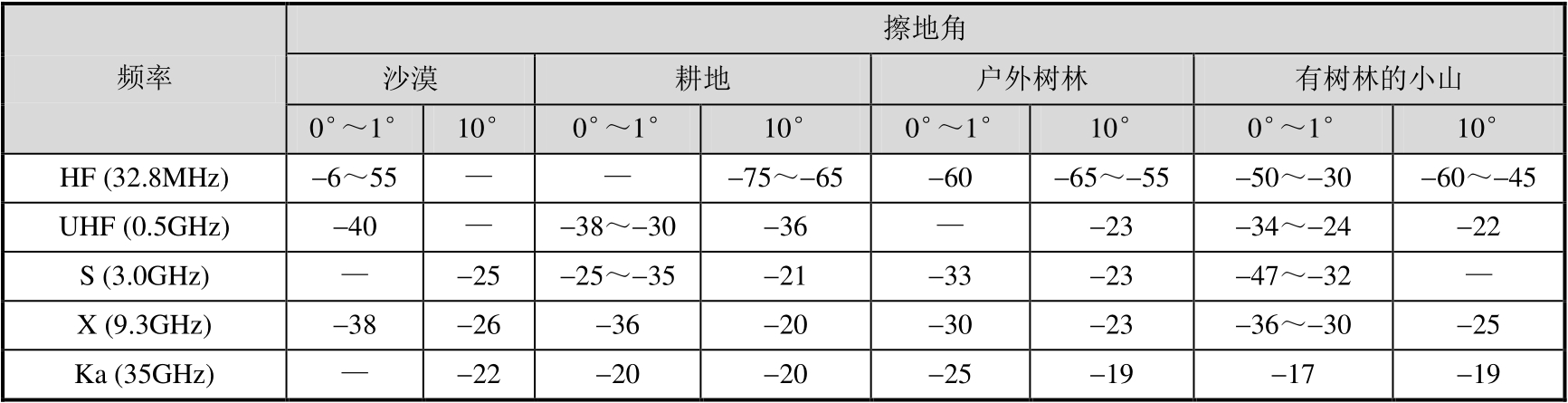
雷达工程师经常对诸如建筑物,甚至城市之类的城市建筑的散射感兴趣。表3.6是对不同频率和擦地角测量的小建筑物和城市每平方米的平均RCS [4] 。该表中的参数是每单位表面面积的平均后向散射截面,用 γ 表示,以1m 2 为参考值,单位为dBm 2 。当入射面与两座建筑物中的一座重合时,道路平行和垂直的城市一般比道路不规则城市的RCS要大得多,这可能是因为在地面和建筑物的外墙之间形成了角反射器的缘故。
表3.6 对不同的频率和擦地角测量的小建筑物和城市每平方米的平均RCS 单位:dBm 2
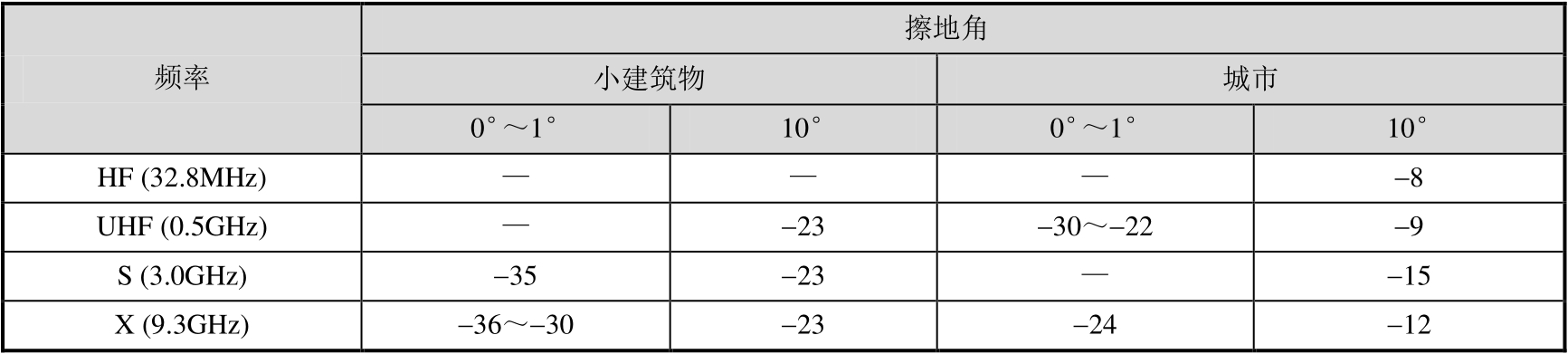
海面也是一种有重要意义的自然目标。海面散射的信息对海背景下雷达目标的检测和识别是必需的。由于风速或海面结冰,海面条件在一天和一年内都会有明显的差别。有关海面散射的文献很多,这里只能涉及其中很少的一部分。海面散射早期的解析模型可在文献[2]中找到,文献[5-7]讨论了严格的解析模型。表3.7是在不同的频率和掠射角(或俯角)下,对不同风速测量海面的每单位面积的平均同极化的RCS [4] (即散射系数)。
表3.7 对不同的掠射角(或俯角)下对不同风速测量海面的每单位面积的平均同极化的RCS 单位:dBm 2
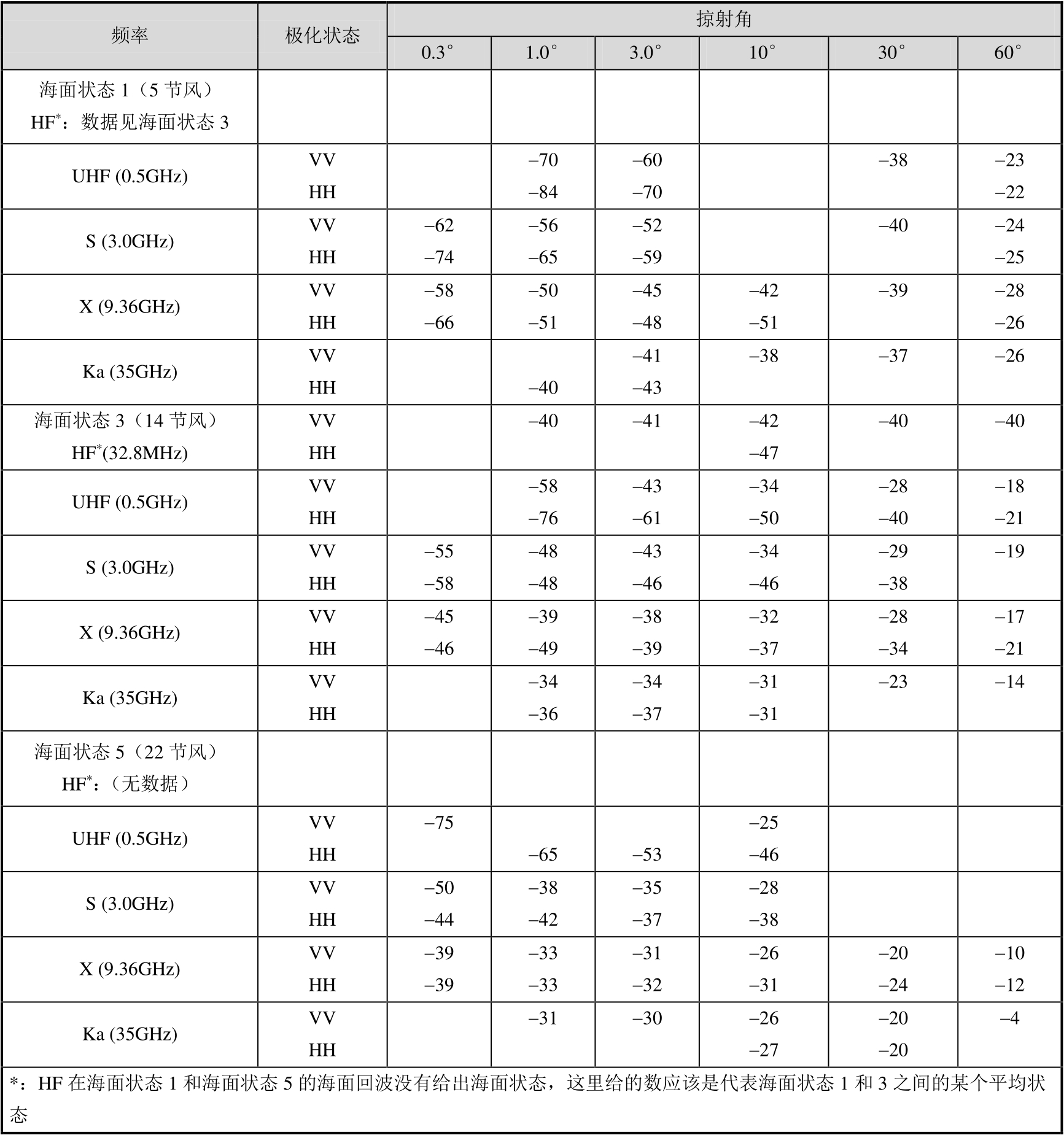
图3.14和图3.15分别是频率为428MHz和4.455GHz时,两种极化下海面的理论RCS和测量RCS的比较,单位为dBm 2 ,按1m 2 归一化。这里给出的RCS数据来自Daley等的测量结果 [5] ,以及组合表面散射模型的理论结果 [6] 。两图中指出的条件是雪天。
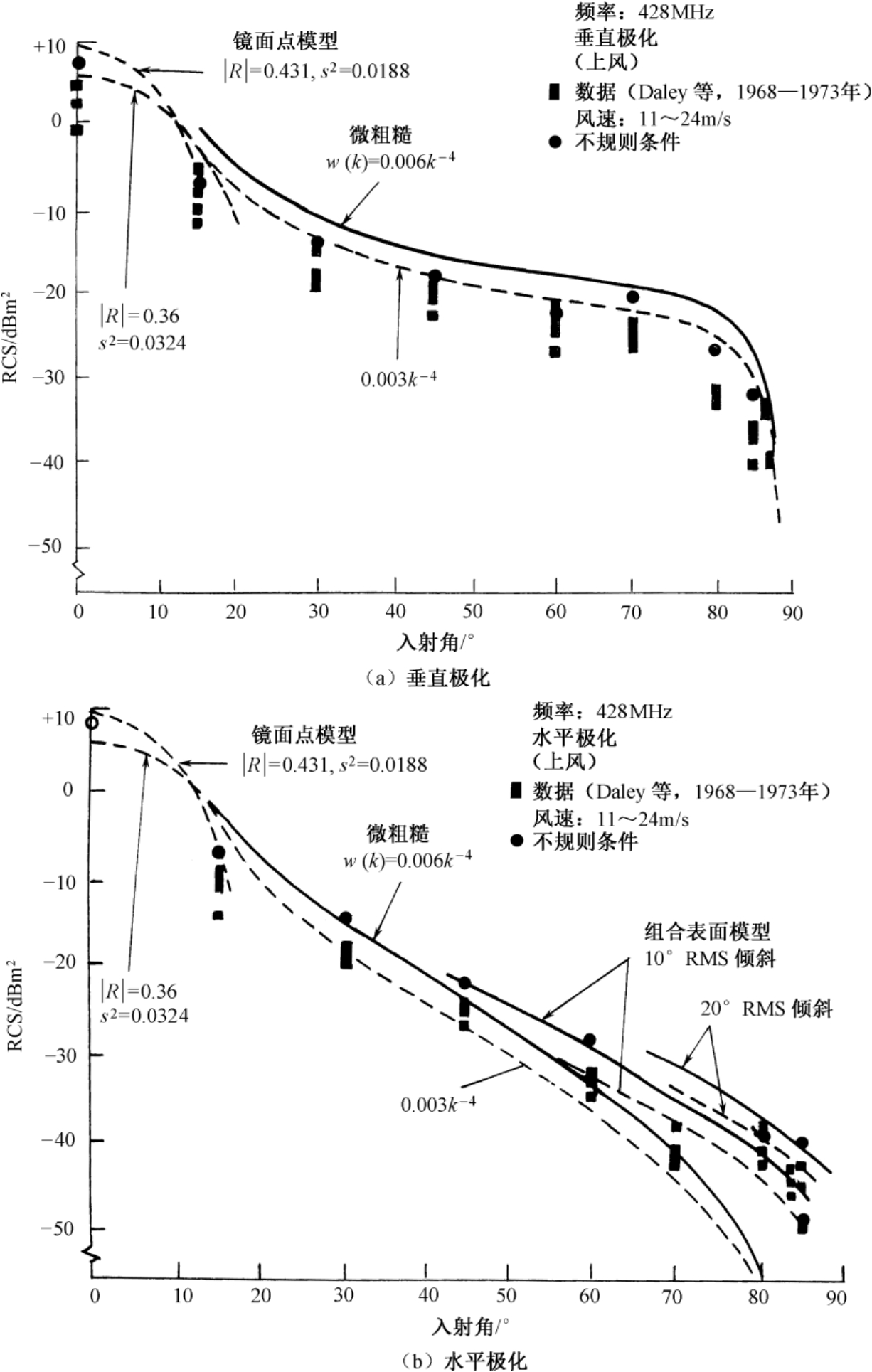
图3.14 频率为428MHz时两种极化下海面的理论RCS和测量RCS的比较
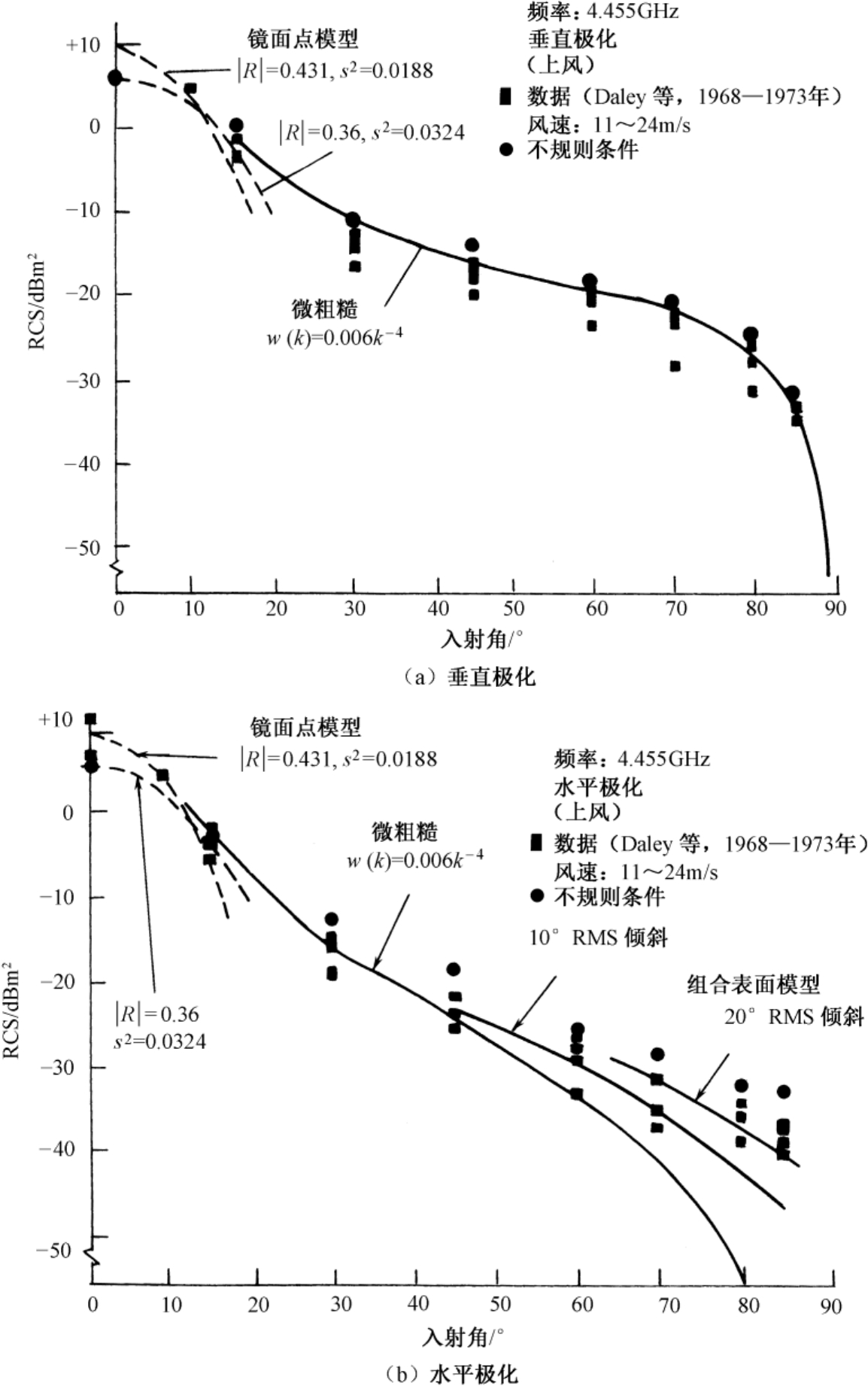
图3.15 频率为4.455GHz时两种极化下海面的理论RCS和测量RCS的比较
在雷达检测空中目标以及测定目标的位置时,经常会遇到飞鸟的回波出现在雷达显示器上,这使得正确检测变得困难。通过在厘米波段对飞鸟之类的雷达目标进行分析,可以发现,鸟体能反射70%以上的入射射频(RF)能量,而羽毛消耗其余的能量 [3] 。在厘米波段鸟羽毛的介电常数大约是1.34,图3.16画出了在18°仰角上观察的几种鸟的RCS曲线。鸟的RCS方向图表明,最大RCS出现在侧边角度上,即沿着鸟翅膀看的时候。实验数据显示出翅膀跨度对鸟的RCS几乎没有影响 [3] 。
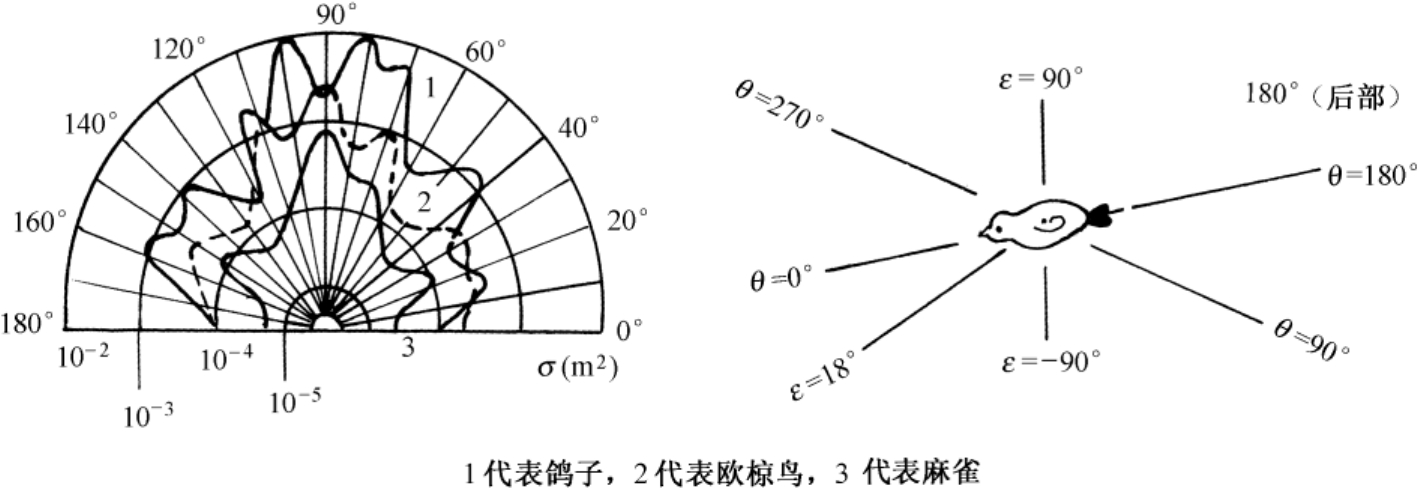
图3.16 在18°的仰角上观察的几种鸟的RCS曲线
鸟的RCS与它们的质量之间存在一种联系 [8] :例如,在S波段(2~4GHz)的垂直极化测量表明,质量为70g的欧椋鸟的平均RCS为10 -3 m 2 ,而质量为1kg的野鸭的平均RCS为10 -2 m 2 。
鸟的回波用不同的幅度调制来表征,调制频率反比于鸟的大小。从燕子到苍鹭不同种类的鸟,按鸟大小有2~10Hz的翅膀拍动频率 [8] 。飞行中,在翅膀拍动一定数量之后,有一定的休息时间,即没有翅膀拍动飞行时,对应于无回波起伏。鸟的速度在32~56km/h(9~15m/s)范围变化。
文献[9]给出了计算单只鸟的RCS理论计算公式为
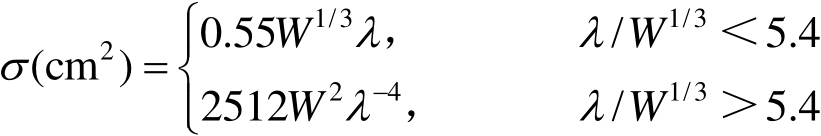
(3.1)
式(3.1)中, W 是鸟的质量,单位为g; λ 是波长,单位为cm。一些成年鸟的典型质量及其RCS如表3.8所示。图3.17给出了频率为1200MHz和400MHz时单只鸟的平均RCS随鸟质量的变化曲线。
表3.8 一些成年鸟的典型质量及其RCS
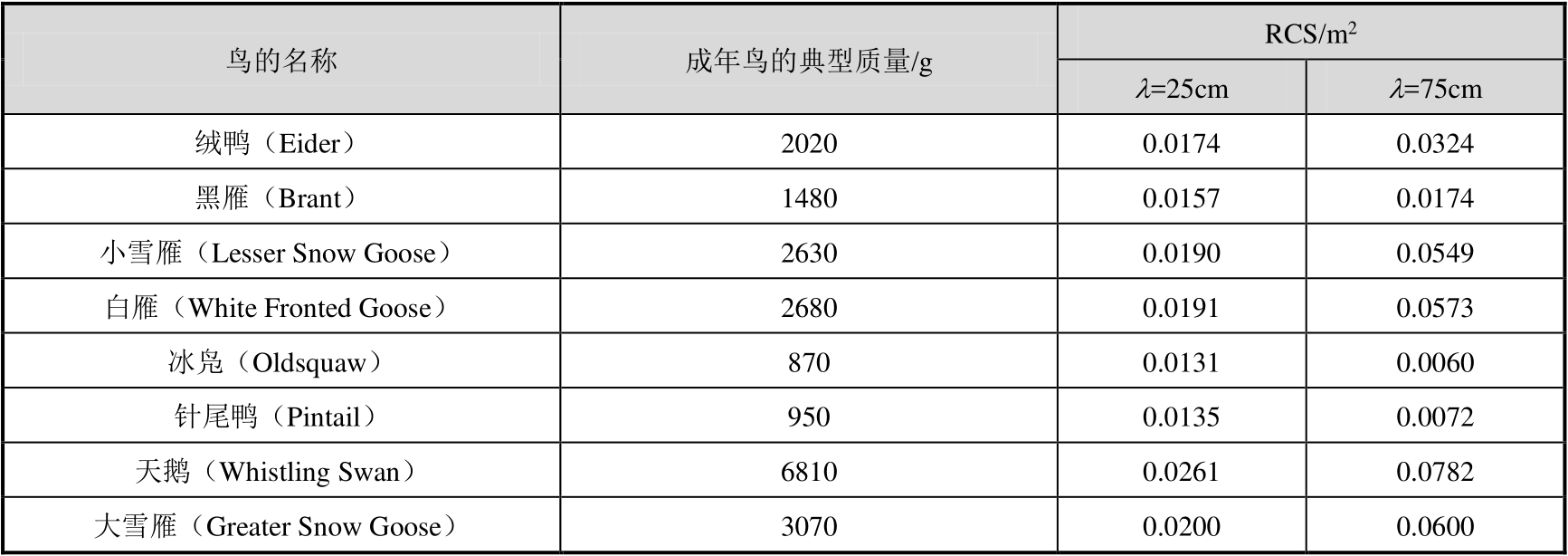
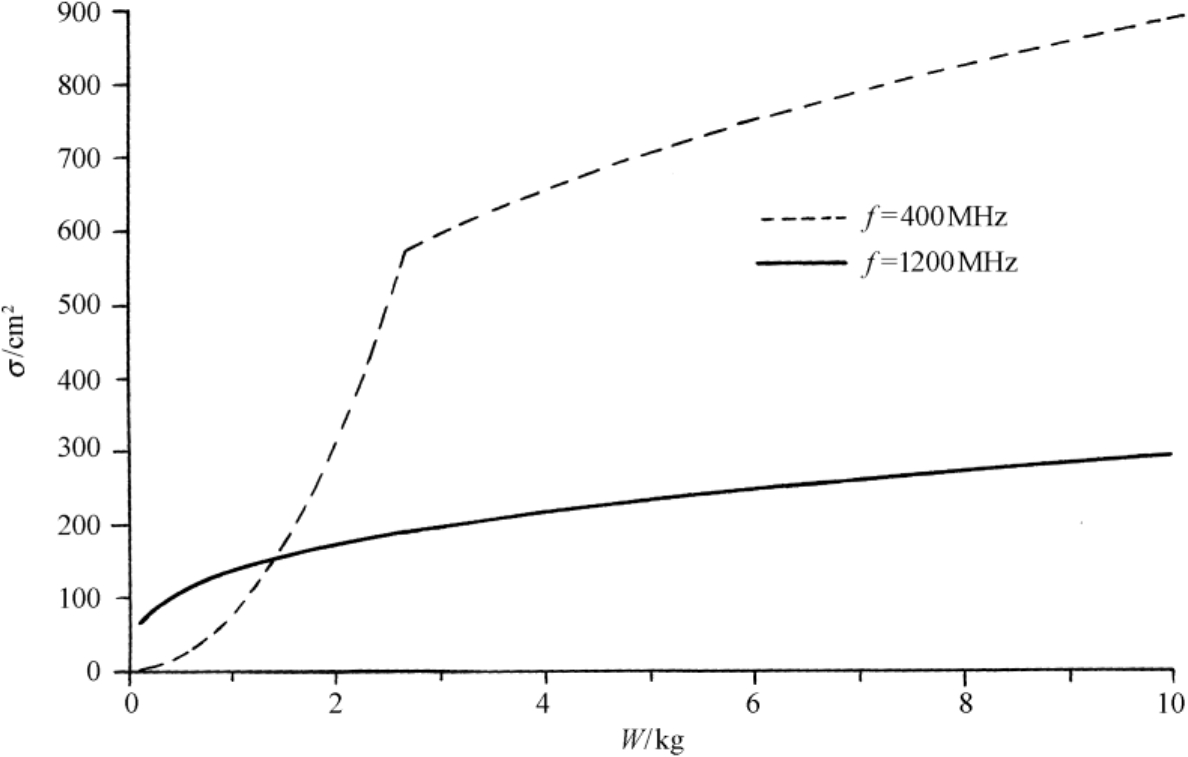
图3.17 频率为1200MHz和400MHz时,单只鸟的平均RCS随鸟质量的变化曲线
实际上人们更感兴趣的是鸟群的RCS。表3.9给出了通常情况下鸟群的密度(单位分辨率内鸟的数量)。根据鸟群的密度,可以推算鸟群的RCS。作为最简单的近似,假设鸟的分布是随机的,但取向是朝同一方向飞行,忽略鸟之间的互耦影响,可以认为鸟群的散射场是考虑相对于观察点波程差后各只鸟平均RCS的复数和,经取模值后得到鸟群的RCS。
表3.9 典型鸟群的密度
Blacksmith和Mack对成年鸭子的RCS进行了测量 [10] 。实验结果整理成统计形式如图3.18所示。结果表明,一只成年鸭子的RCS约为-12dBm 2 。
Mack等在1166MHz的频率上对1.8kg的鸭子和4.9kg的鹅进行了RCS测量 [11] 。结果表明,鸭子的水平RCS在0.02~0.048m 2 之间,垂直RCS在0.001~0.02m 2 之间;鹅的水平RCS在0.07~0.28m 2 之间,垂直RCS在0.0017~0.18m 2 之间。
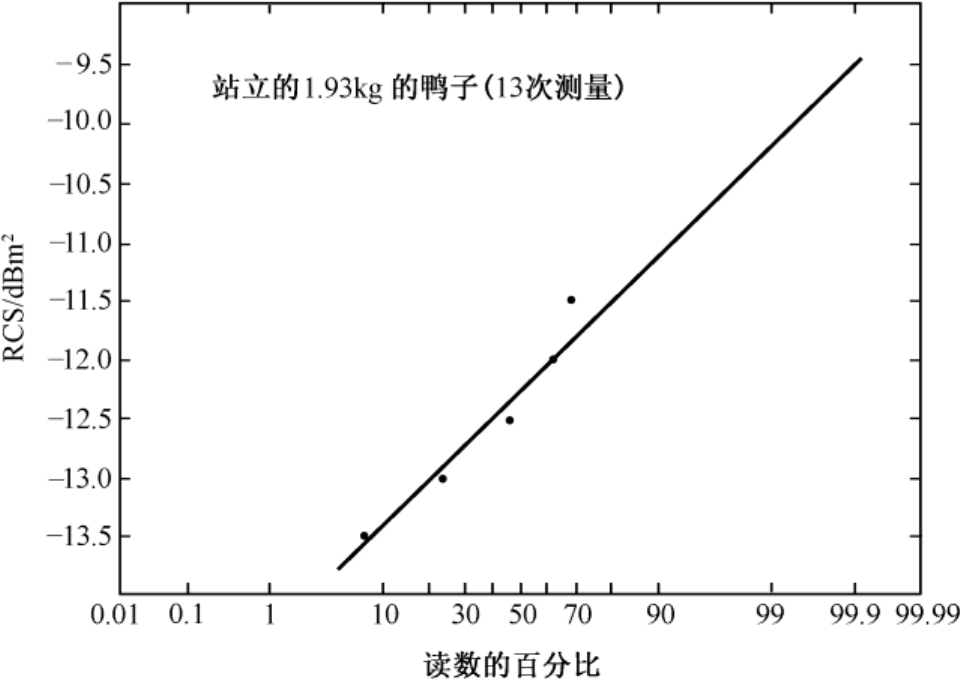
图3.18 Blacksmith和Mack测得的成年鸭子的RCS
Hajovsky等人曾在得克萨斯大学进行了一系列的实验 [12] ,用于确定昆虫回波的大小。实验收集了10种不同的昆虫,长度为5~20cm不等。实验用的是简单的CW测量系统,在9.4GHz频率上进行测量。测量结果汇总于表3.10中。
表3.10 9.4GHz时不同昆虫种类的RCS
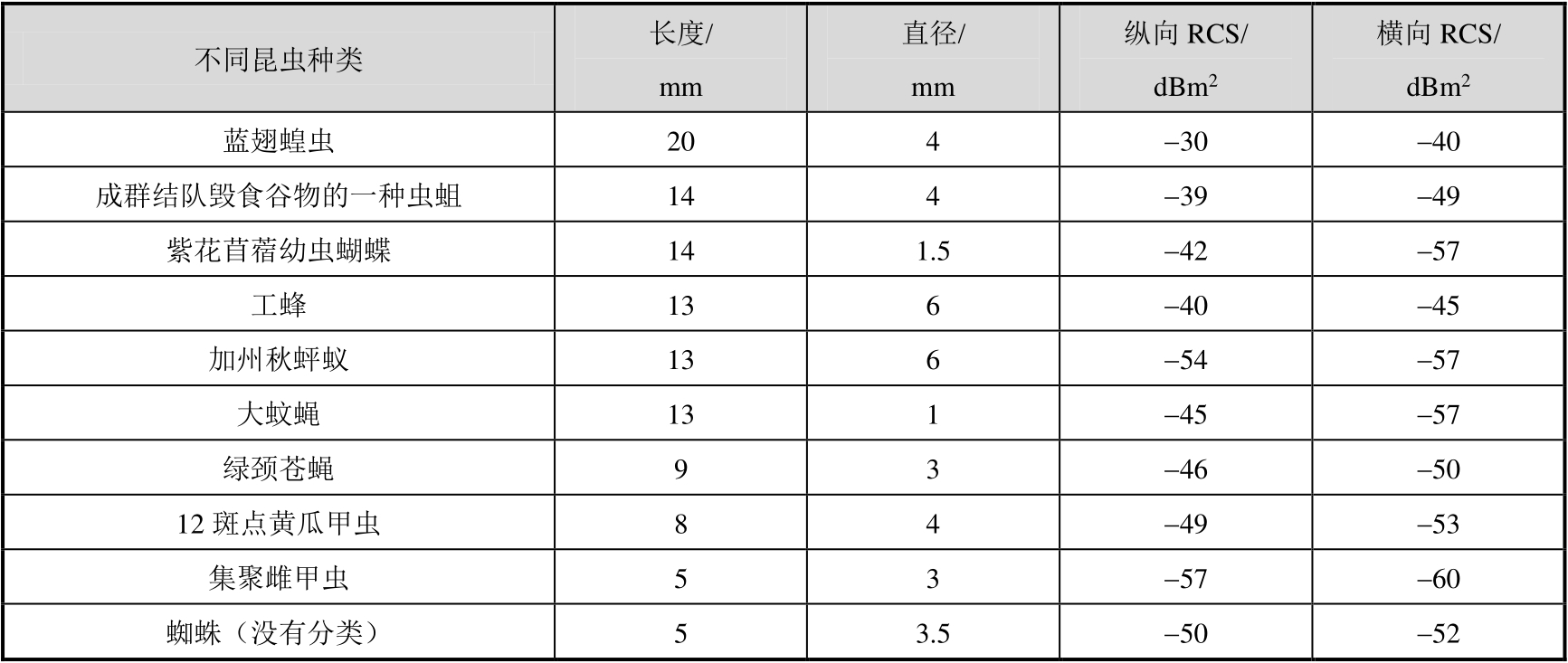
实验表明,昆虫回波的大小既随昆虫的体长尺寸而增大,也与角度有关。从头部入射和侧边入射测量昆虫的RCS,对于长而细的昆虫,纵向(侧面)RCS比横向(顶部)RCS大15dB;而对纵横差不多的昆虫,其纵向和头部RCS之差不大于2dB。
作为雷达目标的人,其散射特征经常是值得注意的(见图3.19)。实验表明,在RCS和质量之间存在正比的关系,人体RCS也与雷达频率有关系 [2] 。
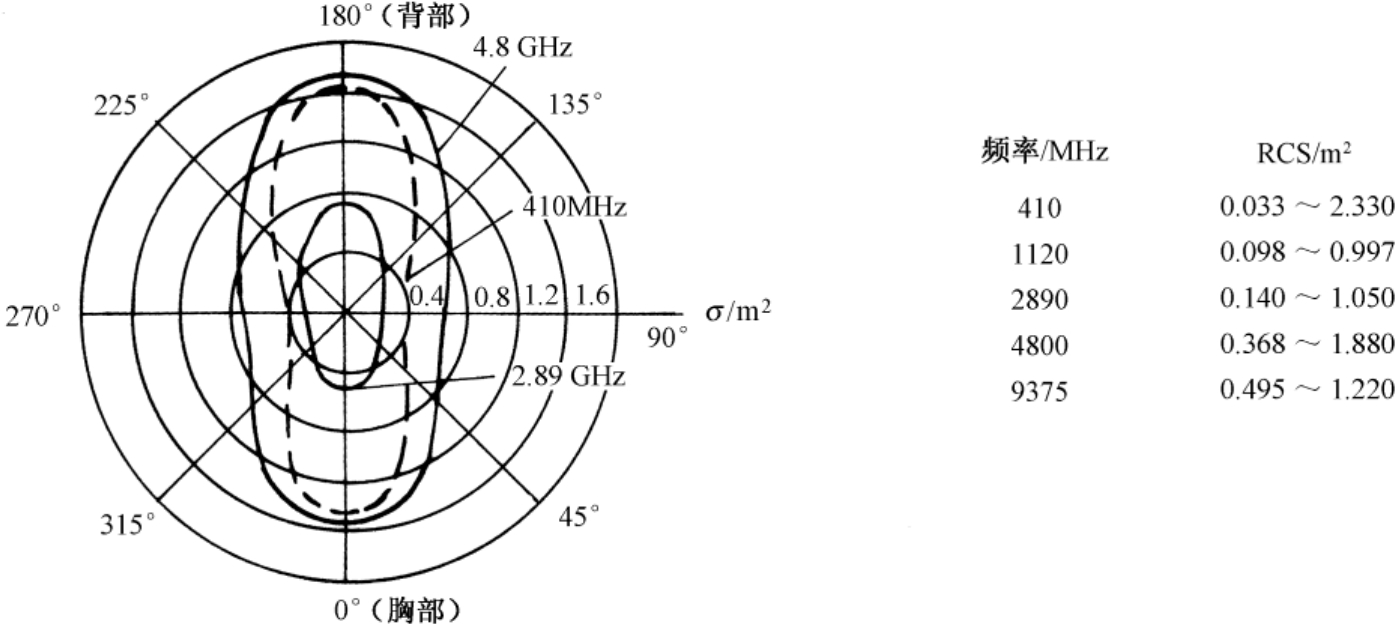
图3.19 在不同的频率上人的垂直极化实验的RCS方向图