




在用测量方法求得各种目标RCS时,需要有一个已知RCS的定标体进行相对标定,因此必须掌握几种不同量级的定标体RCS精确值,这在工程上具有很大的实用价值。
不论在瑞利区、谐振区或光学区,金属导电球是最有用的定标体。下面列出精确级数解的公式,利用计算机进行精确的数值计算,给出金属导电球后向RCS的粗精曲线图。因为它很有用,所以将其数据表列于本书附录B。有关公式推导从略,读者可参阅文献[18, 93]。
略去时谐因子
 后,金属导电球的后向RCS计算公式为
后,金属导电球的后向RCS计算公式为
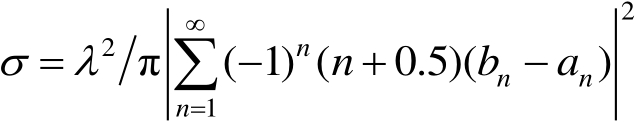
(2.110)
式(2.110)中, a 为导电球半径; λ 为雷达工作波长,且
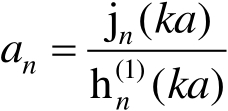
(2.111a)
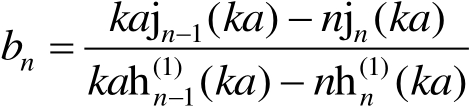
(2.111b)
式中,
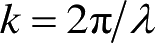 为波数;
为波数;
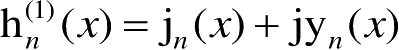 为第一类球汉开尔函数;
为第一类球汉开尔函数;
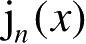 为第一类球贝塞尔函数;
为第一类球贝塞尔函数;
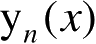 为第二类球贝塞尔函数。无量纲RCS是以球面积
为第二类球贝塞尔函数。无量纲RCS是以球面积
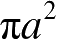 进行的归一化,表示为NRCS,又称为后向散射有效因子,其表达式为
进行的归一化,表示为NRCS,又称为后向散射有效因子,其表达式为
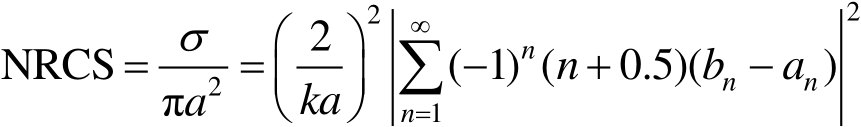
(2.112)
由式(2.112)精确计算NRCS随 ka 的变化情况, ka 值从0.02增到20,计算间距为0.02。图2.24(a)所示为瑞利区导电球的NRCS值,其 ka = 0~2,一般文献上没有给出这样精确的值。尤其对在 k a ≈1 附近的数据做标定非常有用。例如,从附录B数据中查得,第一个峰值处于 ka = 1.02,其相应NRCS最大值为3.6535。图2.24(b)可用于求谐振区导电球的NRCS值,其 ka = 0~20,它也比一般文献上给出的值精确。
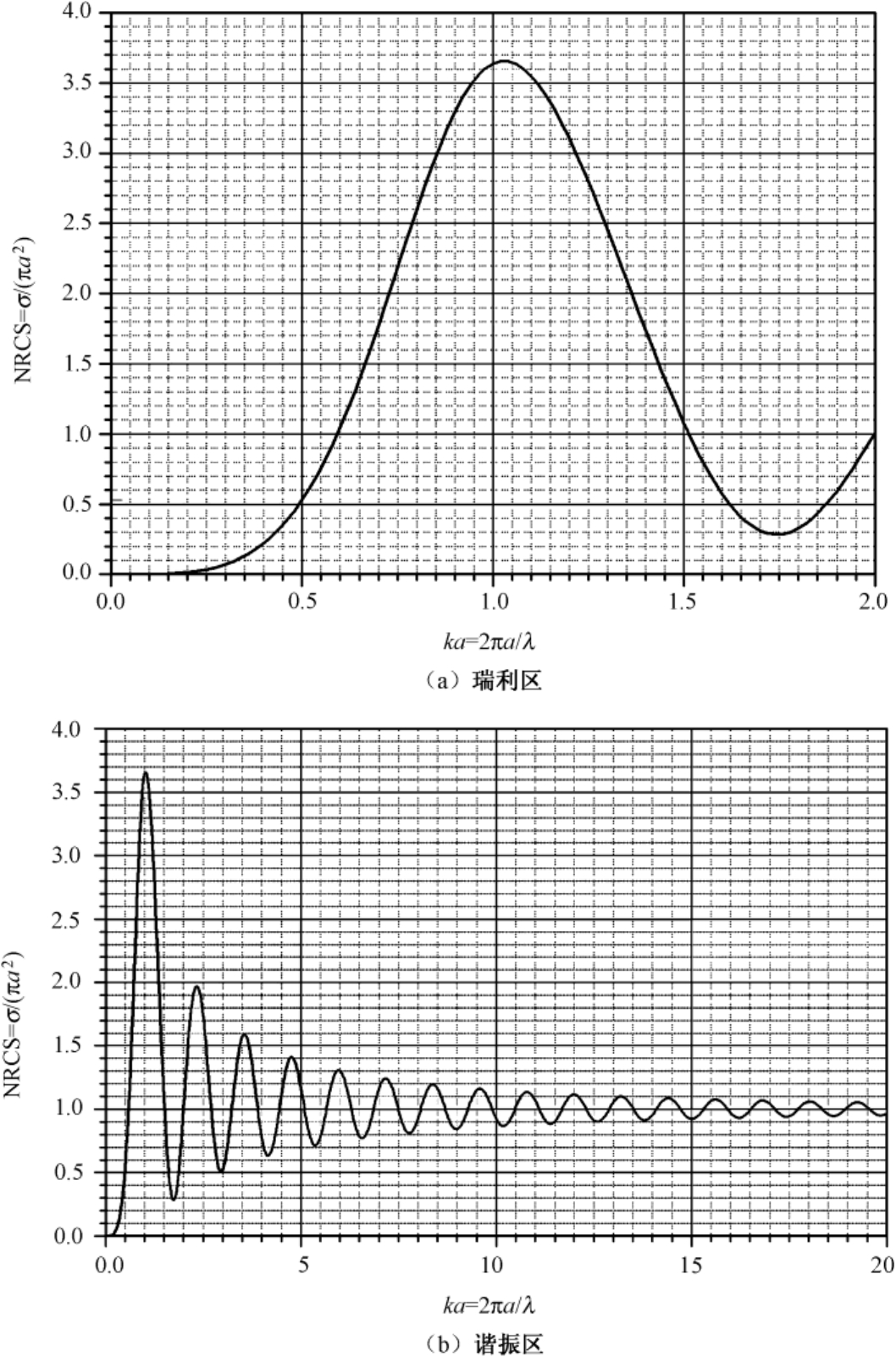
图2.24 导电球的NRCS值
导电球的相位信息也是相当有用的,在微波成像和识别、角闪烁等研究中都需要用到,而在一般文献中很少给出。图2.25给出了导电球相位随 ka 的变化曲线。
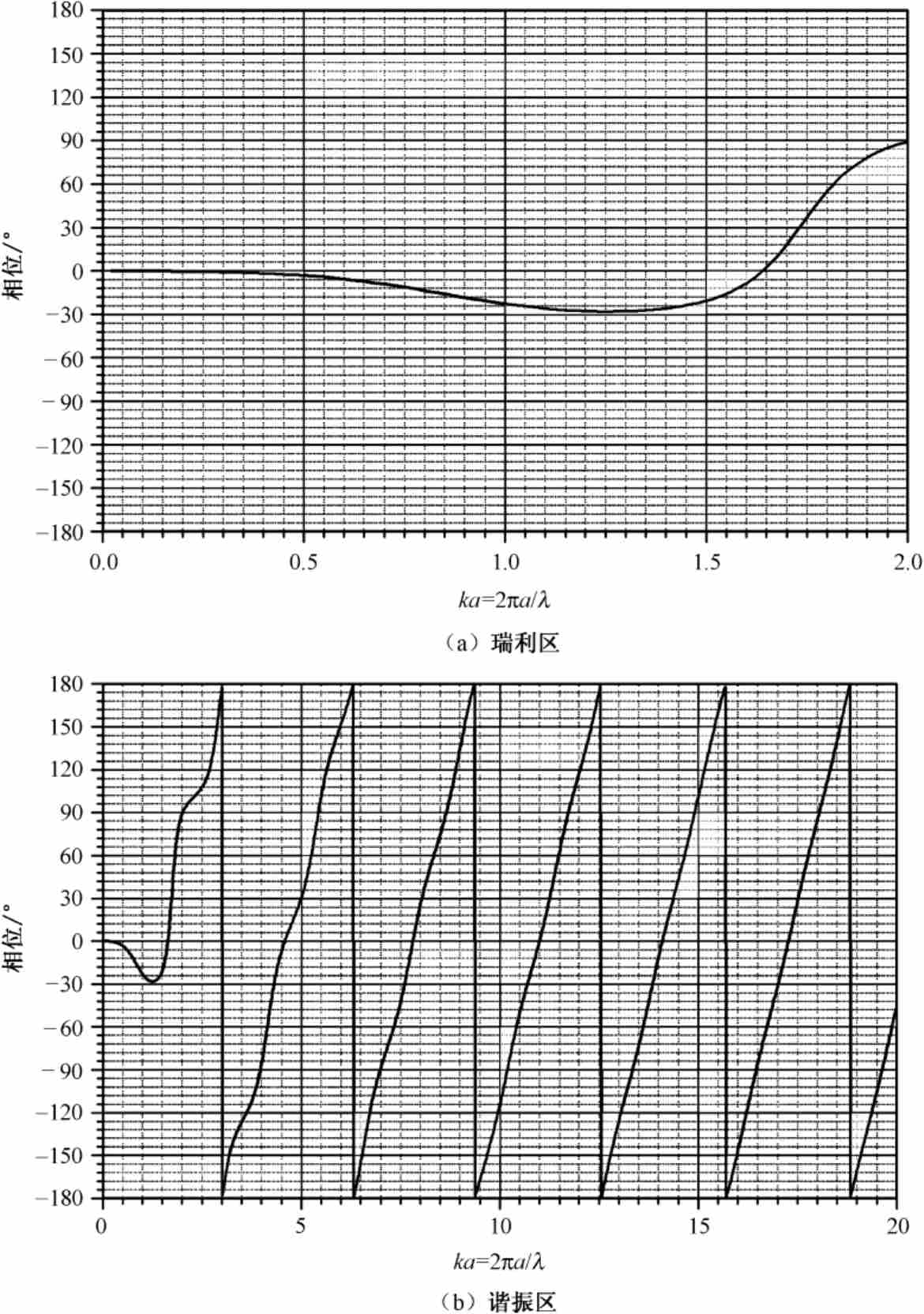
图2.25 导电球相位随 ka 的变化曲线
为了便于读者自行利用计算机数值求解金属球的后向RCS和相位,附录C给出了利用FORTRAN语言编写的计算机程序,有关的输入和输出量在程序注释中已说明。
在测量诸如舰船等大散射截面目标时,需要用角反射器或金属平板作为定标体。在相同尺度下,平板要比球的RCS大好几个数量级。在测平板雷达吸波材料反射率时,也需要以同样大小的金属平板为基准。金属平板定标体的主要缺点是散射方向图太窄,因此在实际测量中要用一台1.06μm波长的激光仪作为法向瞄准工具。
即使对有限尺寸的金属平板,其后向RCS也不易精确计算。这里仅考虑在 xOy 平面内入射的情况,如图2.26所示。下面给出了几种高频区金属平板后向RCS的计算公式 [94] ,其中,垂直(V)和水平极化(H)分别表示入射电场垂直和平行于 x Oy 平面。
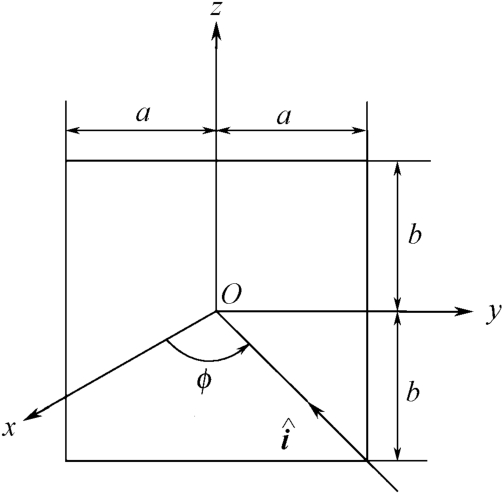
图2.26 金属平板的几何关系
(1)物理光学(PO)解,即
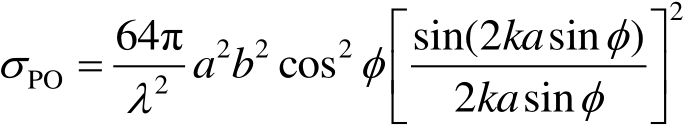
(2.113)
式(2.113)与极化无关。
(2)几何绕射理论(GTD)解,即
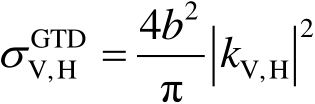
(2.114)
式(2.114)中,
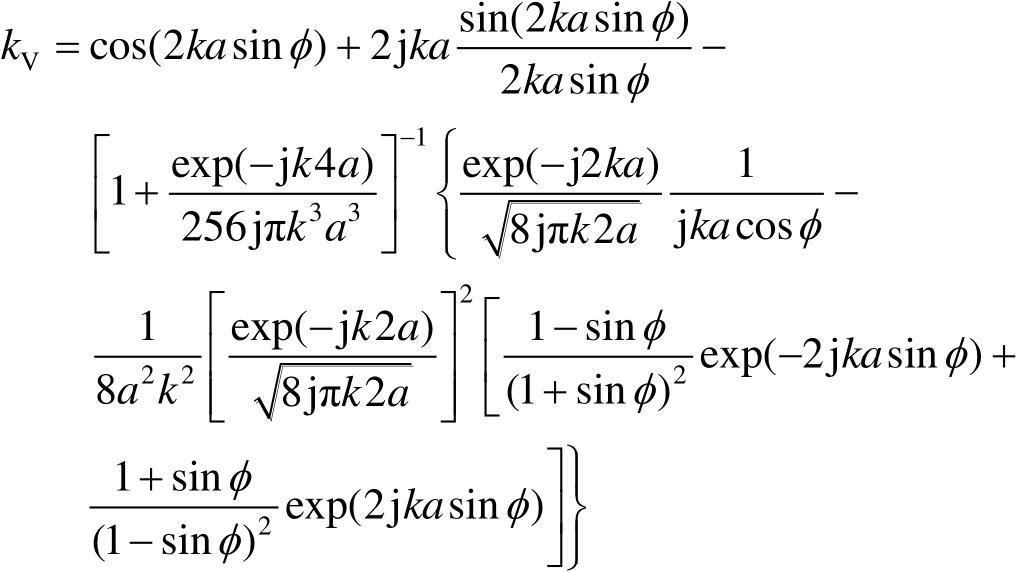
(2.115a)
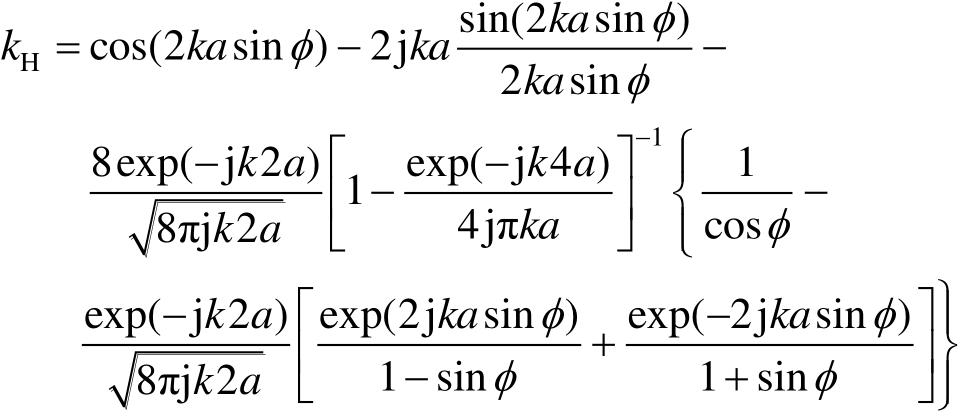
(2.115b)
(3)一致性渐近理论(UTD)解,其中:
垂直极化状态的RCS为
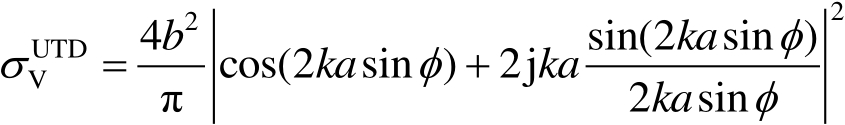
(2.116)
水平极化状态的RCS为
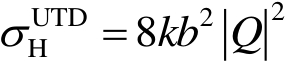
(2.117)
式(2.117)中,
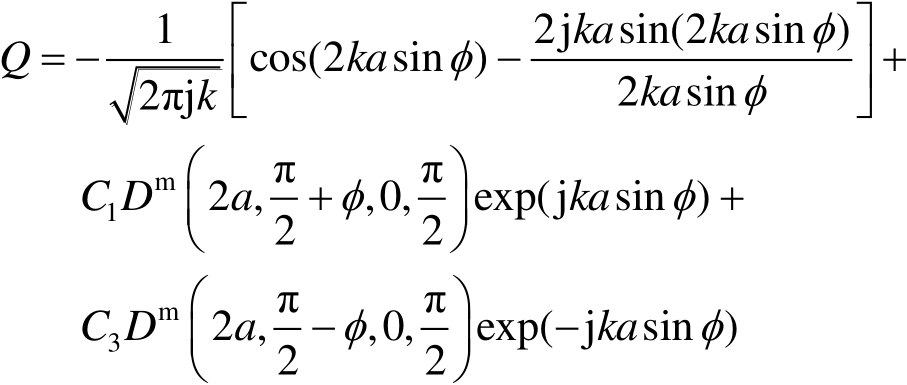
(2.118)
式中,
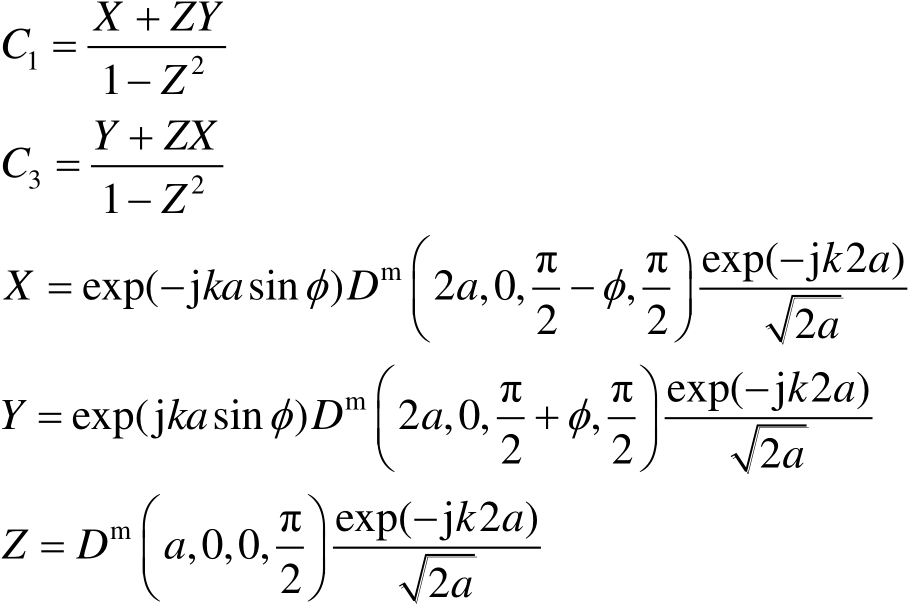
这里,
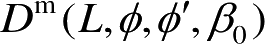 是半平面的硬边界绕射系数,可参见式(2.61),其中,
n
=2,
是半平面的硬边界绕射系数,可参见式(2.61),其中,
n
=2,
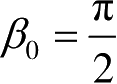 。
。
图2.27所示为利用物理光学法[见式(2.113)]计算的正方形金属平板的法向后向RCS随
ka
变化的曲线,其纵坐标RCS值用波长
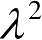 进行归一化,并取常用对数,因此单位为dB。
进行归一化,并取常用对数,因此单位为dB。
图2.28给出了两种极化状态下正方形金属平板后向RCS随入射角变化的曲线。纵坐标RCS用其相对于1m
2
的分贝数来表达,即分贝平方米(dBm
2
)。金属平板尺寸为30cm×30cm。实验数据由北京环境特性研究所的实验给出。在法向入射角20°范围内,PO解计算尚精确。超过这个入射角时,必须考虑金属平板前后面间的多次绕射。虽然用GTD和UTD都可以得到比PO法更好的结果,但在接近掠入射(
ϕ
=90°)时,GTD解是奇异的,因此建议用UTD来求解金属平板的RCS。可以注意到,当
 超过大约40°以后,理论解与测量值存在一定的差距,其原因在于实际金属平板是有厚度的,以及多次绕射的影响。特别是对水平极化的情况,后一影响更为显著。
超过大约40°以后,理论解与测量值存在一定的差距,其原因在于实际金属平板是有厚度的,以及多次绕射的影响。特别是对水平极化的情况,后一影响更为显著。
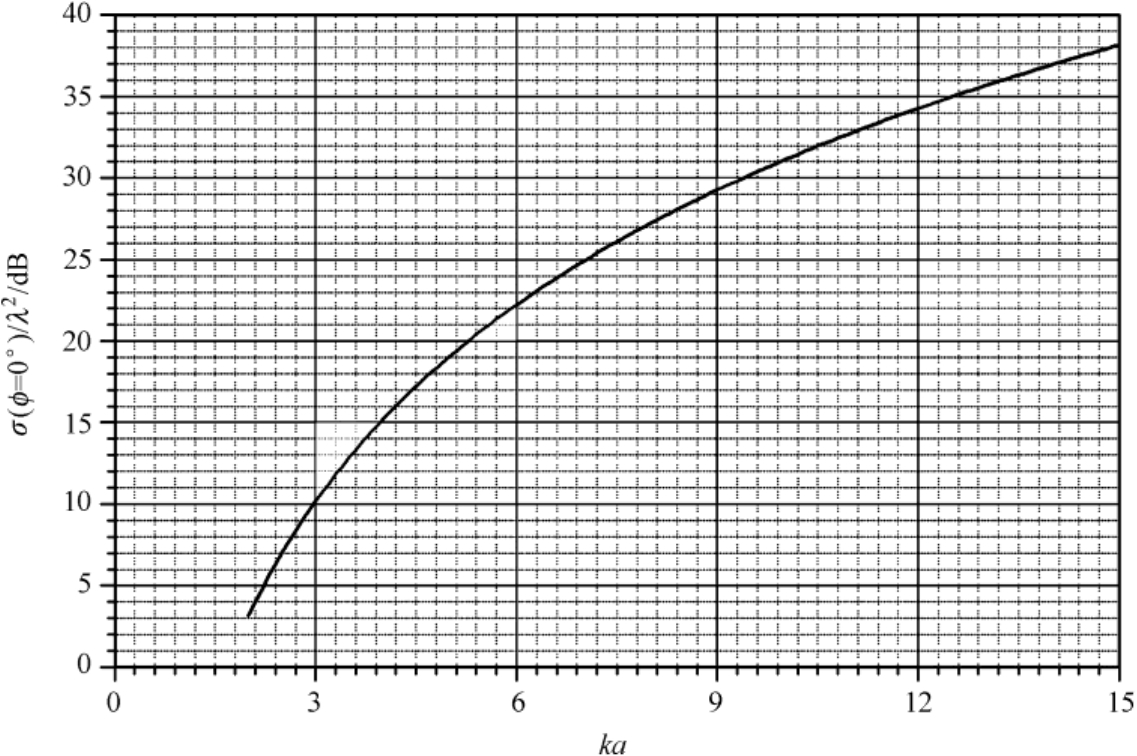
图2.27 正方形金属平板的法向后向RCS随 ka 的变化曲线
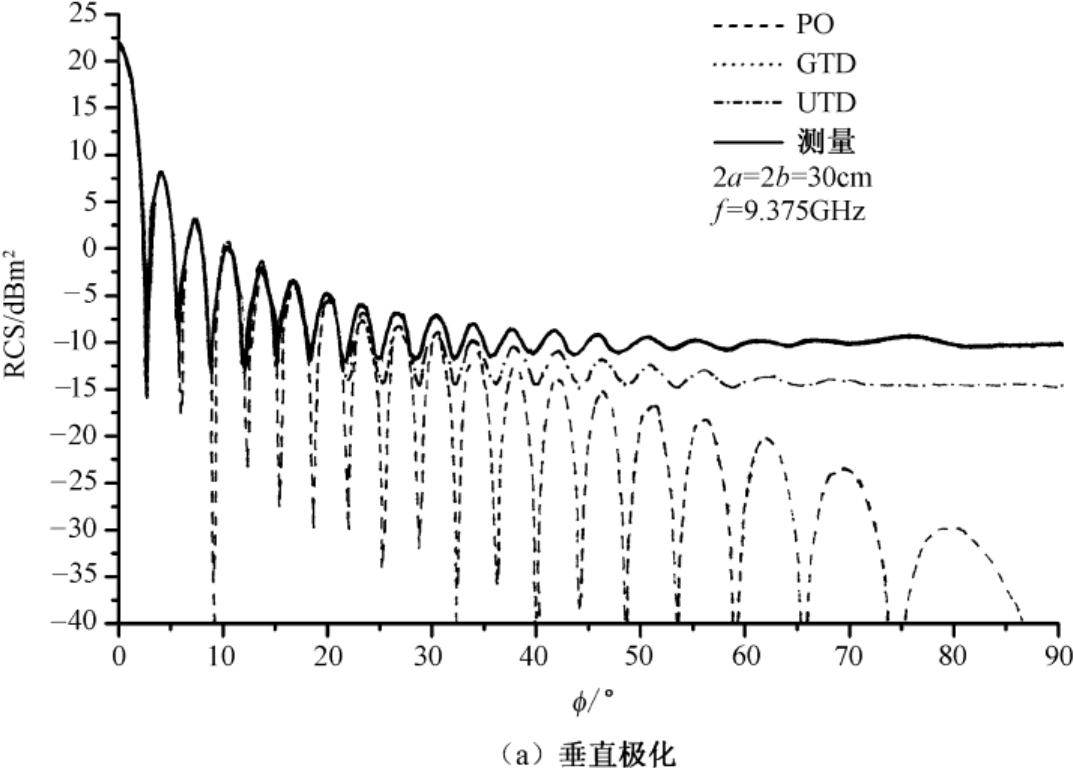
图2.28 正方形金属平板后向RCS随入射角变化的曲线
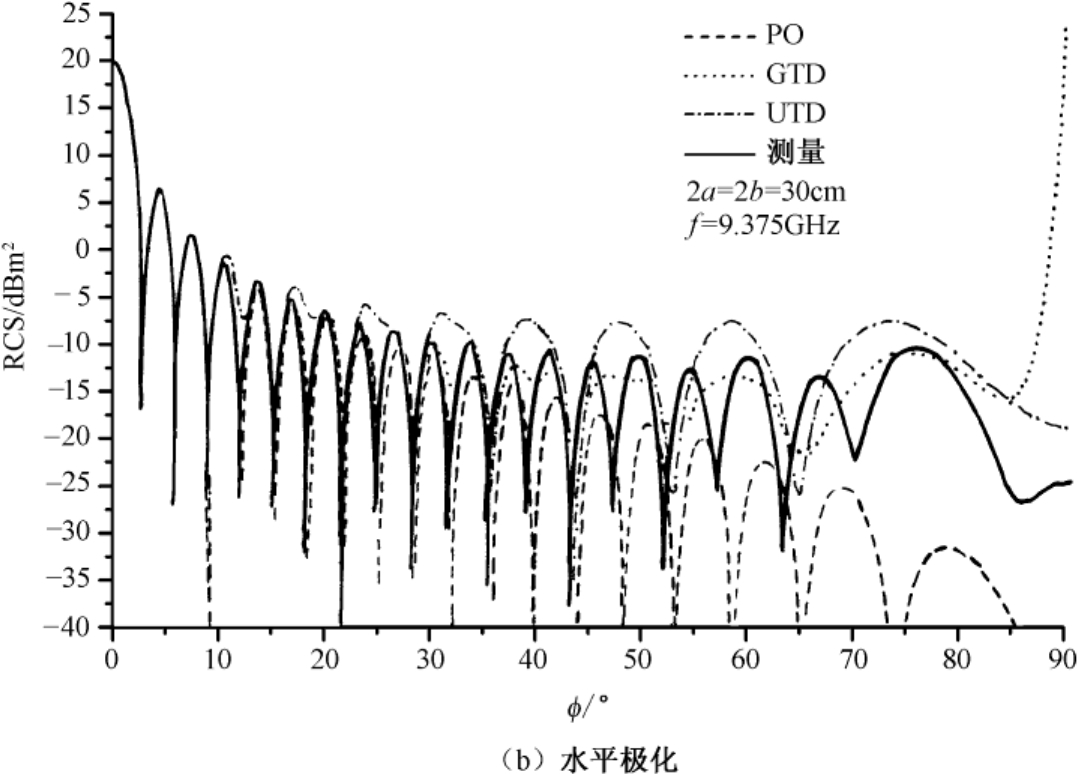
图2.28 正方形金属平板后向RCS随入射角变化的曲线(续)
本节介绍两类基于光学原理设计的可用于RCS标定的反射器,它们分别是各种二面、三面角反射器和龙伯(Luneberg)球透镜反射器,通过镜面反射、透射与聚集等作用将电磁波从来波方向原路反射回去,而且得到增强。
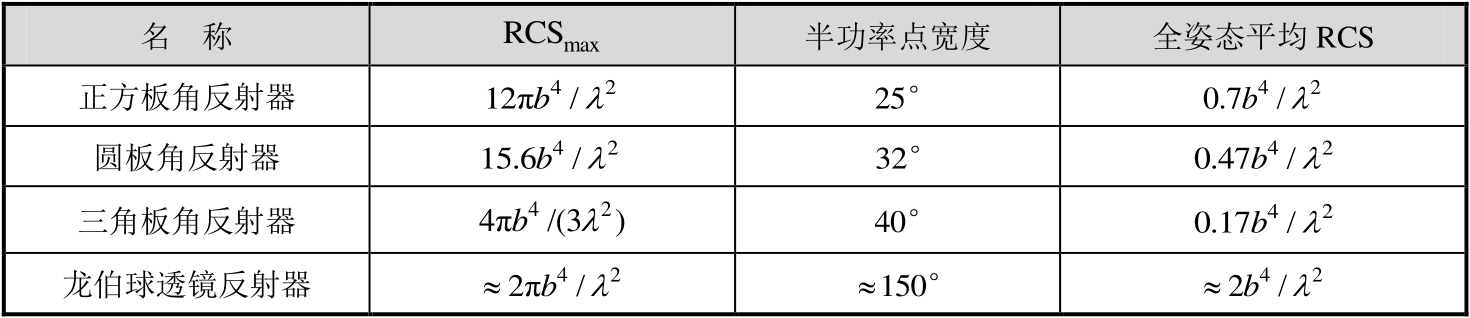
各种三面角反射器和龙伯球透镜反射器如图2.29所示,它们的RCS计算公式、半功率点宽度和全姿态角平均RCS参数均列于表2.11之中 [95] 。
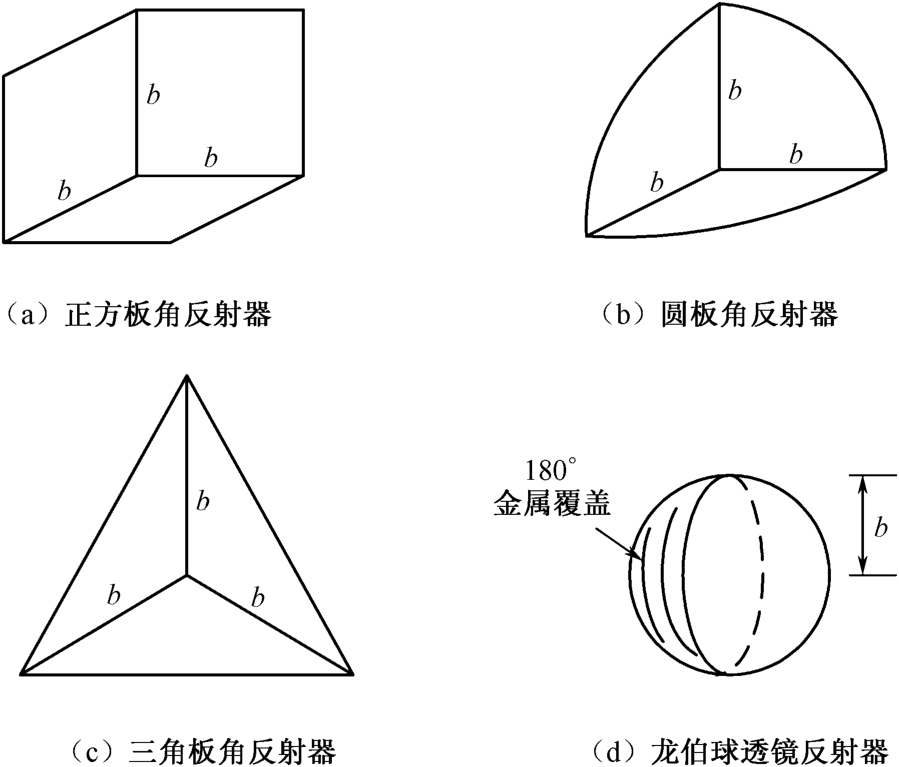
图2.29 各种三面角反射器和龙伯球透镜反射器
表2.11 各类反射器的RCS参数
RCS最大值也可由曲线查出,如图2.30所示。例如
λ
=0.1m,
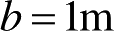 ,对正方板角反射器,由图中曲线查出
σ
=3800m
2
,该值与表2.11算出的
,对正方板角反射器,由图中曲线查出
σ
=3800m
2
,该值与表2.11算出的
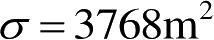 非常接近。如果采用圆板角反射器,则仅需将图2.30的
σ
乘以0.414。如果采用三角板角反射器,则需将图2.30的
非常接近。如果采用圆板角反射器,则仅需将图2.30的
σ
乘以0.414。如果采用三角板角反射器,则需将图2.30的
 数据乘以0.111。但该表不适用于
b
<
λ
的情况。
数据乘以0.111。但该表不适用于
b
<
λ
的情况。
角反射器的方向图可用极坐标系内栅格来衡量,如图2.31所示。图中 θ 角表示由 z 轴算起的俯仰角, ϕ 角表示垂直于 z 轴的 xy 平面上由 x 轴算起的方位角。栅格中的变参量为以出现在 θ ≈54.74° 和 ϕ ≈45° 处的最大RCS值做归一化后的方向图电平。
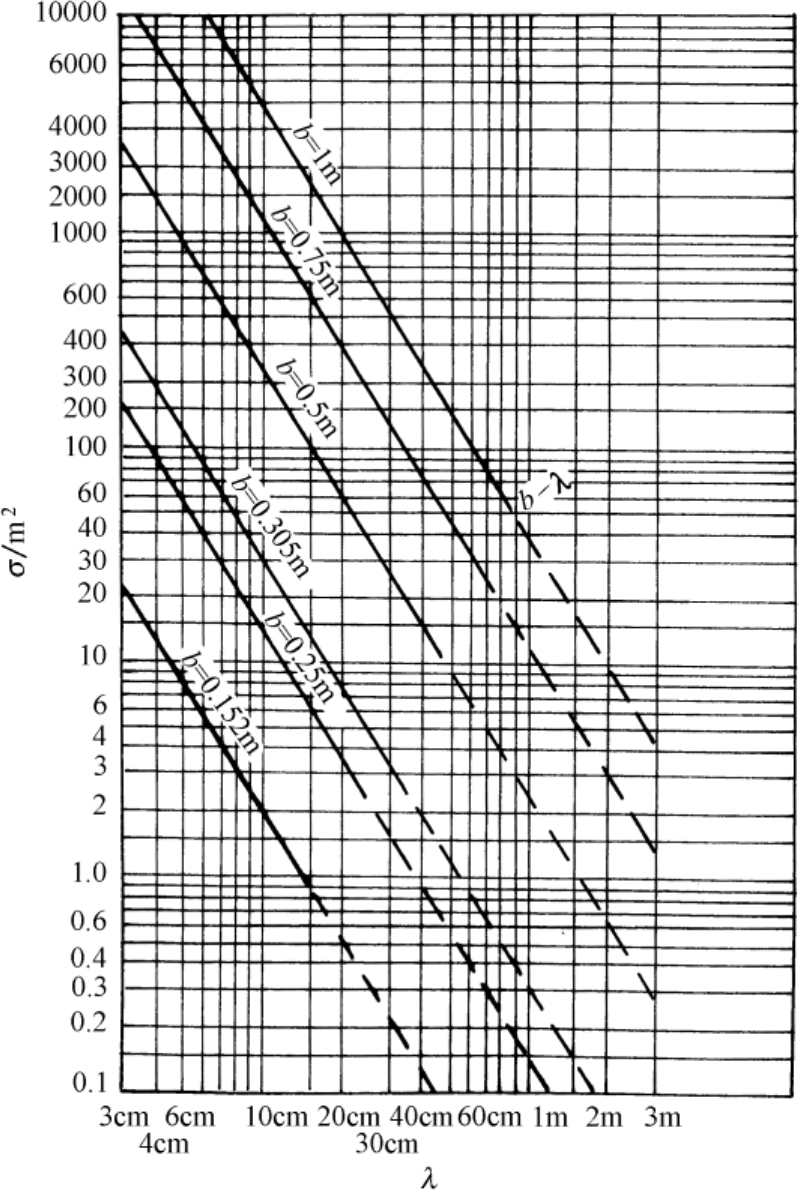
图2.30 正方板角反射器最大RCS曲线
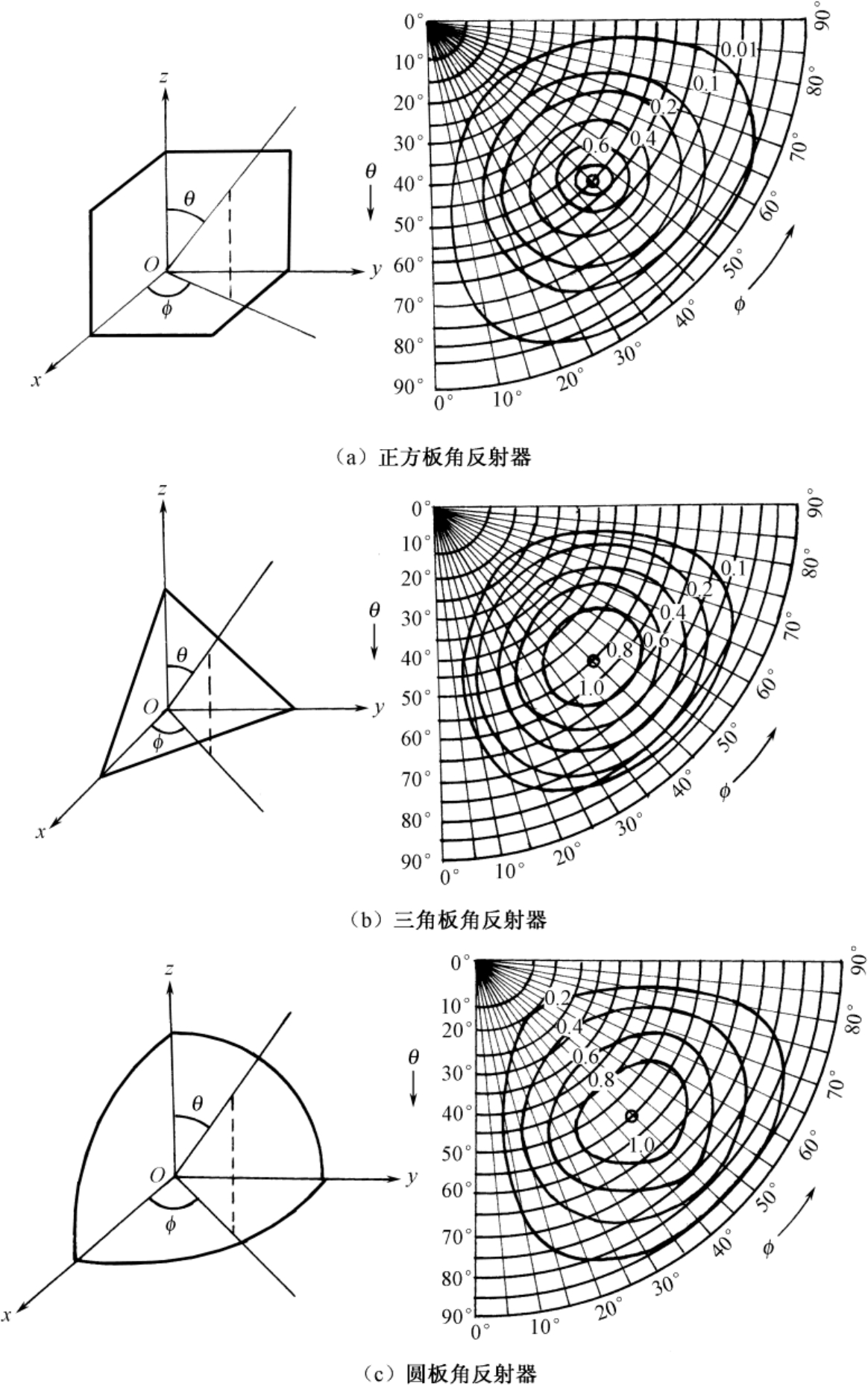
图2.31 角反射器的方向图曲线
图2.32以另一种形式给出了上述4种角反射器的最大后向RCS值随 b / λ 变化的曲线。
由于反射器加工制作时的误差,尤其三面体的相互垂直度不准确,因此实际反射器的RCS值略小于理论计算值,一般误差在1dB之内。图2.33给出了 b = 73.6cm的三角板角反射器在15.2GHz频率点两种极化的后向RCS测量结果(三角板角反射器的口径垂直于地面,其中,HH:尖头着地,VV:一条边着地)。有时为了获得更宽角度范围内的大RCS,需要将多个三角板角反射器进行适当组合。图2.34给出了三个 b = 73.6cm的三角板角反射器的一种排列组合方式,其中三角板角反射器沿圆弧排列,左右两个的中线偏离中心线都是20°。图2.35所示为该组合反射器在15.2GHz频率上的后向RCS的HH极化测量结果。
以上各类角反射器对极化是逆转180°的,因此当入射波为线极化时,回波与入射波具有同样方向;而当入射波为左旋圆极化波时,则回波为右旋圆极化波。由于一般飞行器也具有类似特性,因此通常单脉冲雷达抛物面天线也是这样设计的,即左旋发,右旋收。但当雷达指定用同一种圆极化发射接收时,则它将接收不到上述各角发射器的发射回波;如角反射器要满足入射波与反射波是同一圆极化波,则有两种形式 [95] :一种如图2.36所示,称为介质板角反射器,其相对频带宽度为±10%,按表2.11计算约有2dB误差;另一种为介质填充角反射器,如图2.37所示,介质的相对介电常数2.3≤ ε r ≤4.0,按表2.11计算有1.5dB误差,它具有与原来不填充介质的角反射器同样的频带宽度。
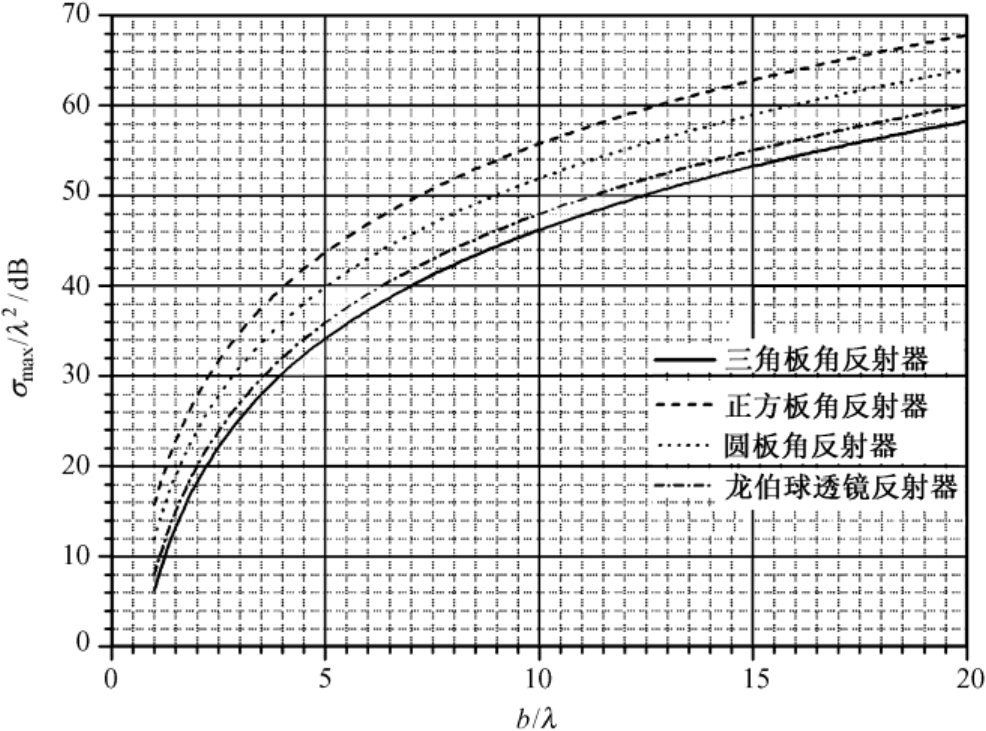
图2.32 4种角反射器的最大后向RCS值随 b / λ 变化的曲线

图2.33 三角板角反射器的后向RCS测量结果
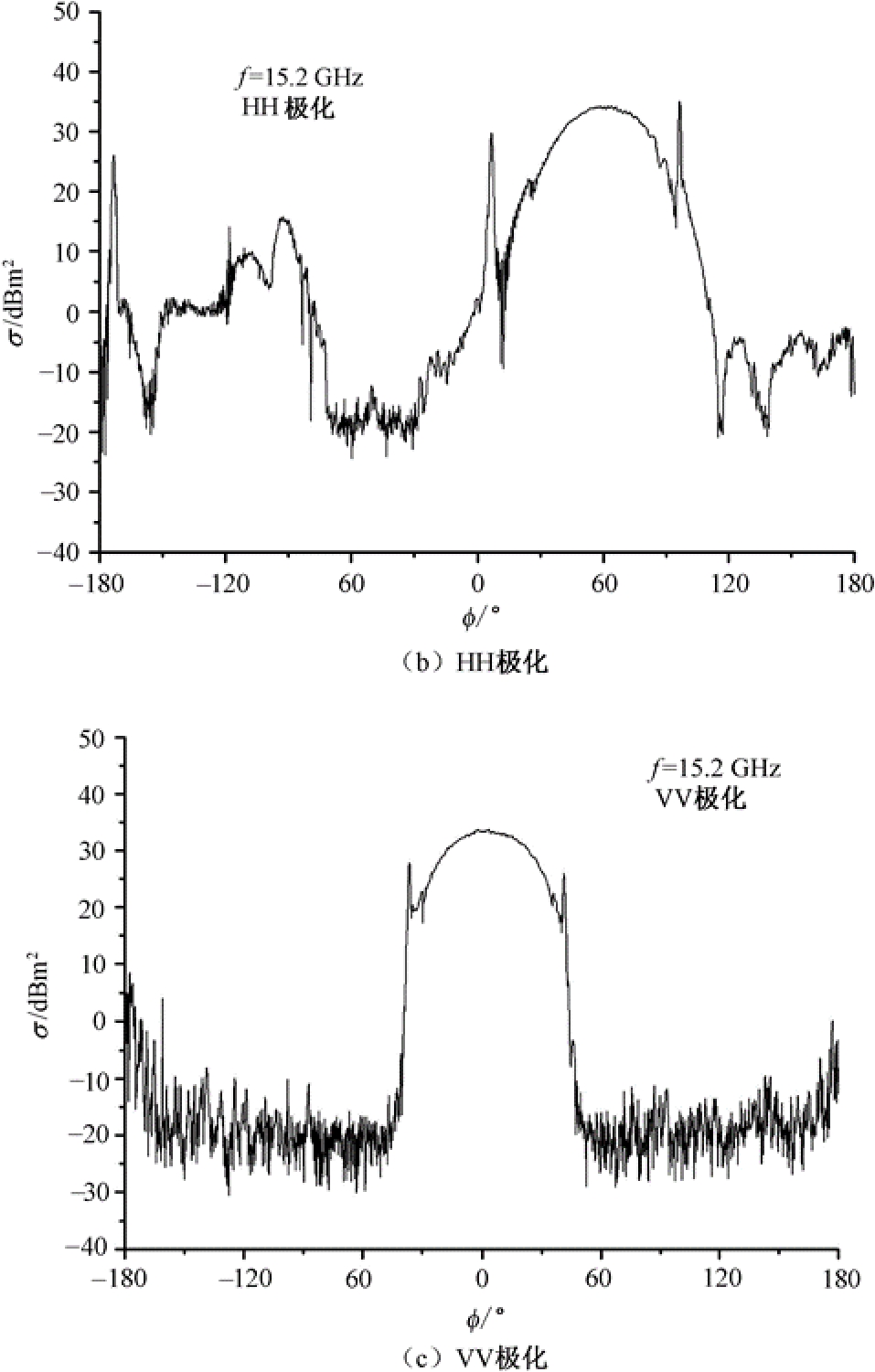
图2.33 三角板角反射器的后向RCS测量结果(续)

图2.34 三个三角板角反射器的组合
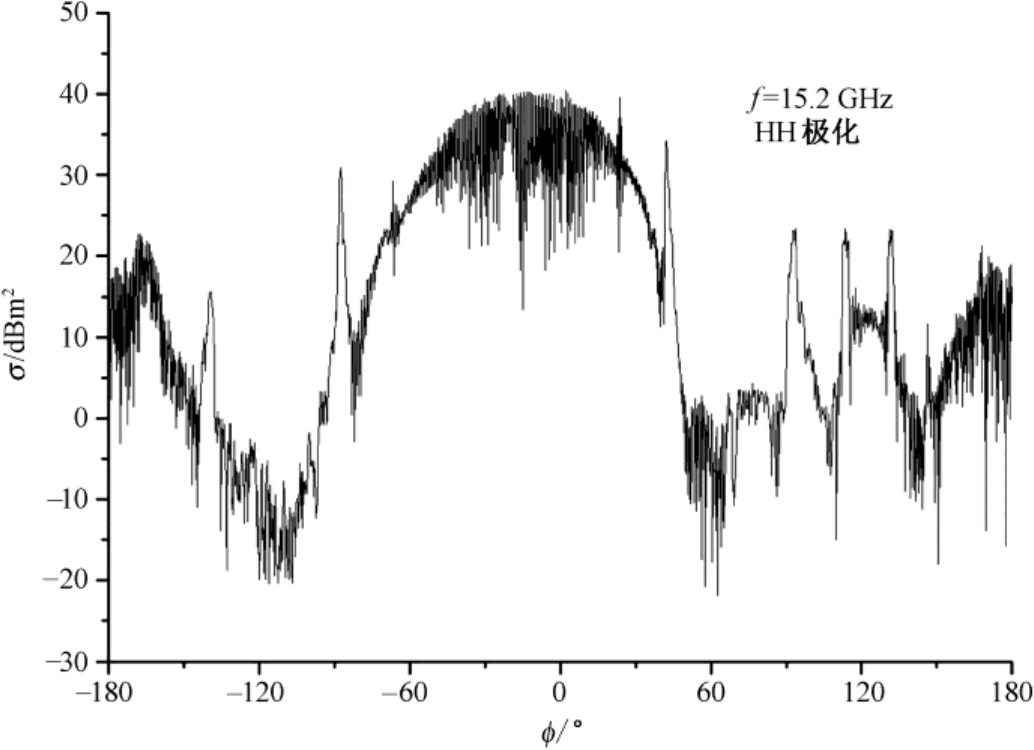
图2.35 三个三角板角反射器后向RCS的HH极化测量结果
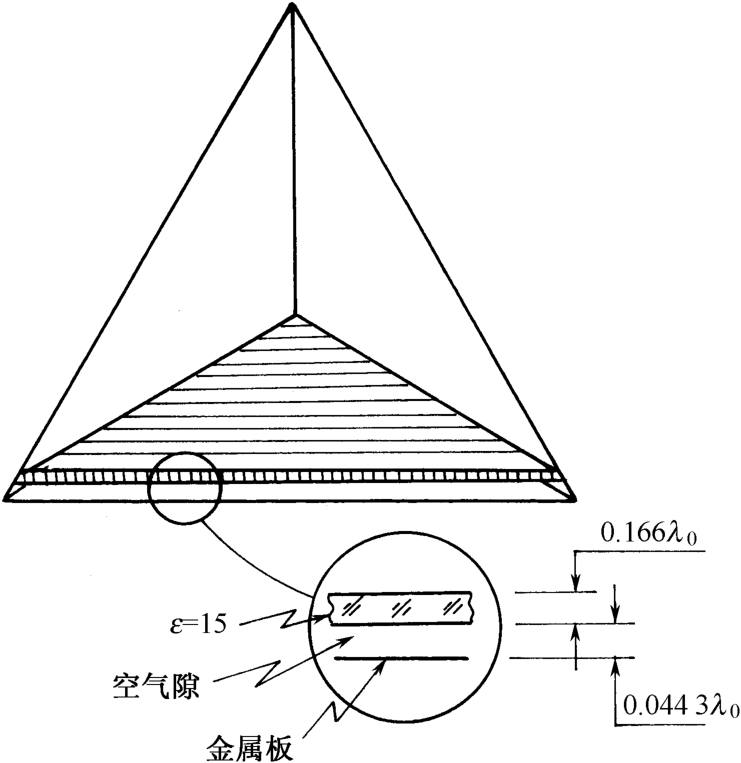
图2.36 介质板角反射器
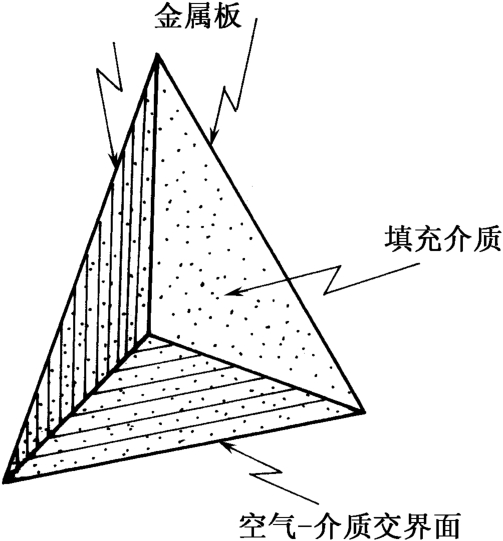
图2.37 介质填充角反射器
当在三角板角反射器的一个内表面上按规定的尺寸和取向加上金属片或矩形槽纹时,如图2.38所示,对于垂直和平行场分量相等的线极化入射波,它可以提供圆极化或90°扭转极化的反射波。图2.39给出了在 θ ≈54.74° 和 ϕ ≈45° 的视线上产生90°扭转极化和圆极化反射波的金属片或矩形槽纹的设计曲线。关于这种角反射器更详细的讨论可参见文献[96]。
由两块矩形板正交形成的金属二面角反射器也可用于RCS的标定,如图2.40所示。用做定标体的二面角反射器的宽度
w
一般要求不小于5
λ
[97]
。与三角板角反射器类似,二面角反射器的散射方向图在一个主平面(方位面)上是宽的,但在另外一个主平面(俯仰面)却表现出与矩形平板类似的
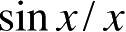 的散射特性。尽管后一种散射特性是人们所不希望出现的,但二面角反射器具有三角板角反射器所没有的一种有用特性:通过适当取向,二面角反射器是一种强的交叉极化回波源。当将二面角旋转45°时,它既可用于同极化RCS的标定,也可用于交叉极化RCS的标定,这一点将在7.2.2节说明。
的散射特性。尽管后一种散射特性是人们所不希望出现的,但二面角反射器具有三角板角反射器所没有的一种有用特性:通过适当取向,二面角反射器是一种强的交叉极化回波源。当将二面角旋转45°时,它既可用于同极化RCS的标定,也可用于交叉极化RCS的标定,这一点将在7.2.2节说明。
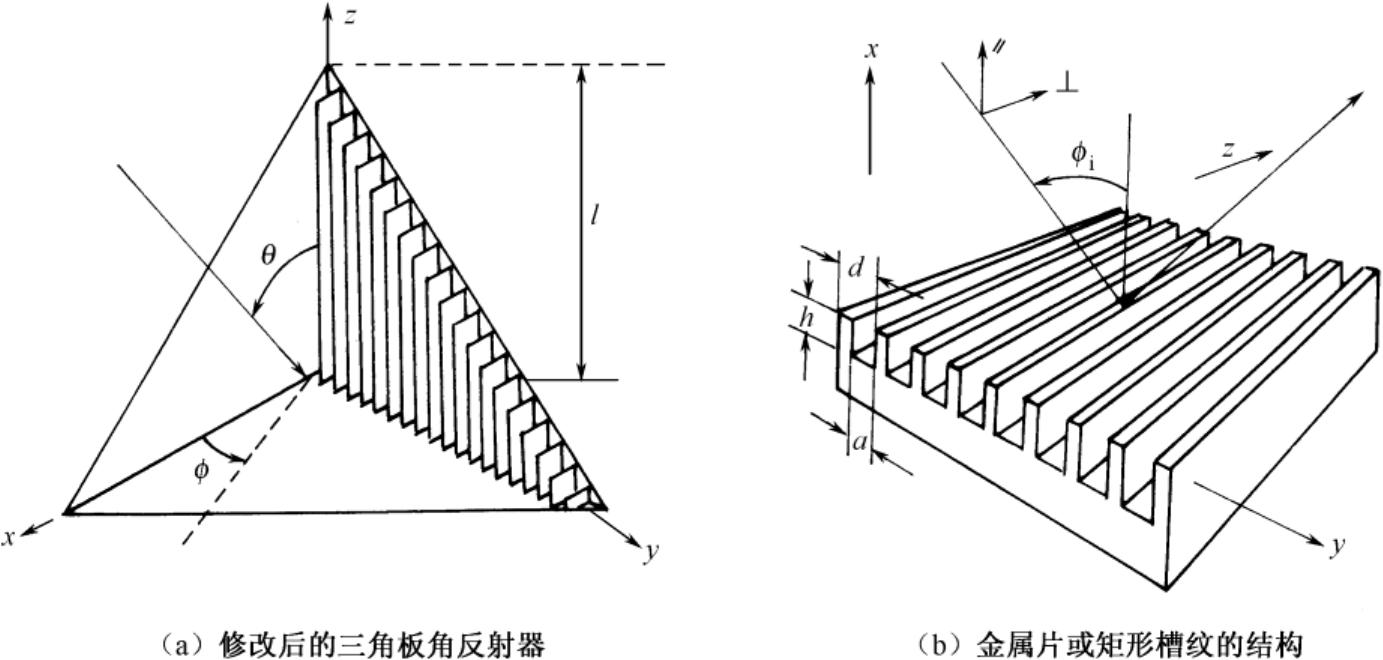
图2.38 内表面加有金属片或矩形槽纹的三角板角反射器
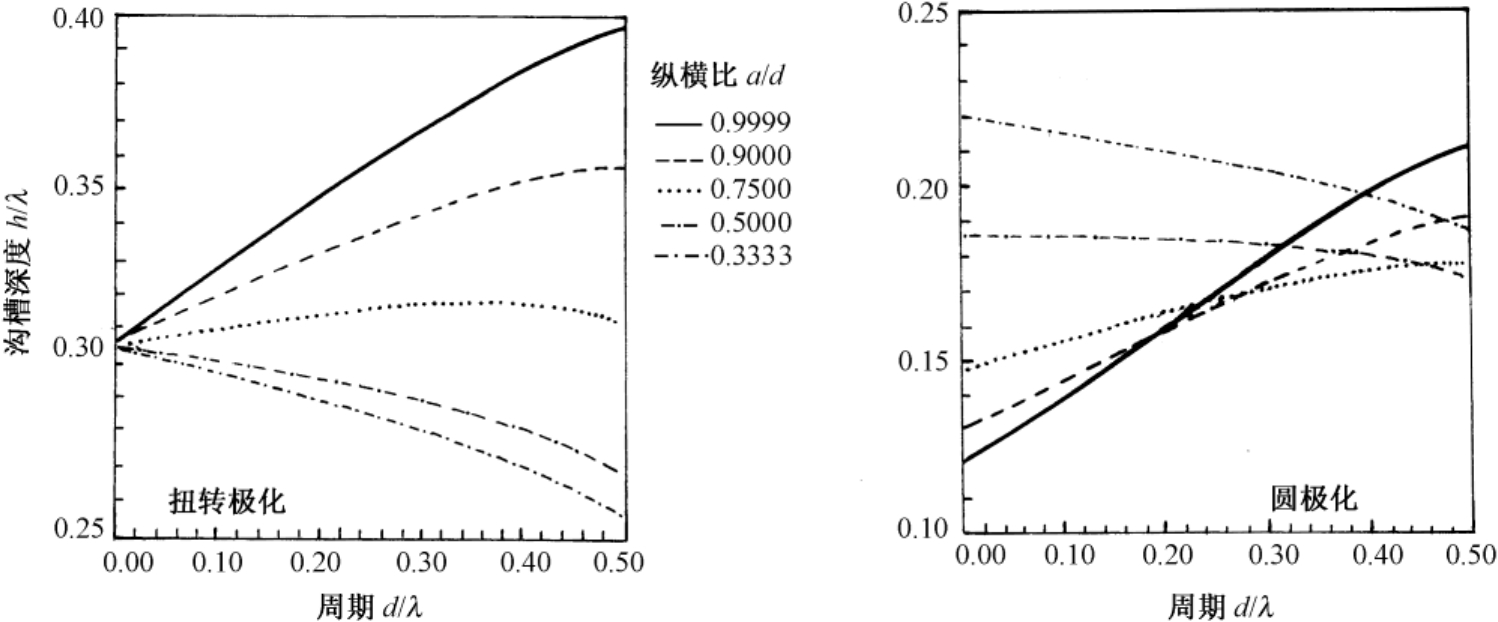
图2.39 产生90°扭转极化和圆极化反射波的金属片或矩形槽纹的设计曲线
直角二面角反射器的最大后向RCS为
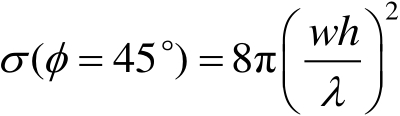
(2.119)
图2.41给出了不同 h / λ 值时二面角反射器的最大后向RCS随 w / λ 变化的曲线。
在双基地雷达状态下使用时,为了加宽角反射器的方向图宽度,可以设计成非直角状的角反射器,其计算方法可参照文献[98]第4章中非正交两面角反射器的有关推导。
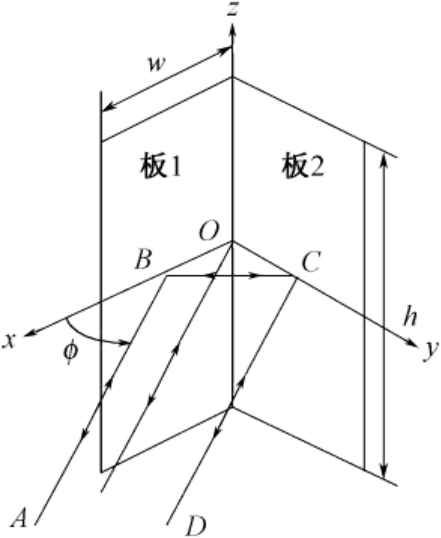
图2.40 金属二面角反射器
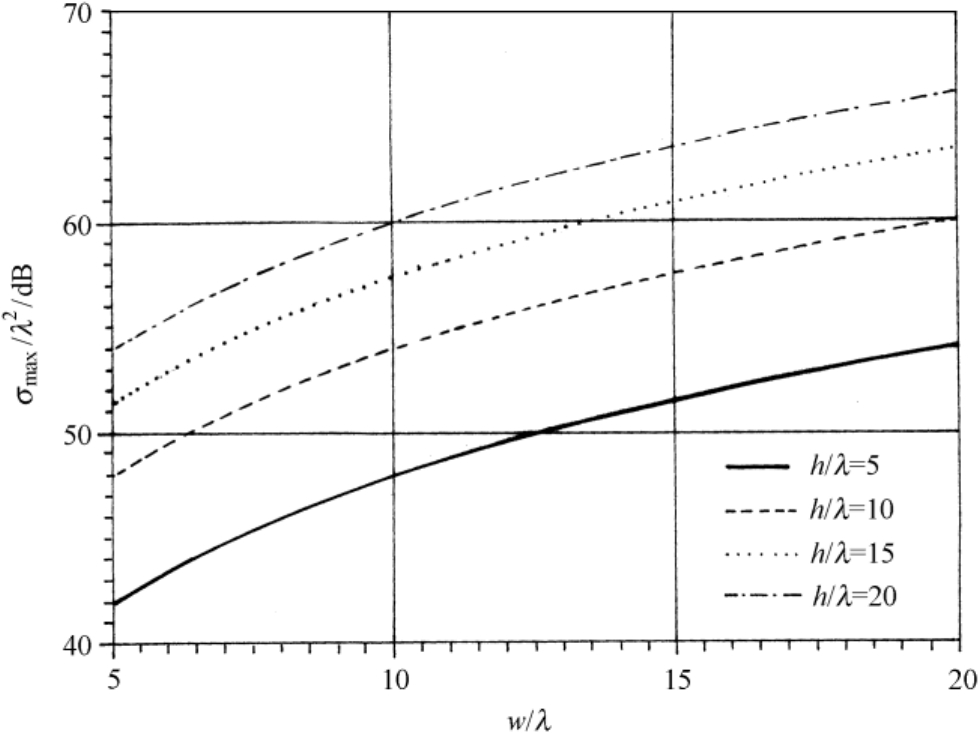
图2.41 不同 h / λ 时二面角反射器的最大后向RCS随 w / λ 变化的曲线
对于采用低散射金属支架的RCS测试场,传统的金属球定标体安装到支架上时,会与低散射支架产生很强的耦合散射,无法完成RCS的精确标定测量。因此,目前国际上普遍采用短粗圆柱体作为RCS定标体 [99 -100] ,多数实验室采用了高度与直径之比为7/15(0.4667)的一组金属圆柱体,其尺寸参数列于表2.12。在高频区,对圆柱体光滑平整的底部同低散射金属支架之间的耦合散射效应可以忽略不计。图2.42所示为直立的短粗金属圆柱定标体的几何外形,以及在低散射支架上的安装示意图。
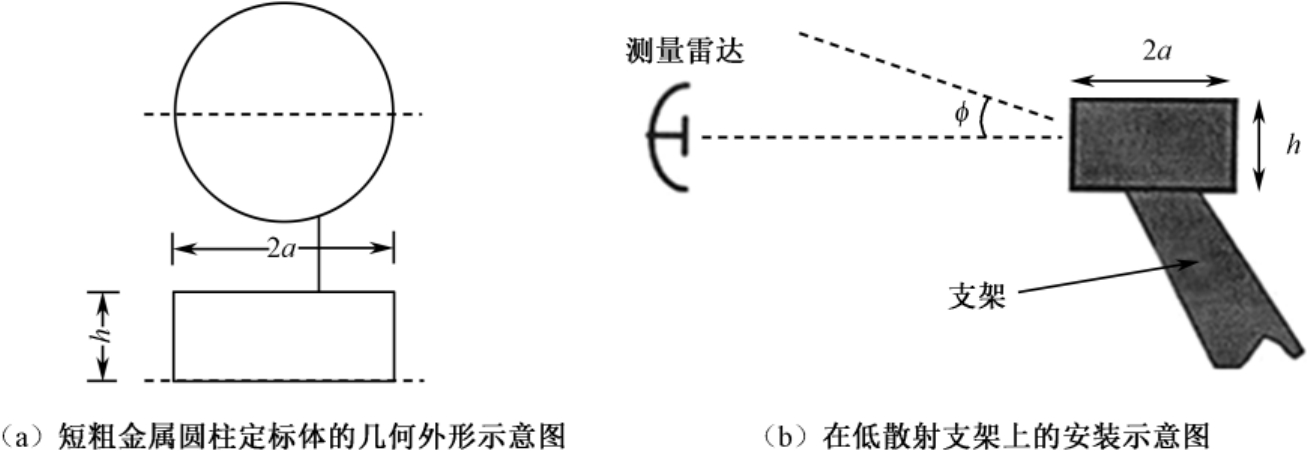
图2.42 金属圆柱定标体的几何外形及其在低散射支架上的安装示意图
与金属球的散射场具有精确Mie级数解析解不同,对于金属圆柱体,仅当圆柱为无限长时其散射场才有解析解。国际和国内学者已对这样一组金属圆柱体的精确RCS计算和测量进行了广泛的研究 [99-102] 。研究表明,为了得到短粗圆柱体RCS的幅度和相位的精确值,一般应采用矩量法(MoM)进行数值计算。
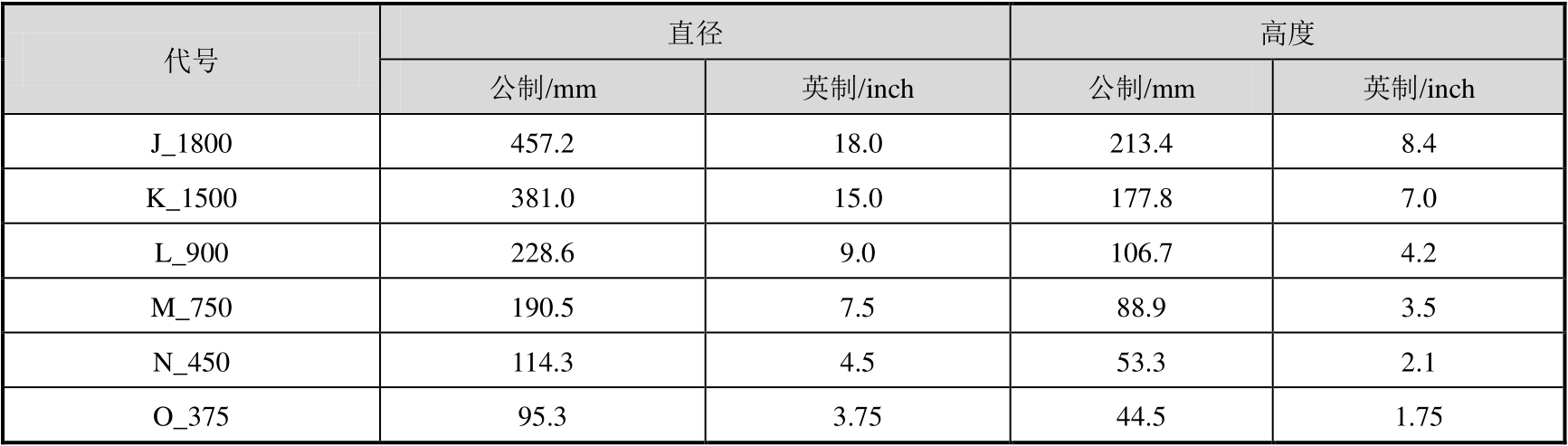
表2.12 目前国际上广泛采用的一组短粗金属圆柱定标体参数
直立金属圆柱体的物理光学近似计算公式为
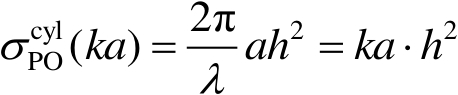
(2.120)
式(2.120)中,
a
和
h
分别为圆柱体的半径和高度;
λ
=
c
/
f
为雷达波长,
 为雷达频率,
c
为传播速度;
为雷达频率,
c
为传播速度;
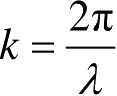 为空间波数。
为空间波数。
但是,仅当
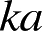 值足够大时,采用物理光学公式计算才足够精确。很多情况下,物理光学公式的计算精度并不足以用于RCS的标定。对短粗圆柱体的RCS精确计算,基本上都是采用基于矩量法的不同RCS计算代码。北京航空航天大学基于矩量法对标准圆柱体的RCS进行了精确数值计算,并基于短粗圆柱体的散射机理,结合数值计算数据,发明了一套可用于不同尺寸的标准圆柱定标体的精确RCS计算的参数化模型方法
[101]
。该方法已获得国家发明专利,其软件代码也已由北京航空航天大学遥感特征实验室公开,并列于本书附录D,可供采用高度与直径之比为7/15的短粗圆柱体作为定标体的各种RCS测试场使用。
值足够大时,采用物理光学公式计算才足够精确。很多情况下,物理光学公式的计算精度并不足以用于RCS的标定。对短粗圆柱体的RCS精确计算,基本上都是采用基于矩量法的不同RCS计算代码。北京航空航天大学基于矩量法对标准圆柱体的RCS进行了精确数值计算,并基于短粗圆柱体的散射机理,结合数值计算数据,发明了一套可用于不同尺寸的标准圆柱定标体的精确RCS计算的参数化模型方法
[101]
。该方法已获得国家发明专利,其软件代码也已由北京航空航天大学遥感特征实验室公开,并列于本书附录D,可供采用高度与直径之比为7/15的短粗圆柱体作为定标体的各种RCS测试场使用。
1. 圆柱定标体的电磁散射机理分析
在RCS的标定中,圆柱体一般直立安装在低散射支架上,圆柱体的平整面朝向上下,圆弧面垂直指向雷达视线。
为了分析短粗圆柱定标体的电磁散射机理,采用矩量法计算得到圆柱体的超宽带RCS的幅度和相位数据,并对数据进行时频分析。研究发现,短粗圆柱定标体的主要散射机理包括两种:一种是镜面反射分量(PO散射分量),另一种是表面波(包括行波与爬行波)分量。图2.43和图2.44所示分别为VV和HH极化下短粗圆柱定标体电磁散射机理 [100] 。图中标示为1~6的各种不同散射机理,详细列于表2.13,表中 d =2 a 为圆柱体直径。
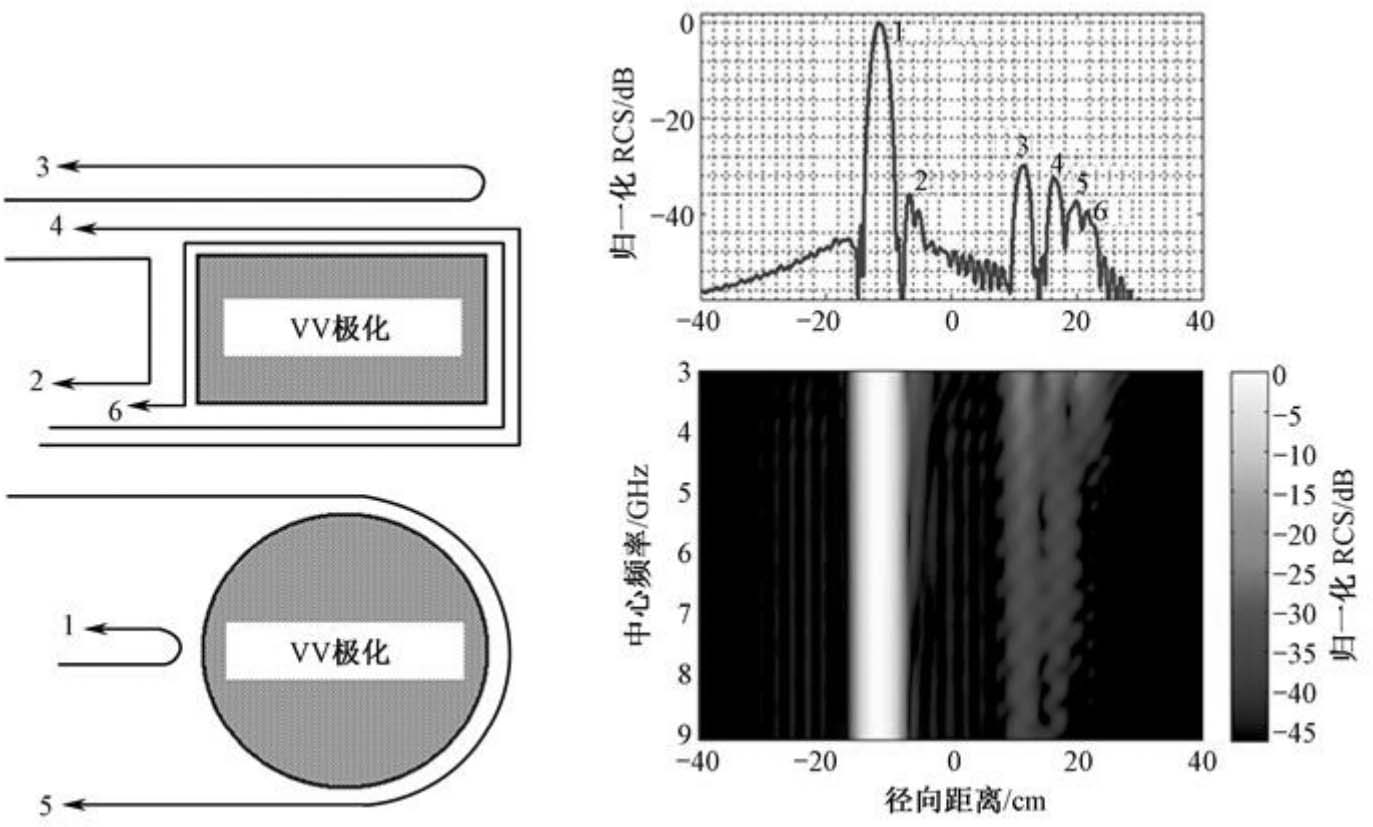
图2.43 短粗圆柱定标体的电磁散射机理,VV极化
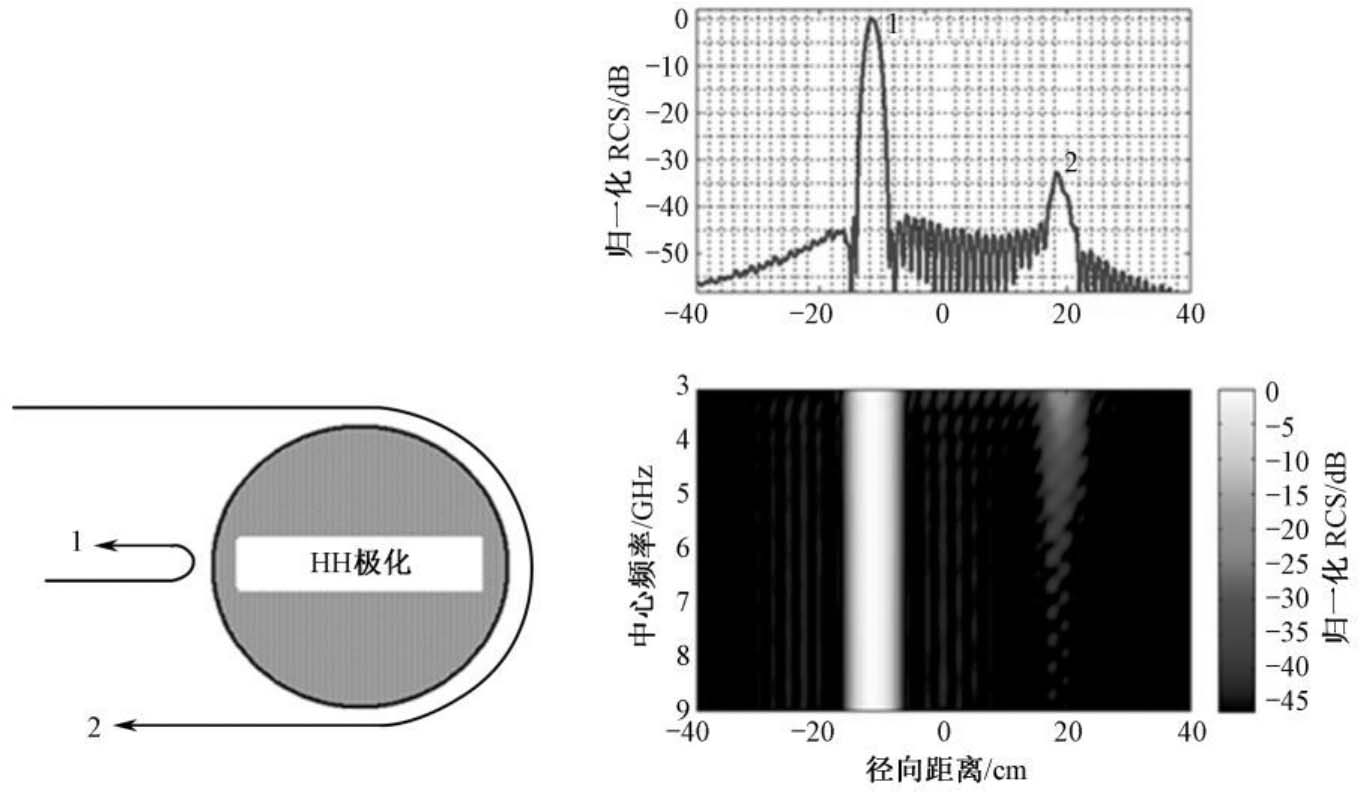
图2.44 短粗圆柱定标体的电磁散射机理,HH极化
图2.43和图2.44的右侧图分别为对直径9inch(228.6mm)的圆柱体宽带散射MoM计算数据进行时频分析的结果。根据电磁散射理论,当电磁波入射到金属表面时,仅当入射电场存在平行于或垂直于入射平面的电场分量时才会激发表面波 [103] ,其中入射平面定义为表面法线与入射线共同构成的平面。因此,如表2.13所示,对于VV极化,因在直立圆柱的圆弧面和上、下表面均满足激发表面波的条件,故其后向散射至少存在5个不同的表面波分量;而对于HH极化,则由于仅在柱面的圆弧面上激发出表面爬行波,上、下表面不会激发表面波,其主要散射机理只有两种。VV极化和HH极化下的这些散射机理在时频分析图中可以清晰地显示出来。同时,由于表面波散射电平随着雷达频率的升高而快速下降,使得短粗圆柱体在高频区成为一种优良的RCS定标体。
表2.13 不同极化下短粗圆柱定标体的主要散射机理
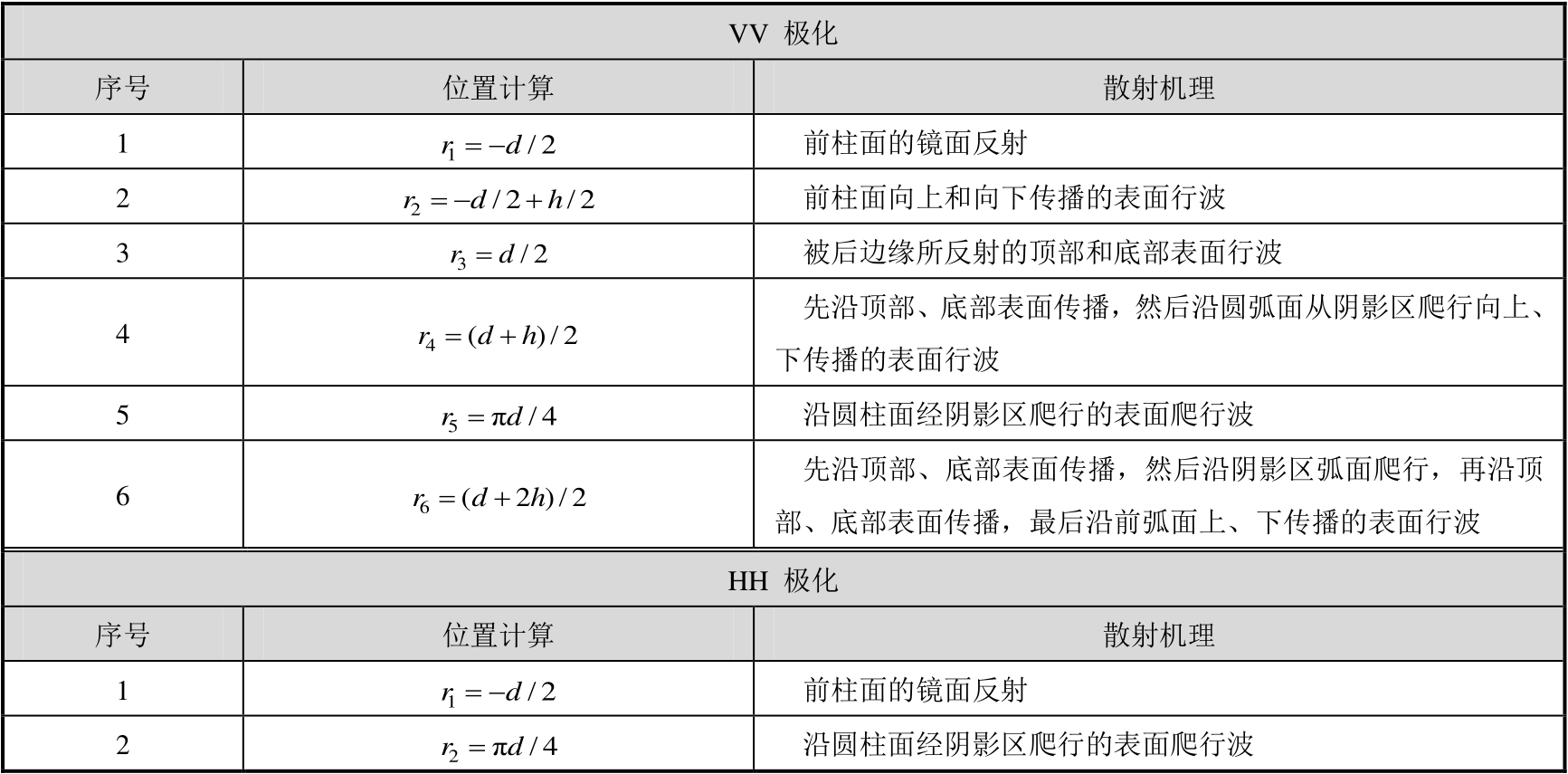
图2.45所示为直径228.6mm圆柱体的RCS幅度和相位随频率变化特性的计算结果。该图中,实线表示VV极化,虚线表示HH极化,点划线则表示经物理光学法高频近似的计算结果。
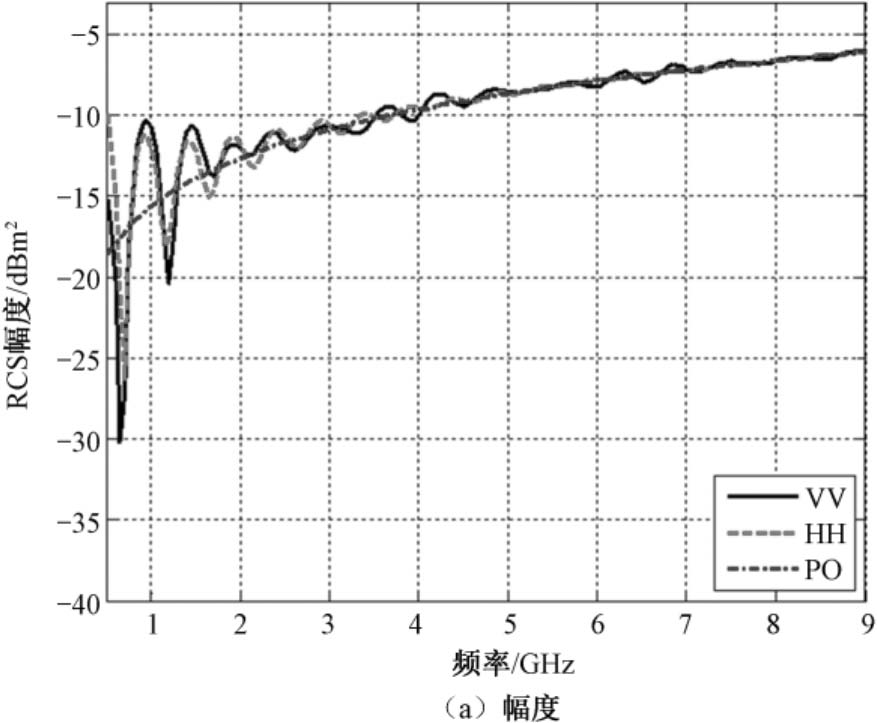
图2.45 直径228.6mm圆柱体的RCS幅度和相位随频率变化特性的计算结果
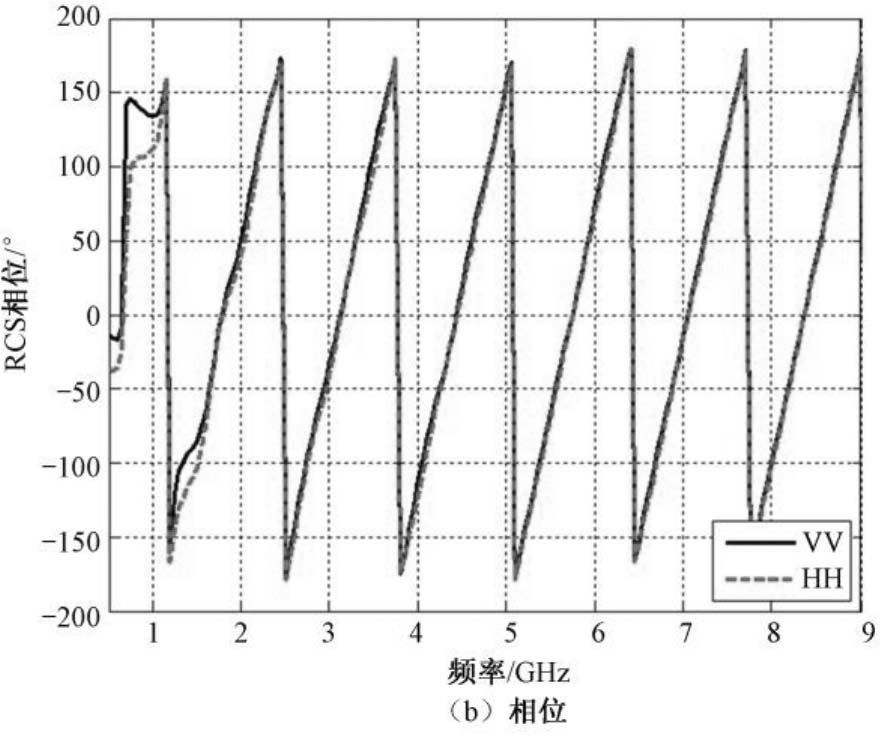
图2.45 直径228.6mm圆柱体的RCS幅度和相位随频率变化特性的计算结果(续)
用PO散射分量归一化的圆柱散射场随频率的变化特性可表示为
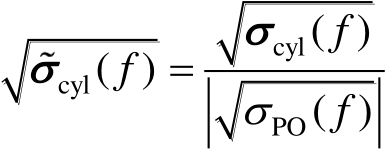
(2.121)
式(2.121)中,
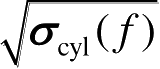 为圆柱定标体的散射函数;
为圆柱定标体的散射函数;
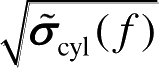 为经PO散射分量归一化后的散射函数;
为经PO散射分量归一化后的散射函数;
 表示圆柱定标体的PO散射分量。
表示圆柱定标体的PO散射分量。
式(2.121)中若将频率变量用
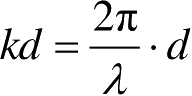 代替,则有
代替,则有
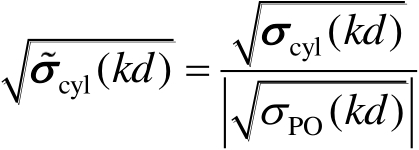
(2.122)
式(2.122)中,
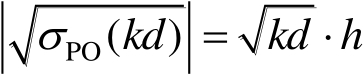
(2.123)
直径分别为228.6mm和114.3mm的金属圆柱定标体的归一化散射函数随频率的变化特性如图2.46所示。从图中可以发现,除了频率轴具有2倍缩比关系,经PO散射分量归一化后,两者的所有其他变化特性都是完全一样的。其中,对于228.6mm的圆柱体,频率范围为0.5~9GHz;而对于114.3mm的圆柱体,频率范围则为1~18GHz,正好是前者的2倍。
由此可见,对于任何尺寸的圆柱体,只要其高度与直径比保持为7/15或者其他常数,若以
k
d
值作为横坐标参变量,则经PO散射分量归一化后的散射函数
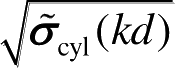 是不随圆柱体缩比尺寸变化的。也就是说,对于任何
k
d
值,标准圆柱定标体的归一化散射函数是确定的、唯一的。
是不随圆柱体缩比尺寸变化的。也就是说,对于任何
k
d
值,标准圆柱定标体的归一化散射函数是确定的、唯一的。
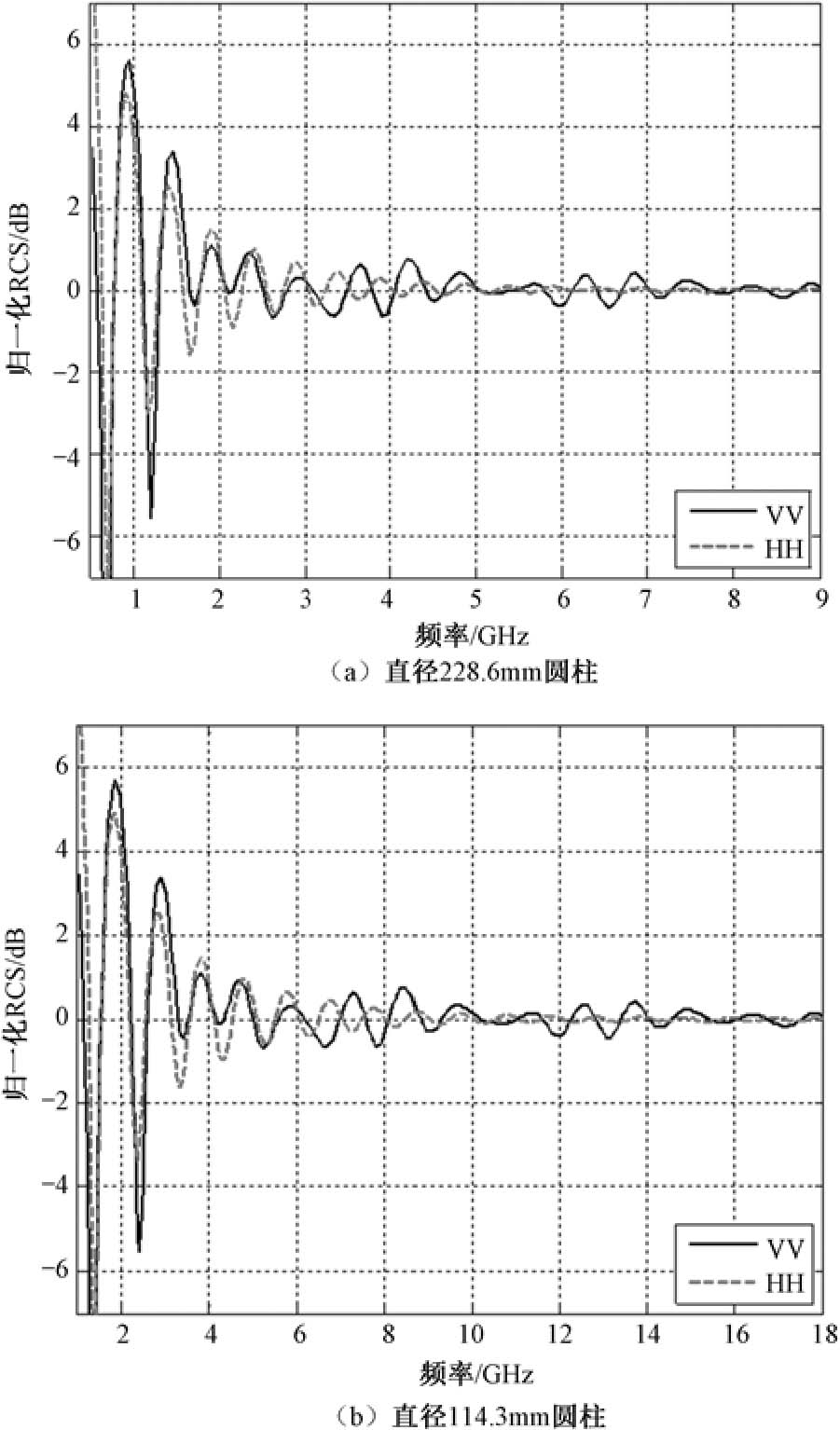
图2.46 不同尺寸圆柱定标体的归一化散射函数随频率的变化特性
从图2.45和图2.46还可看到,爬行波随频率升高而衰减的速度比行波分量要快得多。因为HH极化下,金属圆柱定标体的表面波散射分量仅由爬行波组成;而VV极化下,多种行波、爬行波散射分量并存,因此,VV极化下PO散射分量归一化后的散射函数,其振荡特性随频率衰减要比HH极化的慢得多。此外,电磁散射理论分析还表明,无论对于HH极化还是VV极化,金属圆柱定标体上被激发的各种表面波分量幅度均与镜面反射(也即PO散射分量)成正比,而相位则与传播路径长度成正比,后者取决于圆柱的直径和高度。
由此可见,只要给定高度和直径比,无论圆柱定标体尺寸如何改变,在给定极化下的归一化散射函数
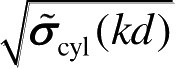 均是确定的函数,因此可以用同一个参数化模型来建模。为此,可通过MoM数值计算得到任何一个圆柱定标体的超宽带散射数据,然后采用复指数(CE)模型建立其参数化模型,根据缩比关系,该模型可推广用于任何其他具有相同高度和直径比的圆柱定标体的散射计算。上述原理构成了金属圆柱定标体RCS快速精确计算的核心基础。
均是确定的函数,因此可以用同一个参数化模型来建模。为此,可通过MoM数值计算得到任何一个圆柱定标体的超宽带散射数据,然后采用复指数(CE)模型建立其参数化模型,根据缩比关系,该模型可推广用于任何其他具有相同高度和直径比的圆柱定标体的散射计算。上述原理构成了金属圆柱定标体RCS快速精确计算的核心基础。
2. 圆柱定标体散射计算的CE 模型
CE模型 [104 -105] 可以用于建立目标散射快速精确计算的参数化模型,其基本思想是采用多个复正弦信号之和来表征复杂目标的散射函数,每个信号分量的幅度受到随雷达频率增长或衰减的色散因子的调制。
圆柱体的散射由镜面反射(PO散射分量)和表面波散射分量所构成,所有表面波分量均随频率升高而衰减。由此,经PO散射分量归一化后的圆柱体散射函数,随着频率升高其幅度终将等于1,故非常适合采用CE模型来建立其参数化模型。
金属圆柱定标体散射特性计算的CE模型可表示为
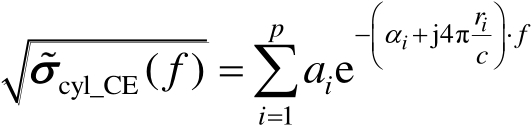
(2.124)
式(2.124)中, a i 、 α i 和 r i 分别表示复散射幅度、频率色散因子以及目标上第 i 个散射分量到目标参考中心的距离; c 为传播速度; p 为模型阶数,也即散射分量的个数(注意单个散射中心可能需要由多个分量来建模); f 为雷达频率。
给定一组经矩量法数值计算得到的圆柱定标体超宽带散射数据,CE模型的阶数可以通过文献[106-108]中的方法来确定,CE模型的参数可采用基于状态空间法(SSA)的算法 [106,108] 进行估计。关于模型阶数估计和参数估计的详细处理流程可参考文献[106],此处不再赘述。
3. 基于CE 模型的圆柱 定标 体 的 散射计算
根据式(2.122)~式(2.124),圆柱定标体的后向散射函数可由下式计算,即
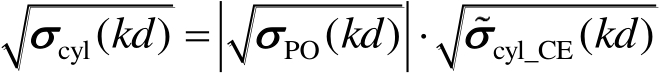
(2.125)
如前面所讨论的,对于给定的高度直径比,式(2.125)可用于任何尺寸的圆柱定标体的后向散射函数的精确计算,其RCS计算流程如图2.47所示。注意,无论采用多少个标准圆柱定标体,只需对其中一个给定尺寸的圆柱定标体的散射用矩量法数值计算,得到其精确超宽带散射数据,然后建立CE参数化模型,则该模型可以用于具有任何尺寸的同类圆柱定标体的散射计算。这样,最终有
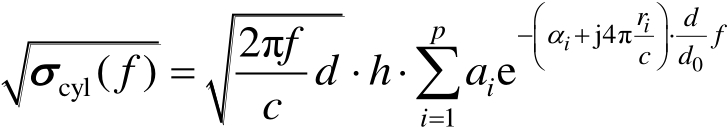
(2.126)
式(2.126)中, d 和 h 分别为圆柱定标体的直径和高度; d 0 为建立CE模型时所采用的矩量法计算数据所对应的圆柱的直径; a i 、 α i 和 r i ( i =1,2,⋯, p )为CE模型的参数,分别为复幅度、频率色散因子和到参考中心的距离; p 为模型阶数。
根据以上计算流程,对于给定高度和直径比(如7/15)的一组圆柱定标体,一旦建立了其参数化模型,则后续应用中只需利用该CE模型参数并根据缩比原理,完成任何同类圆柱定标体的散射计算,且可以保证计算的实时性。
同时,要注意HH和VV极化下,圆柱定标体的散射机理差异很大,因此,需要根据不同极化下的矩量法计算数据,建立不同的CE模型,分别用于HH和VV极化的散射计算。
必须指出,如果采用传统矩量法计算一个短粗圆柱定标体在0.5~40GHz频段内的精确RCS幅度和相位值,在常见的计算机服务器平台上可能至少耗费数周时间,而采用CE参数化模型,其计算时间仅在ms量级,且当 k d ≥5 时,计算不确定度在±0.03dB以内 [109] 。可见,这种参数化模型方法不但可以达到实时计算,而且计算结果的不确定度完全能够满足工程应用中对RCS测试标定的精度要求。
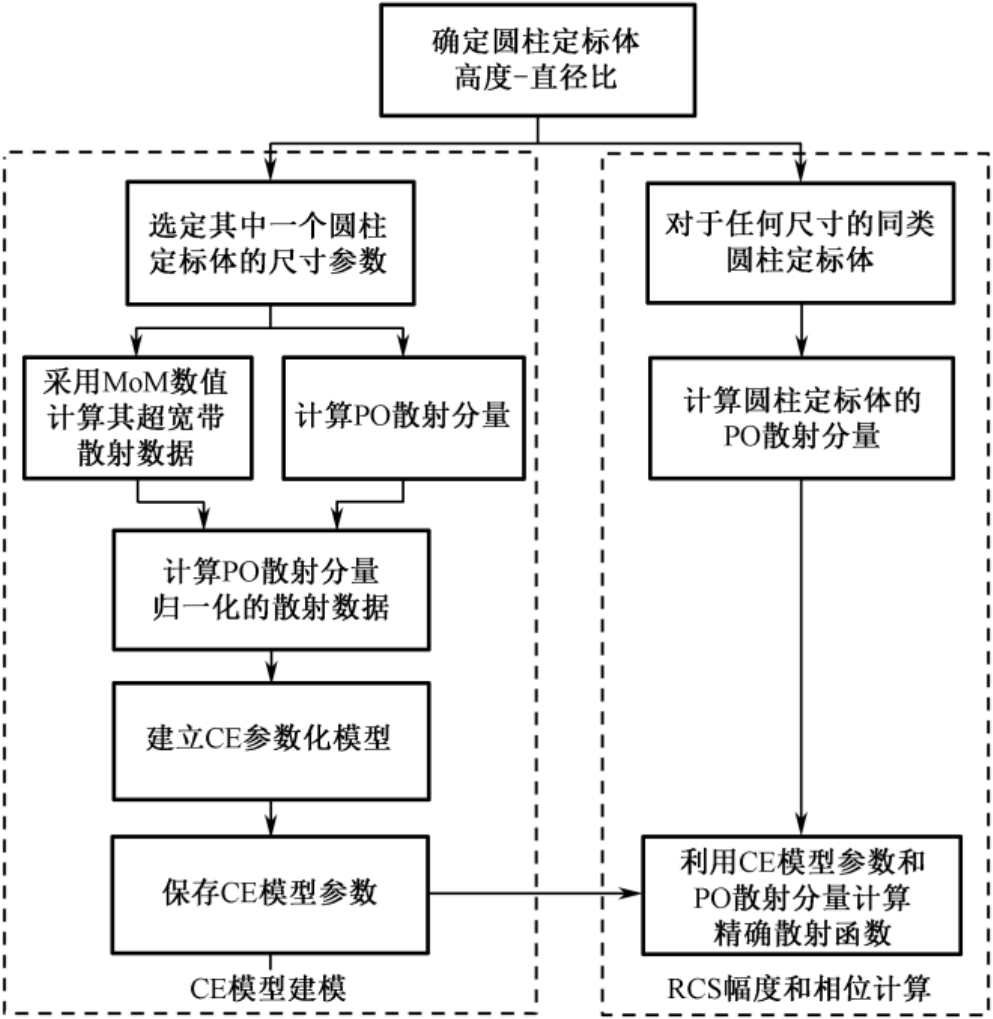
图2.47 圆柱定标体散射快速计算的CE模型建模和RCS计算流程
本书附录D中列出了对高度直径比为7/15的标准圆柱定标体散射计算的CE模型的MATLAB代码,尽管采用了参数化模型,但其计算精度足够高,且计算速度可达到准实时,完全可满足一般RCS测试工程的应用要求。