在雷达应用中,经常要计算多种目标的RCS,范围从简单目标(导体球、无限长圆柱等),到稍微复杂的目标(有限长圆柱、有限弯板等),再到复杂目标(飞机、舰船等)。构成目标的材料可能是金属,也可能是介质或磁性材料,或是全部或部分这样的材料涂覆层。尽管这样的外形和材料的组合为目标RCS的控制提供了更多的自由度,但是也增加了解析和数值计算的复杂性。
已经提出了多种解析方法用于确定外形、尺寸和材料变化很宽的目标的RCS。这些方法大致可以分为两大类:精确方法和近似方法。精确方法用公式描述边值问题,并利用满足合适的精确边界条件的波动方程的精确解来获得问题的答案。由于精确方法在权威的文献 [17-18] 中已做详尽的讨论,因此这里将不再赘述。然而,即便是精确方法,最后的数值结果也要通过做某些形式的近似(如无限级数的截断)而得到。在这种意义上,所谓精确方法其实也是近似的,尽管对特定的问题它们可以给出足够准确的结果。
可是,在电磁学中,实际感兴趣的问题很少能用精确方法求解,这是因为精确方法仅适用于具有符合坐标系使得波动方程可以分离的一类几何结构的散射问题。于是,在过去的几十年间,人们提出了大量近似而准确的方法进行求解。这些方法一般建立在麦克斯韦方程 [19] 的一些渐近解或者与边界条件有关的一些简化假定的基础之上。近似方法虽被用于求解绝大多数实际感兴趣的问题,但是其中一些方法具有严重的局限性,必须进行修正以适应特殊问题的需要,如考虑结构的有限性和相关的边缘影响或表面行波(或爬行波)和多次绕射效应。
尽管有多种近似方法可供使用,然而,没有哪种单一的方法对所有的问题都是够用的,因此人们提出了组合两种或更多方法优点的混合方法 [20-21] 。许多实际感兴趣的复杂目标的散射一般并不适合于用近似解析方法求解,为此又常采用数值法,通过数值求解包含在积分方程中的未知感应电磁流来获得问题的解。
一些已出版的书籍 [17-19,22-27] 很好地讨论了目标RCS的预估方法(包括解析的和数值的),1965年和1989年出版的两本RCS专辑 [28-29] ,为了解RCS的预估方法提供了极好的信息来源,本节的部分内容参考或引用了这些内容。本节的目的不是发展各种近似的解析和数值方法,而是将它们进行简要归纳,并比较它们的优缺点,以方便阅读者能够对于具体的目标决定采用哪一种方法进行计算更能获得满足要求的结果。
几何光学(Geometrical Optics,GO)法是一种高频(或零波长)近似,它用经典的射线管来说明散射机理和能量传播,因此,又被称为射线光学法。可将与横向电磁(TEM)波相关的复电场或磁场写成
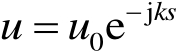
(2.48)
式(2.48)中, u 0 是复幅度; k =2π/ λ ( λ 为波长)是自由空间波数; s 是沿着射线测量的观察面和参考面之间的距离。
当目标被窄波束雷达发射的电磁波照射时,如果目标的尺寸与雷达波长相比足够大,那么雷达回波似乎来自目标上的一些特殊点。这些点(有时称为反射点)是波经历镜面反射(即入射角等于反射角)的点,可以看成散射中心。在这种近似下,可以不必考虑整个目标的贡献,只需对这些散射中心进行适当组合就足以描述在给定方向上的散射。如果给定了目标、入射面和观察面以及双站角,则可以用点
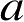 和
b
之间的最短路径的费马原理确定散射中心,即
和
b
之间的最短路径的费马原理确定散射中心,即
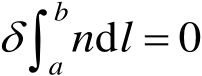
(2.49)
式(2.49)中,
δ
表示变分;
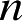 为介质的折射率。
为介质的折射率。
在射线管起始端和结束端的场之间的关系可通过能量守恒定律得到。如图2.7所示,在观察端的电场强度 E ( s )可用参考端( s =0)的电场强度 E (0)表示为
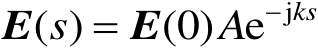
(2.50)
式(2.50)中,扩散因子为
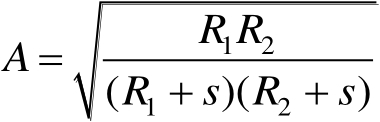
(2.51)
式(2.51)中,
R
1
和
R
2
为射线管结束端波形的主曲率半径。不难看出,满足
R
1
+
s
或
R
2
+
s
等于零的点或线段构成了所谓的“焦散”。在焦散处,式(2.50)表示的场是无效的。对平面波,
R
1
=
R
2
=
∞
,由式(2.51),
A
=1;类似地,对球面波,
R
1
=
R
2
=
R
,且
A
=
R
/(
R
+
s
);对柱面波,
R
1
=
∞
,
R
2
=
ρ
,故
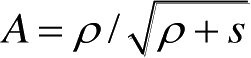 。这里,
ρ
是柱面波前的曲率半径。扩散因子考虑了波传播过程中能量的扩散和场强的衰减,而这些在反射和传输系数中通常不予考虑。
。这里,
ρ
是柱面波前的曲率半径。扩散因子考虑了波传播过程中能量的扩散和场强的衰减,而这些在反射和传输系数中通常不予考虑。
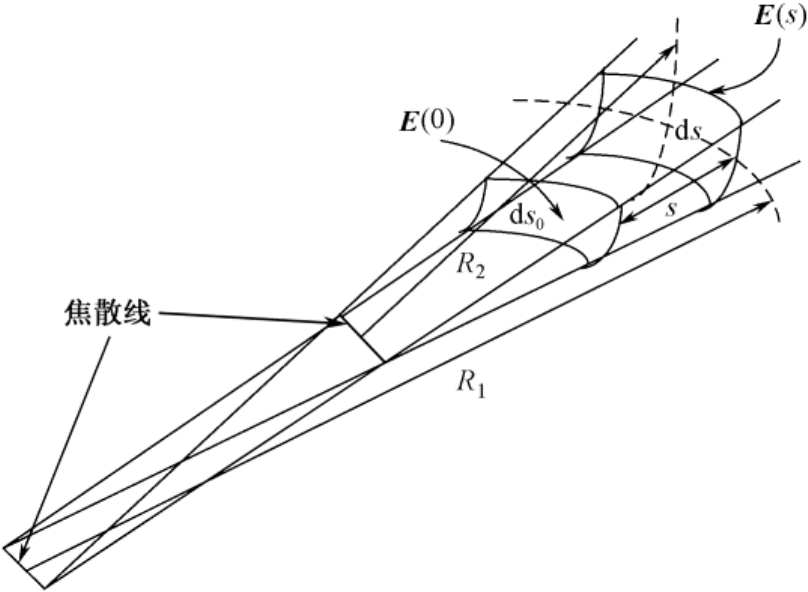
图2.7 主曲率半径为 R 1 和 R 2 的波前
Luneberg-Kline [19] 将场表示成 ω 的负幂级数展开式,即
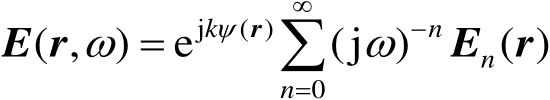
(2.52)
式(2.52)中, ψ ( r )是相位因子。很显然,几何光学场就是Luneberg-Kline级数的首项( n =0)。在几何光学近似中,将空间区域划分成照明区和阴影区,因此该方法不能考虑任何绕射效应。
在所有的散射表述中,一个基本问题是确定目标上的感应电磁流,只要求得感应电磁流,散射场和其他的量就可以用标准的方法进行计算。物理光学(Physical Optics,PO)法是一种高频方法,它用充当散射场激励源的感应表面电磁流来代替目标。为获得表面电磁流,将做下列基本假定:①表面的曲率半径与波长相比足够大;②表面电磁流仅存在于被入射波直接照明的区域,且照明表面上的电磁流和入射点处与目标表面相切的无限大平面上的电磁流有相同的特性。
对理想导体目标,目标照明面的物理光学电流为
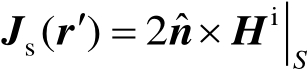
(2.53)
对于一般的目标,所要求的电磁流可以根据上面给出的两个基本物理假定用Schelkunoff等效原理 [17] 获得。
基于目标表面电磁流分布的选择以及其他的特性,文献[30]讨论了物理光学法的12种形式。目标表面电磁流的三种可能选择是
E - H -公式:
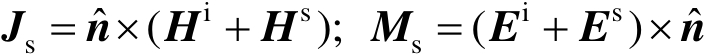
(2.54)
H -公式:
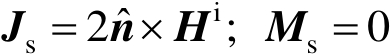
(2.55)
E -公式:
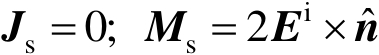
(2.56)
式中, E i , H i 和 E s , H s 分别是目标表面上的入射场和散射场,通过适当的边界条件相联系。
一般来说,物理光学流是作为未知量出现在积分方程(见2.2.7节)中的,积分方程的解提供了场计算所需要的电磁流。根据这一观点,忽略沿观察方向的任何表面流的影响,由Stratton-Chu方程(见2.2.7节)可得远区( r → ∞ )散射场 [25] 为
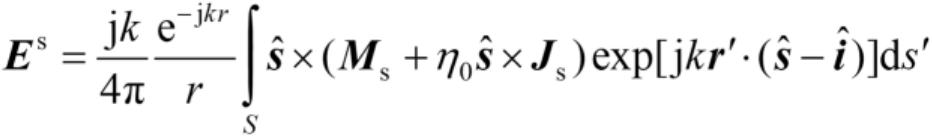
(2.57)
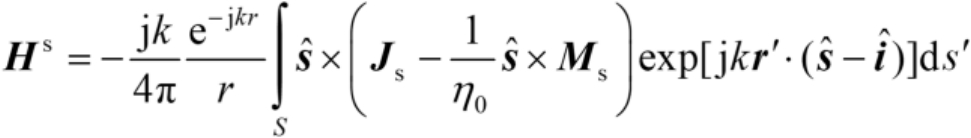
(2.58)
式中,
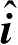 和
和
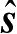 是入射方向和观察方向的单位矢量;
S
表示目标表面的照明部分,其他参数如图2.8所示。注意,在式(2.57)和式(2.58)中,
J
s
,
M
s
表示由式(2.54)给定的面
S
上电磁流的矢量幅度,其中的相位因子已经被分离出来,并包含在指数项中。可以将式(2.57)和式(2.58)认为是广义的物理光学公式,用于已知电磁流
J
s
和
M
s
求散射场。但对导体目标,普遍选用式(2.55)。
是入射方向和观察方向的单位矢量;
S
表示目标表面的照明部分,其他参数如图2.8所示。注意,在式(2.57)和式(2.58)中,
J
s
,
M
s
表示由式(2.54)给定的面
S
上电磁流的矢量幅度,其中的相位因子已经被分离出来,并包含在指数项中。可以将式(2.57)和式(2.58)认为是广义的物理光学公式,用于已知电磁流
J
s
和
M
s
求散射场。但对导体目标,普遍选用式(2.55)。
物理光学法是求解高频RCS问题的常用方法,因为它不要求对焦散和阴影边界做特殊处理。物理光学解中所包含的表面积分可以通过将表面离散为一定数量的多边形面元,再利用Gardon [31] 的处理办法就很容易解决。文献[32]给出了经过这种处理的任意各向异性材料涂覆导体目标散射的物理光学解析表达式。通过改进假定的电流分布能够改善物理光学法的准确性。物理光学法不能考虑目标上存在的不连续性,不能预估简单散射体的单站散射退极化效应。但是,对单站多次散射,它是能预估退极化效应的。一般来说,用物理光学法获得的场是不满足互易性的。可是,两种解(一种是对给定发射机和接收机位置的解,另一种是对它们的位置互换后的解)的平均,还是满足互易性的。因此,单站或后向散射解自动满足互易性。文献[33]对与复杂目标后向散射有关的一些参量的不同的和特殊的计算进行了讨论。
图2.8 目标表面的电磁散射
克服几何光学近似存在的缺陷的第一个主要贡献是由J. B. Keller提供的,他从考虑直劈对电磁波的散射出发,推导了几何绕射理论(Geometrical Theory of Diffraction,GTD)的公式,并用于计算绕射和极化效应 [34] 。按照反射和传输类推的方式,Keller引入了绕射系数和绕射线,通过将近似场与在对无限长直劈的精确Sommerfeld解中的绕射积分进行渐近计算之后获得的场相比较,获得了绕射系数的直观表达式。
Keller给出的无限长直劈(见图2.9)绕射系数 [34] 为
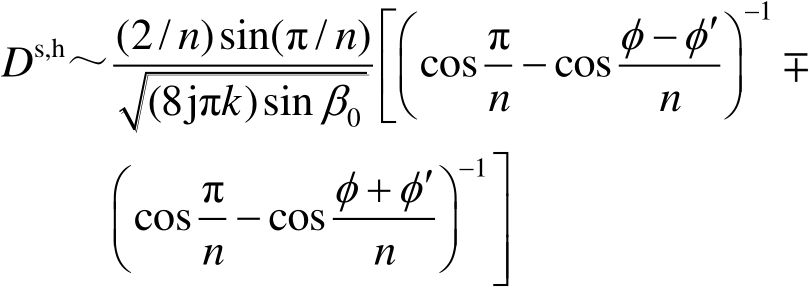
(2.59)
式(2.59)中,
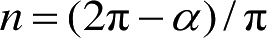 ,
α
是内劈角(见图2.9);
β
0
是在绕射点
Q
E
处入射线与直线边缘之间的夹角中较小的一个;
ρ
′,
ρ
(见图2.9)分别是入射线和绕射线在垂直于边缘的平面上的投影;
ϕ
′,
ϕ
分别是入射角和散射角;上标“s”和“h”分别代表软(
E
z
=0)劈和硬(∂
H
z
/∂
n
=0)劈,且分别对应式(2.59)“∓”中的“–”和“+”。
,
α
是内劈角(见图2.9);
β
0
是在绕射点
Q
E
处入射线与直线边缘之间的夹角中较小的一个;
ρ
′,
ρ
(见图2.9)分别是入射线和绕射线在垂直于边缘的平面上的投影;
ϕ
′,
ϕ
分别是入射角和散射角;上标“s”和“h”分别代表软(
E
z
=0)劈和硬(∂
H
z
/∂
n
=0)劈,且分别对应式(2.59)“∓”中的“–”和“+”。
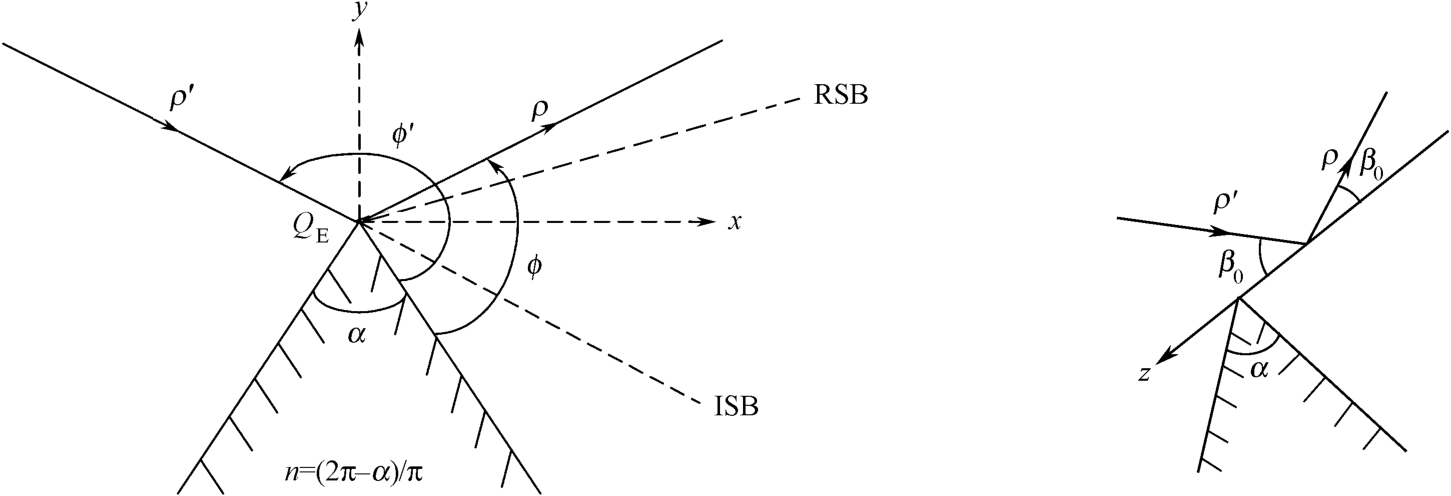
图2.9 无限长直劈对平面波的绕射
对一般的入射波,绕射场与入射场的关系可以表示为
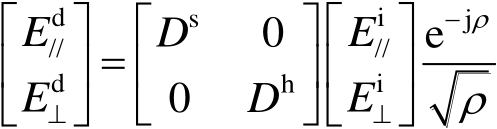
(2.60)
式(2.60)中, ρ 是边缘与观察者之间的距离;下角标// 和⊥ 分别表示电场平行和垂直于入射面(入射线与边缘构成的平面)。
Keller的理论对直角圆锥和圆柱的后向散射 [35-36] 给出了很好的结果,GTD的结果比物理光学的结果与实验吻合得更好。尽管GTD已成功地用于许多实际感兴趣的问题,但它还是有一些局限性:
(1)当绕射场在入射和反射阴影边界(ISB和RSB)时为无穷大;
(2)绕射系数在边缘上为无穷大,因此违反了边缘条件;
(3)仅通过与已有的典型问题的精确解相比较获得绕射系数的表达式,因此不能构成完整的理论体系;
(4)不能确定绕射波表达式的高阶项;
(5)在焦散处的解是奇异的。
尽管如此,Keller的GTD对随后的电磁学中多种渐近绕射理论的发展还是产生了深远的影响。
许多研究着重于改进2.2.3节描述的GTD的局限性,目的是在阴影边界或接近阴影边界处获得绕射的一致性解,这主要有两种成功的方法。
第一种方法基于边缘绕射问题中场的解,可以用与菲涅耳积分有关的特殊渐近级数展开的假定,由Ahluwalia, Lewis和Boersma [37] 三人提出,称为绕射的一致性渐近理论(Uniform Asymptotic Theory,UAT)。文献[37]描述了确定渐近级数中对应波数 k 所有阶次的系数的一种系统化的程序。UAT的解在接近和远离阴影边界时都是有效的,也已用于曲劈的绕射 [38-39] 以及三维半平面的绕射 [40] 。
第二种称为一致性绕射理论(Uniform Theory of Diffraction,UTD)的流行方法是由Kouyoumjian和Pathak [41] 提出的。在UTD中,Keller的绕射系数被一个与菲涅耳积分有关的乘法因子所修正,结果被推广到至少有一面是曲面的一般曲劈的情况。当场点趋于阴影边界时,乘法因子趋于零,因此补偿了Keller的绕射系数的奇异性,使得场在阴影边界是有限的。
虽然很多文献对UAT和UTD及其应用都做了很好的阐述,但是相比之下,还是UTD应用得更为广泛。因此,这里只简单概述Kouyoumjian和Pathak的关于UTD的基本要点。
图2.10所示为曲劈对电磁波的绕射。在阴影边界附近具有一致性的绕射系数 [41] 为
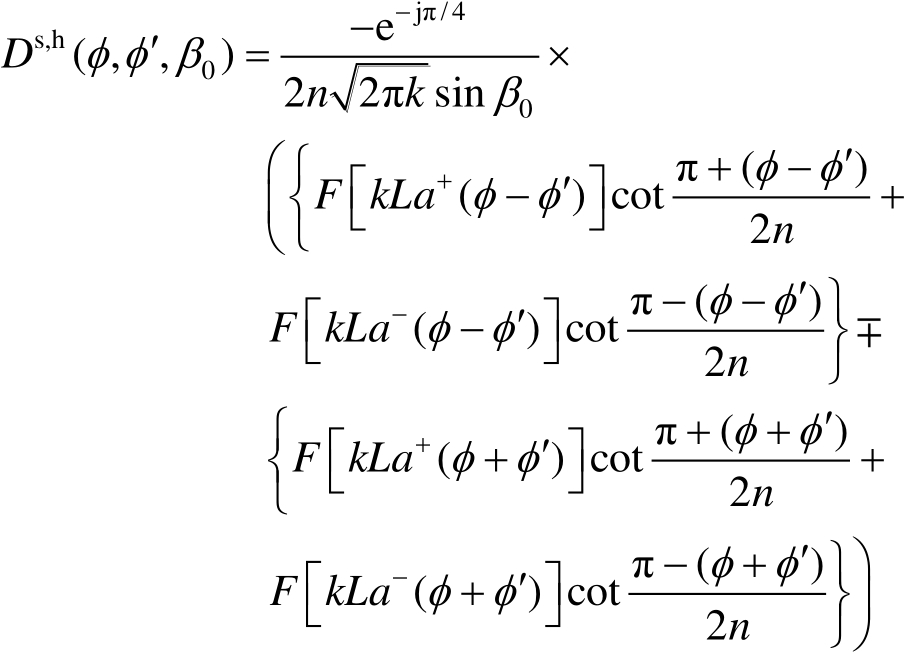
(2.61)
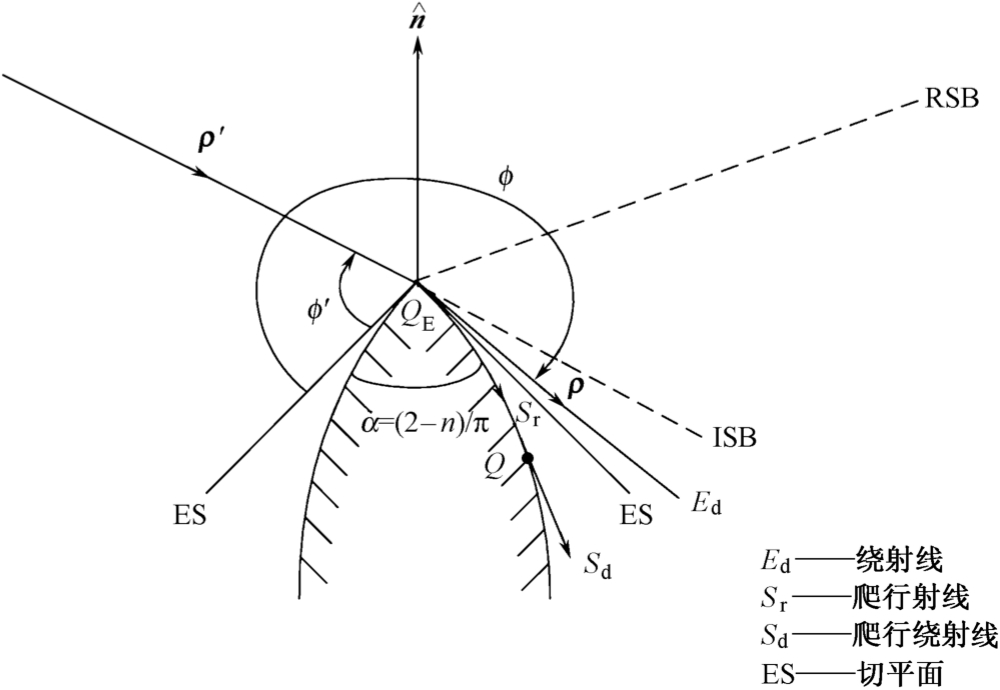
图2.10 曲劈对电磁波的绕射
式(2.61)中
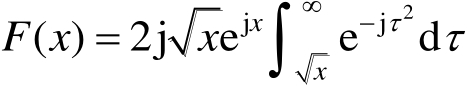
(2.62)
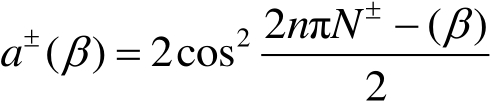
(2.63)
这里, N ± 是最接近满足下列方程的整数,即
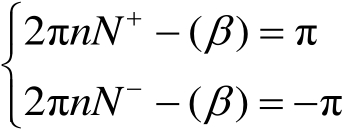
(2.64)
L 是距离参数,定义为:
对平面波入射,
L
=
s
sin
2
β
0
;对柱面波入射,
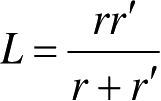 ;对锥面波和球面波入射,
;对锥面波和球面波入射,
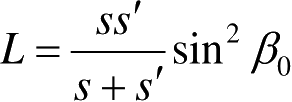 。其中,
r
′为垂直入射到边缘上柱面波的曲率半径;
r
是场点到边缘的垂直距离;
s
′和
s
分别是沿射线从边缘到源点和场点的距离;
β
0
是入射线与绕射点
Q
E
处边缘切线之间的夹角中较小的一个。
。其中,
r
′为垂直入射到边缘上柱面波的曲率半径;
r
是场点到边缘的垂直距离;
s
′和
s
分别是沿射线从边缘到源点和场点的距离;
β
0
是入射线与绕射点
Q
E
处边缘切线之间的夹角中较小的一个。
由式(2.62)给出的是修正的菲涅耳积分,可近似为
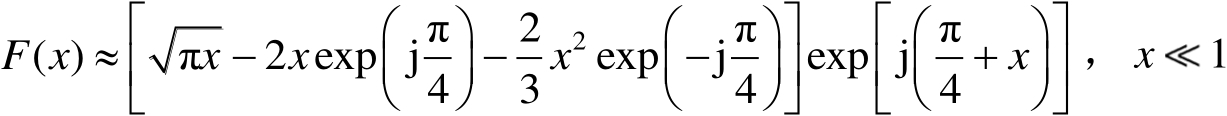
(2.65)
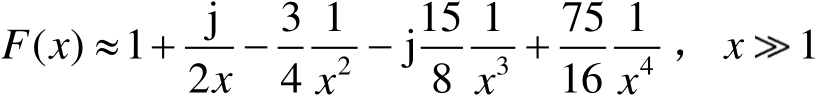
(2.66)
当 x > 10 时, F ( x )→1。
半平面( n =2)绕射是一种特殊的情况,相应的绕射系数很容易通过式(2.61)得到,可参见文献[41-42]。
当源很接近边缘时,绕射系数式(2.61)需要做与入射场强沿劈边缘变化有关的修正,这就是一致性斜率绕射修正 [43] 。一致性斜率绕射系数 [43] 为
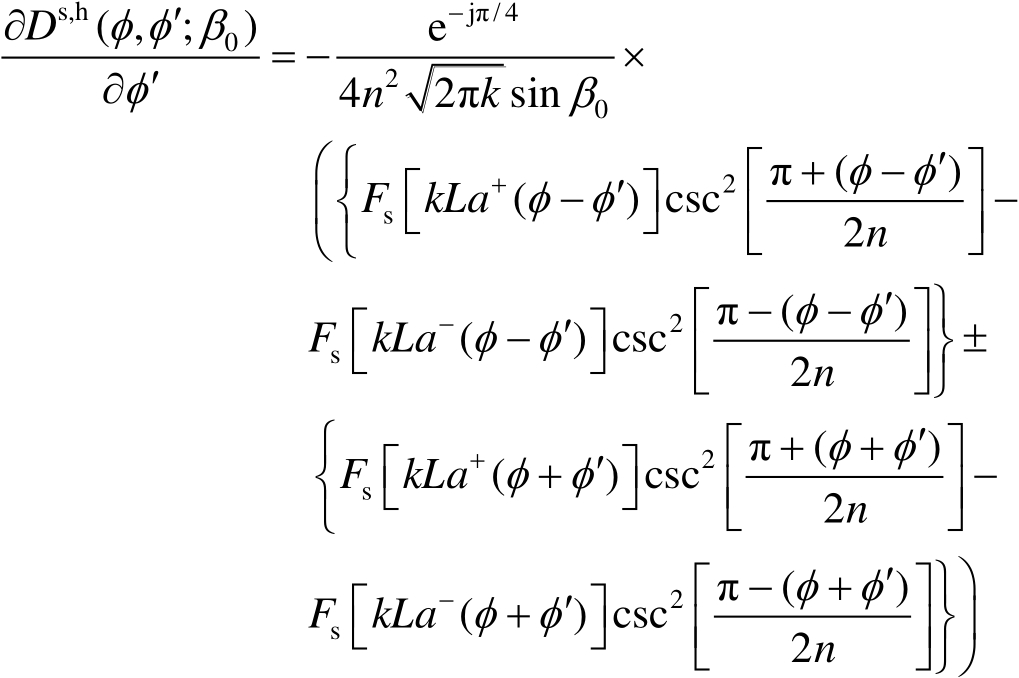
(2.67)
式(2.67)中
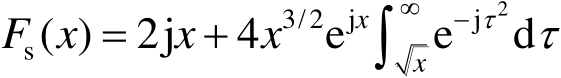
或
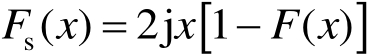
在阴影边界,利用下面的限制有
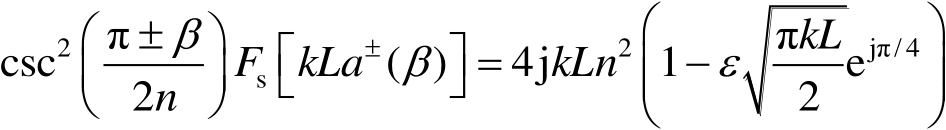
式中,
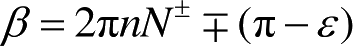 ,
ε
是一个很小的数。
,
ε
是一个很小的数。
UTD已被成功地应用于许多散射和天线问题。事实上,它是在解决实际问题中最流行的高频渐近方法之一。考虑到一致性绕射系数式(2.61)在工程中很常用,附录A给出了它的FORTRAN计算程序 [44] ,其中子程序中的输入和输出变量对应如下(其中等式左边表示子程序中的变量,等式右边表示式(2.67)中的变量):(DS, DH)= D s,h ,R= L (以波长为单位),(PH, PHP)=( ϕ , ϕ ′),BO= β 0 ,FN= n 。例如,若R=3 λ ,PH=250°,PHP=75°,BO=90°,FN=2,则DS= -0.748-j0.19,DH= -0.628+j0.0735。
由于射线方法(GTD、UAT和UTD)的基本性质,它们在结构的焦平面上要遇到奇异性,因此不能在焦散处提供正确和有限的场。圆口径和圆盘或旋转体上的环形斜率不连续处的轴线方向都是焦散的例子。焦散处的场必须单独计算,有几种不同的方法可以完成这种计算。
首先,通过将标量波动方程的渐近展开式与用绕射系数和射线光学得到的发散结果进行比较,Keller [45] 提出了一个修正因子,用GTD的解乘以这个修正因子之后可以得到焦散处场的合理估计。
第二种方法用2.2.2节描述的物理光学法。
第三种方法用边缘等效电磁流法 [46] ,这也是应用很广泛的方法。这种方法直接组合等效电磁流来移去GTD解的奇异性。如图2.11所示,考虑平面波从 x z 面入射到位于 x y 面上的金属圆盘的情况,等效边缘电磁流 I e 和 I m 分别为 [46]
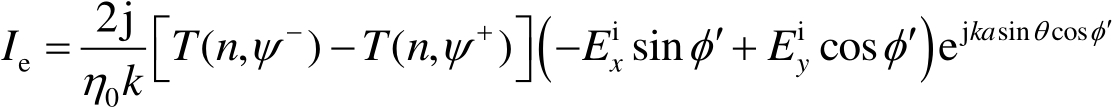
(2.68)
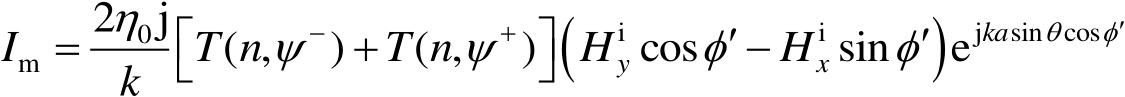
(2.69)
式中
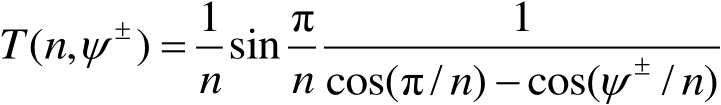
(2.70)
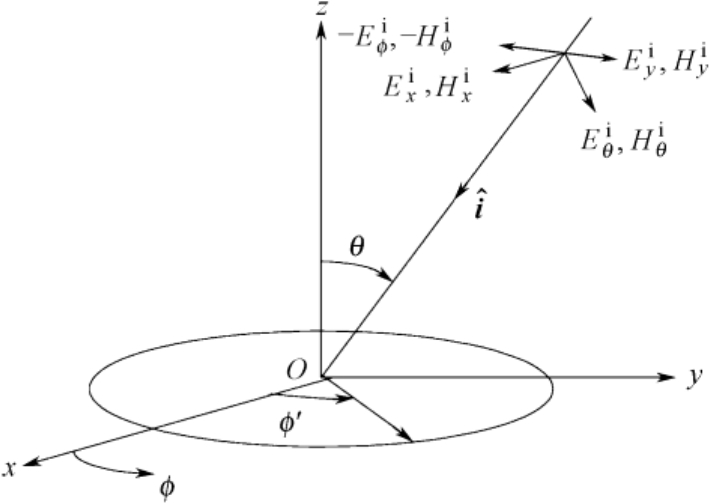
图2.11 载有等效边缘电磁流的导线环
式中,
n
是前面定义的劈角;
η
0
=377Ω;
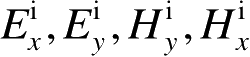 是在边缘上入射点处的入射场的直角坐标分量。这些电流不包括几何光学项。对实际情况,沿着口径或圆盘的边缘利用这些电磁流可以确定所希望的焦散场。例如,如图2.11所示,通过利用环上的电流
I
e
,可以得到平面波照射的圆环的后向散射场为
是在边缘上入射点处的入射场的直角坐标分量。这些电流不包括几何光学项。对实际情况,沿着口径或圆盘的边缘利用这些电磁流可以确定所希望的焦散场。例如,如图2.11所示,通过利用环上的电流
I
e
,可以得到平面波照射的圆环的后向散射场为
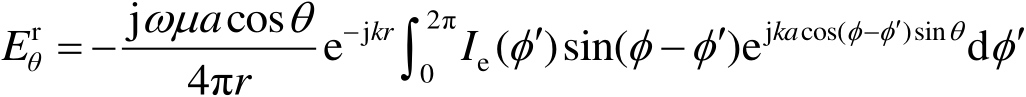
(2.71)
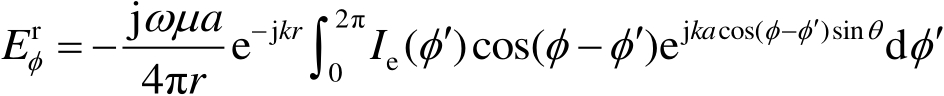
(2.72)
载有磁流的环的场可以通过二重性原理 [18] 而获得。
虽然边缘等效电磁流法的提出最初是为了计算焦散处的边缘绕射场,但是它也可以用来计算任意边缘的绕射场。等效边缘电磁流有多种形式,其中以Mitzner
[47]
的增量长度绕射系数和Michaeli
[48]
给出的等效电磁流较为常用,这里考虑Michaeli的表达。对边缘为
 的任意劈,它的远区边缘绕射场可表示为
的任意劈,它的远区边缘绕射场可表示为
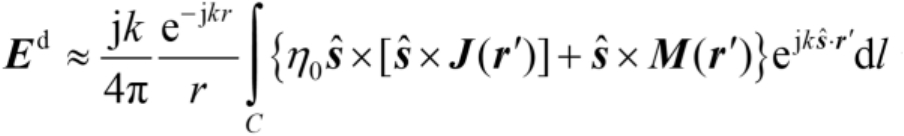
(2.73)
式(2.73)中,
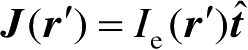 和
和
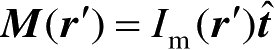 分别是等效边缘电磁流;
分别是等效边缘电磁流;
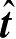 是
C
的切向单位矢量;
是
C
的切向单位矢量;
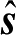 是观察方向的单位矢量;
r
′是从原点到边缘上某点的径向矢量;d
l
是沿
C
的弧长增量。参考图2.12中有关定义,文献[48]给出的
I
e
(
r
′)和
I
m
(
r
′)的表达式为
是观察方向的单位矢量;
r
′是从原点到边缘上某点的径向矢量;d
l
是沿
C
的弧长增量。参考图2.12中有关定义,文献[48]给出的
I
e
(
r
′)和
I
m
(
r
′)的表达式为
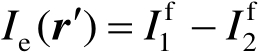
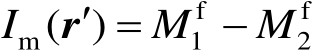
式中,
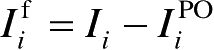 ,
,
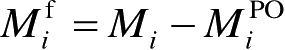 ,
i
=1,2,且
,
i
=1,2,且
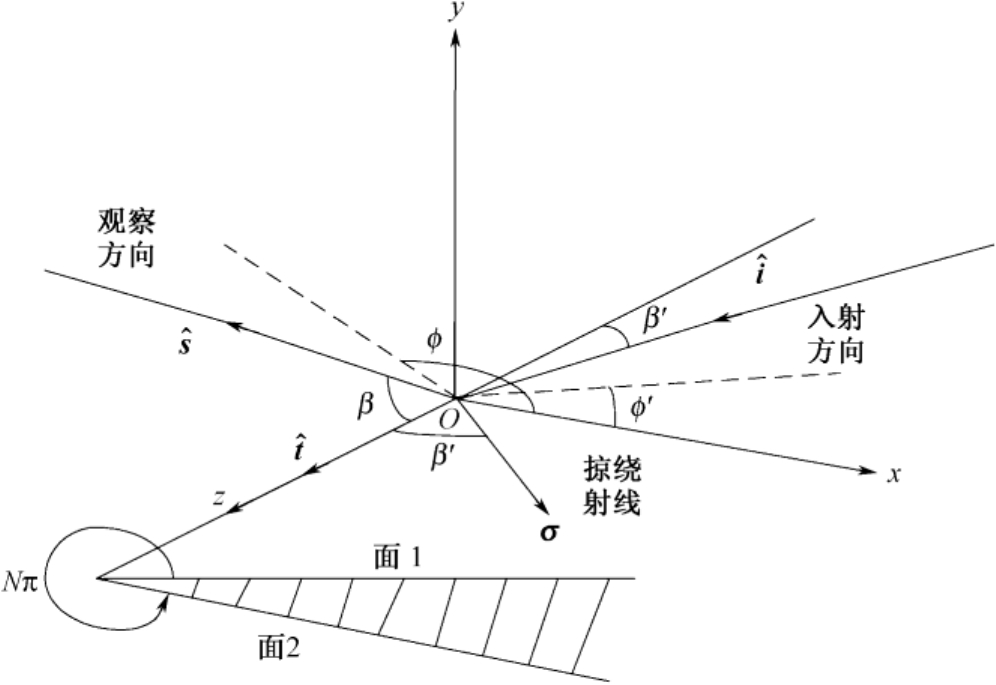
图2.12 劈散射的几何结构(虚线表示入射和观察方向在 x y 平面的投影)
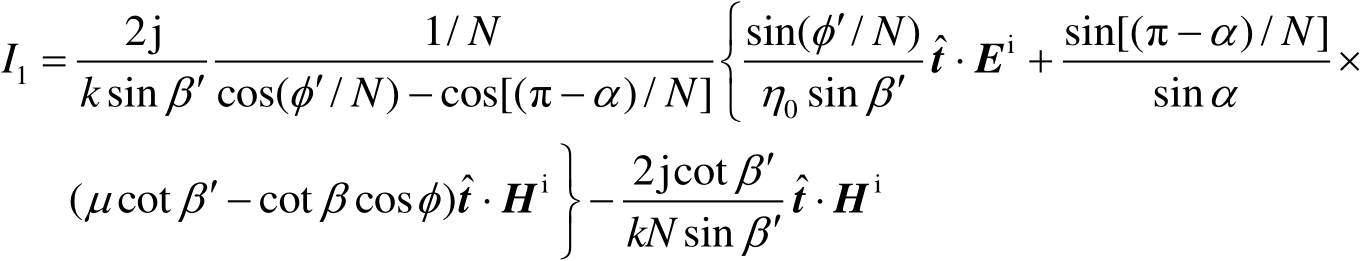
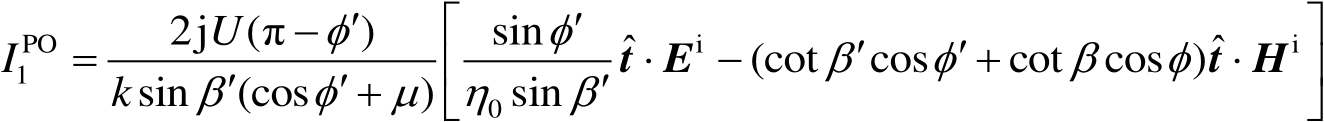
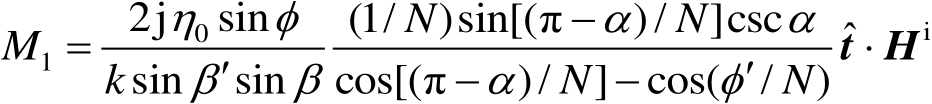
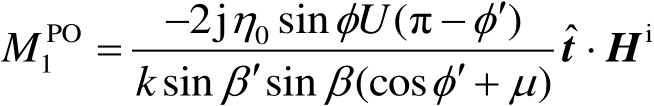
式中,
N
π 为外劈角(
N
>
1);
E
i
和
H
i
是
O
点处的入射电磁场;
U
(π−
ϕ
′)是单位阶跃函数(当π−
ϕ
′
>
0 时为1,当π−
ϕ
′
<
0 时为0);
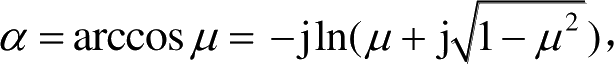 μ
=(cos
γ
−cos
2
β
′)/sin
2
β
′,
μ
=(cos
γ
−cos
2
β
′)/sin
2
β
′,
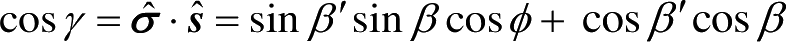 。在以上各式中,只要应用下列代换
。在以上各式中,只要应用下列代换
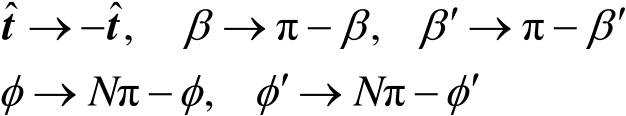
就可得到下标为“2”的量,即
 和
和
 。
。
式(2.73)中的线积分一般要用数值方法求解。可是,如果将边缘 C 用若干根直线段来逼近,则对每段直线边缘,该积分是解析可积的。通过叠加所有被照明直线边缘的绕射场就可以得到劈边缘的绕射场。上述表达式具有通用性,因此对每一种形状无须重新处理。
以图2.13所示的金属平板作为式(2.57)和式(2.73)的应用计算举例,图2.14给出了 ϕ i =30° 时该金属平板后向RCS随 θ i 的变化曲线。
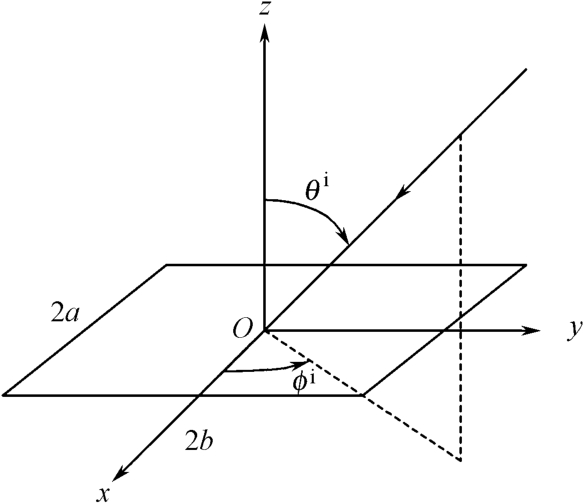
图2.13 金属平板
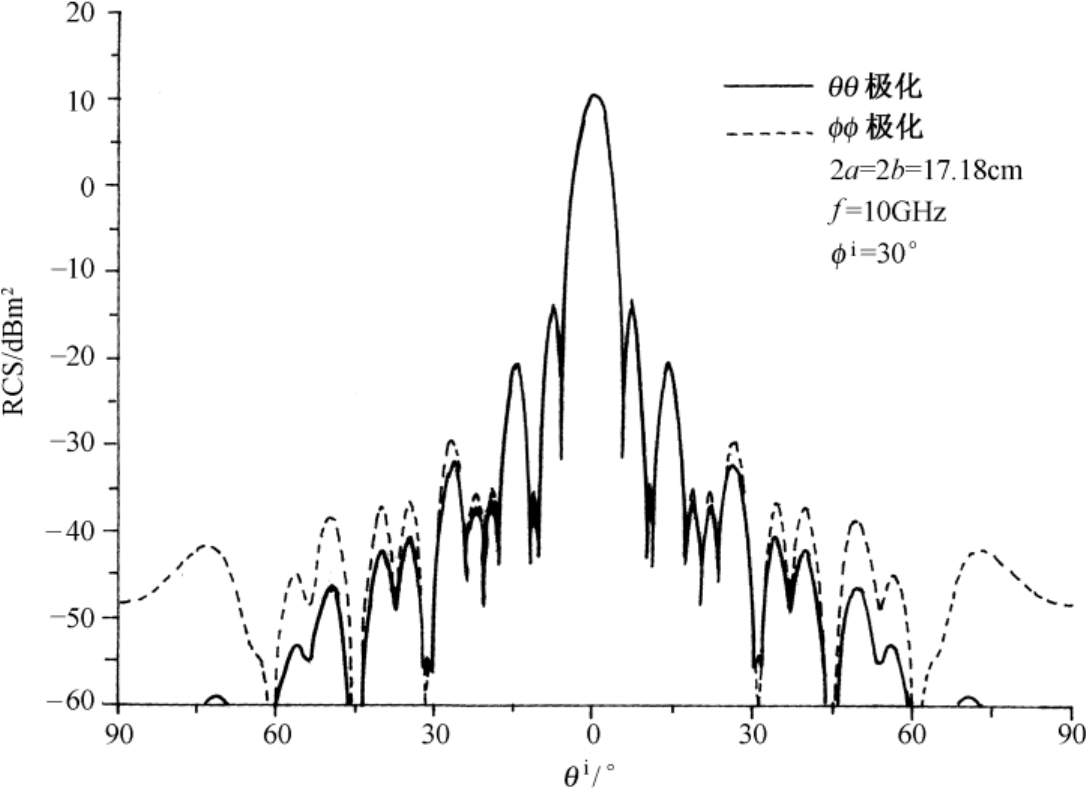
图2.14 ϕ i =30° 时金属平板后向RCS随 θ i 的变化曲线
弹跳射线(Shooting and Bouncing Ray,SBR)法最初是由S. W. Lee等人 [49 -50] 提出用于计算腔体目标RCS的一种高频方法,后来被推广到包括复杂目标(含材料)在内的一般性目标的多次反射计算 [51-53] 中。为了计算多次反射效应,Lee的方法 [50] 将电磁波等效成图2.15所示的一条条射线管,按几何光学原理分别追踪每条入射到口径面(口面)∑ A 上的射线管,直到这条射线管在腔体内经过多次反射后再次投射到口径面,即射线管离开散射体为止。在追踪射线过程中,由于极化、腔壁损耗、扩散因子、相位滞后等因素的影响,需要对每根射线进行场强追踪,最后在返回口面的射线管上进行口面积分 [49] ,求出它的远区散射场。对每条射线管做积分计算得到它的远区散射场,再对所有射线管的远区散射场求和,即为总的远区散射场。具体计算过程主要分为三步:一是给定腔体的几何结构和入射场,通过射线追踪寻找射线路径,这部分问题仅与目标的几何结构有关;二是根据几何光学定理确定口面上出射射线场的幅度,这部分问题涉及计算射线管的扩散因子和反射系数;三是用Kirchhoff近似(物理光学近似)确定后向散射场和RCS。
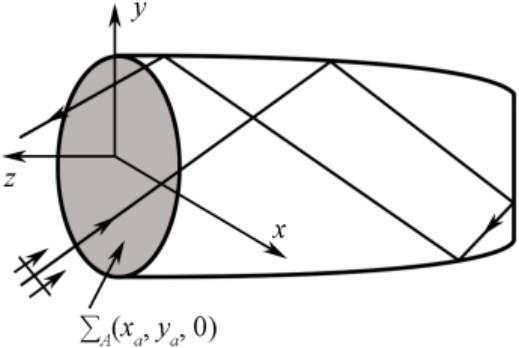
图2.15 弹跳射线法示意图
对于复杂目标而言,上述SBR方法在实际使用中存在以下难点:
(1)复杂目标的外形一般无法用解析式表达,这给传统意义上的射线与目标表面的求交运算,以及扩散系数的准确求解等运算带来很大困难。
(2)为了保证计算精度,射线管的面积必须足够小,射线管的边长一般取为入射波长的1/10左右。因此,电大尺寸复杂目标的射线追踪计算量将非常巨大,常规通过数值解法求交的运算效率很低,基本不能胜任。
(3)复杂目标一般并不存在明确的口面∑ A ,因此选择在目标口面上划分射线管并进行射线追踪,再利用口面积分计算射线管散射贡献的方法实现起来并不容易。
随着有限元技术的快速发展,采用三角/四边形小平面元网格来分片拟合复杂曲面,可以实现对任意形状复杂目标的精确描述,再利用针对面元模型的曲率重构方法 [54] ,则能有效解决具有复杂曲面结构的目标扩散系数计算时,准确获取所需曲率信息的难题。因此,基于平面元模型的SBR方法是目前被广泛采用的一种计算多次反射的有效方法,解除了Lee的方法中模型需要解析表达的限制,大大拓展了能够求解复杂目标的范围 [55-57] 。该方法首先将入射平面电磁波离散为若干密集的射线管,然后通过射线追踪确定各弹跳射线的路径,再利用几何光学法计算各个射线管的场,最后选择射线管在目标表面投射区域上进行物理光学积分求出射线管的散射场。下面就这种方法涉及的四个关键问题加以详细讨论。
(1) 射线管的自动划分 。 考虑到复杂目标一般没有明确的口面,为确定射线发射的源点需要确定一个“等效的发射面”,再在该发射面上进行射线管划分,进而完成射线追踪过程。
这里选择一种较为简便的方法自动划分射线管。如图2.16所示,将平面元模型的包围盒沿入射方向
 的反方向投影到目标体外的一个垂直于
的反方向投影到目标体外的一个垂直于
 的平面上,投影区域通常为一凸多边形(例如,图2.16中的五边形
P
1
P
2
P
3
P
4
P
5
),将该多边形用一个最小的长方形包围,以确定“等效发射面”的范围,同时建立相应的局部坐标系
x
c
y
c
z
c
,选择长方形的一个角点作为坐标原点
O
c
,最后根据多次反射计算精度的要求,一般按
l
p
=
λ
/10 的间隔(也可根据目标的复杂程度进行调整)在发射面上划分出射线管。由于“等效发射面”垂直于入射方向,这与入射平面波的假定一致,因此有利于多次反射中相位延迟的处理。
的平面上,投影区域通常为一凸多边形(例如,图2.16中的五边形
P
1
P
2
P
3
P
4
P
5
),将该多边形用一个最小的长方形包围,以确定“等效发射面”的范围,同时建立相应的局部坐标系
x
c
y
c
z
c
,选择长方形的一个角点作为坐标原点
O
c
,最后根据多次反射计算精度的要求,一般按
l
p
=
λ
/10 的间隔(也可根据目标的复杂程度进行调整)在发射面上划分出射线管。由于“等效发射面”垂直于入射方向,这与入射平面波的假定一致,因此有利于多次反射中相位延迟的处理。
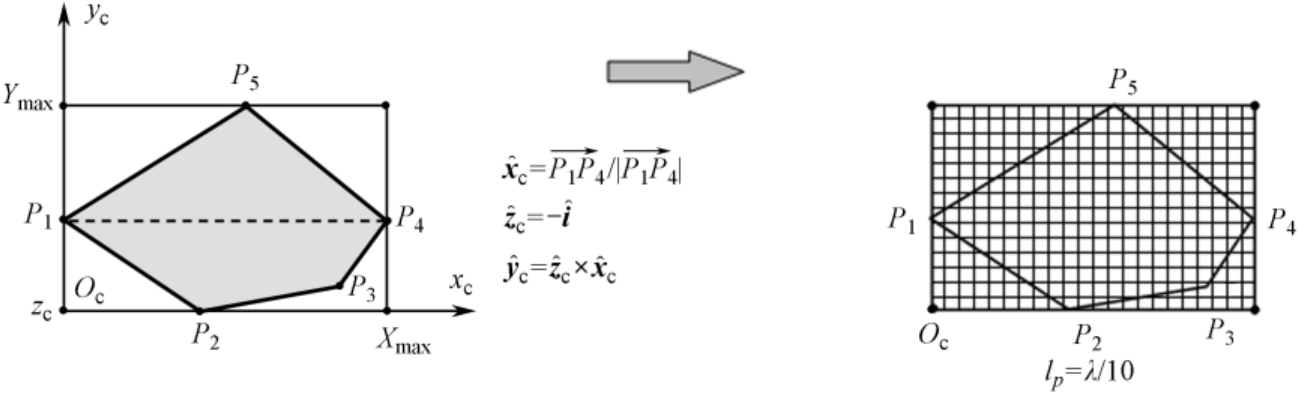
图2.16 射线管的自动划分
(2)
幅度追踪和相位处理
。
确定射线源点后,可以通过快速射线追踪方法准确获得射线在目标内的弹跳路径。对某一射线管而言,一旦射线管各顶点处射线的路径确定后,射线管的弹跳路径也随之确定,然后通过几何光学方法,可以很方便地由入射场强度确定出射线管中心射线在传播过程中的幅度。假定入射平面波(具有
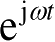 的时间因子)可以表达为
的时间因子)可以表达为
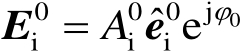
(2.74)
式(2.74)中,
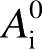 为初始入射电场强度。为简化相位追踪过程,将
为初始入射电场强度。为简化相位追踪过程,将
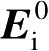 的初始相位分离出来包含在式(2.57)中的相位积分项中,这样由传输路程差造成的入射电场附加相位
φ
0
的初值为
的初始相位分离出来包含在式(2.57)中的相位积分项中,这样由传输路程差造成的入射电场附加相位
φ
0
的初值为
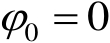
(2.75)
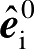 为入射电场极化方向的单位矢量,根据雷达入射波的极化不同而不同,即
为入射电场极化方向的单位矢量,根据雷达入射波的极化不同而不同,即
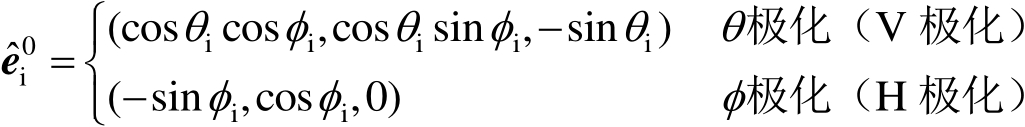
(2.76)
图2.17所示为射线管中心射线在目标的某个三角形面元
S
n
上发生第
i
次反射的示意图。图中
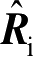 和
和
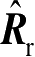 分别为入射方向和反射方向的单位矢量,
分别为入射方向和反射方向的单位矢量,
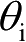 和
θ
r
分别为入射角和反射角,
P
i
和
和
θ
r
分别为入射角和反射角,
P
i
和
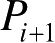 分别为第
i
次和第
i
+1 次反射的反射点,
分别为第
i
次和第
i
+1 次反射的反射点,
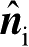 为
S
n
的外法向单位矢量。
为
S
n
的外法向单位矢量。
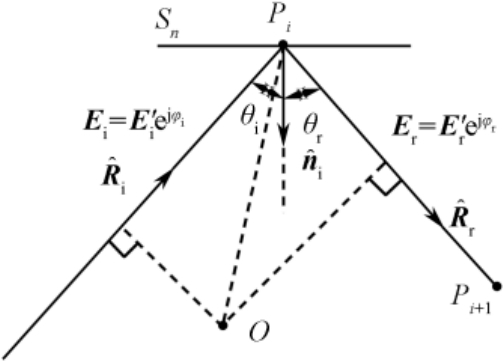
图2.17 射线追踪多次反射示意图
由Snell定理可知
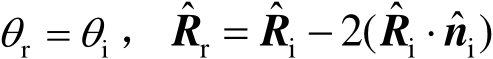
(2.77)
相应地,反射电场矢量
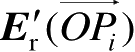 可以由入射电场矢量
可以由入射电场矢量
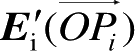 通过下式确定,即
通过下式确定,即

(2.78)
式(2.78)中,
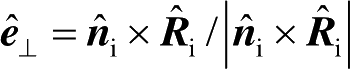 ,
,
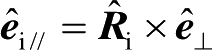 ,
,
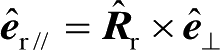 ;
R
//
为入射电场矢量平行于入射面时(平行极化),面元表面的反射系数;
R
⊥
为入射电场矢量垂直于入射面时(重直极化),面元表面的反射系数;(DF)
i
为射线管在
P
i
处的扩散因子,具体计算公式将在后面给出;图2.17中的附加相位
;
R
//
为入射电场矢量平行于入射面时(平行极化),面元表面的反射系数;
R
⊥
为入射电场矢量垂直于入射面时(重直极化),面元表面的反射系数;(DF)
i
为射线管在
P
i
处的扩散因子,具体计算公式将在后面给出;图2.17中的附加相位
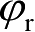 可以表示为
可以表示为
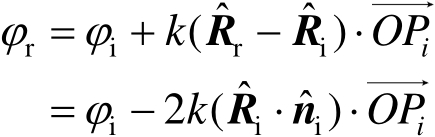
(2.79)
(3)
平面元模型的扩散因子计算
。
对于具有曲面外形的复杂目标,被平面元化后将会缺失诸如曲率之类的重要微分几何信息,而曲面的曲率是场追踪过程中计算射线管扩散因子
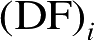 的重要参量,为此,可以采用文献[54]的曲率重构方法获取模型各顶点处的曲率信息。
的重要参量,为此,可以采用文献[54]的曲率重构方法获取模型各顶点处的曲率信息。
模型三角面元上任意点
P
i
(
x
,
y
,
z
)处的曲率可以利用面元顶点处的曲率通过线性插值的方法获得,从而计算出目标表面的曲率矩阵
 。入射波前曲率矩阵
Q
i
则根据入射方向
。入射波前曲率矩阵
Q
i
则根据入射方向
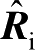 、反射面外法向矢量
、反射面外法向矢量
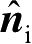 和反射面曲率矩阵
C
建立,然后由
和反射面曲率矩阵
C
建立,然后由
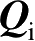 计算反射波前曲率矩阵
计算反射波前曲率矩阵
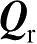 。具体推导可参考文献[58-59],这里仅给出最终的计算表达式。假设
。具体推导可参考文献[58-59],这里仅给出最终的计算表达式。假设
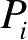 点反射波前曲率矩阵
点反射波前曲率矩阵
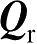 为
为
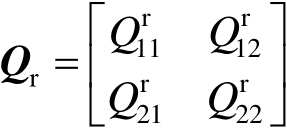
(2.80)
则
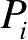 点反射波前的主曲率半径为
点反射波前的主曲率半径为
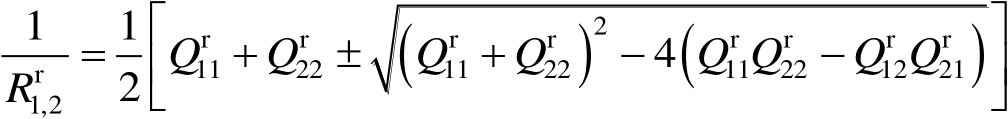
(2.81)
而射线管经过
P
i
所在曲面反射后到达下一个反射点
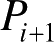 的扩散因子
的扩散因子
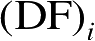 为
为
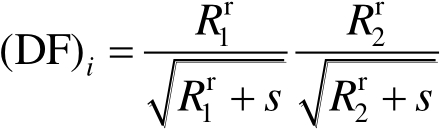
(2.82)
式(2.82)中,
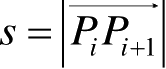 为
为
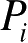 到
P
i
+1
的距离。
到
P
i
+1
的距离。
(4) 射线管多次反射贡献的物理光学积分计算 。 Lee的方法是沿射线管波前利用口面积分 [49] 计算射线管的多次反射贡献。为了尽量减少射线管形状对积分结果的影响,从而提高数值求解的精度,可采用在目标表面对射线管进行物理光学积分的方法计算射线管的多次反射贡献。
利用上述三角形射线管进行射线追踪时,射线管在目标表面的投射区域也为
一系列的三角形区域 S i (射线管焦散为一个点或一条线时除外),这样同样可以利用式(2.57)进行物理光学积分计算出射线管的散射场。值得注意的是,式(2.57)的积分要求在目标表面的照明区域进行,相应地,只有位于目标表面、对接收雷达可见的区域的三角形区域 S i 才能产生多次反射贡献。这一点对于利用物理光学法正确获得目标的多次反射场至关重要。
上述基于面元模型的SBR方法通过追踪射线管在离散面元上的弹跳来解决电磁波与目标的相互作用问题,充分发挥了高频近似方法的局部性优势。理论上,射线密度越高,计算结果就越准确,但随之而来的是计算效率变低,因此这也成为复杂目标散射工程化计算面临的主要挑战。比如,对于大型舰船目标,如果严格按1/10波长来剖分射线管,在X波段(波长3cm)的射线管将有数以亿计,单角度计算时长在10小时以上。海量射线追踪带来的计算量虽然限制了SBR方法的实际应用,但也推动了该方法的发展。当前对算法的优化主要体现在三个方面:一是优化射线管的划分方式,二是精确处理射线管分裂,三是提升射线追踪的效率。
射线管划分方式主要包括前向追踪和后向追踪两种思路,如图2.18所示。前向追踪是在目标外确定射线的路径,图2.16所示即为一种典型的实现方式。后向追踪是在目标表面入射方向可见的面元上确定射线管与面元的交点(如图2.19所示),可以根据目标结构精确定制每一条射线管的尺寸和位置。后向追踪在不考虑射线管分裂的情况下优势明显,其射线数量始终与可见面元数成正比,并且可以避免射线与目标的第一次求交运算,在保证对目标表面的照射区域进行全覆盖的同时不会产生多余射线,进一步结合离散射线等效计算技术 [60] ,通过追踪单根射线和建立等效积分区间来实现对射线场的传播计算,可将舰船类目标的单角度计算时间提升到秒级 [61] 。
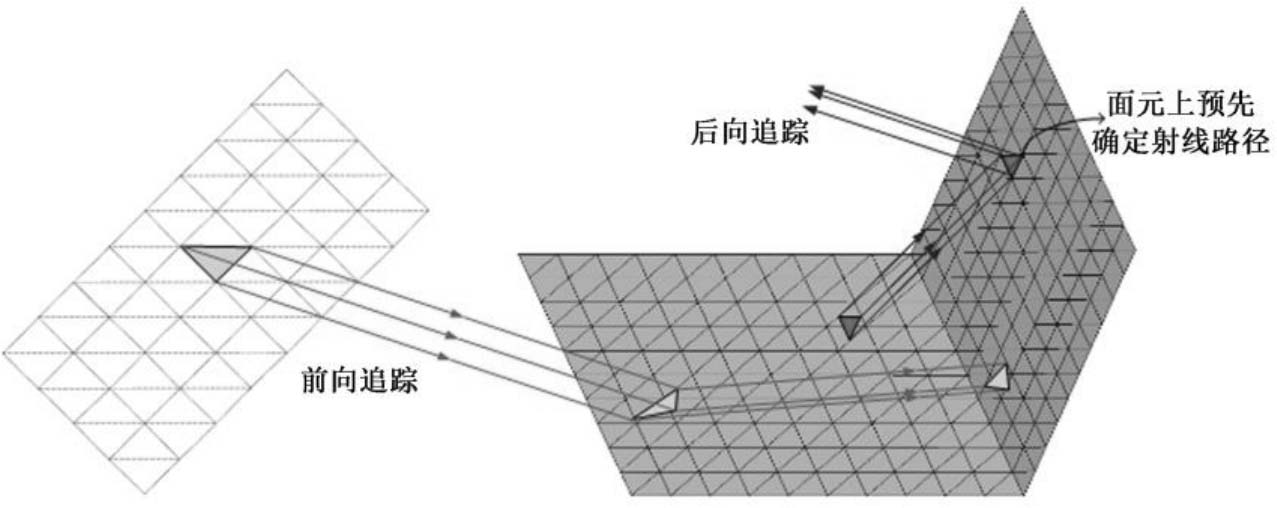
图2.18 两种射线追踪方式
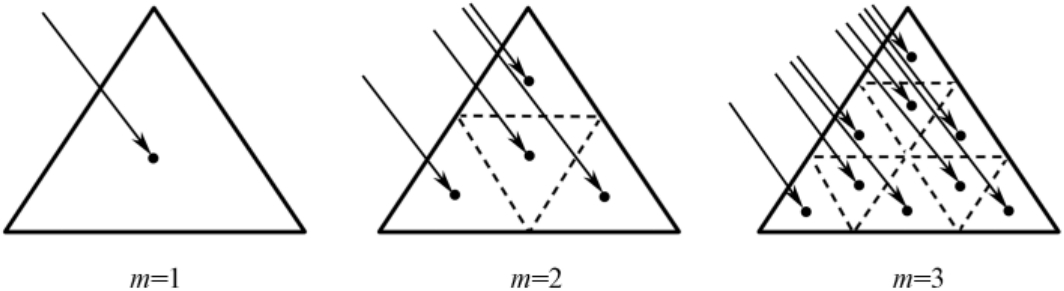
图2.19 可见面元上射线初始化示意图( m 为射线密度控制量)
射线管分裂处理的前提是射线管尺寸不满足1/10波长的密度要求,必须将弹跳后的射线管细分为更多的射线管才能保证计算精度。随着射线管的分裂,追踪的射线数会递增,但对于多尺度非均匀面元模型而言,计算效率优势显著,因为对于大尺寸平板结构而言,适度稀疏的射线密度并不影响计算精度。以基于不规则三角网模型的自适应射线管分裂方法为例 [62] ,总体思路是利用不规则三角网模型动态生成较粗的非均匀初始射线管,经过与模型三角面元求交,进行多边形裁剪和三角化处理,将初始射线管自动分裂成多个子射线管,然后进行迭代计算。
针对平面元模型,射线追踪涉及巨大数量的射线与面元相交运算,常常采用八叉树、K-D树 [63 -64] 等算法,优化和提高射线追踪计算效率。随着GPU硬件能力的显著提升,使得基于NVIDIA OptiX光线追踪引擎的金属与介质复合,甚至以材料为主的目标的复杂动态场景实时射线追踪技术得到长足发展,从而使弹跳射线法日益成熟,并得以在复杂介质目标和动态群目标的高频电磁散射高效求解中得到广泛应用 [65 -66] 。
人们经常用关于未知场量的积分方程来描述电磁散射问题。事实上,许多很好的近似解析和流行的数值方法,如当前用于求解散射问题的矩量法(Method of Moments,MoM),就是建立在这种或那种积分方程基础之上的。
如图2.20所示,考虑受已知电磁场
E
i
,
H
i
照射的具有封闭表面
S
的任意散射体,其入射场可以由
S
外的一些局部源产生,也可以是平面电磁波。一般地,一部分入射场可以到达场点
P
,另一部分在被
S
散射后也可到达场点
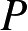 。这样,
P
点处的总场可写成
。这样,
P
点处的总场可写成
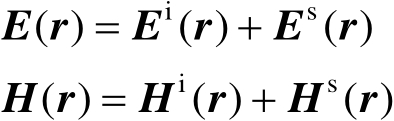
(2.83)
式(2.83)中,
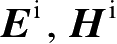 是不存在散射体时的
P
点处的入射电磁场,
是不存在散射体时的
P
点处的入射电磁场,
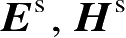 是
P
点处的散射电磁场。
是
P
点处的散射电磁场。
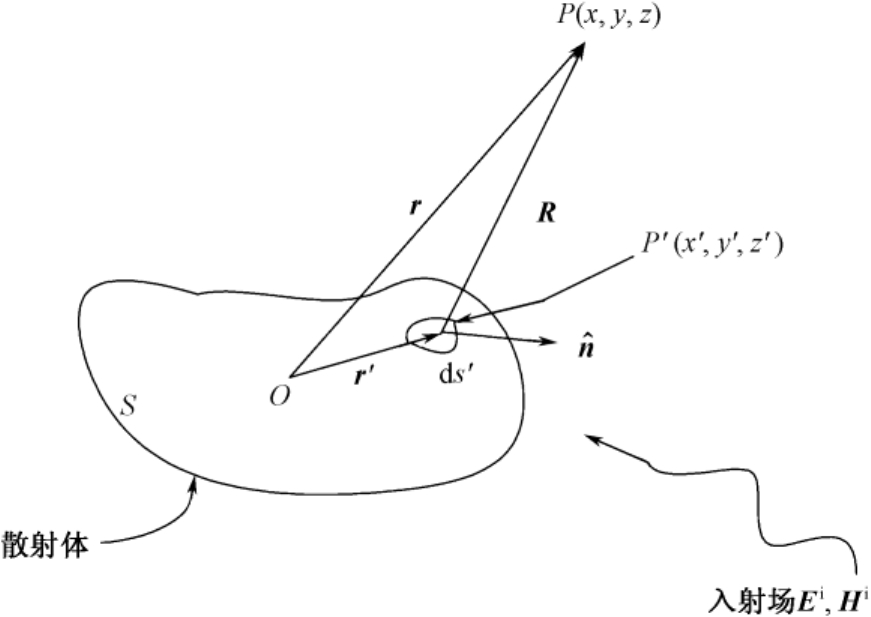
图2.20 散射的几何关系
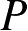 点处的散射场
[67]
可表示为
点处的散射场
[67]
可表示为
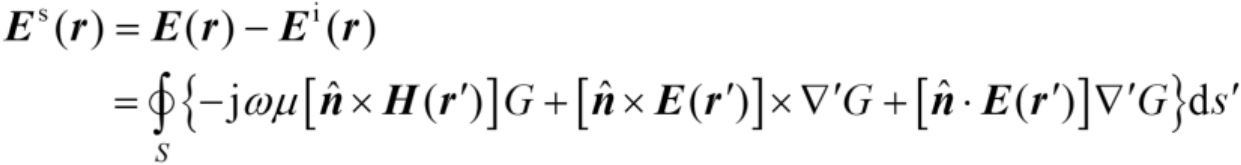
(2.84)
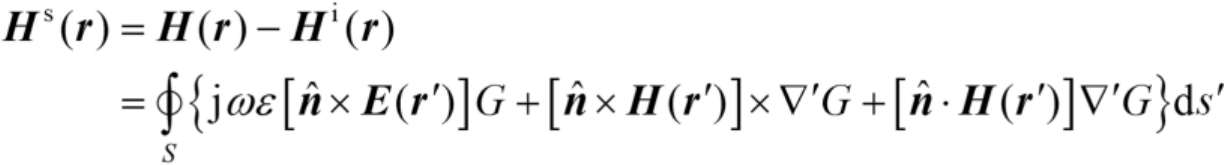
(2.85)
式中,
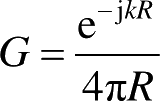 ,
,
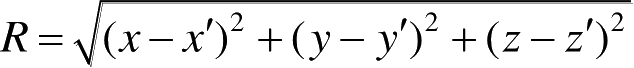 。∇′表示对带撇的坐标进行运算,
。∇′表示对带撇的坐标进行运算,
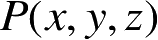 和
P
(
x
′,
y
′,
z
′)分别是场点和源点,所有其他的符号参照图2.20所示的解释。式(2.84)和式(2.85)称为Stratton-Chu方程,它表明散射场完全可由散射体表面上总场的切向和法向分量确定。若散射体是良导体,则在
S
上有
和
P
(
x
′,
y
′,
z
′)分别是场点和源点,所有其他的符号参照图2.20所示的解释。式(2.84)和式(2.85)称为Stratton-Chu方程,它表明散射场完全可由散射体表面上总场的切向和法向分量确定。若散射体是良导体,则在
S
上有
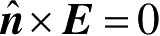 和
和
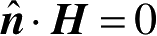 ,式(2.85)表明,要确定
H
s
,仅用
S
上的切向
H
就足够了,但对式(2.84)还是要求知道
S
上的
,式(2.85)表明,要确定
H
s
,仅用
S
上的切向
H
就足够了,但对式(2.84)还是要求知道
S
上的
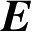 的法向分量。不过,可以利用麦克斯韦方程由
H
s
获得
E
s
,因此,
S
上的
的法向分量。不过,可以利用麦克斯韦方程由
H
s
获得
E
s
,因此,
S
上的
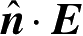 是不必要的。
是不必要的。
在式(2.84)和式(2.85)中,习惯上将表面
S
上的切向电场和磁场分别解释为表面电流和磁流。物理光学近似假定表面场(流)仅仅存在于
 的照明部分,而在其他地方为零,然后通过利用上述方程以及用切平面近似获得的表面场确定散射场。
的照明部分,而在其他地方为零,然后通过利用上述方程以及用切平面近似获得的表面场确定散射场。
1 . 积分方程
对于入射到光滑导体表面上给定的场
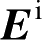 和
和
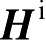 ,感应表面电流
,感应表面电流
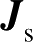 可通过解两个积分方程中的一个来确定。这两个积分方程就是众所周知的电场积分方程(Electric Field Integral Equation,EFIE)和磁场积分方程(Magnetic Field Integral Equation,MFIE)
[68-69]
,可推自Stratton-Chu方程和边界条件
可通过解两个积分方程中的一个来确定。这两个积分方程就是众所周知的电场积分方程(Electric Field Integral Equation,EFIE)和磁场积分方程(Magnetic Field Integral Equation,MFIE)
[68-69]
,可推自Stratton-Chu方程和边界条件
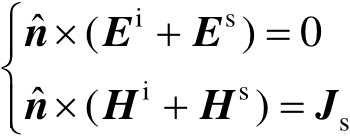
(2.86)
利用电场边界条件、式(2.84)和电流连续性方程,有
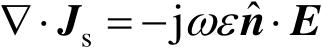
(2.87)
可得EFIE为(以下定义
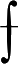 为主值积分号)
为主值积分号)
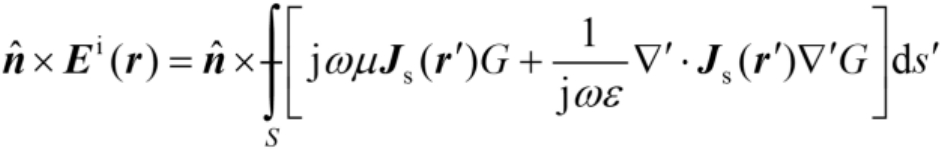
(2.88)
利用磁场边界条件和式(2.85),可得MFIE为
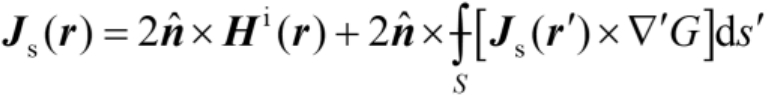
(2.89)
式(2.88)和式(2.89)右边的积分指的是不包括源点和场点重合的那些位置的主值积分。EFIE是第一类积分方程,其中未知电流仅出现在积分内部;而MFIE是第二类积分方程,其中电流既出现在积分的内部,也出现在积分的外部。
除了对应于目标内谐振的一些频率点,EFIE或MFIE都能用来确定表面电流。对于闭合的光滑导体表面,通常使用MFIE。可是,当表面变得很薄(如薄导线和薄圆柱)时,必须使用EFIE,因为此时在MFIE中要恰当地表示
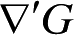 是很困难的。
是很困难的。
当
S
的曲率半径比工作波长大得多时,式(2.89)中
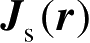 的主要贡献来自右边的第一项,第二项的贡献通常很小。因此,忽略式(2.89)中的第二项,可得在物理光学近似中用到的切平面近似,即
的主要贡献来自右边的第一项,第二项的贡献通常很小。因此,忽略式(2.89)中的第二项,可得在物理光学近似中用到的切平面近似,即
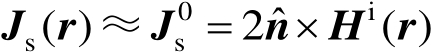
(2.90)
式(2.90)中,
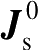 指的是由入射场感应的电流中的均匀部分。后面讨论的物理绕射理论的基础是式(2.89),它的研究重点主要是解析确定由式(2.89)右边第二项产生的电流的非均匀部分。
指的是由入射场感应的电流中的均匀部分。后面讨论的物理绕射理论的基础是式(2.89),它的研究重点主要是解析确定由式(2.89)右边第二项产生的电流的非均匀部分。
2 . 矩量法
对于许多实际的电磁散射和天线问题,所希望的电流分布可以通过数值求解上述积分方程来获得。矩量法(Method of Moments,MoM)是用于这种目的最常用的方法之一。MoM实质上是将积分方程转化为一组代数方程,也就是能用标准的矩阵求逆算法求解的矩阵方程。由于矩量法在Harrington [70] 的经典著作中已详细讨论,因此这里仅简要地概括分析所涉及的基本步骤。
将关于未知电流强度 J s ( r )的MFIE用算子形式写成
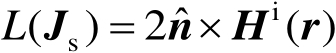
(2.91)
式(2.91)中,右边是已知的, L ( J s )是积分微分线性算子,定义为
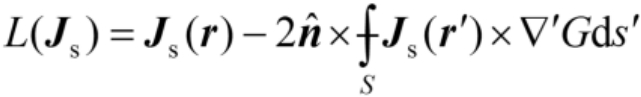
(2.92)
为了简化讨论,下面讨论标量算子方程的求解,即
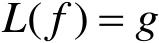
(2.93)
式(2.93)中,
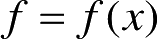 是待确定的未知函数;
g
(
x
)是已知函数;
L
是线性算子。尽管式(2.93)比式(2.91)简单得多,但是求解的基本步骤同样适用于式(2.91)。
是待确定的未知函数;
g
(
x
)是已知函数;
L
是线性算子。尽管式(2.93)比式(2.91)简单得多,但是求解的基本步骤同样适用于式(2.91)。
首先将 f 展开为
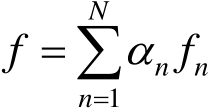
(2.94)
式(2.94)中,
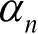 是未知复系数;
f
n
是
x
的已知函数,称为展开函数或基函数。然后将式(2.94)代入式(2.93)中,得
是未知复系数;
f
n
是
x
的已知函数,称为展开函数或基函数。然后将式(2.94)代入式(2.93)中,得
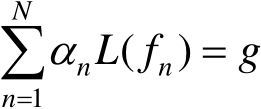
(2.95)
定义在 x 的值域 l 内的内积〈 f , g 〉 为
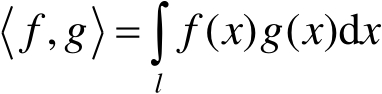
(2.96)
并在值域
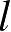 内定义一组权函数或测试函数
w
m
(
m
=1,2,⋯,
N
)。用每一个权函数
w
m
与式(2.95)做内积可得
内定义一组权函数或测试函数
w
m
(
m
=1,2,⋯,
N
)。用每一个权函数
w
m
与式(2.95)做内积可得
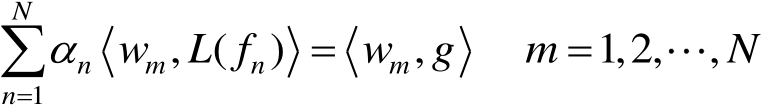
(2.97)
将式(2.97)给出的代数方程组写成矩阵形式为
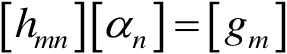
(2.98)
式(2.98)中
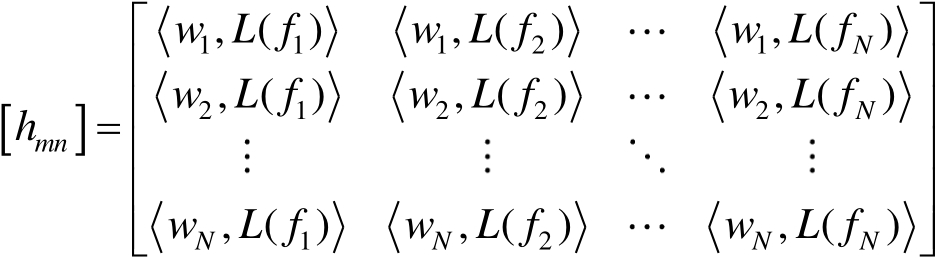
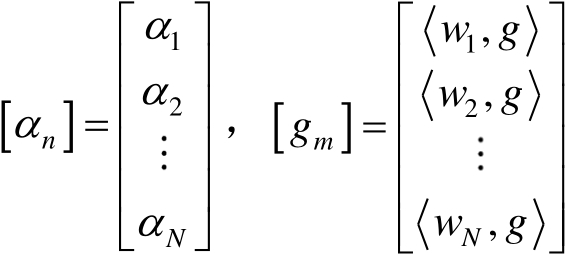
假定[ h mn ] 是非奇异的,由式(2.98)利用标准的矩阵求逆算法确定[ α n ],即
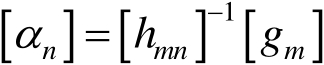
(2.99)
最后便可利用式(2.94)确定未知函数
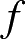 。
。
上面假定了基函数和权函数是不同的。如果两个函数是相同的,则相应的解称为伽辽金(Galerkin)解。
尽管上面归纳的数值方法是直接的,可是,由于涉及矩阵求逆的要求,可处理问题的尺寸严重受限于计算机的能力。一般认为,单纯的MoM最多只能提供具有几个至数十个波长尺寸的目标的散射解。为拓展MoM处理电大尺寸目标散射问题的能力,可以考虑将MoM与其他一些快速算法结合起来使用,如多层快速多极子算法 [71-72] (Multilevel Fast Multipole Algorithm)。
另一种不用边缘绕射系数或一致性渐近展开的用于求解与散射计算有关的边缘不连续问题的方法是由Ufimtsev提出的物理绕射理论(Physical Theory of Diffraction,PTD)。在文献[73-74]中可以找到对PTD的概述。Ufimtsev发现,导体表面上的表面总电流等于下面两种电流之和
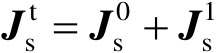
(2.100)
式(2.100)中,
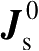 是式(2.90)讨论的物理光学电流,称为总电流的一致性部分;
是式(2.90)讨论的物理光学电流,称为总电流的一致性部分;
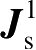 是边缘电流或由某些形式的不连续性导致的电流的非一致性部分。
是边缘电流或由某些形式的不连续性导致的电流的非一致性部分。
一旦求得
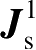 ,
,
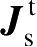 就构成了对精确的表面总电流比
就构成了对精确的表面总电流比
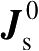 更好的近似,于是得到比单独用物理光学近似更准确的结果。用PTD近似的优点是,对给定的有限总电流,场在包含入射和反射阴影边界以及焦散处的任何一处都是有限的。这种方法的缺点是,对劈绕射,需要计算
更好的近似,于是得到比单独用物理光学近似更准确的结果。用PTD近似的优点是,对给定的有限总电流,场在包含入射和反射阴影边界以及焦散处的任何一处都是有限的。这种方法的缺点是,对劈绕射,需要计算
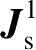 及其产生的场。边缘场
E
1
通常表示为
及其产生的场。边缘场
E
1
通常表示为
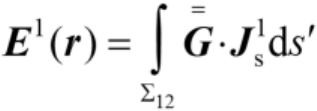
(2.101)
式(2.101)中,Σ
12
是与产生
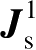 有关的表面;
有关的表面;
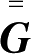 是与几何结构有关的并矢格林函数。
是与几何结构有关的并矢格林函数。
在场计算当中,Ufimtsev仅用了阶数为
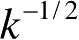 的主要项
[75]
。一般来说,确定
的主要项
[75]
。一般来说,确定
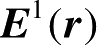 是很棘手的,这里不予讨论。
是很棘手的,这里不予讨论。
迄今为止,已经讨论了多种求解电磁散射问题的高频近似解析方法,描述了用于获得大量散射问题数值解的一种普遍的数值方法——矩量法。这些方法中的每一种都有其应用范围及优缺点。混合法(Hybrid Method,HM)通常将一种方法的优点与另一种方法的优点组合起来以便有效地确定问题的解。一些学者已经提出了多种类似的方法 [21,76] ,这里仅简要介绍其中的两种。
MoM常用于电尺寸不太大的目标,而GTD一般可对尺寸比1个波长大得多的目标给出好的结果,因此,可以将这两种方法组合使用,以有效求解中等尺寸或尺寸在谐振区或超过谐振区的目标的辐射和散射问题。文献[76]提出的MoM和GTD方法组合确定了与辐射或散射问题有关的阻抗矩阵。矩量法通常得到光滑表面的阻抗矩阵,但当光滑表面包含某些不连续性时,一般利用GO和GTD对MoM矩阵进行修正。文献[76]给出了该方法的细节,其对诸如在导体圆盘中心上的单极子、接近导体劈的单极子,以及在四边或八边形导体板中心处的单极子之类的天线获得了较好的结果。文献[21]则通过以另一种形式组合GTD和MoM来获得电磁散射问题的数值解。文献[77]组合Fock理论和MoM求解多表面阻抗加载凸导体柱的电磁散射。文献[78]讨论了组合PO、PTD、Fock理论和MoM的混合法在导体目标、部分或完全涂覆目标中的应用。可是,不像MoM,混合法应用于RCS问题时与具体的目标几何结构有关,因此没有专门的结果适用于所有目标。
下面将通过考虑如图2.21所示的直角导体劈结构对平面波的散射来描述这种方法。在这种方法中 [76] ,其边缘周围要求用MoM电流,GTD场在一些点上进行匹配,由此充分减小了要求解的MoM电流样本的数量。这种程序产生了一组联立方程,通过求解该方程组,可以得到MoM电流的复幅度和GTD的数值系数。
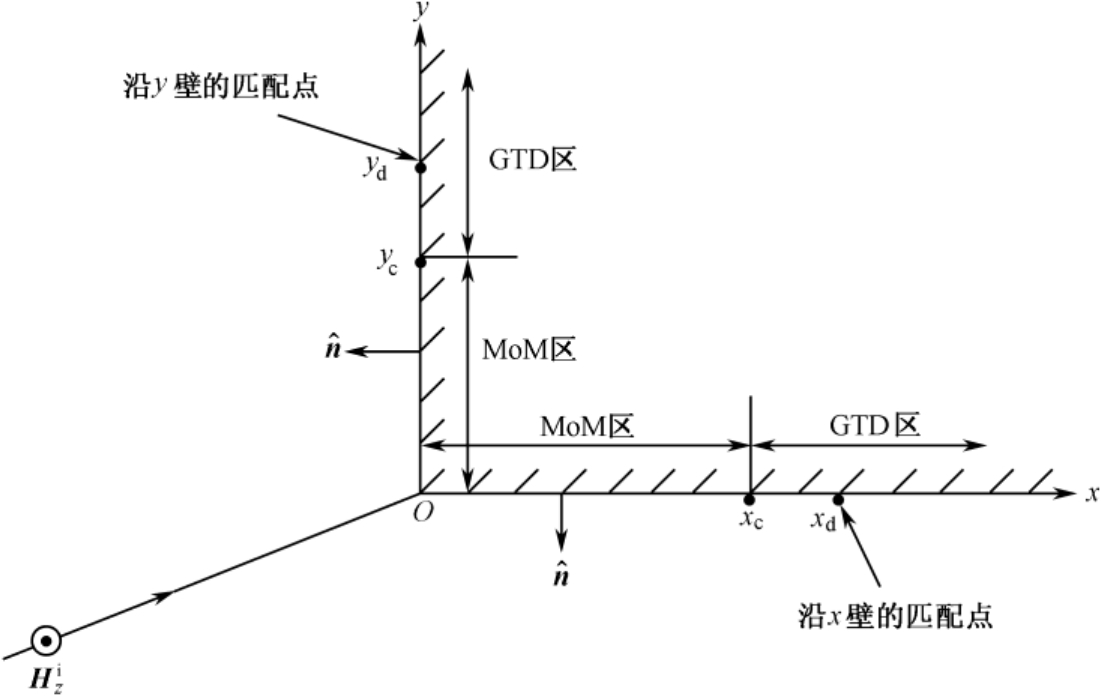
图2.21 直角导体劈对平面波散射的几何关系
考虑磁场沿
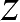 方向极化的平面波入射到如图2.21所示的直角导体劈上。在GTD近似下,劈表面的总电流为
方向极化的平面波入射到如图2.21所示的直角导体劈上。在GTD近似下,劈表面的总电流为
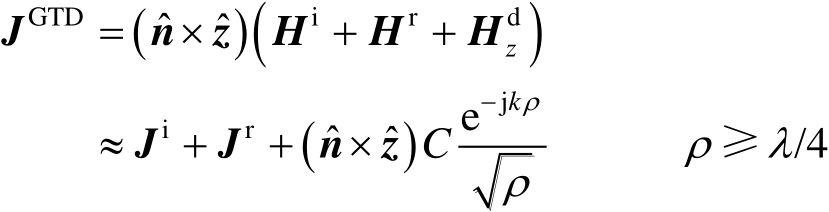
(2.102)
式(2.102)中,
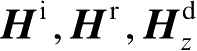 分别是劈表面上的入射、反射和绕射磁场;
分别是劈表面上的入射、反射和绕射磁场;
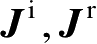 分别是由磁场的入射和反射部分产生的表面电流;
C
是待确定的未知常数,在目前的情况下代表绕射系数
D
x
和
D
y
;其他参数如图2.21所示。
分别是由磁场的入射和反射部分产生的表面电流;
C
是待确定的未知常数,在目前的情况下代表绕射系数
D
x
和
D
y
;其他参数如图2.21所示。
关于表面总电流适合的MFIE [70] 为
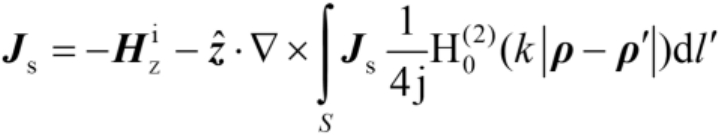
(2.103)
式(2.103)中,
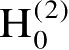 是第二类零阶汉开尔函数。表面总电流假定为如下分量形式
是第二类零阶汉开尔函数。表面总电流假定为如下分量形式
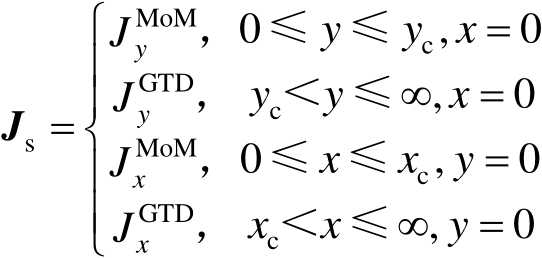
(2.104)
从式(2.104)中可以看出,用MoM获得的电流在0≤ x ≤ x c 和0≤ y ≤ y c 范围内,式(2.102)给出的GTD电流在远离绕射边缘的地方(也即在这两个区域之外)是有效的。
现在,边缘周围电流的MoM分量可由简单的基函数确定,即
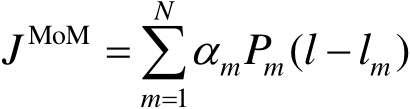
(2.105)
式(2.105)中,
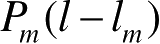 是以
α
m
为展开系数的正交脉冲函数。利用点配置,得到一组联立方程为
是以
α
m
为展开系数的正交脉冲函数。利用点配置,得到一组联立方程为
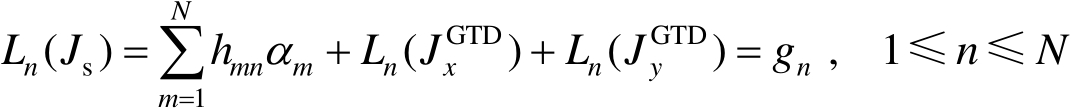
(2.106)
式(2.106)中,
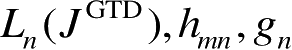 在文献[76]中给出。
在文献[76]中给出。
为了确定分别与
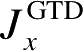 和
和
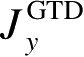 有关的两个绕射系数
D
x
和
D
y
[在式(2.102)中用
C
表示],需要选择两个另外的匹配点,如图2.21中的(
x
d
,0)和(0,
y
d
),它们都在GTD区域,因而产生了与式(2.106)类似的另外两个方程。在这种方式下,对
N
+2 个未知数获得了
N
+2 个方程[式(2.106)中
N
个电流脉冲系数加上两个绕射系数]。
有关的两个绕射系数
D
x
和
D
y
[在式(2.102)中用
C
表示],需要选择两个另外的匹配点,如图2.21中的(
x
d
,0)和(0,
y
d
),它们都在GTD区域,因而产生了与式(2.106)类似的另外两个方程。在这种方式下,对
N
+2 个未知数获得了
N
+2 个方程[式(2.106)中
N
个电流脉冲系数加上两个绕射系数]。
1. 时间步进法
尽管频域积分方程可以通过矩阵求逆或迭代方法来求解,然而,时域积分方程由于具有时间滞后的特点使其可以通过更直接的方法进行求解 [79] 。对于实导体目标,时域积分方程为
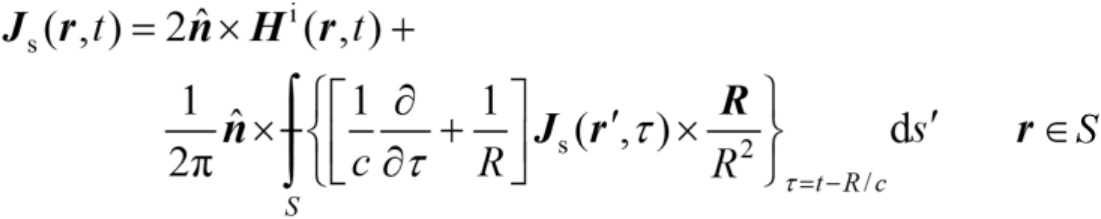
(2.107)
式(2.107)中,
r
′和
r
分别是从坐标原点到积分点和观察点的位置矢量;
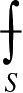 表示柯西主值积分;
表示柯西主值积分;
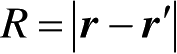 ,
,
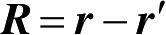 ;
;
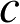 为光速;
t
为时间;
为光速;
t
为时间;
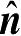 是在
r
处的单位法向矢量;
是在
r
处的单位法向矢量;
 为目标的表面;
为目标的表面;
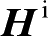 为入射磁场;
J
s
为表面电流密度。
为入射磁场;
J
s
为表面电流密度。
式(2.107)的首项给出了众所周知的物理光学电流,积分项表示在表面其他点上的电流对
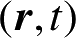 处电流的影响。这里关键的一点是积分内的电流
J
s
比时间
t
滞后
R
/
c
。由于
R
=0 的点在主值积分中已经排除,所以
R
/
c
不会为零,这样,
τ
总是小于
t
。由式(2.107)不难看出,未知电流相当于已知的物理光学项与由已知的
J
s
的历史值构成的积分项的和,这种特点便构成了用所谓的时间步进法(Marching-on-in-Time Method,MTM)的迭代方法求解时域积分方程的基础。在因果关系假设的前提下,所有的电流和场在
t
<0时都为零。
P
点处的电流
J
s
可以按时间步进直接计算,从时刻
t
=0 开始,直到所要求的时间
t
为止。计算是直接的但又是迭代的,在
t
=
t
1
,
t
2
,⋯ 时刻上进行。这种程序其实是下三角矩阵方程的递归解,即不需要复矩阵求逆的简单直接的矩量法。
处电流的影响。这里关键的一点是积分内的电流
J
s
比时间
t
滞后
R
/
c
。由于
R
=0 的点在主值积分中已经排除,所以
R
/
c
不会为零,这样,
τ
总是小于
t
。由式(2.107)不难看出,未知电流相当于已知的物理光学项与由已知的
J
s
的历史值构成的积分项的和,这种特点便构成了用所谓的时间步进法(Marching-on-in-Time Method,MTM)的迭代方法求解时域积分方程的基础。在因果关系假设的前提下,所有的电流和场在
t
<0时都为零。
P
点处的电流
J
s
可以按时间步进直接计算,从时刻
t
=0 开始,直到所要求的时间
t
为止。计算是直接的但又是迭代的,在
t
=
t
1
,
t
2
,⋯ 时刻上进行。这种程序其实是下三角矩阵方程的递归解,即不需要复矩阵求逆的简单直接的矩量法。
一旦获得了电流密度,就能计算出空间任一点处的场以及双站RCS。例如,区散射场为
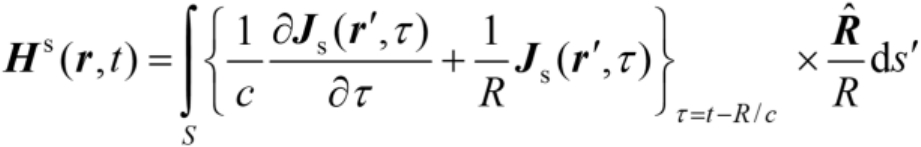
(2.108)
对入射场和散射场做傅里叶变换后可得RCS。
2. 时域有限差分法
时域有限差分(Finite Difference Time Domain,FDTD)法是由K. S. Yee
[80]
于1966年首次提出的一种直接求解时域麦克斯韦旋度方程的电磁场数值计算方法。具体地说,对电磁场(
E
,
H
)分量在空间和时间上采取交替抽样的离散方式,每一个
 (或
H
)场分量周围有4个
H
(或
E
)场分量环绕,应用这种后来被称为Yee元胞(如图2.22所示)的离散方式,对电场和磁场的空间和时间导数采用简单的二阶中心差分近似,可将含时间变量的麦克斯韦旋度方程转化为一组差分方程,由电磁问题的初始值和边界条件就可以在时间轴上逐步推进地求解空间电磁场分布。计算中只要将空间某一样本点的电场(或磁场)与周围各点的磁场(或电场)直接相关联,且将相应的材料参数赋值于空间每一个元胞,使得FDTD法可以统一地处理具有复杂形状和包含不均匀材料的体目标的电磁散射问题。
(或
H
)场分量周围有4个
H
(或
E
)场分量环绕,应用这种后来被称为Yee元胞(如图2.22所示)的离散方式,对电场和磁场的空间和时间导数采用简单的二阶中心差分近似,可将含时间变量的麦克斯韦旋度方程转化为一组差分方程,由电磁问题的初始值和边界条件就可以在时间轴上逐步推进地求解空间电磁场分布。计算中只要将空间某一样本点的电场(或磁场)与周围各点的磁场(或电场)直接相关联,且将相应的材料参数赋值于空间每一个元胞,使得FDTD法可以统一地处理具有复杂形状和包含不均匀材料的体目标的电磁散射问题。
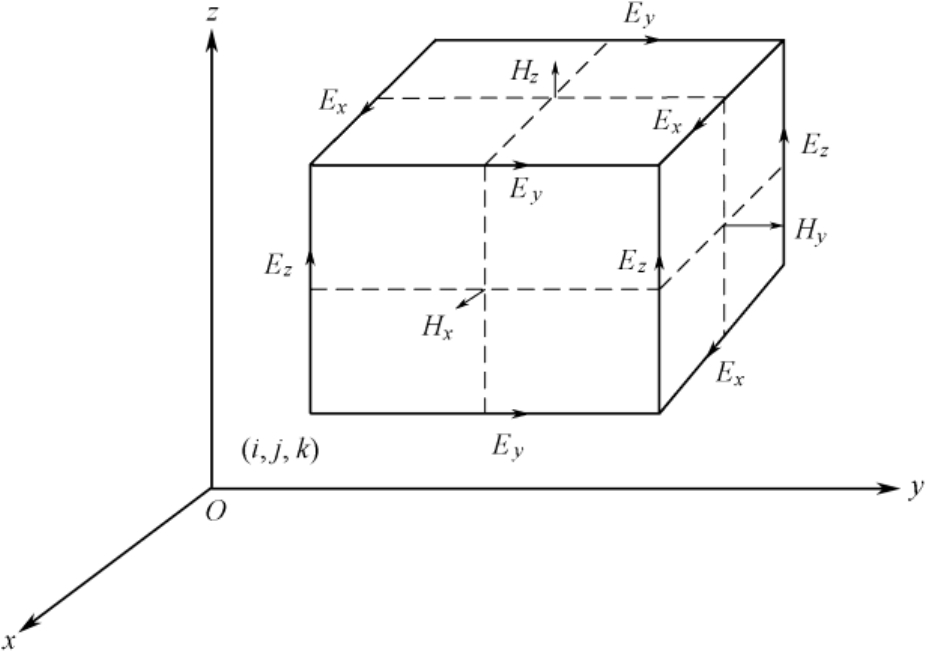
图2.22 Yee元胞
表2.7列出了在笛卡儿坐标系中构成麦克斯韦方程的6个电磁场旋度方程。表2.8列出了对在离散时间步上和在离散元胞位置上采样的场矢量分量所假定的时-空符号,表示对麦克斯韦方程的空间和时间偏导数的中心差分近似。表2.9提供了时间步场矢量分量的有限差分表达式的例子。不难发现,每一个时间步表达式的右边的所有量都是已知的(存储在计算机内存中),因此表达式完全是显式的,可以在时间上迭代求解,不需要矩阵求逆运算。
表2.7 在笛卡儿坐标系中构成麦克斯韦方程的6个电磁场旋度方程
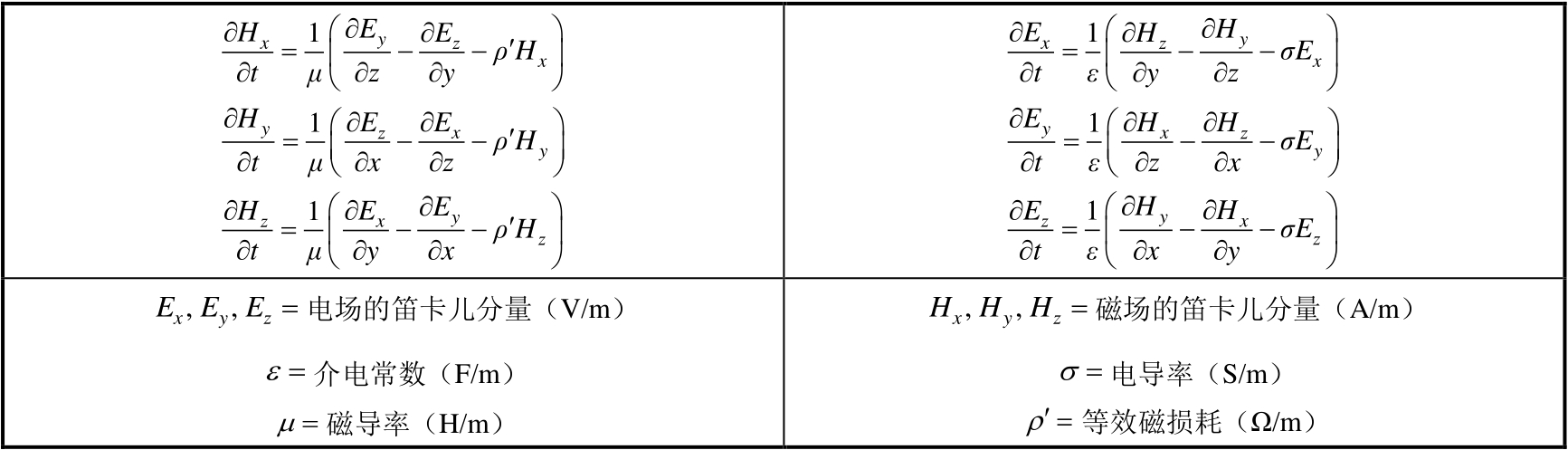
表2.8 对麦克斯韦方程的空间和时间偏导数的中心差分近似

表2.9 时间步场矢量分量的有限差分表达式的例子

由于准确性和算法稳定性的原因,要求适当选择
 和
和
 。为了保证计算的电磁场的空间导数的准确性,
δ
必须比波长小。
δ
≤
λ
/10 足以实现由空间导数近似所导致的近场FDTD解的不确定性小于±7
%
(±0.6dB)
[81]
。对
δ
≤
λ
/20,这种不确定性下降到小于
。为了保证计算的电磁场的空间导数的准确性,
δ
必须比波长小。
δ
≤
λ
/10 足以实现由空间导数近似所导致的近场FDTD解的不确定性小于±7
%
(±0.6dB)
[81]
。对
δ
≤
λ
/20,这种不确定性下降到小于
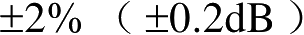 。
。
为了保证以表2.7为例的时间步进算法的稳定性,
 选择满足下面的不等式
[81]
选择满足下面的不等式
[81]
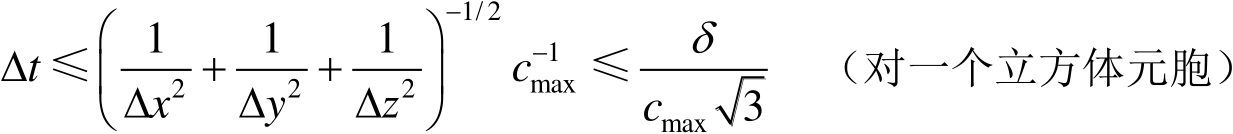
(2.109)
式(2.109)中, c max 是模型内最大的波相速。
FDTD方法将计算区域划分为总场区和散射场区,如图2.23(a)所示。这种划分是很有用的,因为它允许在总场区对任意入射角、极化、时域波形和持续时间 [82-83] 的入射平面波进行有效模拟。
这种划分可以带来如下三个额外的好处:
1)大的近场计算动态范围
由于感兴趣的目标放在总场区,因此直接计算在屏蔽区域或屏蔽物内的低总场电平不会遭受减法噪声(在这样的区域中,时间步进的散射场与对消的入射场相加而获得低的总场电平就会产生减法噪声)。避免减法噪声是获得超过60dB近场计算动态范围的关键 [81] 。
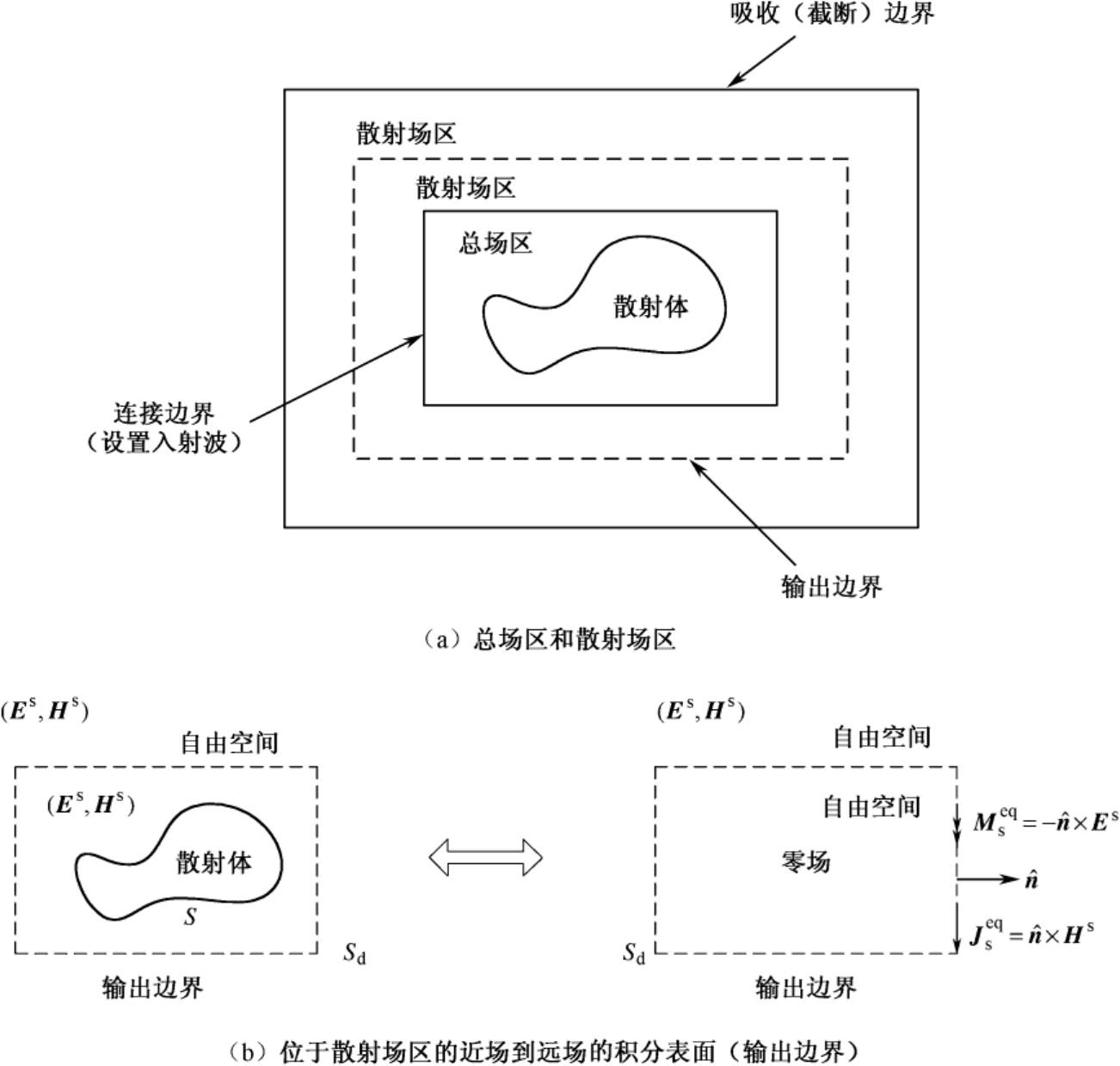
图2.23 FDTD区域的划分
2)自然满足电磁边界条件
将目标放在总场区保证了自然满足穿过介质界面时切向场的连续性,而无须对每种具体的目标沿着复杂介质界面上成千上万个点分别计算入射场。如图2.23(a)所示,这种分区安排要求入射场的计算仅沿着总场区和散射场区之间的矩形连接表面进行。这个表面是固定的,与包围的待模化目标的形状和组成无关。因此,在计算机的运行时间方面获得了得益,这种得益随目标的复杂性增加而增加。
3)双站RCS的系统计算
在图2.23中,在散射场区通过选择合适的FDTD网格可以很容易地由近场求得远场,该网格也就是输出边界,如图2.23中的虚线所示。在这个虚拟表面上对由FDTD方法计算的切向散射
 和
H
场用自由空间格林函数进行加权并积分,可以得到远场响应和双站的RCS
[83-85]
。近场积分表面是一个固定的矩形,因此与包围的待模化目标的形状和组成无关。
和
H
场用自由空间格林函数进行加权并积分,可以得到远场响应和双站的RCS
[83-85]
。近场积分表面是一个固定的矩形,因此与包围的待模化目标的形状和组成无关。
图2.23(a)用“截断边界”表示包围散射区的最外层的矩形表面。由于在截断边界外侧场的数据是未知的,因此,在这些平面上的场不能用前面讨论的中心差分法进行计算。可是,这些数据需要形成中心差分,故必须引入辅助的截断边界条件(又称吸收边界条件),而这一条件又必须满足麦克斯韦方程,即入射到截断边界上的外行散射波应该穿过截断边界而无明显的非物理反射,就好像截断边界是无形的。
上面要求的吸收边界条件其实就是近场区的辐射条件 [86-88] 。从简单的插值边界开始,至今已经发展了多种吸收边界条件。目前比较广泛采用的有Mur吸收边界 [82] ,以及完全匹配层(Perfectly Matched Layer,PML)吸收边界条件 [89-91] 。
用FDTD方法计算目标的散射问题所需要的计算机存储量正比于待模化的体积中的电磁场未知量的个数
N
,因此当
 值很大时,该方法要受计算机存储量和计算时间的限制。可是,如果仔细观察表2.7所示的方程,就会发现FDTD方法具有局域性的特点,即只与上一时刻以及周围空间的场有关,故FDTD方法特别适合并行计算。将FDTD区域分割成若干个子区域分别进行计算,各个子区域只需在边界处与相邻的其他子区域进行切向场值的数据交换,就可以使整个迭代计算进行下去,从而实现对电大尺寸目标FDTD的计算
[92]
。
值很大时,该方法要受计算机存储量和计算时间的限制。可是,如果仔细观察表2.7所示的方程,就会发现FDTD方法具有局域性的特点,即只与上一时刻以及周围空间的场有关,故FDTD方法特别适合并行计算。将FDTD区域分割成若干个子区域分别进行计算,各个子区域只需在边界处与相邻的其他子区域进行切向场值的数据交换,就可以使整个迭代计算进行下去,从而实现对电大尺寸目标FDTD的计算
[92]
。
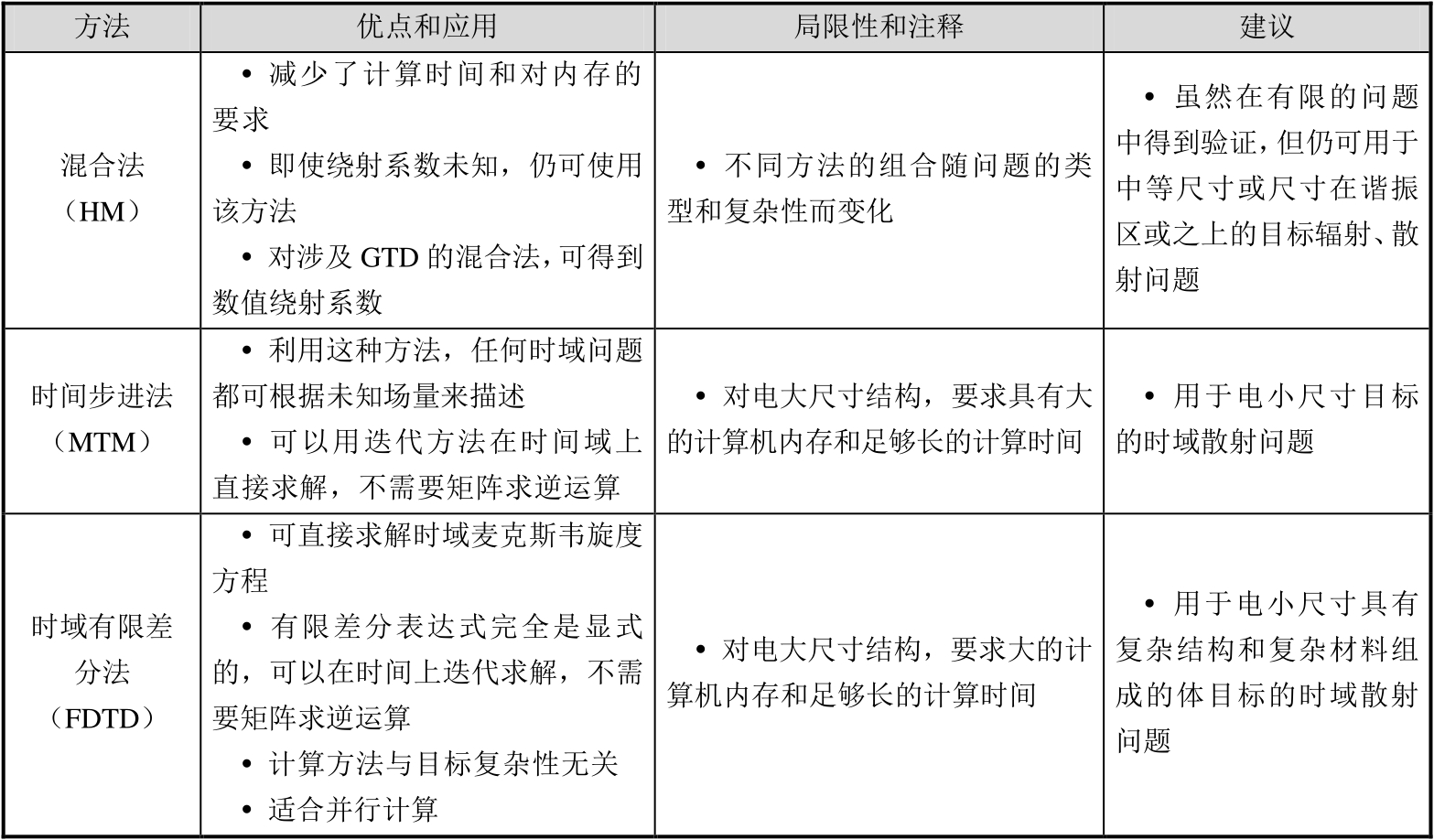
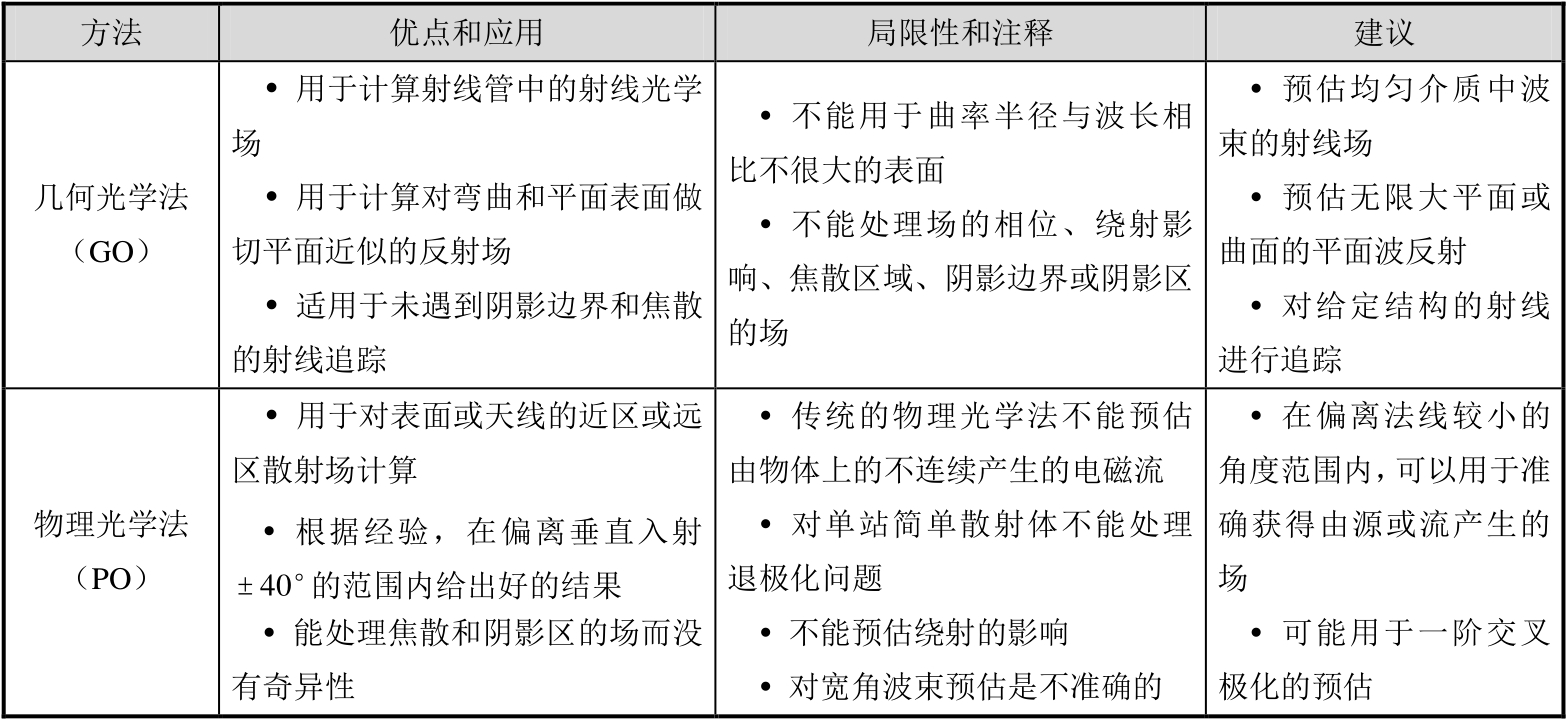
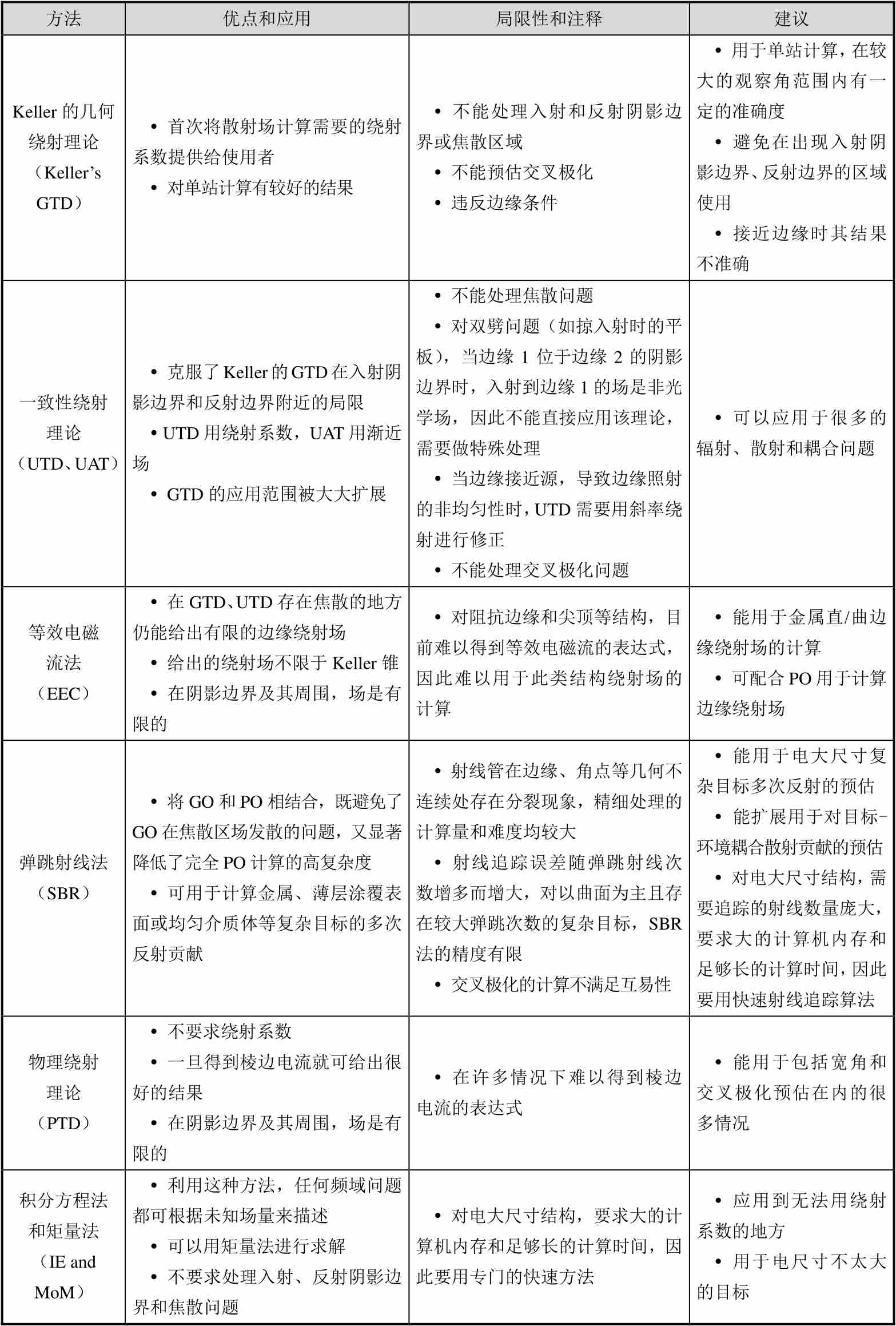
前面各节讨论了RCS预估的不同方法及其应用,虽然对一个给定的实际问题,根据前面各节的讨论,具体选择什么方法是很清楚的,但是,为了方便起见,下面还是以表格的形式对这些方法的优缺点、应用范围和局限性进行归纳,如表2.10所示。
表2.10 RCS预估方法的比较
续表
续表