




RCS(雷达散射截面,简称为散射截面),度量了雷达目标对照射电磁波的散射能力。
对RCS的定义有两种观点:一种是基于电磁散射理论的观点,另一种是基于雷达测量的观点,但两者的基本概念是统一的,均定义为:单位立体角内目标朝接收方向散射的功率与从给定方向入射于该目标的平面波功率密度之比的4π 倍。
基于电磁散射理论的观点解释为 [1-2] :雷达目标散射的电磁能量可以表示为目标的等效面积与入射功率密度的乘积,它是基于在平面电磁波照射下,目标散射具有各向同性的假设。对于这样一种平面波,其入射功率密度为
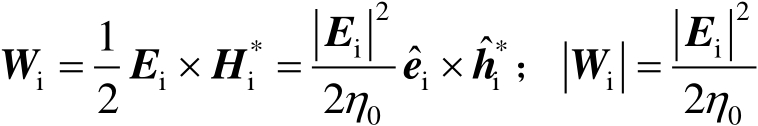
(2.1)
式中,
E
i
和
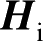 分别为入射电场强度与磁场强度;“*”表示复共轭;
分别为入射电场强度与磁场强度;“*”表示复共轭;
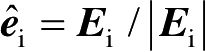 ;
;
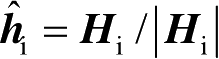 ;
η
0
=377Ω 为自由空间波阻抗。
;
η
0
=377Ω 为自由空间波阻抗。
借鉴天线口径有效面积的概念,目标截取的总功率为入射功率密度与目标等效面积 σ 的乘积,即
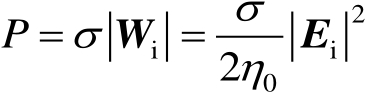
(2.2)
假设功率是各向同性且均匀地向四周立体角散射,则在距离目标 R 处的目标散射功率密度为
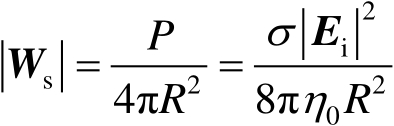
(2.3)
然而,类似于式(2.1),散射功率密度又可用散射场强 E s 来表示,即
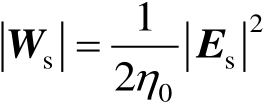
(2.4)
由式(2.3)与式(2.4)得
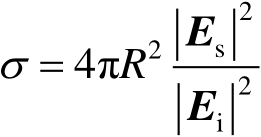
(2.5)
式(2.5)符合RCS的定义。当距离
R
足够远时,照射目标的入射波近似为平面波,这时
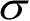 与
R
无关(因为散射场强
E
s
与
R
成反比、与
E
i
成正比),因而定义远场RCS时,
R
应趋向无限大,即要满足远场条件。
与
R
无关(因为散射场强
E
s
与
R
成反比、与
E
i
成正比),因而定义远场RCS时,
R
应趋向无限大,即要满足远场条件。
根据电场与磁场的储能互相可转换的原理,远场RCS的表达式应为
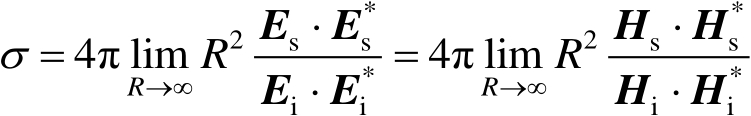
(2.6)
基于雷达测量观点定义的RCS是由雷达方程式推导出来的。雷达系统由发射机、发射天线到目标的传播途径、目标、目标到接收天线的传播途径,以及接收机等几部分组成。由雷达方程式推导出的接收功率的表达式为
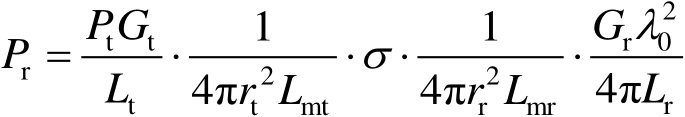
(2.7)
式(2.7)中, P r 为接收机输入端功率(W); P t 为发射机功率(W); G r , G t 分别为接收天线与发射天线的增益(无因次); L t , L mt 分别为发射机内馈线与发射天线到目标传播途径的损耗(无因次); L r , L mr 分别为接收机内馈线与目标到接收天线传播途径的损耗(无因次); σ 为目标散射截面(m 2 ); r t , r r 分别为发射天线到目标与目标到接收天线的距离(m),当单站(收与发同一地点)时, r t = r r ; λ 0 为雷达工作波长。
当忽略各种损耗,即 L t , L mt , L r , L mr 均为1时,式(2.7)简化为
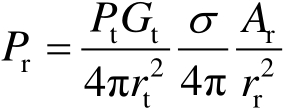
(2.8)
式(2.8)中,
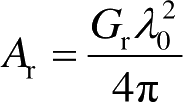 为接收天线有效面积(m
2
)。式(2.8)的物理概念是:右边第一分式为目标处的照射功率密度(W/m
2
),前两分式乘积为目标各向同性散射功率密度(W/球面rad);右边第三分式为接收天线有效口径所张的立体角。式(2.8)还可整理为
为接收天线有效面积(m
2
)。式(2.8)的物理概念是:右边第一分式为目标处的照射功率密度(W/m
2
),前两分式乘积为目标各向同性散射功率密度(W/球面rad);右边第三分式为接收天线有效口径所张的立体角。式(2.8)还可整理为
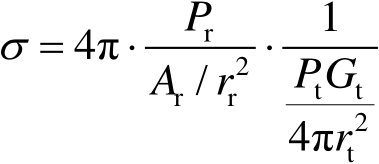
=4π⋅ [接收天线所张立体角内的散射功率(W)]/
[目标处照射功率密度(W/单位面积)]
(2.9)
式(2.9)就是基于雷达测量观点由雷达方程式导出来的,它与基于电磁散射理论得出的RCS定义[式(2.6)]是一致的。式(2.6)适用于理论计算,而式(2.9)适用于用相对标定法来测量目标RCS。将待测目标和已知精确RCS值的定标体轮换置于同一距离上,当测量雷达的威力系数(即
P
t
,
G
t
与
A
r
均不变)相同时,分别测得接收功率
P
r
与
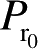 ,则
,则
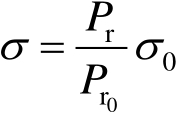
(2.10a)
式(2.10a)中, σ 0 的下标0表示定标体的RCS值,因此目标RCS值与 r t , r r 无关。
RCS的量纲是面积单位,可是它与实际目标的物理面积几乎没有关系,因此不主张将RCS称为雷达截面积。RCS常用单位是m
2
,通常用符号
σ
表示。为了归一化地表示各类目标RCS随波长的变化关系,归一化RCS曲线图的纵坐标为
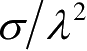 ,横坐标为
k
a
=2π
a
/
λ
(
a
为目标特征尺寸),因此这时两维坐标都无因次。又由于目标RCS变化的动态范围很大,常用其相对于1m
2
的分贝数来表达,即分贝平方米,符号为dBm
2
,表示为
,横坐标为
k
a
=2π
a
/
λ
(
a
为目标特征尺寸),因此这时两维坐标都无因次。又由于目标RCS变化的动态范围很大,常用其相对于1m
2
的分贝数来表达,即分贝平方米,符号为dBm
2
,表示为
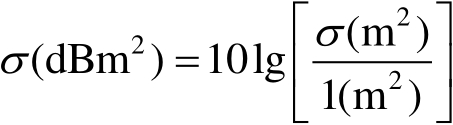
(2.10b)
从广义上来说,在不满足远场条件下,即不满足平面波照射与接收状态下,测量得到的RCS值会与测量距离有关,这时可引出近场RCS的定义。
在常规雷达中,目标散射的雷达回波频率等于雷达发射频率。可是在宽带高分辨雷达中,目标照射波不是单色波,而且频谱很宽,由于目标对照射频谱内各频率分量的响应不同,其散射回波的谱分布特性与发射谱分布有较大差别,因此为了研究并表征在任意照射谱下目标散射特性,需要引入时域的目标冲激响应概念,并通过它来定义宽带RCS。
学者凯纳夫(Kennaugh)于1958年首先提出目标冲激响应的概念 [3-4] 。如图2.1所示。
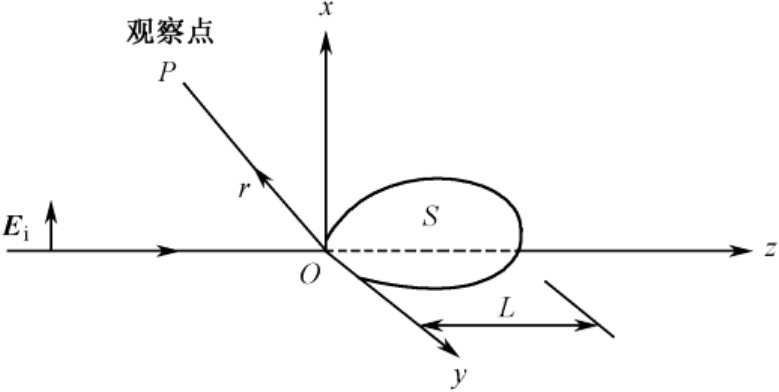
图2.1 冲激平面波照射目标
入射平面波为
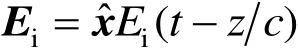
(2.11)
式中, c 为光速, t 为时间, z 为目标到坐标原点的距离。
当规定入射波和散射波的极化以及传播方向后,入射波 E i 与空间任意点 P 的目标散射波场强 E s 之间的关系是一维的线性系统关系。如果目标姿态角不变,则系统是时不变的,因此可以将目标看成一个时不变线性网络,其特性可用网络的冲激响应 h ( t )来表征。
当用入射平面波 E i ( t )= δ ( t )(Dirac-函数)照射一个有限尺寸目标时,其回波就是目标冲激响应 h ( t ),它具有如下特性:
(1)当目标处于 x y 平面后半空间时,且 t < 0,则 h ( t )=0;
(2)当
t
−
r
/
c
为大数值时,
h
(
t
)按指数律随时间衰落,这里
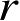 是坐标原点到观察点
P
的距离;
是坐标原点到观察点
P
的距离;
(3)当远距离,即 r ≫ L (目标最大尺寸)时,对散射场的横向分量,在给定的散射方向上, h ( t )随 r 按 r −1 f ( t − r / c )的形式变化。
用归一化 h I ( t )表示为
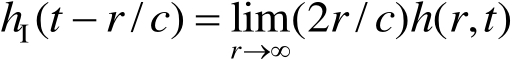
(2.12)
式中, h ( r , t )为 T −1 因次,归一化后 h I ( t − r / c )的量纲为无因次。
当入射平面波为任意波形 E i ( t )时,它与目标冲激响应的卷积给出目标输出散射场强 E s 为
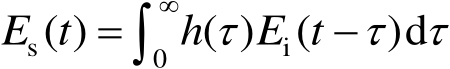
(2.13)
如图2.2所示。
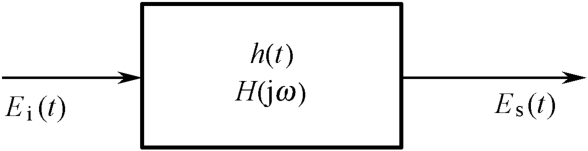
图2.2 目标的冲激响应和传递函数
由信号分析理论可知,任意瞬态响应波形可以用正弦波的谐波合成来表达,故也可在频率域定义远场区入射和散射场的关系,即
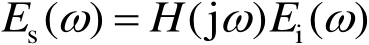
(2.14)
式(2.14)中,频域传递函数
H
(j
ω
)与时域冲激响应函数
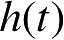 构成傅里叶变换对,即
构成傅里叶变换对,即
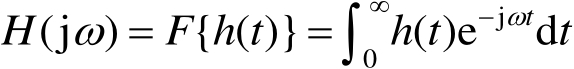
(2.15a)
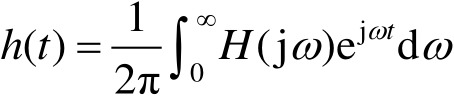
(2.15b)
由式(2.12)可得归一化频域传递函数 H I (j ω )与频域传递函数 H (j ω )的关系为
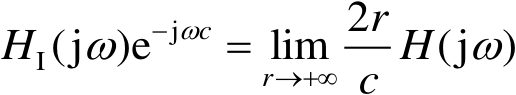
(2.16)
因此,可用功率谱响应特性将RCS表征为
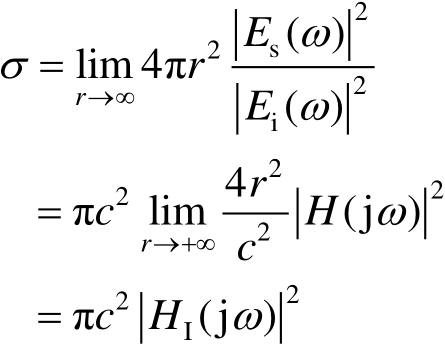
(2.17)
式(2.17)可作为目标宽带RCS的计算公式。 H I (j ω )的单位为s,所以 σ 的单位为m 2 。式(2.17)表明,宽带波照射下的目标RCS可用目标散射场的频域传递函数的平方来表征,亦即目标对功率的频率响应。
由宽带定义的RCS,它在频域上综合了目标对照射频率谱的响应,而在时域上它给出了目标沿视线方向上散射功率强度的分布,即目标散射中心的分布。
举一个完纯导电球的例子,如图2.3所示 [5] 。
在图2.3中,除图(a)外其他图均为包含不同谱的实测导电球的近似冲激响应,由扫频信号源产生照射波,接收回波经快速傅里叶变换而得。图2.3(b)与图2.3(c)中的高频振荡均是由于11.99GHz高频波截断点所致,而图2.3(b)与图2.3(c)之间差异则是由于带通时1GHz前的截断点所产生的低频波动,图2.3(d)与图2.3(e)是对图2.3(b)与图2.3(c)的谱幅度加窗后的响应,这里加的是凯泽-贝塞尔(Kairser-Bessel)窗,其窗函数表达式为
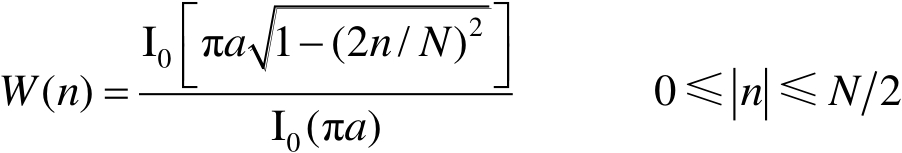
(2.18)
式(2.18)中, I 0 为第一类零阶修正贝塞尔函数, a 为球半径。
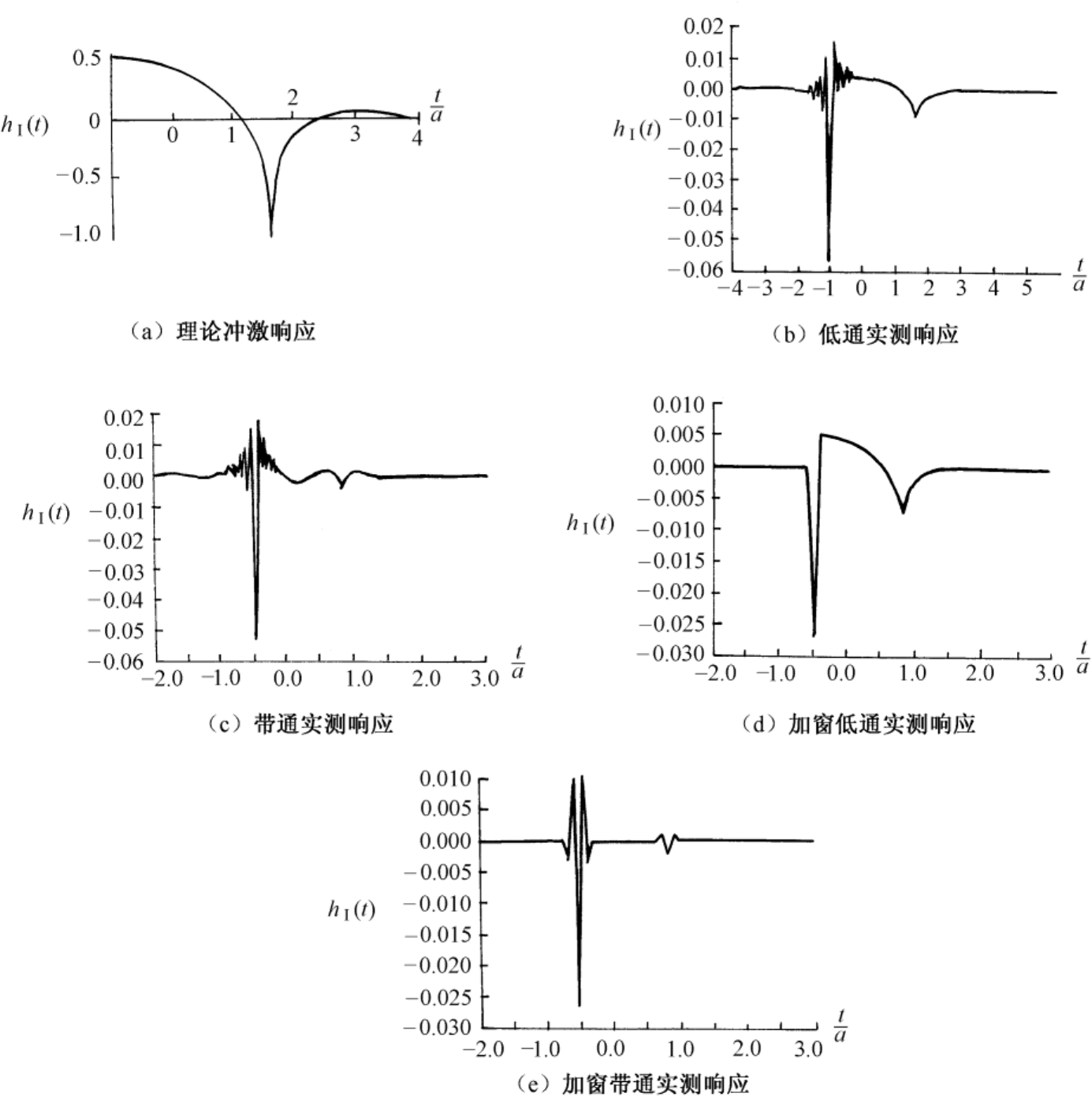
图2.3 完纯导电球的冲激响应
在主波瓣宽度相同情况下,凯泽-贝塞尔窗的旁瓣要低于汉宁(Hanning)窗。
导电球冲激响应曲线解释如下:它包含一个有限镜面反射回波和一个蠕动波回波。镜面反射响应由一个很大的负尖峰脉冲与紧接着的一个正阶跃所组成,其高频解析式可表示为伦伯格-克兰(Luneburg-Kline)展开式 [5]
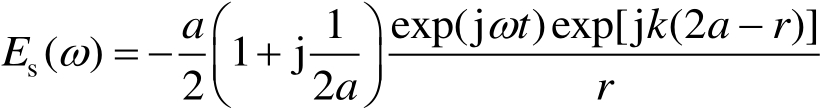
(2.19)
其时域表达式为
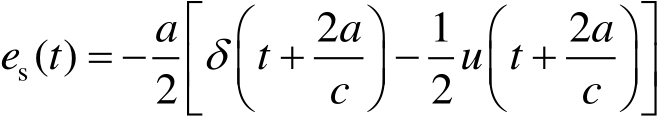
(2.20)
式(2.20)中,第一项为冲激脉冲,第二项为阶跃回波,其冲激高度正比于谱的宽度。图2.3中曲线的横坐标是以球半径
a
归一化后的时间轴,相位基准点(即
 )位于球心,因此镜面反射回波出现在
)位于球心,因此镜面反射回波出现在
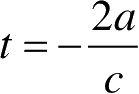 处,归一化后的时间轴出现在
处,归一化后的时间轴出现在
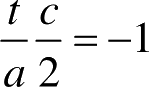 处(1ns的双程传播为15cm,正好是球直径)。从镜面反射点开始经过一个半径长的距离传播后,电磁波沿球阴影边界面绕球表面蠕动,如图2.4所示,最后蠕动波返回雷达接收端,该蠕动波距冲激脉冲的暂态位置应为
处(1ns的双程传播为15cm,正好是球直径)。从镜面反射点开始经过一个半径长的距离传播后,电磁波沿球阴影边界面绕球表面蠕动,如图2.4所示,最后蠕动波返回雷达接收端,该蠕动波距冲激脉冲的暂态位置应为
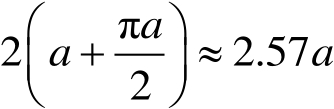
(2.21)
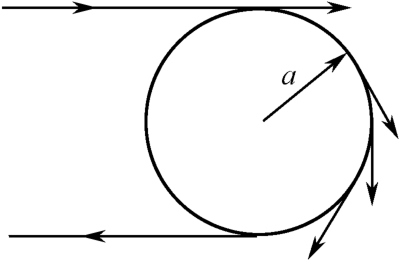
图2.4 导电球蠕动波传播途径
蠕动波传播时沿表面不断散发能量,频率愈高,相对电长度愈长,能量散发愈多,蠕动波衰减愈快。当
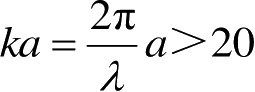 时,蠕动波几乎全部被衰减,导电球这时的RCS值几乎不随频率而变化。
时,蠕动波几乎全部被衰减,导电球这时的RCS值几乎不随频率而变化。
RCS的分类方法有多种。例如,按场区来分,有远场RCS与近场RCS,后者是距离的函数;按入射波频谱来分,有点频RCS与宽带RCS(这些已在上两节中涉及);按雷达站接收、发射位置来分,有单站RCS、准单站RCS与双站RCS。如图2.5所示,在目标坐标系中,以
θ
i
,
ϕ
i
代表入射波方向,
θ
s
,
ϕ
s
代表散射接收方向,当
θ
i
=
θ
s
,
ϕ
i
=
ϕ
s
时称单站(也称单基地)散射,也称后向散射;如果收/发不用同一天线,但相互很靠近,如
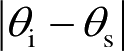 与|
ϕ
i
−
ϕ
s
| 均在5° 以内,则称为准单站散射;当收与发分得很开时,称为双站(即双基地)散射,也称非后向散射,发射入射波与接收散射波之间在目标坐标系中的夹角称为双站角5°(双基地角)。
与|
ϕ
i
−
ϕ
s
| 均在5° 以内,则称为准单站散射;当收与发分得很开时,称为双站(即双基地)散射,也称非后向散射,发射入射波与接收散射波之间在目标坐标系中的夹角称为双站角5°(双基地角)。
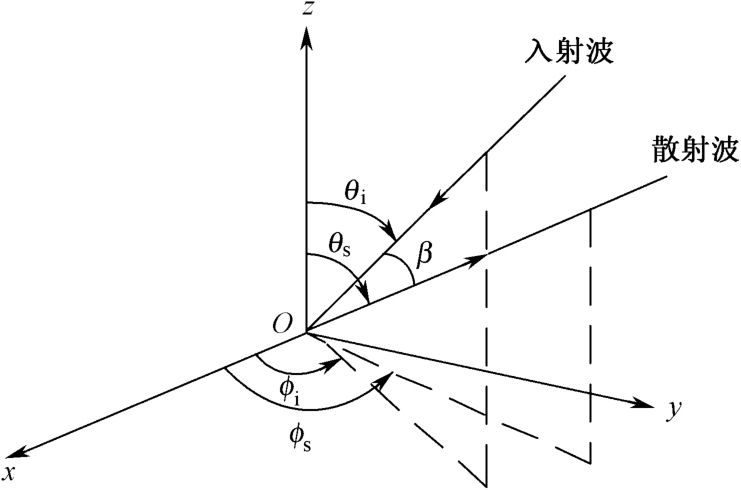
图2.5 双站RCS的表示
波长对目标RCS值的影响很大,因此下面重点叙述按波长对RCS分类的方法。
引入一个表征由波长归一化的目标特征尺寸大小的参数,称为 ka 值,即
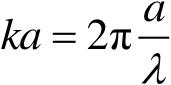
(2.22)
式(2.22)中,
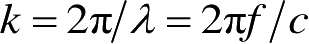 称为波数;
a
是目标的特征尺寸,通常取目标垂直于雷达视线横截面中的最大尺寸的一半。例如,对球目标,则取球半径为
a
;对锥体与柱目标,则取底部或柱截面半径为
a
。以
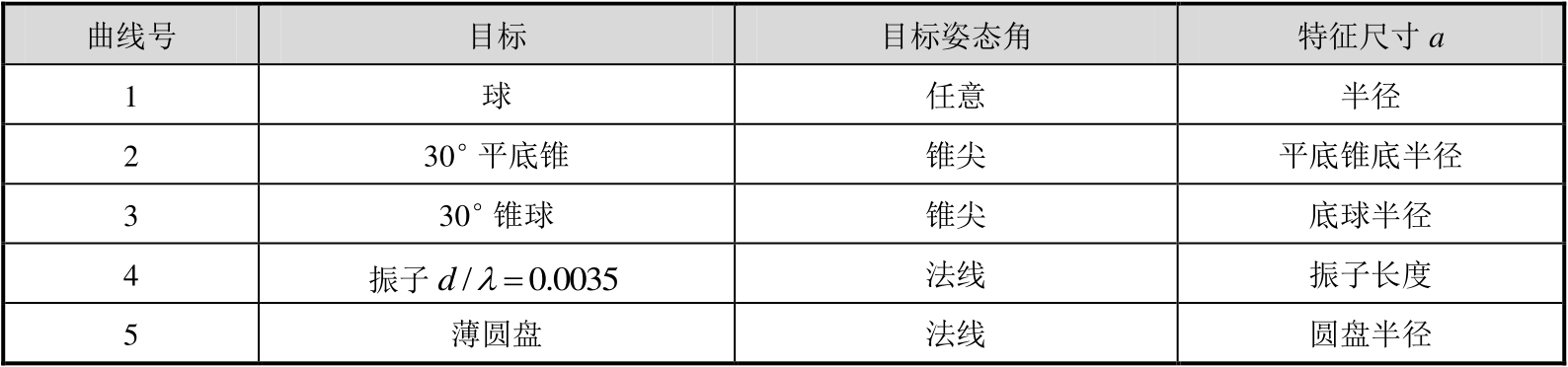
ka
变化为横坐标,几种形状的完纯导电目标的归一化RCS的比较如图2.6所示。各种目标的特征尺寸
a
如表2.1所示。该图中球目标为理论值,其他目标均为实验值。球的RCS与垂直入射下薄圆盘的RCS有很大差别,所以当
k
a
≤1 时,除振子目标外,其他目标的RCS相差不到4dB,因此按目标后向电磁散射特性的不同,将
ka
分为三个区域:瑞利区、谐振区和光学区。
称为波数;
a
是目标的特征尺寸,通常取目标垂直于雷达视线横截面中的最大尺寸的一半。例如,对球目标,则取球半径为
a
;对锥体与柱目标,则取底部或柱截面半径为
a
。以
ka
变化为横坐标,几种形状的完纯导电目标的归一化RCS的比较如图2.6所示。各种目标的特征尺寸
a
如表2.1所示。该图中球目标为理论值,其他目标均为实验值。球的RCS与垂直入射下薄圆盘的RCS有很大差别,所以当
k
a
≤1 时,除振子目标外,其他目标的RCS相差不到4dB,因此按目标后向电磁散射特性的不同,将
ka
分为三个区域:瑞利区、谐振区和光学区。
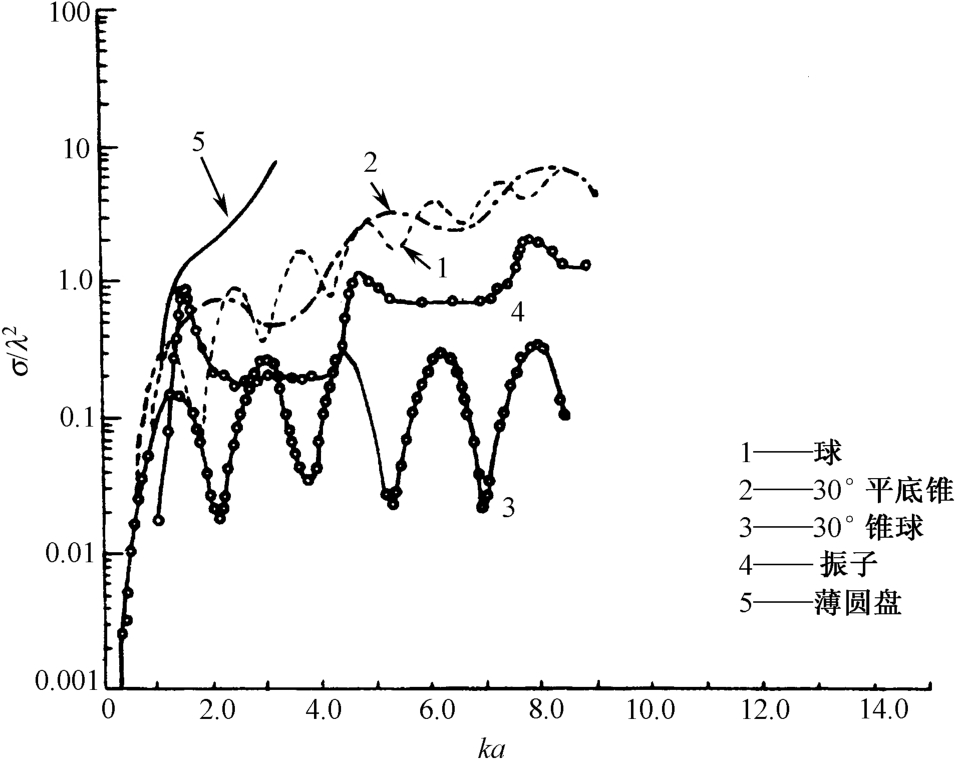
图2.6 几种形状的完纯导电目标的归一化RCS的比较 [6]
表2.1 几种形状目标的特征尺寸 a
1)瑞利区
瑞利区的特点是工作波长大于目标特征尺寸,一般取
 的范围。在这个区域内,RCS一般与波长的4次方成反比。对旋转物体的RCS,当沿旋转轴方向观测时的一般方程式为
的范围。在这个区域内,RCS一般与波长的4次方成反比。对旋转物体的RCS,当沿旋转轴方向观测时的一般方程式为
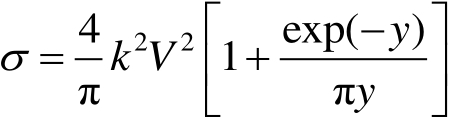
(2.23)
式(2.23)中, k =2π/ λ 为波数; V 为目标的体积; y 为形状指数,一个系数乘上目标的长宽比。
目标长度与传播方向目标最大尺寸相联系,其宽度与传播方向目标最大尺寸有关。表2.2给出了几种典型目标的体积和形状指数 y 的近似计算公式。
表2.2 几种典型目标的体积和形状指数 [6]
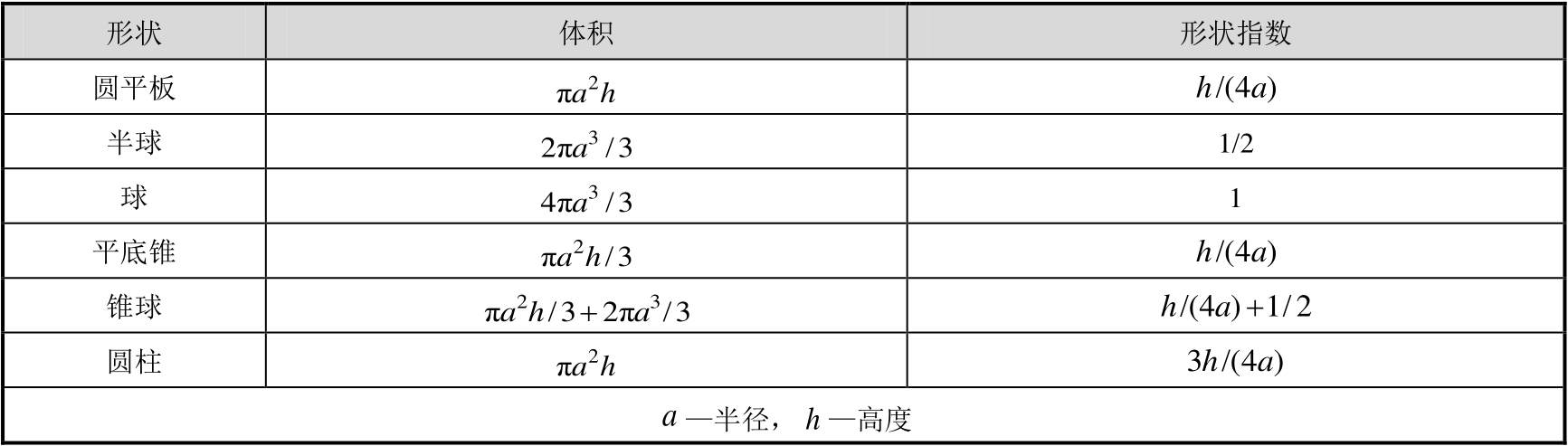
应该指出,对于像再入飞行器一类物体, y 总是大于1。因此,式(2.23)中括弧内的指数项可以忽略,所以,在瑞利区目标RCS的决定因素是波长归一化的物体体积。
如果观测的方向不是沿对称轴,而是沿其他方向,这些物体的RCS大都会下降。在偏离轴线的小角度方向上,这种变化缓慢,在多数姿态角内,由式(2.23)算出的RCS误差不会超过几分贝。
2)谐振区
谐振区的 ka 值一般在0.5≤ k a ≤20 范围内。在这个范围内,由于各个散射分量之间的干涉,RCS随频率变化产生振荡性的起伏,RCS的近似计算非常困难,一些简单形状物体可以参考如图2.6所示的数值。由该图可见,给定目标归一化RCS的值( σ / λ 2 )预计在10dB范围内起伏。在典型谐振区,当垂直于传播方向的物体尺寸近似为半波长整数倍时,RCS呈最小值,对锥球类尤为正确。对半锥角10° ~ 40° 范围的锥体,其最小RCS约0.01 λ 2 ,最大RCS约0.4 λ 2 ,平均RCS约为0.2 λ 2 。
严格地求解谐振区的散射场,需要有矢量波动方程的严格解或良好的近似解,一般飞机与导弹目标的计算是很复杂的,因此仍主要靠测量来求得。由于RCS随目标姿态角与频率变化迅速,会产生许多尖峰和深谷,因此读者需非常小心,有时仅在几度姿态角内进行统计平均,也会丢掉大起伏的信息。
谐振区的上界为光学区,二者之间的界限是不明确的。对球体,
k
a
=20;对飞机类目标,
 ,有时可达30以上。
,有时可达30以上。
3)光学区(又称高频区)
光学区的
ka
值一般取
 。目标RCS主要取决于其形状和表面粗糙度。目标外形的不连续导致RCS值的增大。对于光滑凸形导电目标,其RCS常近似为雷达视线方向的轮廓截面。然而当目标含有棱边、拐角、凹腔或介质等情况时,再用轮廓截面的概念是不正确的,图2.6中平底锥与锥球的RCS差别就说明这一点,由于平底锥的锥体与底部间连续区的不连续性使RCS显著增大。
。目标RCS主要取决于其形状和表面粗糙度。目标外形的不连续导致RCS值的增大。对于光滑凸形导电目标,其RCS常近似为雷达视线方向的轮廓截面。然而当目标含有棱边、拐角、凹腔或介质等情况时,再用轮廓截面的概念是不正确的,图2.6中平底锥与锥球的RCS差别就说明这一点,由于平底锥的锥体与底部间连续区的不连续性使RCS显著增大。
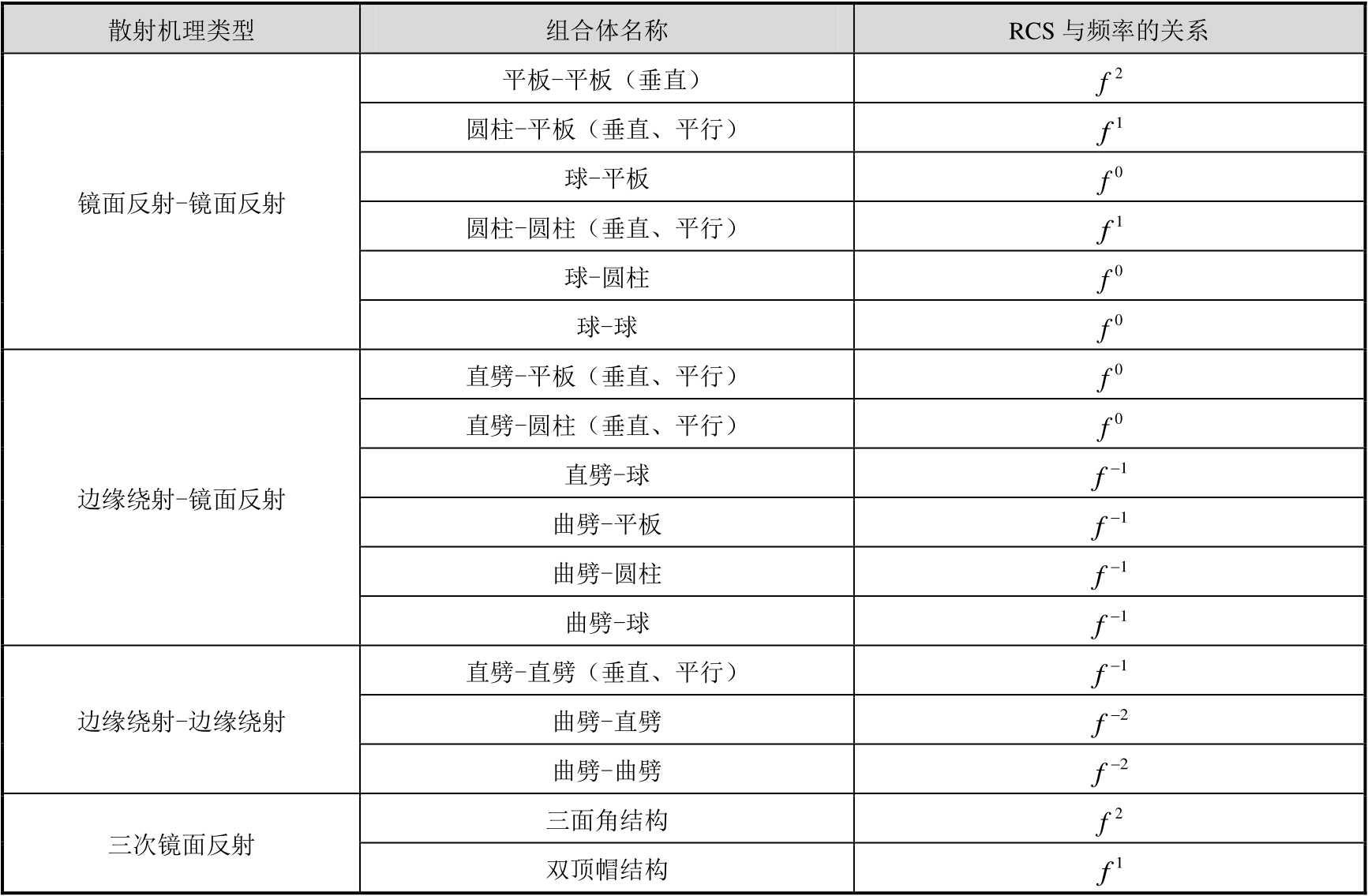
表2.3给出了光学区典型散射结构RCS与频率的关系。
表2.3 光学区典型散射结构RCS与频率的关系
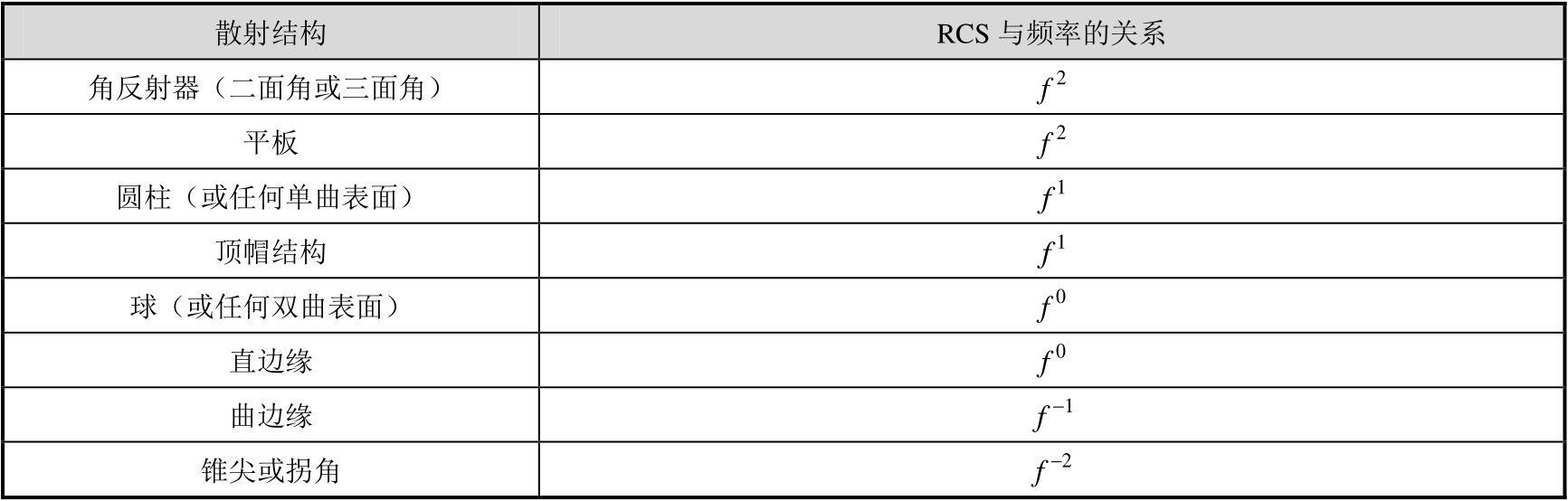
从表2.3可以看出,各典型散射结构RCS与频率的关系满足幂函数关系,且指数为整数,除角反射器和顶帽结构外,都是非耦合(单次)散射结构。可是,实际目标中还可能存在具有多次反射/绕射贡献的耦合散射结构,针对这些结构,上述幂函数关系仍然成立。
可以证明 [7] ,任意多次反射/绕射机理贡献的频率依赖关系如下式所示,即
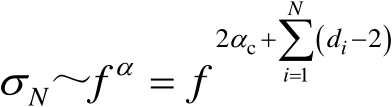
(2.24)
式(2.24)中,
α
为频率依赖因子;
N
为多次散射机理的散射次数;
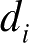 为反射几何元素的维数,对面、边缘和尖顶/角三种情形,分别为2、1和0;
α
c
为焦散修正因子,对无焦散、一重焦散和二重焦散三种情形,分别为0、0.5和1。
为反射几何元素的维数,对面、边缘和尖顶/角三种情形,分别为2、1和0;
α
c
为焦散修正因子,对无焦散、一重焦散和二重焦散三种情形,分别为0、0.5和1。
基于式(2.24),可以得到任意多次反射/绕射耦合结构的RCS频率关系。表2.4列举了若干典型二次、三次反射/绕射耦合结构RCS与频率的关系。
表2.4 典型二次、三次反射/绕射耦合结构RCS与频率的关系
研究单、双站RCS之间的等效关系有明显的理论价值和实际应用 [8] 。例如,对电磁散射的理论研究者来说,当通过数值法(如矩量法)求解RCS时,计算双站RCS要比计算单站RCS节省很多时间,因此,如果能利用双站RCS来计算单站RCS,无疑是很有价值的。而对雷达设计者来说,往往也试图通过单站RCS了解双站RCS的规律。
当目标被频率为
f
、电场矢量为
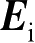 的平面波照射时,其双站RCS可用散射电场
E
s
表示为
的平面波照射时,其双站RCS可用散射电场
E
s
表示为
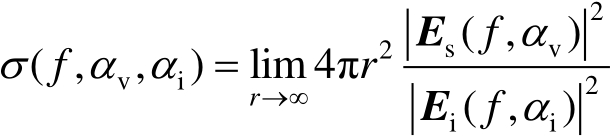
(2.25)
式(2.25)中,
α
i
是入射角;
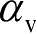 是观察角。利用单个散射中心的二次辐射波瓣方向图的概念,Kell
[9]
指出,双站RCS可以用在双站角的平分线处和在实际频率的
是观察角。利用单个散射中心的二次辐射波瓣方向图的概念,Kell
[9]
指出,双站RCS可以用在双站角的平分线处和在实际频率的
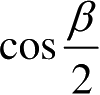 倍处测量的单站RCS来近似,即
倍处测量的单站RCS来近似,即
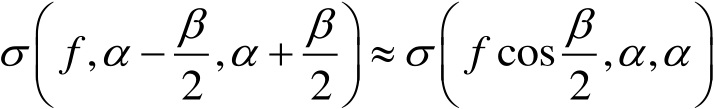
(2.26)
下面需要找出
β
必须多小才能在频率
f
和
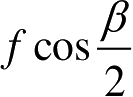 处给出相近的RCS。对长度为
L
的目标,在频率
f
处入射场和散射场之间最大的相位迟延
处给出相近的RCS。对长度为
L
的目标,在频率
f
处入射场和散射场之间最大的相位迟延
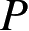 为
为
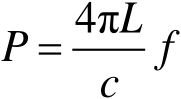
(2.27)
式(2.27)中,
c
是光速,
L
为目标长度,
f
为频率,且考虑了双程。如果在频率
f
和
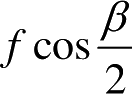 之间最大相差为Δ
P
,则
之间最大相差为Δ
P
,则
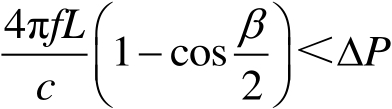
(2.28)
利用
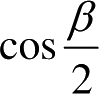 的小宗量近似,得
的小宗量近似,得
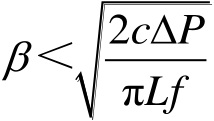
(2.29)
如果选择Δ
P
=11°,则
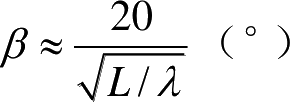 。例如,对
L
/
λ
为4和16,
。例如,对
L
/
λ
为4和16,
 应分别为10°和5°。如果满足式(2.29),则可用双站RCS来近似单站RCS,即
应分别为10°和5°。如果满足式(2.29),则可用双站RCS来近似单站RCS,即
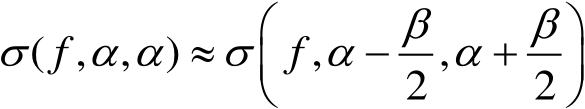
(2.30)
式(2.30)表明,当双站角不大时,双站RCS与位于发射和接收方向之间的双站角平分线处的单站RCS相同。这与Crispin等人 [10] 提出的基于物理光学近似的单-双站等效定理是一致的。可以推断,如果收/发位置互换的话,RCS不变。
文献[11]还给出了一个由目标单站RCS快速计算其双站RCS的经验公式,将双站RCS表示为目标的单站RCS和双站角的函数,即
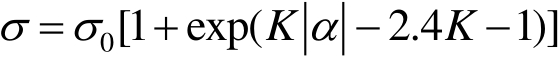
(2.31)
式(2.31)中,
σ
0
是目标的单站RCS(以m
2
为单位);
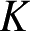 是由目标结构和复杂程度确定的经验系数;
α
是双站角(以弧度为单位),且
是由目标结构和复杂程度确定的经验系数;
α
是双站角(以弧度为单位),且
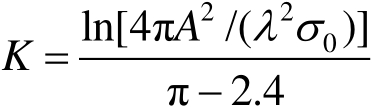
这里, A 为在垂直于雷达波束方向上投影的目标面积, λ 为波长。
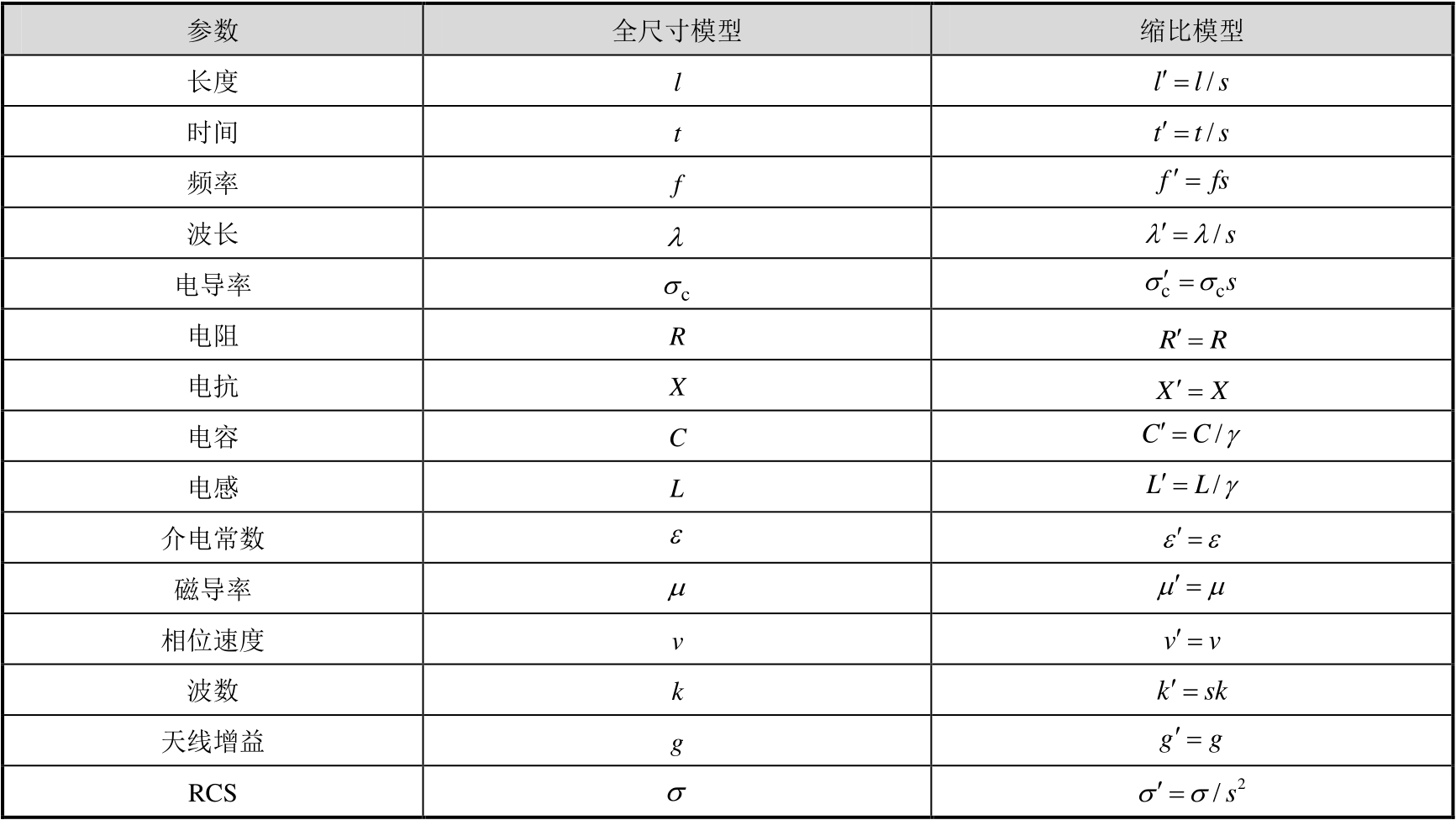
在室内散射测量中,受暗室尺寸、全尺寸目标加工成本等因素的限制,绝大多数暗室常用于缩比目标模型的测量,为此必须找出全尺寸目标与目标缩比模型之间应满足的电磁关系,即确定目标尺寸、系统时间尺度(工作频率)、电磁场强度、材料参数等物理量在什么样的条件下,能够实现系统的精确缩比,以便对模型制造和测量提出要求,开展实验,再由模型实验结果推出原型结果。本节从麦克斯韦(Maxwell)方程出发,针对一般性目标推导电磁缩比关系 [12] ,然后退化到理想导体情况,讨论材料目标缩比关系复杂化的问题。
实际(原型)系统中的电磁场由下面的方程描述,即
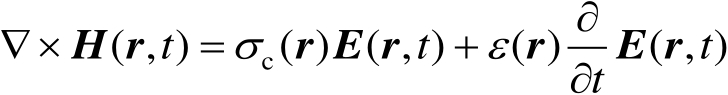
(2.32)
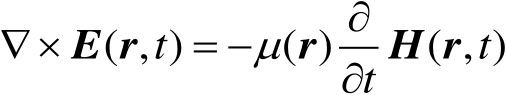
(2.33)
式中, E 和 H 分别为电场强度矢量和磁场强度矢量; ε , μ , σ c 分别为介电常数、磁导率和电导率; r , t 分别为位置矢量和时间。
缩比(模型)系统中的电磁场与式(2.32)和式(2.33)类似,只是相关量用带撇的符号表示如下
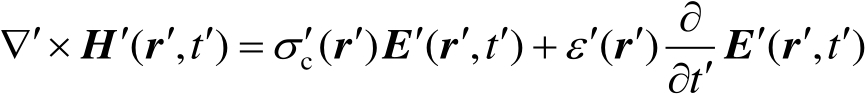
(2.34)
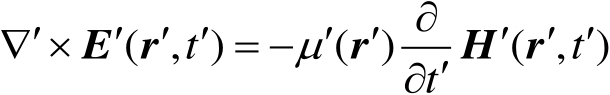
(2.35)
在笛卡儿坐标系下,假定实际系统和缩比系统的坐标对应关系为
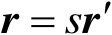
(2.36)
式(2.36)中, s 定义为尺寸缩比因子。式(2.36)所施加的条件代表了目标尺寸缩比的要求,即在相同量纲下,坐标系统 x , y , z 中的各点按因子 s 缩比到对应的 x ′, y ′, z ′系统。要进行精确缩比,还需考虑如下条件,即
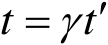
(2.37)
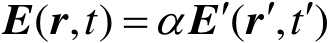
(2.38)
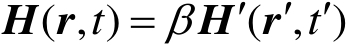
(2.39)
式中,
γ
,
α
,
β
分别为时间、电场强度和磁场强度的缩比因子。四个缩比因子
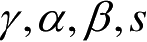 都是必须的,因为它们能够量化包括质量、长度、时间和电荷在内的任何电磁场参数。已知这四个缩比因子,就能确定实际系统和缩比系统中的电磁场参数关系,当然还必须满足麦克斯韦方程。
都是必须的,因为它们能够量化包括质量、长度、时间和电荷在内的任何电磁场参数。已知这四个缩比因子,就能确定实际系统和缩比系统中的电磁场参数关系,当然还必须满足麦克斯韦方程。
将式(2.37)~式(2.39)代入式(2.34)和式(2.35)中,且由式(2.36)和式(2.37)可知,∇′=
s
∇,
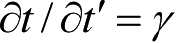 ,于是,可将缩比系统中的麦克斯韦方程变换为
,于是,可将缩比系统中的麦克斯韦方程变换为
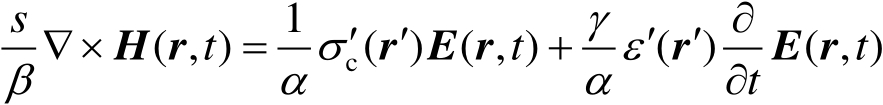
(2.40)
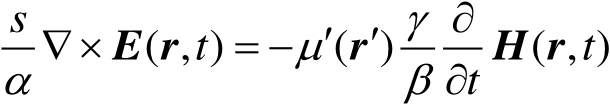
(2.41)
为实现这两个系统的严格等效,式(2.40)和式(2.41)必须与式(2.32)和式(2.33)相同,因此有
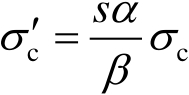
(2.42)
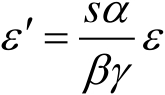
(2.43)
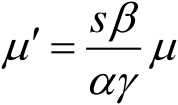
(2.44)
以上三个关系式即为精确缩比时材料需要满足的条件。由式(2.36)~式(2.39)、式(2.42)~式(2.44),根据有关参量的定义,可以导出所有电磁物理参量的相似关系 [12] ,表2.5给出了与RCS测量有关的一些参量的绝对缩比条件。
表2.5 与RCS测量有关的一些参量的绝对缩比条件
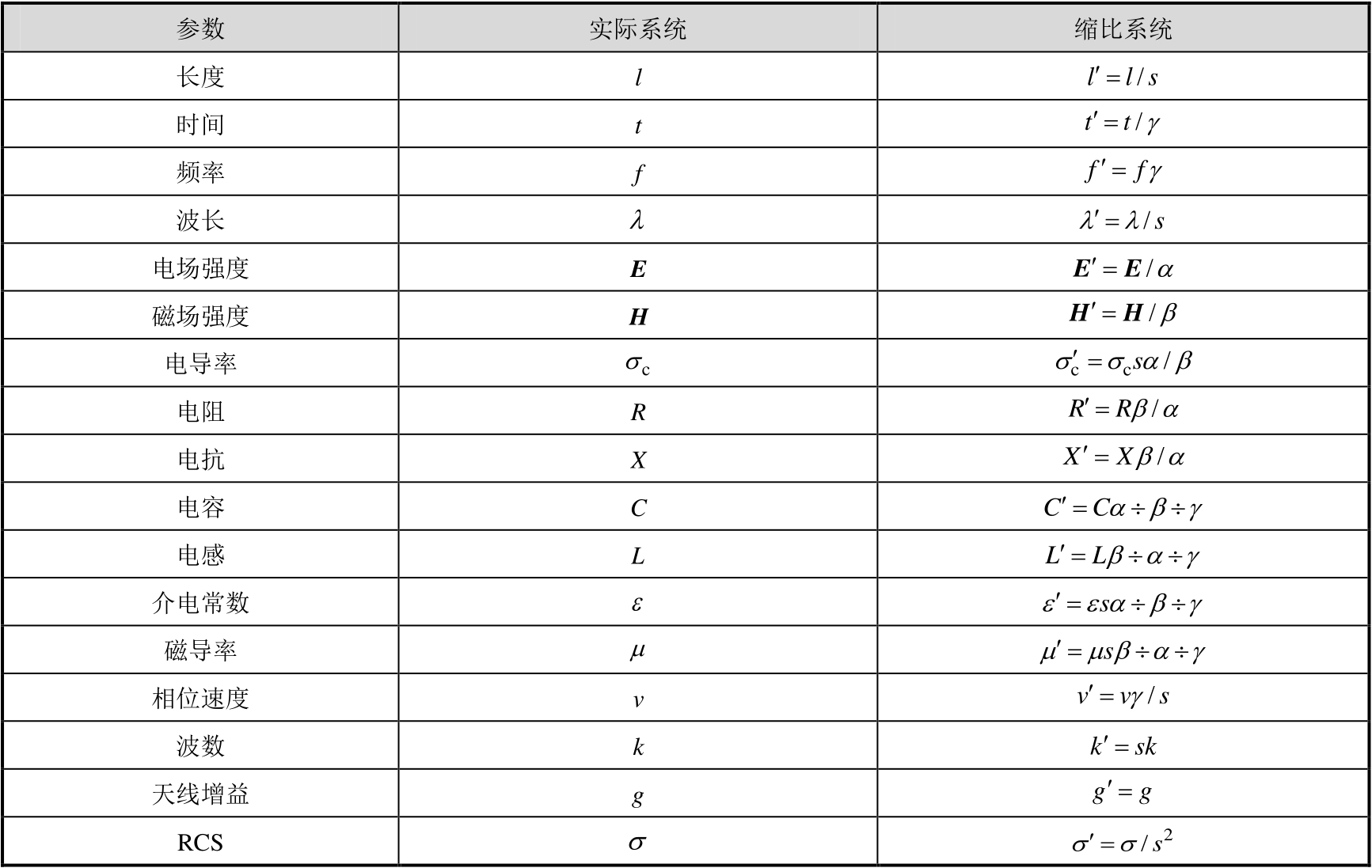
理论上,只要满足绝对缩比条件,缩比因子可以任意选取,但在实际问题中总是存在一些限制条件。就RCS缩比测量而言,由于测量通常是在空气(可以近似看成自由空间)中进行的,而在自由空间中要求
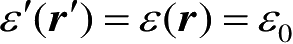 ,
μ
′(
r
′)=
μ
(
r
)=
μ
0
,于是由式(2.43)和式(2.44)可得
,
μ
′(
r
′)=
μ
(
r
)=
μ
0
,于是由式(2.43)和式(2.44)可得
α = β
(2.45)
s = γ
(2.46)
上述条件需要电导率满足以下关系,即
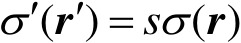
(2.47)
因此,对于实际系统,只有 α 和 s 两个参数能被任意选取。通常电导率相似变换式(2.47)限制的条件并不需要严格满足,因为若实际模型和缩比模型都在空气中,尽管空气的电导率会随频率变化,但空气电导率非常小,基本可以当成绝缘体,因此由电导率导致的误差非常小。当然,除了在空气中,式(2.45)~式(2.47)在目标中也是需要满足限制条件才行。
由式(2.45)~式(2.47)和表2.5,可得RCS测量时全尺寸目标与缩比目标模型的电磁缩比关系如表2.6所示。
表2.6 全尺寸目标与缩比目标模型的电磁缩比关系
根据表2.6,1: s 缩比模型的RCS( σ ′)与折算成1:1真实尺寸时目标的RCS( σ )有如下关系
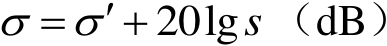
而缩比模型的测试频率 f ′应为实际目标测试频率 f 的 s 倍。
对于理想导体( σ , σ ′→ ∞ )目标,式(2.47)是必然成立的,并且考虑到电磁波无法进入目标内部,目标自身的 ε 和 μ 的取值对缩比问题没有实际影响,而目标外部空气是可以满足介电常数和磁导率不变的要求的。因此,理想导体目标能满足表2.6所示所有电磁量的缩比关系,这些关系可以由尺寸缩比系数 s 唯一确定。
对于无导电损耗介质( σ , σ ′→0)目标,式(2.47)同样成立。因此,理论上只要满足介电常数与磁导率不变,它与理想导体一样,能够满足所有电磁量(包括RCS)的缩比关系。但考虑到缩比频率与原始频率并不相等,而是满足 f ′= s f 的关系,若要求介电常数在缩比频率和原始频率上保持不变,而原型目标上采用的材料(如吸波材料)通常是色散的,不同频率下介电常数是变化的,这就要求缩比模型中必须采用不同的材料以保证介电常数不变的要求。可是,在实际情况中制作一种具有指定介电常数的材料还是比较困难的。
对于具有导电损耗的介质目标,
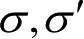 是非零有限值,缩比模型的电导率与实际目标的电导率之间必须严格满足式(2.47),这在实际情况中也是难以实现的,极大地限制了包含复合吸波材料之类的低散射目标的缩比测量,因此一直是目标电磁散射特性研究的一个难点问题
[13]
。对此,有学者从其他角度出发探讨有耗介质目标电磁缩比关系近似得到满足的条件,如刘铁军等人
[14]
,提出了三个对有耗介质目标进行散射缩比测量时所应遵循的相似法则,只要满足其中一个相似法则,就可以将所测模型的RCS变换为原模型的RCS;时振栋等人
[15-16]
将目标等效成若干基本简单体的组合,然后基于由物理光学和驻相法获得的简单体散射的解析公式,给出了目标RCS随几何长度和频率变化的依赖公式,从而完成由缩比涂覆飞弹模型RCS测量数据向全尺寸目标RCS数据的推算。
是非零有限值,缩比模型的电导率与实际目标的电导率之间必须严格满足式(2.47),这在实际情况中也是难以实现的,极大地限制了包含复合吸波材料之类的低散射目标的缩比测量,因此一直是目标电磁散射特性研究的一个难点问题
[13]
。对此,有学者从其他角度出发探讨有耗介质目标电磁缩比关系近似得到满足的条件,如刘铁军等人
[14]
,提出了三个对有耗介质目标进行散射缩比测量时所应遵循的相似法则,只要满足其中一个相似法则,就可以将所测模型的RCS变换为原模型的RCS;时振栋等人
[15-16]
将目标等效成若干基本简单体的组合,然后基于由物理光学和驻相法获得的简单体散射的解析公式,给出了目标RCS随几何长度和频率变化的依赖公式,从而完成由缩比涂覆飞弹模型RCS测量数据向全尺寸目标RCS数据的推算。