效能衡量指标(Performance Metrics)是定义模型优劣的衡量标准,要了解各种效能衡量指标,先要理解混淆矩阵(Confusion Matrix),以二分类而言,如图4.14。
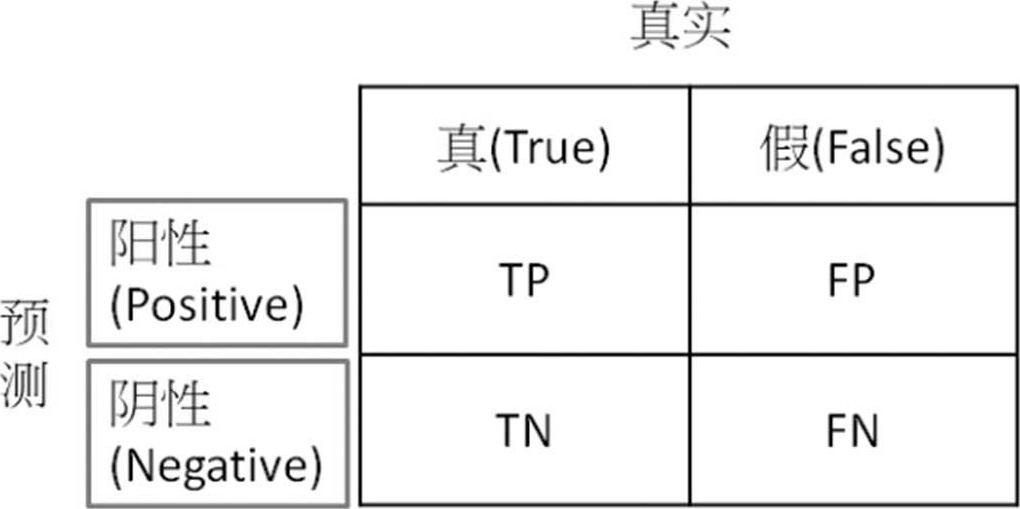
图4.14 混淆矩阵(Confusion Matrix)
(1)横轴为预测结果,分为阳性(Positive,简称P)、阴性(Negative,简称N)。
(2)纵轴为真实状况,分为真(True,简称T)、假(False,简称F)。
(3)依预测结果及真实状况的组合,共分为四种状况:
TP(真阳性):预测为阳性,且预测正确。
TN(真阴性):预测为阴性,且预测正确。
FP(伪阳性):预测为阳性,但预测错误,又称型一误差(Type I Error),或α误差。
FN(伪阴性):预测为阴性,但预测错误,又称型二误差(Type II Error),或β误差。
(4)有了TP/TN/FP/FN之后,我们就可以定义各种效能衡量指标,常见的有四种:
准确率(Accuracy)=(TP+TN)/(TP+FP+FN+TN),即预测正确数/总数。
精确率(Precision)=TP/(TP+FP),即正确预测阳性数/总阳性数。
召回率(Recall)=TP/(TP+FN),即正确预测阳性数/实际为真的总数。
F1=精确率与召回率的调和平均数,即1/[(1/Precision)+(1/Recall)]。
(5)FP(伪阳性)与FN(伪阴性)是相冲突的,以Covid-19检验为例,如果降低阳性认定值,可以尽最大可能找到所有的确诊者,减少伪阴性,避免传染病扩散,但有些没染疫的人因而被误判,伪阳性相对增加,导致资源的浪费,更严重的可能造成医疗体系崩溃,得不偿失。
(6)除了准确率之外,为什么还需要参考其他指标?
以医疗检验设备来举例,假设某疾病实际染病的比率为1%,这时我们拿一个故障的检验设备,不管有无染病,都判定为阴性,这时计算设备准确率,结果竟然是99%。会有这样离谱的统计,是因为在此案例中,验了100个样本,确实只错一个。所以,碰到真假比例悬殊的不平衡(Imbalanced)样本,必须使用其他指标来衡量效能。
精确率:再以医疗检验设备为例,我们只关心被验出来的阳性病患,有多少比例是真的染病,而不去关心验出为阴性者,因为验出为阴性,通常不会再被复检,或者不放心又跑到其他医院复检,医院其实很难追踪他们是否真的患病。
召回率:以Covid-19为例,我们关心的是所有的染病者有多少比例被验出阳性,因为一旦有漏网之鱼(伪阴性),可能就会造成小区传染。
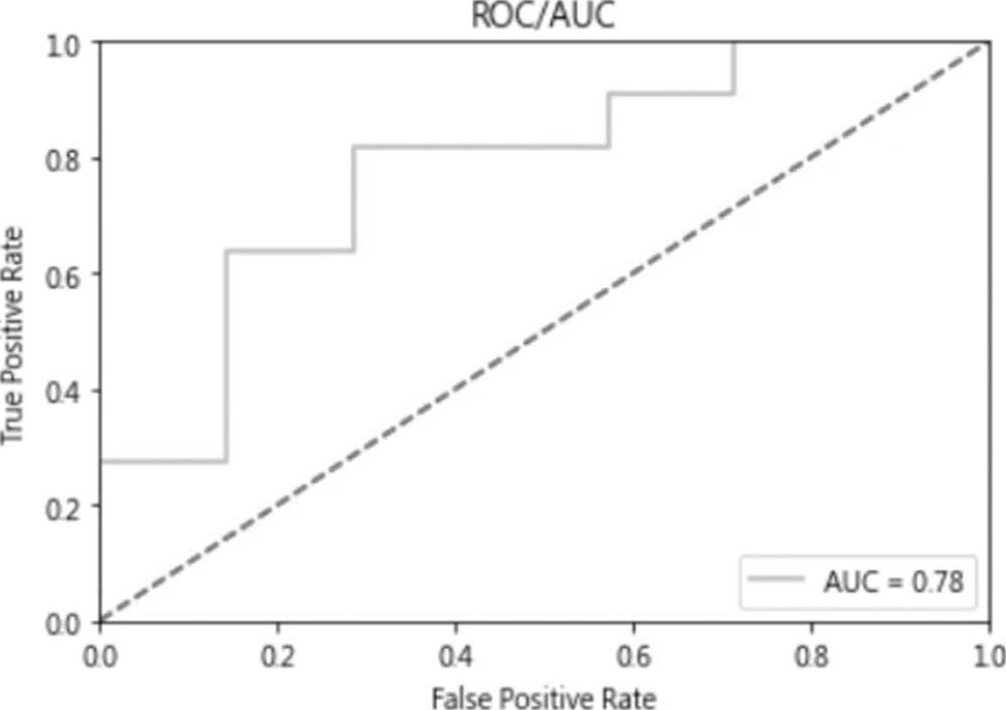
(7)针对二分类,还有一种较客观的指标称为ROC/AUC曲线,它是在各种检验门槛值下,以假阳率为 X 轴,真阳率为 Y 轴,绘制出来的曲线,称为ROC。覆盖的面积(AUC)越大,表示模型在各种门槛值下的平均效能越好,这个指标有别于一般预测固定以0.5当作判断真假的基准。
TensorFlow/Keras的效能衡量指标可参阅Keras官网 [22] ,但PyTorch不提供相关效能衡量指标的函数,可以使用NumPy或Scikit-Learn的函数,可参阅“Scikit-Learn文件” [23] ,如果要一律采用PyTorch相关的套件,有兴趣的读者可以参阅“TorchMetrics文件” [24] ,本文采用Scikit-Learn。
下列三个范例的程序代码请参考【04_15_效能衡量指标.ipynb】。
范例1.假设有8笔数据如下,请计算混淆矩阵(Confusion Matrix)。
实际值=[0, 0, 0, 1, 1, 1, 1, 1]
预测值=[0, 1, 0, 1, 0, 1, 0, 1]
(1)加载相关套件。

(2)Scikit-Learn提供混淆矩阵(Confusion Matrix)函数,程序代码如下。

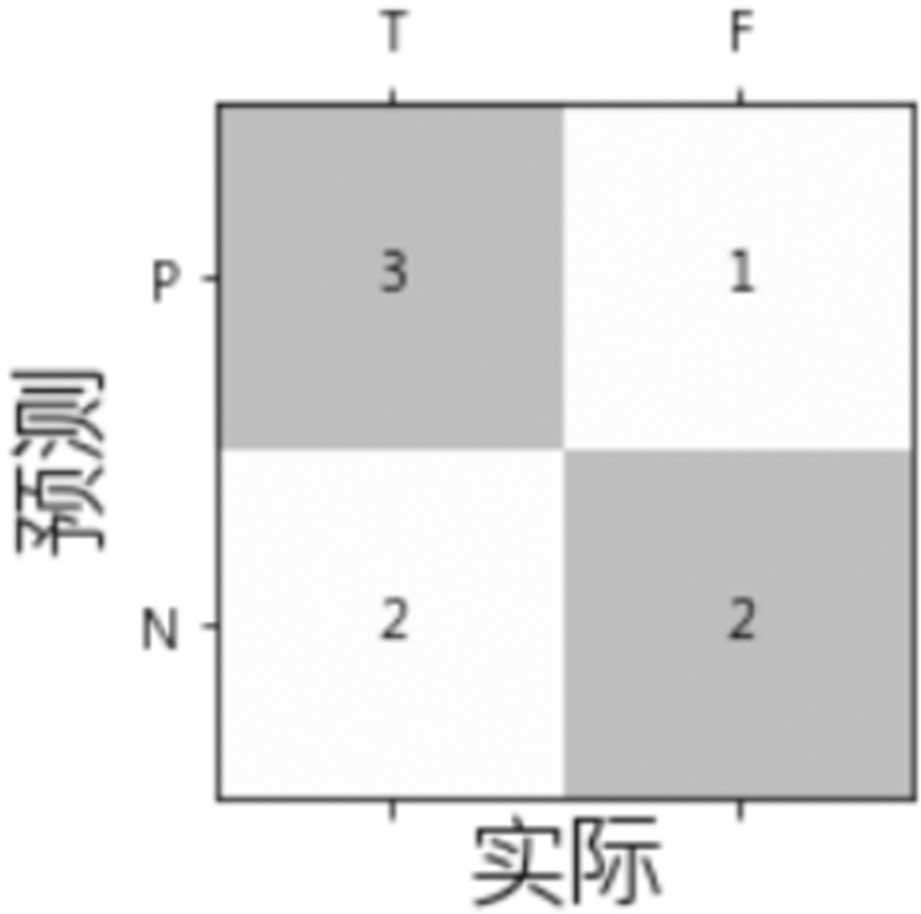
注意,Scikit-Learn提供的混淆矩阵,回传值与图4.14位置不同。
实际值与预测值上下比较,TP为(1, 1)、FP为(0, 1)、TN为(0, 0)、FN为(1, 0)。
执行结果:TP=3, FP=1, TN=2, FN=2。
(3)绘图。

执行结果。
范例2.按上述数据计算效能衡量指标。
(1)准确率。
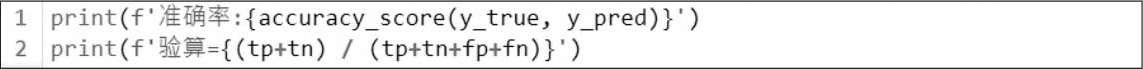
执行结果:0.625。
(2)计算精确率。

执行结果:0.75。
(3)计算召回率。

执行结果:0.6。
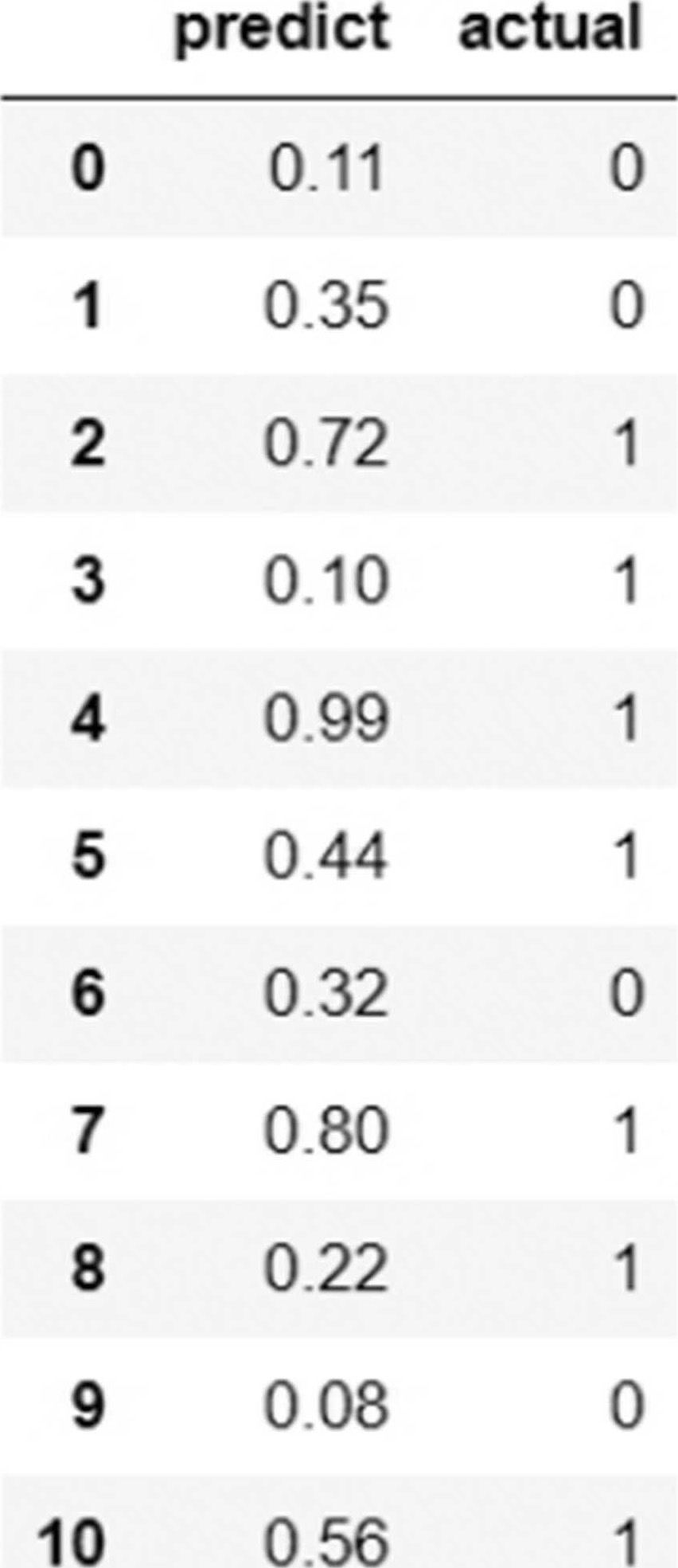
范例3.按数据文件data/auc_data.csv计算AUC。
(1)读取数据文件。

执行结果。
(2)以Scikit-Learn函数计算AUC。

执行结果。

(3)绘制AUC。

执行结果。